↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current disentanglement methods, while aiming for compositional representations, fundamentally rely on symbolic approaches that mismatch the continuous nature of deep learning. This mismatch hinders performance, as gradient flow is fragmented and the expressiveness of continuous vector spaces is not fully leveraged. This paper tackles this issue head-on.
The proposed solution is Soft Tensor Product Representations (Soft TPRs), which offer inherently continuous compositional representations. The paper introduces the Soft TPR Autoencoder, a novel architecture explicitly designed for learning Soft TPRs. Empirical results show that Soft TPRs offer advantages across multiple dimensions: state-of-the-art disentanglement, faster learner convergence, and superior downstream performance, especially in data-scarce scenarios.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in representation learning and AI because it directly addresses a critical challenge: the mismatch between the continuous nature of deep learning vector spaces and the symbolic treatment of compositional structure in existing methods. By proposing Soft TPR, the study offers a novel framework that promises more efficient and effective learning of compositional structures, impacting downstream model performance. This opens exciting new avenues in disentanglement, visual representation learning, and weakly supervised learning.
Visual Insights#
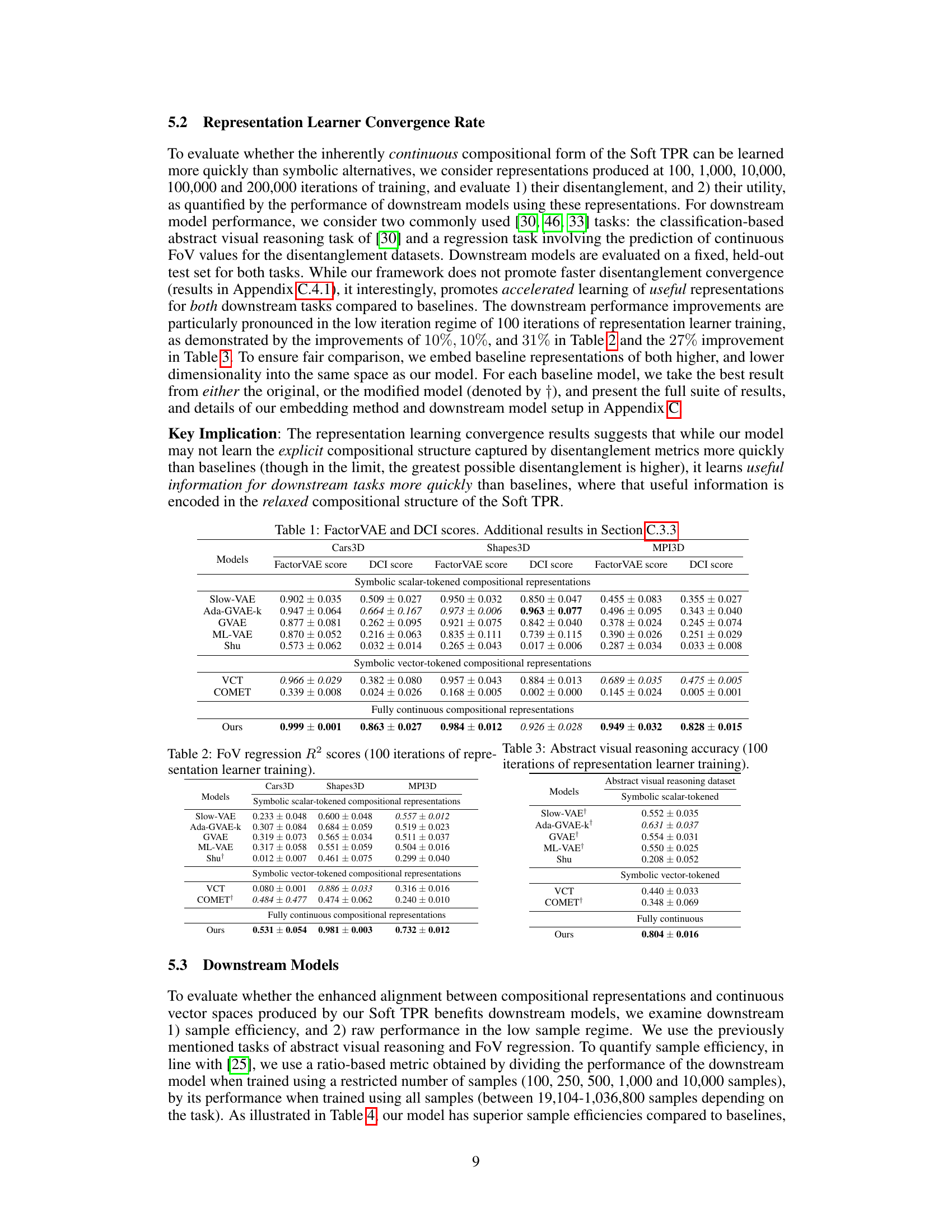
This figure illustrates the difference between symbolic and continuous compositional representations. (a) shows a symbolic representation where factors of variation (FoVs) are concatenated into distinct slots. (b) shows a continuous representation (TPR) where FoVs are superimposed, creating a continuous blend. (c) highlights that TPRs are limited to a discrete subset of points in the vector space, while Soft TPRs relax this constraint to encompass a continuous region, allowing for more flexibility in representation.
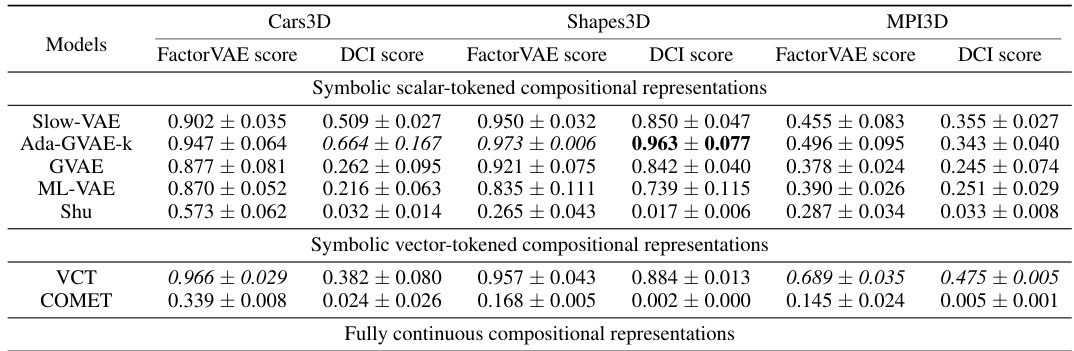
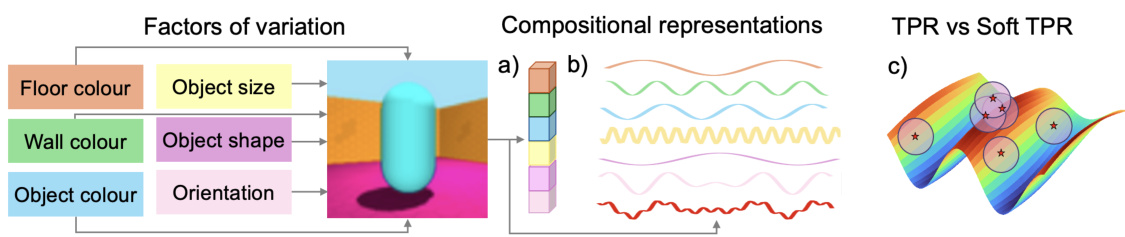
This table presents the FactorVAE and DCI disentanglement scores for different models on three datasets: Cars3D, Shapes3D, and MPI3D. The models are categorized into three groups: symbolic scalar-tokened compositional representations, symbolic vector-tokened compositional representations, and fully continuous compositional representations. The scores show the level of disentanglement achieved by each model, with higher scores indicating better disentanglement. The table highlights the superior performance of the Soft TPR Autoencoder in terms of disentanglement compared to the baseline models.
In-depth insights#
Continuous TPR#
The concept of “Continuous TPR” suggests a significant advancement in tensor product representations (TPRs) by addressing their inherent limitations. Traditional TPRs suffer from a discrete mapping, restricting their applicability to specific, formally structured domains. A continuous TPR, however, relaxes this constraint, enabling the representation of quasi-compositional structures and the modeling of real-world data, which are often only partially compositional. This approach seems particularly beneficial for deep learning frameworks that operate in continuous vector spaces, where the symbolic nature of standard TPRs can be incongruous. By creating a continuous version of the model, it is able to leverage the full expressivity of continuous vector spaces, overcoming issues with gradient propagation. The resulting model can capture richer interactions between constituent parts and may even enhance sample efficiency, particularly for downstream models.
Soft TPR Autoencoder#
The Soft TPR Autoencoder is a novel neural network architecture designed to learn Soft Tensor Product Representations (Soft TPRs). Its core innovation lies in its ability to seamlessly bridge the gap between the continuous nature of deep learning vector spaces and the compositional structure of data. Unlike traditional TPR methods, which enforce a strict, symbolic structure limiting their flexibility, the Soft TPR Autoencoder embraces continuous representations. This is achieved by relaxing the rigid mathematical constraints of TPRs, enabling the network to learn richer, more nuanced compositional structures. The architecture incorporates a weakly supervised approach, leveraging paired samples to guide disentanglement without the need for strong supervision. This makes it suitable for real-world scenarios where obtaining precise labels may be difficult. The Soft TPR Autoencoder’s design incorporates an encoder to map input data to a Soft TPR, a specially designed decoder to reconstruct the input from the Soft TPR, and a loss function that combines both unsupervised and weakly supervised components to ensure both a correct representational form and content.
Visual Composition#
Visual composition, in the context of computer vision research, refers to the process of understanding and representing how individual visual elements combine to form complex scenes. It’s a crucial aspect of scene understanding, mirroring how humans perceive and interpret images. Effective visual composition models need to disentangle underlying factors of variation, such as object shape, color, and pose, while also capturing the relationships between these elements. Successful models often leverage techniques such as tensor product representations or deep learning architectures to achieve this complex task, but challenges remain in handling variations, ambiguities, and the sheer complexity of real-world visual data. The ultimate goal is to build systems capable of not only recognizing objects within images but also understanding the composition and arrangement of those objects, allowing for more robust and meaningful scene interpretation.
Disentanglement#
Disentanglement, in the context of representation learning, centers on creating models capable of separating distinct, underlying factors of variation within data. This is crucial for achieving interpretable and robust AI systems. The paper highlights the inherent tension between disentanglement’s symbolic nature (treating representations as concatenations of features) and the continuous vector spaces employed by deep learning. This mismatch leads to suboptimal performance, motivating the proposal of a continuous framework. The authors argue that existing methods create a symbolic-continuous mismatch by using a fundamentally symbolic treatment of compositional structure, which doesn’t align with the continuous vector spaces in deep learning. The limitation of existing disentanglement approaches is addressed by a new type of continuous representation. Achieving true disentanglement is a challenging task, especially in unsupervised or weakly supervised settings. The paper’s emphasis on the continuous aspect to resolve the symbolic-continuous mismatch and its implications for downstream model performance is a significant contribution.
Future of TPRs#
The future of Tensor Product Representations (TPRs) lies in addressing their current limitations while capitalizing on their strengths. Overcoming the restrictive algebraic structure is crucial; Soft TPRs represent a promising step towards more flexible and continuous representations, better suited for real-world data with quasi-compositional properties. Improving computational efficiency is also necessary; exploring tensor contraction techniques and efficient algorithms will enable scaling to larger datasets and more complex tasks. Furthermore, extending TPRs beyond formal domains like language and mathematics to incorporate visual and other modalities remains an important area of exploration. Combining TPRs with other deep learning architectures could lead to powerful hybrid models that leverage the representational benefits of TPRs with the strengths of other approaches. Finally, the development of new learning algorithms tailored to TPRs will further improve their effectiveness and applicability.
More visual insights#
More on figures

This figure compares three different types of compositional representations: (a) symbolic representation, where factors of variation (FoVs) are concatenated; (b) Tensor Product Representation (TPR), where FoVs are superimposed continuously; and (c) Soft TPR, a relaxed version of TPR that allows for a continuous range of representations around the original TPR points. The figure highlights the inherent continuous nature of Soft TPR and its advantage over symbolic and traditional TPR methods for deep learning.
This figure illustrates three different types of compositional representations: (a) symbolic, (b) TPR, and (c) Soft TPR. The symbolic representation uses discrete slots for each factor of variation (FoV), while the TPR and Soft TPR use a continuous superposition of FoVs. The Soft TPR is a relaxed version of the TPR, allowing for a wider range of continuous representations.
This figure shows three different types of compositional representations. (a) shows a symbolic representation where factors of variation (FoVs) are concatenated, like a string. (b) illustrates a continuous representation using tensor product representation (TPR), where FoVs are superimposed like waves. Finally, (c) compares TPR with Soft TPR, highlighting that Soft TPR relaxes the strict mathematical requirements of TPR while retaining its key properties, resulting in a larger and continuous space of valid representations.

This figure compares three different types of compositional representations: (a) symbolic, (b) TPR, and (c) Soft TPR. The symbolic representation uses discrete slots, the TPR is mathematically constrained, and the Soft TPR relaxes the TPR constraints for continuous representations. The figure visually illustrates the difference between the approaches with colored blocks for symbolic, waves for TPR, and translucent circles on a manifold to represent Soft TPR.
This figure compares different types of compositional representations. Panel (a) illustrates the traditional symbolic, discrete representation used in disentanglement methods. Panel (b) depicts the continuous, superimposed representation of the proposed Soft TPR. Panel (c) visually demonstrates how Soft TPR relaxes the stringent constraints of the original TPR by allowing for larger continuous regions of the representational space to represent compositional structure.
This figure illustrates three different types of compositional representations: (a) shows a symbolic representation where factors of variation (FoVs) are concatenated into distinct slots, (b) shows a continuous representation where FoVs are superimposed, and (c) compares the discrete TPR representation to the continuous Soft TPR representation. The Soft TPR relaxes the strict constraints of the TPR, allowing for a more flexible representation of compositional structure.

This figure compares and contrasts three different types of compositional representations. (a) shows a symbolic representation where factors of variation (FoVs) are concatenated into distinct slots. (b) shows a continuous TPR representation where FoVs are superimposed. (c) illustrates the limitations of the standard TPR compared to the proposed Soft TPR. The standard TPR only allows for a small, discrete set of valid representations, while the Soft TPR allows for a broader, continuous range.

This figure illustrates three different types of compositional representations: (a) shows a symbolic representation where factors of variation (FoVs) are concatenated into distinct slots; (b) shows a continuous TPR where FoVs are superimposed; (c) compares the discrete nature of TPRs with the continuous relaxation offered by Soft TPRs.
This figure illustrates the difference between symbolic and continuous compositional representations. (a) shows a symbolic representation where factors of variation (FoVs) are concatenated into distinct slots. (b) shows a continuous representation where FoVs are superimposed. (c) compares the TPR and Soft TPR, highlighting the discrete nature of TPR and the continuous relaxation in Soft TPR.
This figure compares three types of compositional visual representations: (a) shows the symbolic approach of disentanglement where each factor of variation (FoV) is allocated to a separate dimension. (b) illustrates the continuous TPR approach where FoVs are continuously superimposed. (c) highlights the key difference between TPR and Soft TPR; TPR has a strict algebraic structure that only allows a discrete set of points, unlike the relaxed Soft TPR that captures continuous regions in the representation space.

This figure illustrates the difference between symbolic and continuous compositional representations. (a) shows a symbolic representation where factors of variation are concatenated into discrete slots. (b) demonstrates a continuous representation where factors are superimposed as waves, forming a continuous blending. (c) compares the traditional TPR, limited to discrete points, with Soft TPR, which encompasses larger continuous regions. This highlights Soft TPR’s ability to better capture real-world data’s quasi-compositional nature and aligns better with continuous vector spaces of deep learning.

This figure illustrates three different ways of representing compositional structure. (a) shows the traditional disentangled representation as a concatenation of factors of variation (FoVs) in discrete slots. (b) shows a continuous representation where FoVs are superimposed to form a continuous representation. (c) compares the TPR (Tensor Product Representation) and Soft TPR, highlighting that TPRs form a limited discrete subset of points in a continuous vector space, while Soft TPRs occupy larger continuous areas, maintaining key TPR properties.

This figure illustrates three different ways to represent compositional structure. (a) shows a symbolic approach where factors of variation are concatenated into discrete slots. (b) shows a continuous approach (TPR) where factors are superimposed. (c) compares TPR and Soft TPR showing that Soft TPR allows a continuous relaxation of the rigid TPR specification.
This figure compares and contrasts three different types of compositional representations. (a) shows a symbolic representation where factors of variation (FoVs) are concatenated, similar to a string. (b) shows a continuous representation (Tensor Product Representation, TPR) where FoVs are superimposed as waves. (c) compares TPR and Soft TPR, highlighting the discrete and limited nature of TPR versus the continuous and expansive nature of Soft TPR.
This figure illustrates three different types of compositional representations: (a) symbolic compositional representations (disentangled representations), (b) continuous compositional representations (Tensor Product Representations), and (c) a comparison between TPR and Soft TPR. The symbolic representation uses discrete slots for each factor of variation (FoV), while the continuous representations combine FoVs continuously. Soft TPR extends TPR by relaxing the strict mathematical constraints of TPR, allowing for a broader representation of compositional structure.

This figure illustrates three different approaches to compositional representation. (a) shows the conventional disentanglement approach, where factors of variation (FoVs) are concatenated, resulting in a symbolic representation. (b) shows the TPR approach, which continuously superimposes FoVs for a continuous representation. (c) highlights the difference between TPR and Soft TPR, with the former being limited to a discrete set of points, while the latter occupies continuous regions in the representation space.
This figure illustrates the difference between symbolic and continuous compositional representations. (a) shows a symbolic representation where factors of variation are concatenated, like a string. (b) shows a continuous representation where FoVs are superimposed, like waves. (c) compares TPR and Soft TPR, highlighting Soft TPR’s relaxed constraint that allows for continuous representation learning.

This figure illustrates the difference between symbolic and continuous compositional representations. (a) shows a symbolic representation as a concatenation of distinct factors of variation (FoVs), while (b) depicts a continuous representation as a superposition of FoVs. (c) highlights the constraint of the traditional TPR, where only discrete points satisfy its specification, contrasted with the Soft TPR which allows for a continuous range of representations.

This figure illustrates the difference between symbolic and continuous compositional representations. Panel (a) shows a symbolic representation where factors of variation (FoVs) are concatenated, like a string. Panel (b) depicts a continuous representation where FoVs are superimposed, like waves. Panel (c) compares the Tensor Product Representation (TPR) and Soft TPR. TPR is highly constrained and only a small subset of points satisfy the TPR criteria, whereas Soft TPR is a continuous relaxation that encompasses a larger area.

This figure demonstrates the difference between symbolic and continuous compositional representations. (a) shows a symbolic representation as a concatenation of factors of variation (FoVs), while (b) shows a continuous representation as a superposition of FoVs. (c) highlights the limitations of the traditional TPR, which only allows a discrete subset of points in the representational space to qualify as TPRs, and how the proposed Soft TPR relaxes this constraint by capturing larger continuous regions.

This figure shows three different ways of representing compositional structure: (a) shows the symbolic, concatenative approach of disentanglement; (b) shows the continuous superposition of factors of variation (FoVs) as in Tensor Product Representation (TPR); (c) compares the discrete nature of TPR to the continuous relaxation of Soft TPR, highlighting the improved flexibility of Soft TPR.
This figure illustrates three different types of compositional representations: (a) symbolic compositional representation, (b) TPR, and (c) Soft TPR. The figure demonstrates that disentangled representations are symbolic in nature, as each factor of variation (FoV) occupies a discrete slot. In contrast, TPR and Soft TPR allow for a continuous representation of compositional structure. While TPRs are defined as points on a discrete manifold, Soft TPRs are continuous relaxations of TPRs, and are more easily learned by neural networks.

This figure illustrates the difference between symbolic and continuous compositional representations. (a) shows how disentangled representations are typically structured as concatenated factors of variation (FoVs). In contrast, (b) and (c) illustrate the Soft Tensor Product Representation (Soft TPR), a continuous approach that superimposes FoVs to create a holistic representation. (c) highlights that Soft TPR relaxes the strict constraints of the standard TPR, allowing representation learners greater flexibility.

This figure compares three different types of compositional representations. (a) shows a symbolic representation where factors of variation (FoVs) are concatenated. (b) shows a continuous representation using Tensor Product Representation (TPR) where FoVs are superimposed. (c) contrasts the discrete nature of TPR with the continuous relaxation offered by Soft TPR, highlighting Soft TPR’s ability to capture larger regions in the representational space.
This figure illustrates three different types of compositional representations. (a) shows a disentangled representation as a concatenation of factors of variation (FoVs), highlighting its symbolic and discrete nature. (b) introduces a continuous compositional representation (Soft TPR) where FoVs are blended together, emphasizing its continuous nature. (c) compares the TPR and Soft TPR, showing how Soft TPR relaxes the strict constraints of TPR to include more continuous regions of the representational space.
This figure illustrates three different ways of representing compositional structure: (a) shows a symbolic, discrete representation where each factor of variation (FoV) is allocated to a distinct slot. (b) shows a continuous representation where FoVs are superimposed. (c) compares TPR and Soft TPR. TPRs are highly constrained mathematically, resulting in only a small number of points in the representation space being valid. Soft TPRs relax this constraint, allowing a broader continuous region in the representation space to be valid.
This figure illustrates three different approaches for creating compositional representations. (a) shows a symbolic representation where each factor of variation (FoV) is allocated to a discrete slot. (b) shows a continuous representation where FoVs are superimposed. (c) compares the traditional Tensor Product Representation (TPR) which only allows for a discrete set of points in the representation space with the proposed Soft TPR, which allows for continuous regions.
This figure demonstrates three different ways of representing compositional structure. (a) shows the traditional disentangled representation, which is symbolic and discrete. (b) shows a continuous representation using Tensor Product Representation (TPR). (c) shows the proposed Soft TPR, a continuous relaxation of TPR that addresses some limitations of TPR by allowing for a wider range of continuous representational forms.

This figure illustrates the difference between symbolic and continuous compositional representations. (a) shows a symbolic representation as a concatenation of factors of variation (FoVs), which is a common approach in disentanglement. (b) shows a continuous representation using tensor product, where FoVs are superimposed. (c) compares TPR (discrete) and Soft TPR (continuous) in terms of the representational space, highlighting the relaxation in Soft TPR allowing for continuous representation of compositional structure.
This figure illustrates three different types of compositional representations: (a) shows a symbolic representation where factors of variation (FoVs) are concatenated, (b) shows a continuous representation where FoVs are superimposed, and (c) compares the discrete nature of traditional Tensor Product Representations (TPRs) to the continuous relaxation offered by Soft TPRs. The figure highlights the differences between symbolic and continuous approaches to compositional representation learning and the advantages of Soft TPRs in capturing continuous aspects of data.
This figure illustrates the difference between symbolic and continuous compositional representations. (a) shows a symbolic representation where factors of variation (FoVs) are concatenated into discrete slots. (b) shows a continuous representation (TPR) where FoVs are superimposed. (c) compares TPR and Soft TPR, highlighting that Soft TPR relaxes the strict requirements of TPR, allowing for larger continuous regions in the representational space.
This figure illustrates the difference between symbolic and continuous compositional representations. (a) shows a symbolic representation where factors of variation (FoVs) are concatenated, like a string. (b) shows a continuous representation where FoVs are superimposed, like waves. (c) compares TPR and Soft TPR. TPRs are limited to a discrete subset of points, while Soft TPRs occupy continuous regions. Soft TPRs offer enhanced flexibility while maintaining key TPR properties.
This figure illustrates the difference between symbolic and continuous compositional representations. (a) shows a symbolic representation where factors of variation (FoVs) are concatenated like a string. (b) shows a continuous representation (TPR) where FoVs are superimposed like waves. (c) compares TPR and Soft TPR, highlighting that Soft TPR relaxes the strict constraints of TPR while preserving its key properties.
This figure illustrates the difference between symbolic and continuous compositional representations. (a) shows a symbolic representation as a concatenation of tokens, (b) shows a continuous representation as a superposition of waves, and (c) compares the discrete TPR representation with the more relaxed Soft TPR representation.

This figure illustrates the difference between symbolic and continuous compositional representations. Panel (a) shows a symbolic representation where factors of variation (FoVs) are concatenated into distinct slots. Panel (b) shows a continuous representation (Tensor Product Representation or TPR) where FoVs are superimposed. Panel (c) highlights the limitations of TPRs, showing that only a discrete set of points in the representation space are valid TPRs. The proposed Soft TPR relaxes this constraint, allowing for a broader continuous set of valid representations.
This figure illustrates three different types of compositional representations. (a) shows a symbolic representation, where each factor of variation (FoV) is allocated to a discrete slot. (b) shows a continuous representation, where FoVs are continuously superimposed. (c) compares the traditional Tensor Product Representation (TPR) with the proposed Soft TPR, highlighting that Soft TPR relaxes the strict algebraic constraints of TPR, allowing for a more flexible and continuous representation of compositional structure.

This figure illustrates three different ways of representing compositional structure. (a) shows a symbolic representation, where factors of variation (FoVs) are concatenated, similar to a string. (b) demonstrates a continuous representation, where FoVs are superimposed as waves, representing a continuous blending. (c) compares the discrete nature of standard Tensor Product Representations (TPRs) with the continuous relaxation offered by Soft TPRs.
This figure compares three types of compositional representations: (a) shows the symbolic, discrete representation used in disentanglement; (b) shows the continuous representation using TPR; and (c) shows the continuous relaxation of TPR, Soft TPR, which is the main contribution of the paper. The figure highlights the differences in how the factors of variation are combined, showing the limitations of the discrete approach and the advantages of the continuous approaches, especially Soft TPR.
This figure illustrates three different types of compositional representations: (a) shows a symbolic representation where each factor of variation (FoV) is allocated to a discrete slot, (b) shows a continuous representation where FoVs are continuously blended together, and (c) compares the discrete TPR representation with the continuous Soft TPR representation. The symbolic representation is analogous to the way disentanglement models represent compositional structure, whereas Soft TPR aligns better with the continuous vector spaces used in deep learning.
This figure illustrates three different types of compositional representations. (a) shows a symbolic representation where factors of variation (FoVs) are concatenated. (b) shows a continuous representation where FoVs are superimposed using tensor product. (c) compares the discrete nature of standard TPR to the continuous relaxation offered by Soft TPR.
This figure illustrates three different ways of representing compositional structure. (a) shows a symbolic representation where factors of variation (FoVs) are concatenated into distinct slots. (b) shows a continuous representation (TPR) where FoVs are superimposed. (c) compares TPR and Soft TPR, highlighting that Soft TPR relaxes the strict constraints of TPR, allowing continuous representation of compositional structure within the continuous vector space of deep learning.
This figure illustrates three different types of compositional visual representations: (a) a symbolic representation using disentanglement, where each factor of variation (FoV) is assigned to a distinct slot; (b) a continuous representation using Tensor Product Representation (TPR), where FoVs are continuously blended; and (c) a continuous representation using Soft TPR, a relaxation of TPR that allows for more flexibility in the representational space. The figure highlights the key difference between symbolic and continuous compositional representations, emphasizing the benefits of Soft TPR in aligning with the continuity of deep learning vector spaces.

This figure illustrates three different approaches to compositional representations: (a) the symbolic, where factors of variation are concatenated into distinct slots, (b) the Tensor Product Representation (TPR), a continuous approach where factors are superimposed, and (c) the Soft TPR, a relaxation of TPR that allows for continuous representation and broader applicability.
This figure illustrates three different ways of representing compositional structure: (a) shows a symbolic approach where factors of variation (FoVs) are concatenated; (b) shows the continuous tensor product representation (TPR) where FoVs are superimposed; and (c) shows the Soft TPR, a relaxation of TPR that allows for continuous representations in larger regions of the representational space.
This figure compares different methods of representing compositional structures. (a) shows a symbolic representation where factors of variation are concatenated. (b) shows a continuous representation (TPR) where factors are superimposed. (c) compares TPR and Soft TPR, highlighting that Soft TPR relaxes the strict constraints of TPR allowing for a richer, more flexible continuous representation of compositional structure.

This figure illustrates the difference between symbolic and continuous representations of compositional structure. (a) shows a symbolic representation where factors of variation are concatenated into distinct slots. (b) shows a continuous representation where factors of variation are superimposed. (c) compares the TPR, which has a discrete set of valid representations, with the Soft TPR, which has a larger, continuous set of valid representations.
This figure illustrates three different ways of representing compositional structure. (a) shows the traditional disentangled representation as a concatenation of factors of variation (FoVs), similar to a string of symbols. (b) introduces the continuous TPR, where FoVs are continuously combined, akin to superposition of waves. (c) compares TPR and Soft TPR, highlighting the discrete nature of TPR points versus the continuous regions encompassed by Soft TPR, which allows for more flexible representation.

This figure illustrates the difference between symbolic and continuous compositional representations. Panel (a) shows a symbolic representation as a concatenation of factors of variation (FoVs), while panel (b) shows a continuous representation as a superposition of FoVs (waves). Panel (c) highlights that only a small subset of points satisfies the strict Tensor Product Representation (TPR) criteria, while Soft TPR relaxes these criteria, allowing for a larger continuous set of representations.

This figure illustrates three different types of compositional representations: (a) shows the traditional disentangled representation as a concatenation of factors of variation (FoVs), (b) shows the continuous tensor product representation (TPR) as a continuous superposition of FoVs, and (c) compares TPR and Soft TPR, highlighting that Soft TPR relaxes the strict algebraic constraints of TPR, allowing for a more flexible and continuous representation of compositional structure.
This figure shows three different ways to represent compositional structures: (a) shows a symbolic, discrete representation where factors of variation are allocated to distinct slots. (b) shows a continuous representation where factors are superimposed, analogous to waves. (c) compares traditional TPRs with Soft TPRs, highlighting that Soft TPRs relax the strict constraints of traditional TPRs, enabling continuous representation and more efficient learning.

This figure compares three different types of compositional representations: (a) symbolic compositional representations, where each factor of variation (FoV) is assigned to a discrete slot; (b) Tensor Product Representations (TPRs), where FoVs are continuously superimposed; and (c) Soft TPRs, which are a relaxed version of TPRs that allows for a continuous set of representations.
This figure compares three different types of compositional visual representations: (a) disentangled representation, (b) Tensor Product Representation (TPR), and (c) Soft TPR. The disentangled representation uses a concatenation of factors of variation, making it symbolic and discrete. TPR and Soft TPR, on the other hand, use a continuous superposition of factors of variation. However, TPR is constrained to a small subset of points in the vector space. Soft TPR relaxes this constraint to capture more continuous regions, making it better suited for continuous vector spaces of deep learning.
This figure compares three types of compositional representations: (a) a symbolic representation where factors of variation (FoVs) are concatenated into distinct slots, (b) a Tensor Product Representation (TPR) where FoVs are continuously superimposed, and (c) a Soft TPR, a continuous relaxation of TPR, allowing for a less restrictive and more flexible representation of compositional structure. The figure highlights the discrete nature of symbolic representations and the continuous, more flexible nature of the proposed Soft TPR in comparison to the original TPR.
This figure compares three different types of compositional representations: (a) shows a symbolic representation where factors of variation (FoVs) are concatenated into distinct slots. (b) shows a continuous representation (TPR) where FoVs are superimposed as waves. (c) compares TPR and Soft TPR, highlighting how Soft TPR relaxes the strict constraints of TPR while maintaining its core properties, leading to a more flexible and continuous representation of compositional structure.
This figure illustrates three different types of compositional representations: (a) a symbolic representation where factors of variation are concatenated, (b) a continuous tensor product representation (TPR) where factors are superimposed, and (c) a soft TPR, which is a relaxed version of TPR that allows for a more flexible, continuous representation.
This figure illustrates the difference between symbolic and continuous compositional representations, focusing on disentangled representations, Tensor Product Representations (TPR), and Soft TPR. Panel (a) shows disentangled representations as a concatenation of factors of variation (FoVs), highlighting the symbolic nature. Panel (b) depicts Soft TPR as a continuous superposition of FoVs. Panel (c) compares the discrete nature of TPRs with the continuous relaxation offered by Soft TPRs, showcasing the expanded space Soft TPR occupies within the representation space.
This figure illustrates three different types of compositional representations. (a) shows a symbolic representation where factors of variation (FoVs) are concatenated into distinct slots. (b) demonstrates a continuous representation (Tensor Product Representation or TPR) where FoVs are superimposed continuously. (c) compares TPR and Soft TPR, showing that TPRs only occupy a discrete subset of the representational space, while Soft TPRs occupy larger, continuous regions, making them easier to learn.

This figure illustrates three different ways to represent compositional structure. (a) shows a symbolic approach where factors of variation (FoVs) are concatenated into distinct slots. (b) shows a continuous approach where FoVs are superimposed. (c) compares the TPR and Soft TPR, highlighting that the Soft TPR allows for more flexible representations in continuous space.

This figure illustrates three different ways of representing compositional structure: (a) shows a symbolic, discrete representation where factors of variation are concatenated; (b) demonstrates a continuous representation using a tensor product, where factors are superimposed; and (c) compares the discrete TPR representation with a relaxed, continuous Soft TPR representation. The Soft TPR is shown to better leverage the continuity of vector spaces.

This figure illustrates the difference between symbolic and continuous representations of compositional structure. (a) shows a symbolic representation where factors of variation (FoVs) are concatenated into distinct slots. (b) shows a continuous representation using Tensor Product Representation (TPR) where FoVs are superimposed. (c) compares TPR and Soft TPR, highlighting Soft TPR’s relaxed constraint which allows for continuous regions in the representational space.

This figure illustrates the difference between symbolic and continuous compositional representations. (a) shows a symbolic representation where factors of variation (FoVs) are concatenated into distinct slots. (b) shows a continuous representation (TPR) where FoVs are superimposed. (c) compares TPR and Soft TPR, highlighting that Soft TPR relaxes the strict constraints of TPR, enabling the learning of a broader range of continuous representations.

This figure demonstrates three different types of compositional representations: (a) shows a disentangled representation as a concatenation of FoV tokens (colored blocks), (b) illustrates a continuous representation where FoVs are continuously superimposed to produce the overall representation, and (c) compares the TPR and Soft TPR representations, highlighting the difference in the number of points in the representational space that satisfy the TPR specifications.
This figure illustrates three different ways of representing compositional structure. (a) shows the traditional disentangled representation, where factors of variation are concatenated into a string-like structure. (b) shows the proposed Soft TPR, where factors of variation are continuously superimposed. (c) compares TPR and Soft TPR, showing that TPRs occupy a discrete subset of the representational space, while Soft TPRs occupy larger, continuous regions.

This figure illustrates the difference between symbolic and continuous compositional representations. (a) shows a symbolic representation where factors of variation (FoVs) are concatenated into distinct slots. (b) shows a continuous representation where FoVs are superimposed continuously. (c) compares the discrete nature of Tensor Product Representations (TPRs) with the continuous relaxation offered by Soft TPRs.
This figure illustrates three different ways of representing compositional structure. (a) shows a symbolic representation where factors of variation (FoVs) are concatenated like a string. (b) shows a continuous representation where FoVs are superimposed. (c) compares TPRs to Soft TPRs, showing how Soft TPRs relax the strict conditions of TPRs while preserving key properties.
This figure illustrates three different approaches to representing compositional structure in visual data. (a) shows the conventional disentangled representation, which is symbolic and discrete; each factor of variation (FoV) is assigned to a separate slot. In contrast, (b) presents the Tensor Product Representation (TPR), which is continuous; FoVs are superimposed to form a composite representation. (c) depicts a Soft TPR, which is a continuous relaxation of the TPR, combining the advantages of both approaches: it is continuous like TPR while maintaining the essential properties of TPRs. Soft TPRs overcome the limitations of the traditional TPR by allowing for more flexibility and expressiveness in the representational space.
This figure shows three different ways to represent compositional structure. (a) shows the symbolic, discrete representation of disentangled methods, which is a concatenation of factors of variation (FoVs). (b) shows the continuous representation using Tensor Product Representation (TPR). (c) compares the TPR and Soft TPR by illustrating the discrete space satisfied by TPR and the continuous space relaxed by Soft TPR.
This figure demonstrates three different ways to represent compositional structure. (a) shows a symbolic representation where each factor of variation (FoV) is assigned to a distinct slot, similar to string concatenation. (b) illustrates a continuous representation, where FoVs are continuously blended, akin to wave superposition. This is the core concept behind the TPR (Tensor Product Representation). Finally, (c) compares the traditional TPR with the proposed Soft TPR. The traditional TPR requires the representation to be on a discrete subset of points in the underlying space, while the Soft TPR relaxes this constraint, accommodating a wider range of continuous representations.

This figure demonstrates the difference between symbolic and continuous compositional representations. (a) shows a symbolic representation where features are concatenated into distinct slots. (b) illustrates a continuous representation where features are superimposed as waves, analogous to the Soft TPR. (c) compares the discrete nature of traditional TPRs to the continuous nature of the Soft TPRs, showing how Soft TPRs relax the strict requirements of traditional TPRs while preserving key properties.
More on tables
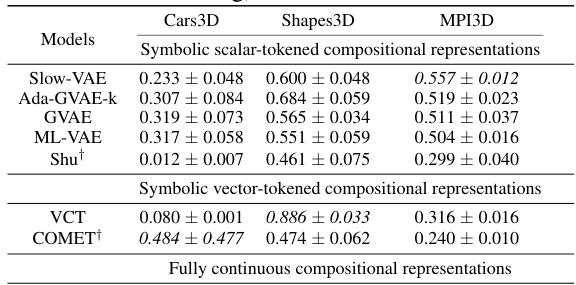
This table presents the FactorVAE and DCI disentanglement scores for different models on the Cars3D, Shapes3D, and MPI3D datasets. It compares the performance of various models, including those using symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representations. The results highlight the superior disentanglement performance achieved by the Soft TPR model proposed in the paper.
This table presents the FactorVAE and DCI disentanglement scores for different models on the Cars3D, Shapes3D, and MPI3D datasets. It compares the performance of various models, including symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representation models. The results show the Soft TPR model achieves state-of-the-art disentanglement across all three datasets.
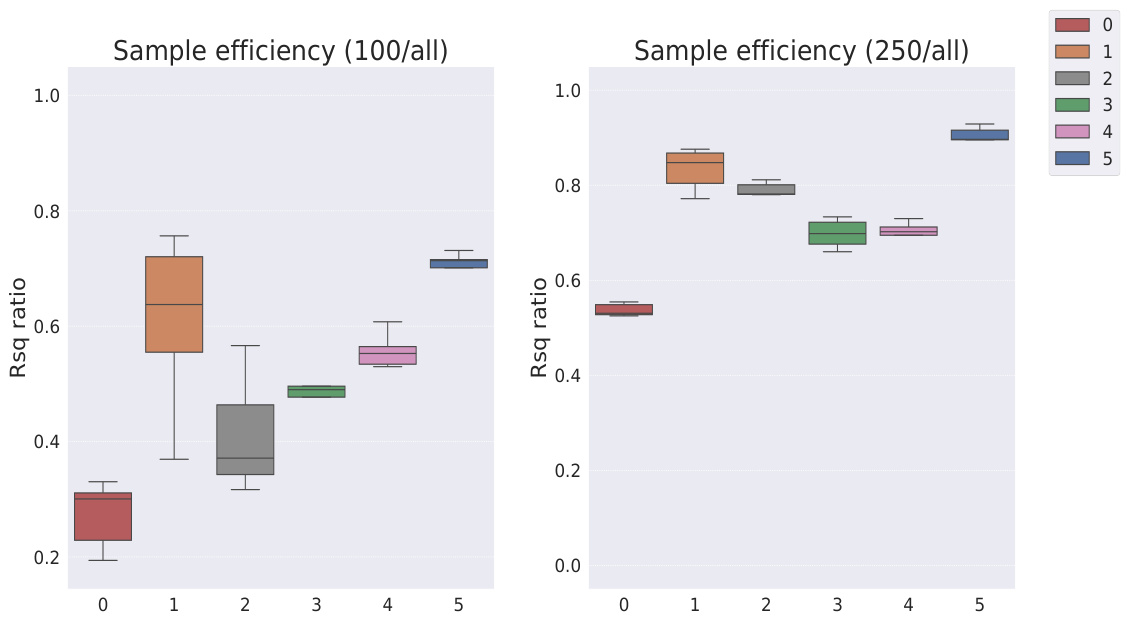
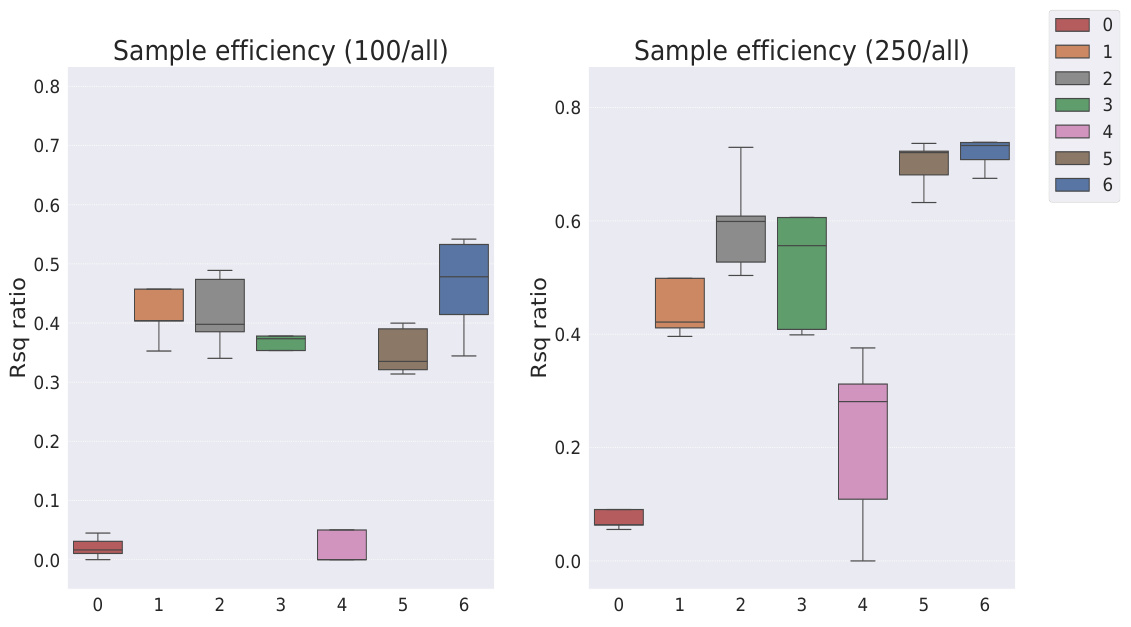
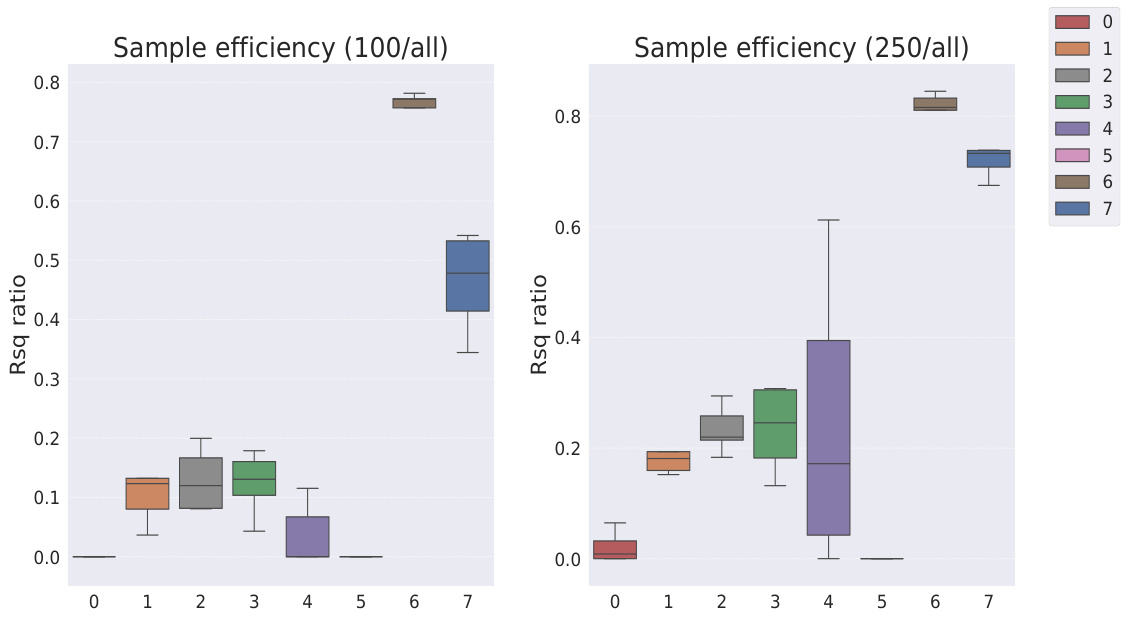
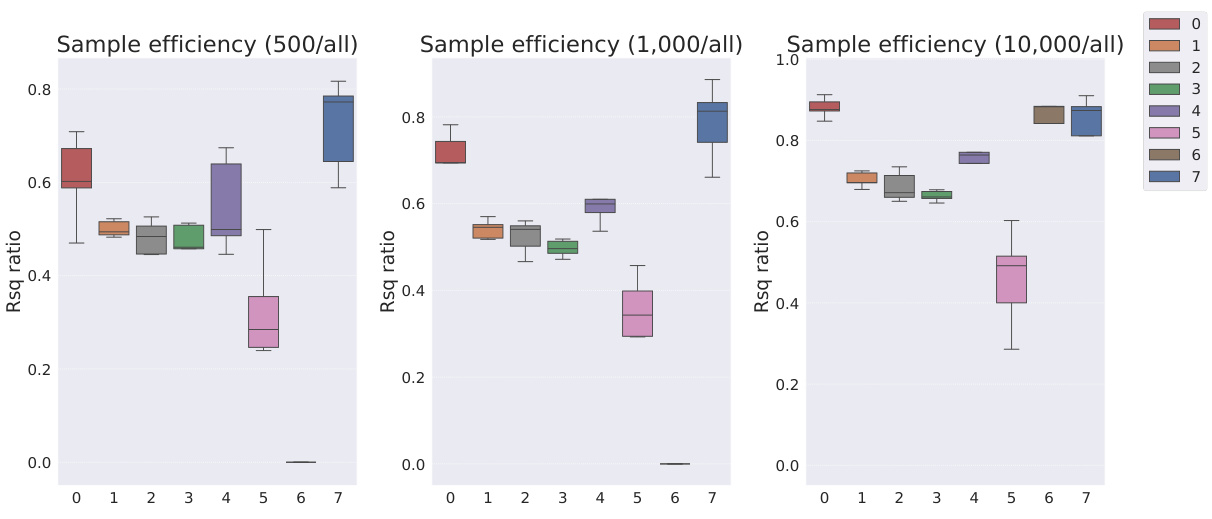
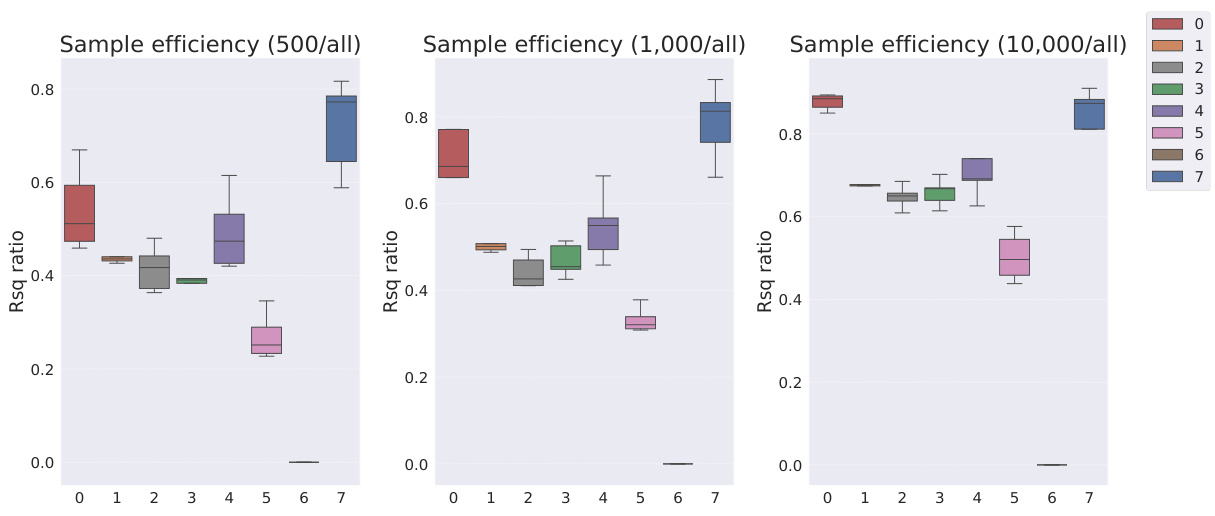
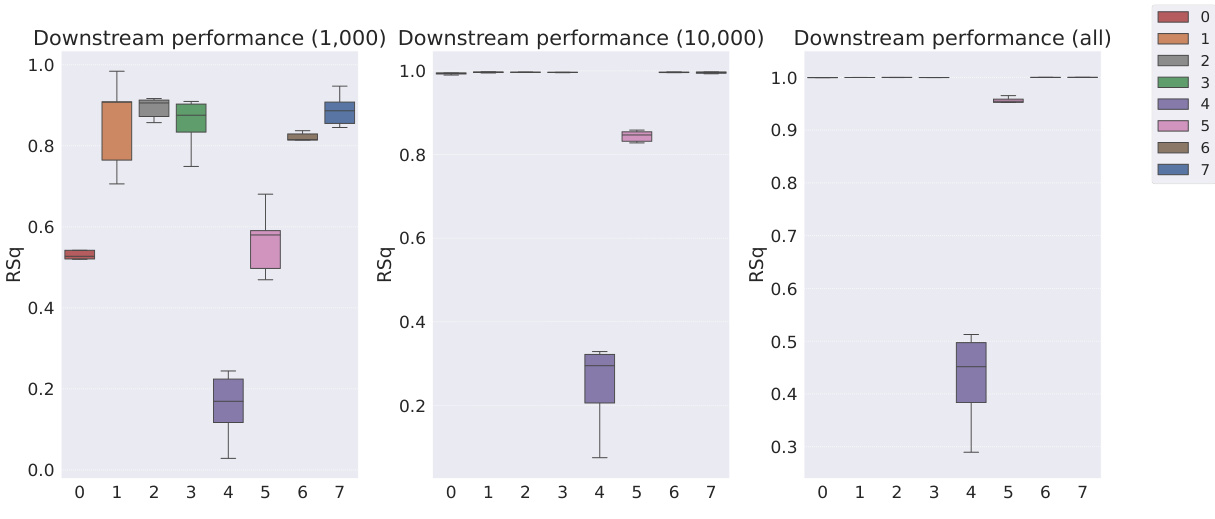
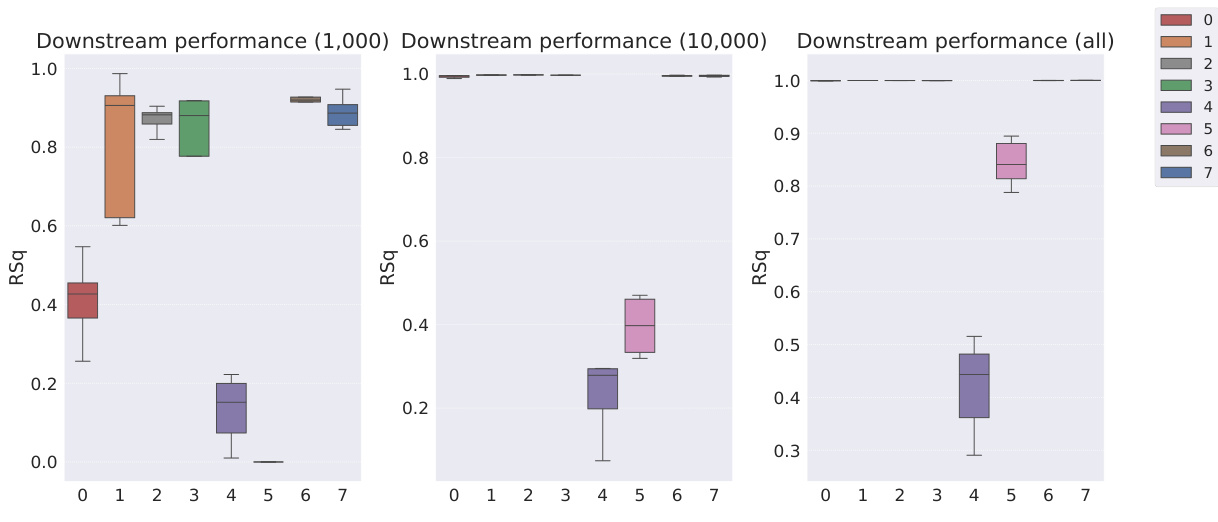
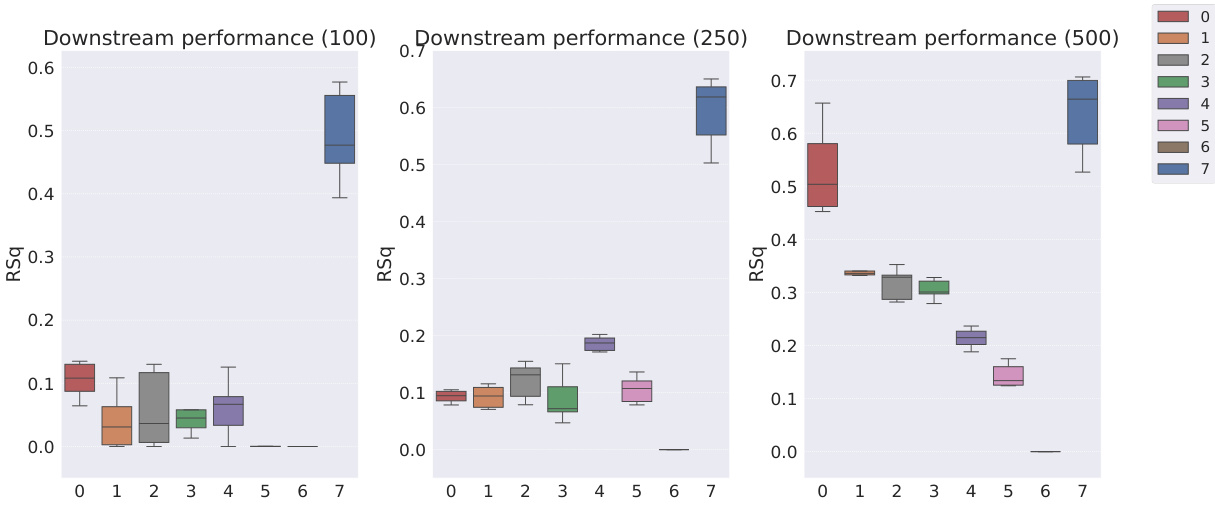
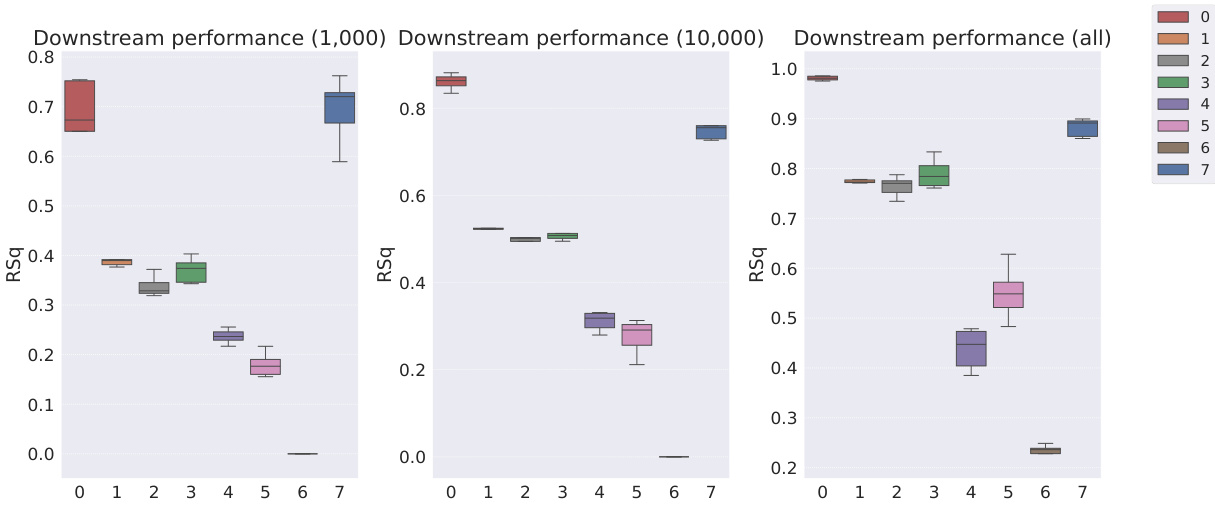
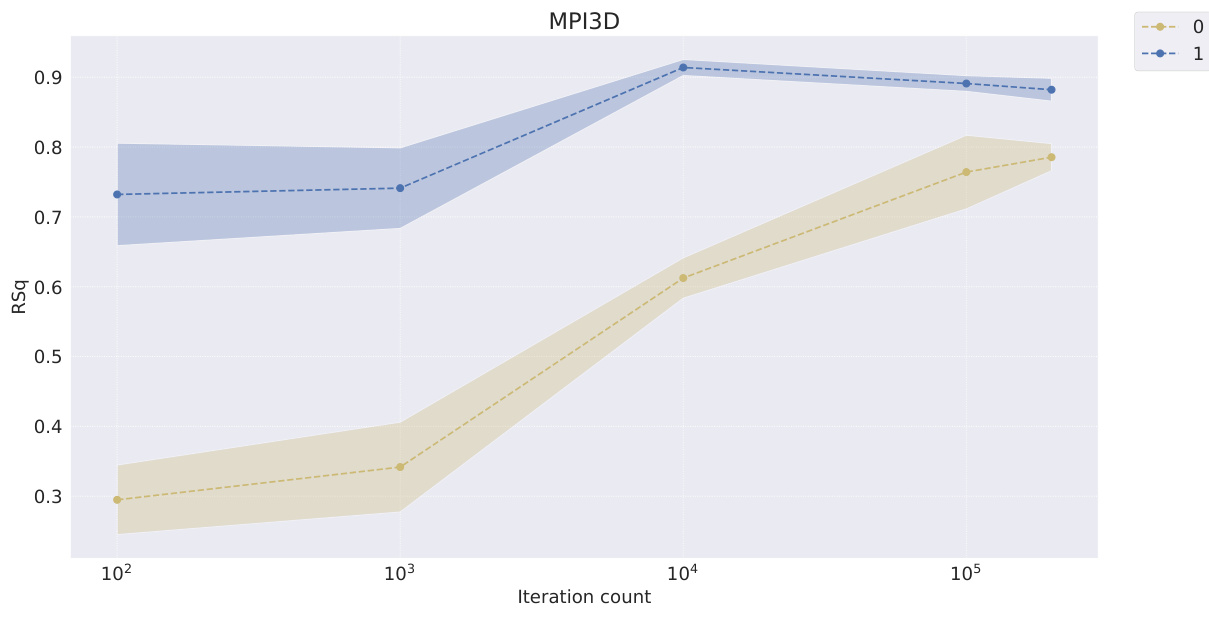
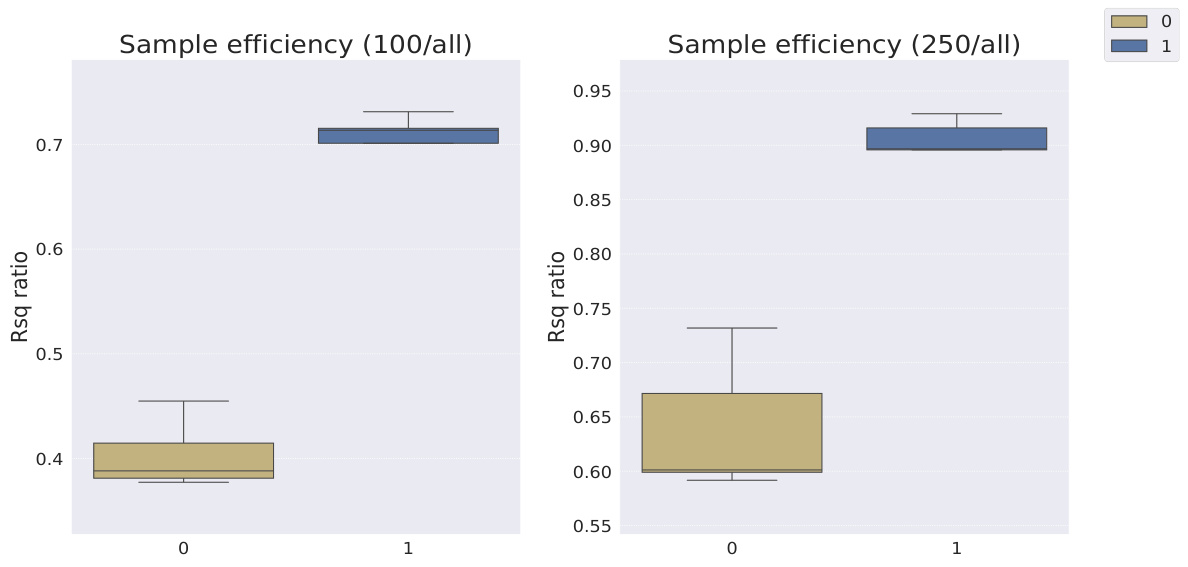
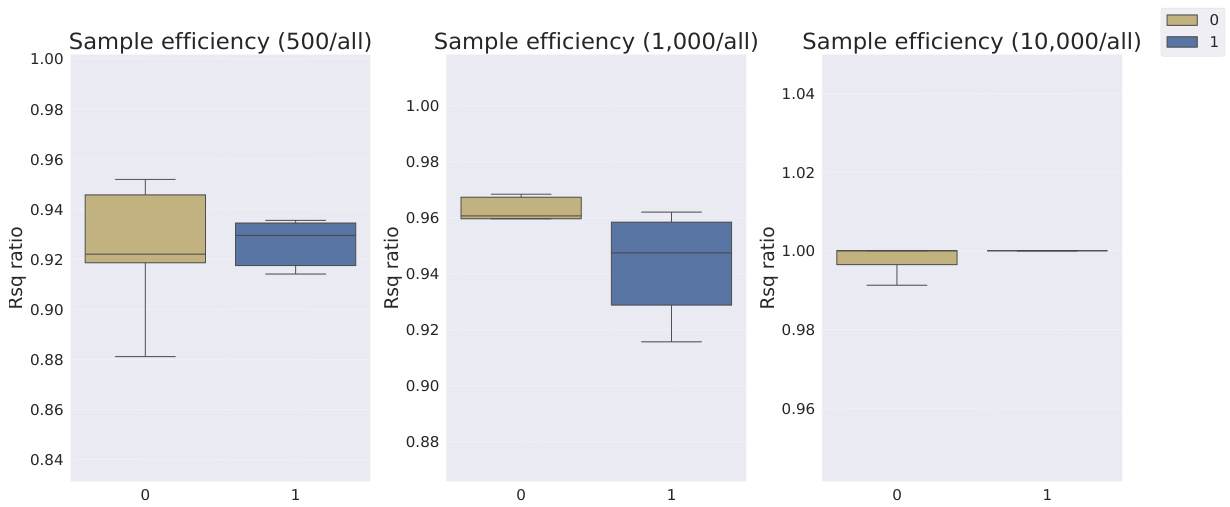
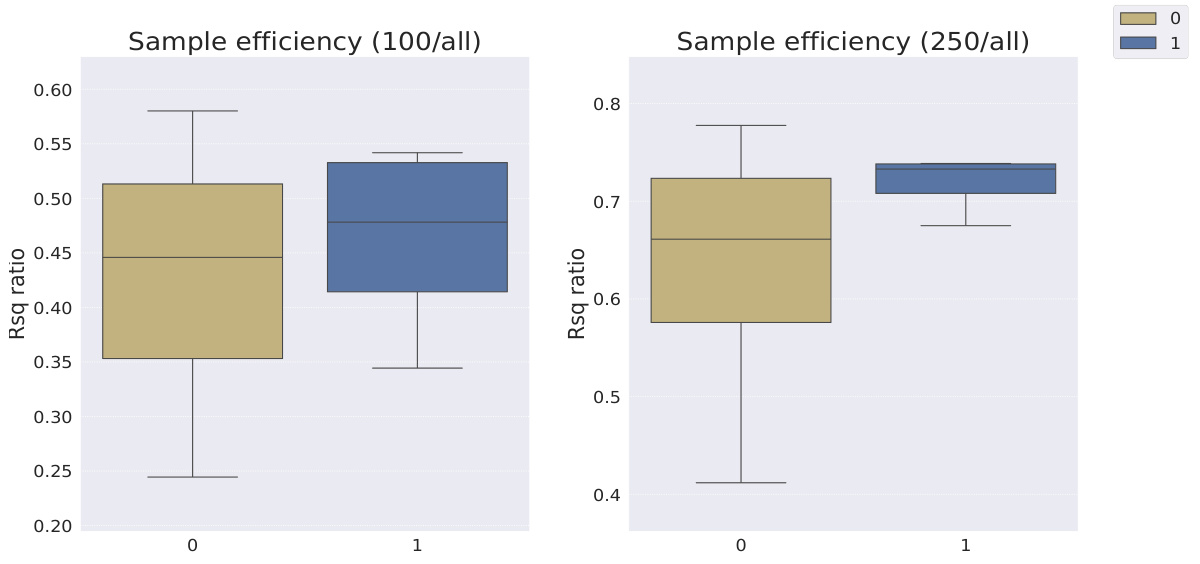
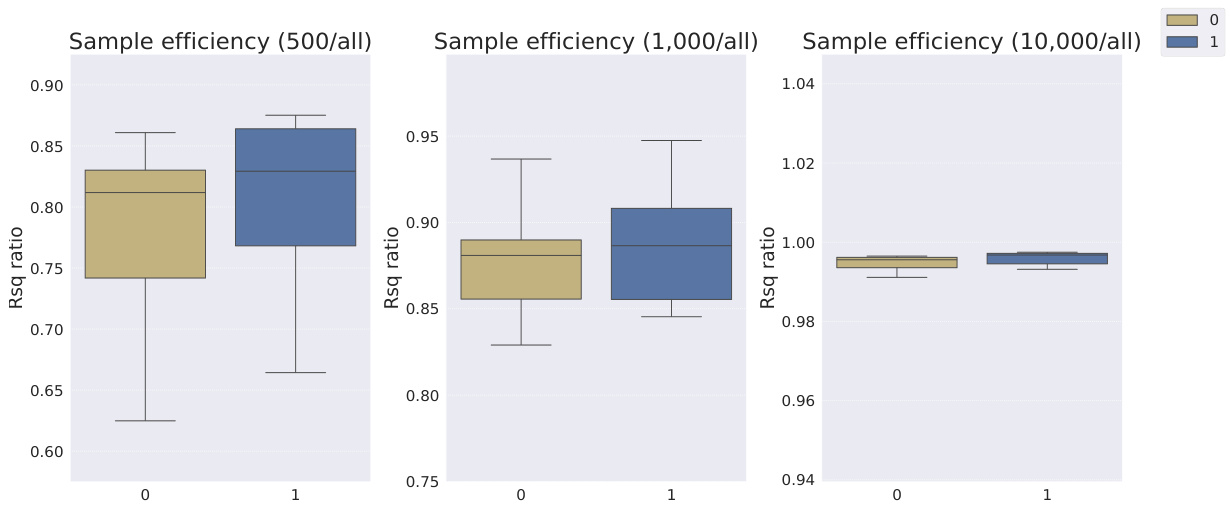
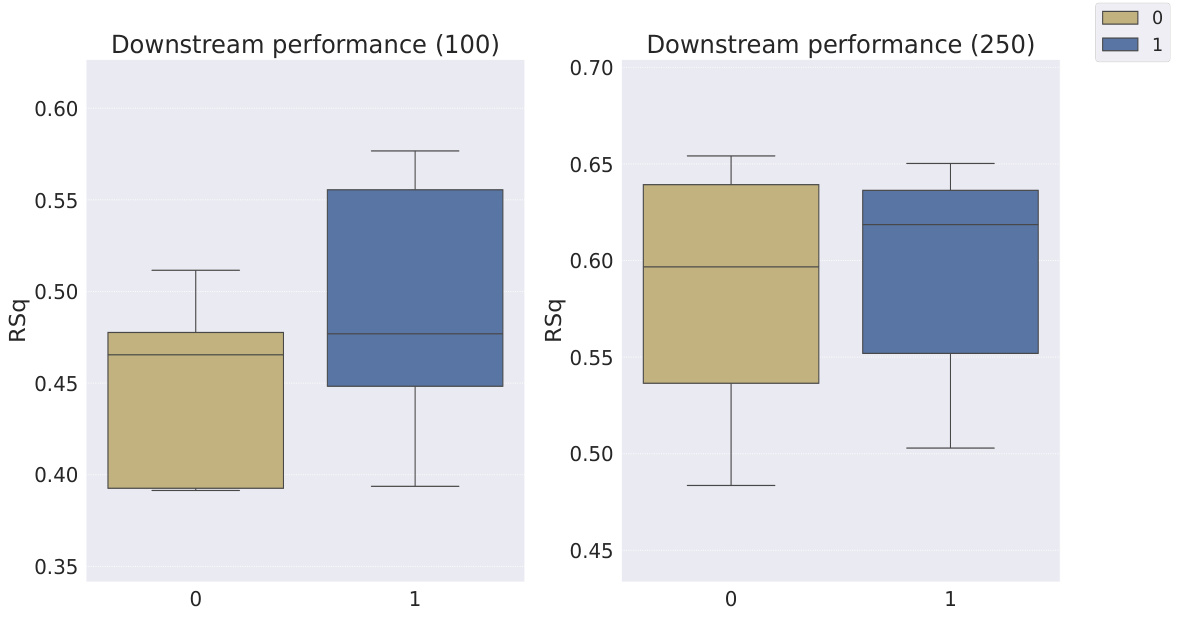
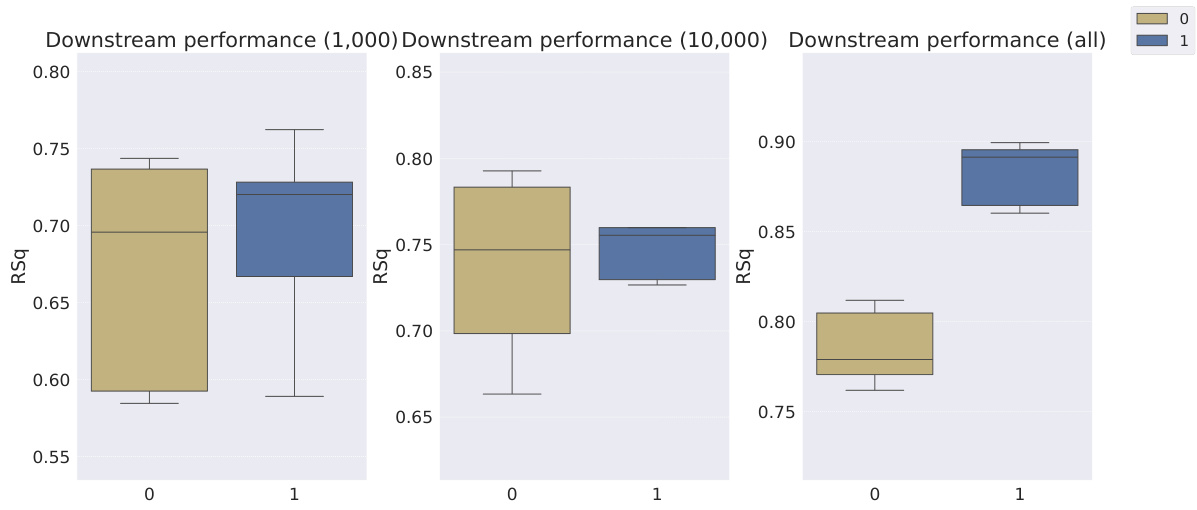
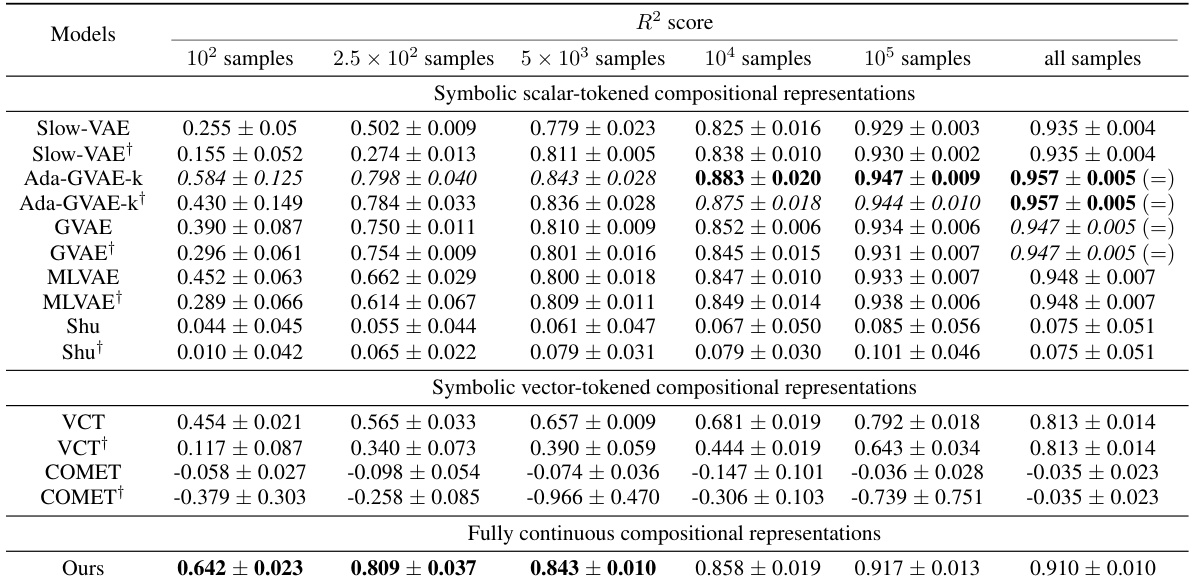
This table shows the R-squared scores and sample efficiencies of downstream regression models trained with different numbers of samples (100, 250, 500, 1000, 10000) from the MPI3D dataset. The odd columns represent the R-squared score, a measure of how well the model fits the data. The even columns show sample efficiency, which is the ratio of the model’s performance with a limited number of samples to its performance with all available samples. It compares different representation learning models, highlighting the sample efficiency of Soft TPR in the low sample regime.

This table presents the FactorVAE and DCI disentanglement scores for different models on the Cars3D, Shapes3D, and MPI3D datasets. It compares the performance of symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representation models. The scores provide a quantitative measure of how well each model disentangles the underlying factors of variation in the data. Higher scores indicate better disentanglement.

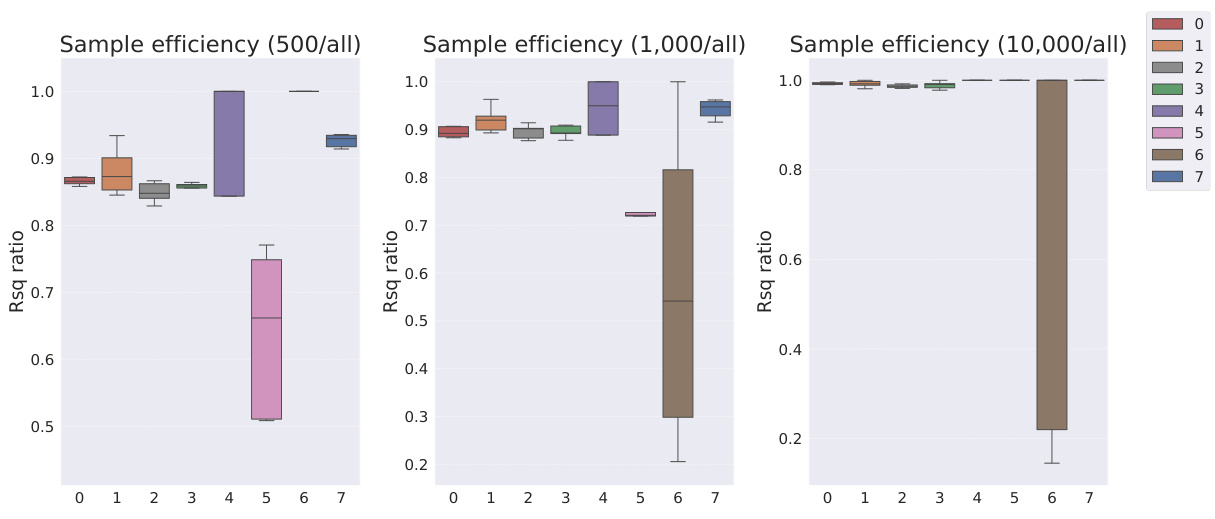
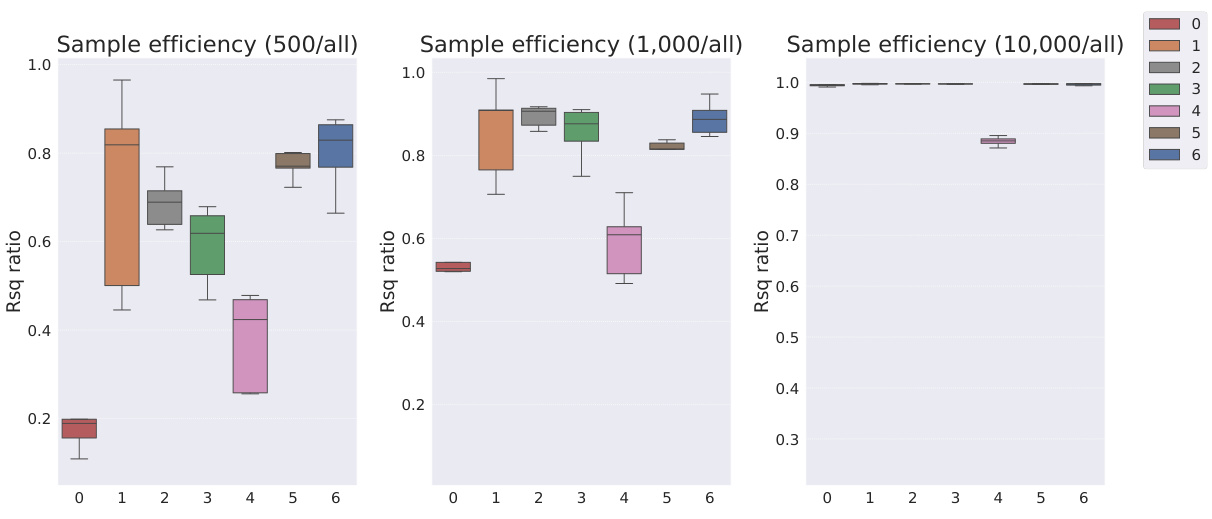
This table presents the sample efficiency results for the FoV regression task across three different datasets (Cars3D, Shapes3D, MPI3D). Sample efficiency is calculated as the ratio of the downstream model’s R-squared score when trained with a limited number of samples (100, 250, etc.) to its R-squared score when trained with all available samples. The table compares the sample efficiency of the Soft TPR model against the baseline models using the explicit TPR and the original variants of other baseline models. Higher values indicate better sample efficiency (i.e., the model performs well even with fewer samples).

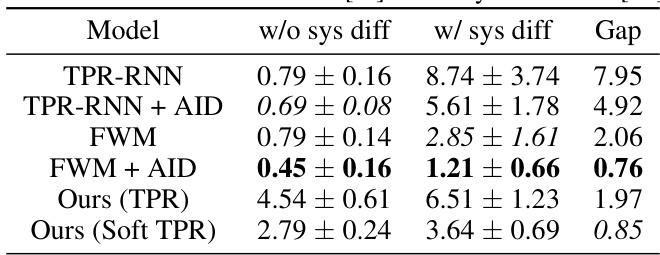
This table shows the results of an ablation study on the MPI3D dataset. The goal was to determine the contribution of different components of the Soft TPR Autoencoder model to disentanglement performance. The table compares DCI scores achieved under various conditions: with only weak supervision, with explicit filler dependency, with semi-orthogonality, and with all these properties included. The ‘Full’ row represents the complete model, demonstrating that all aspects contribute to superior disentanglement performance.

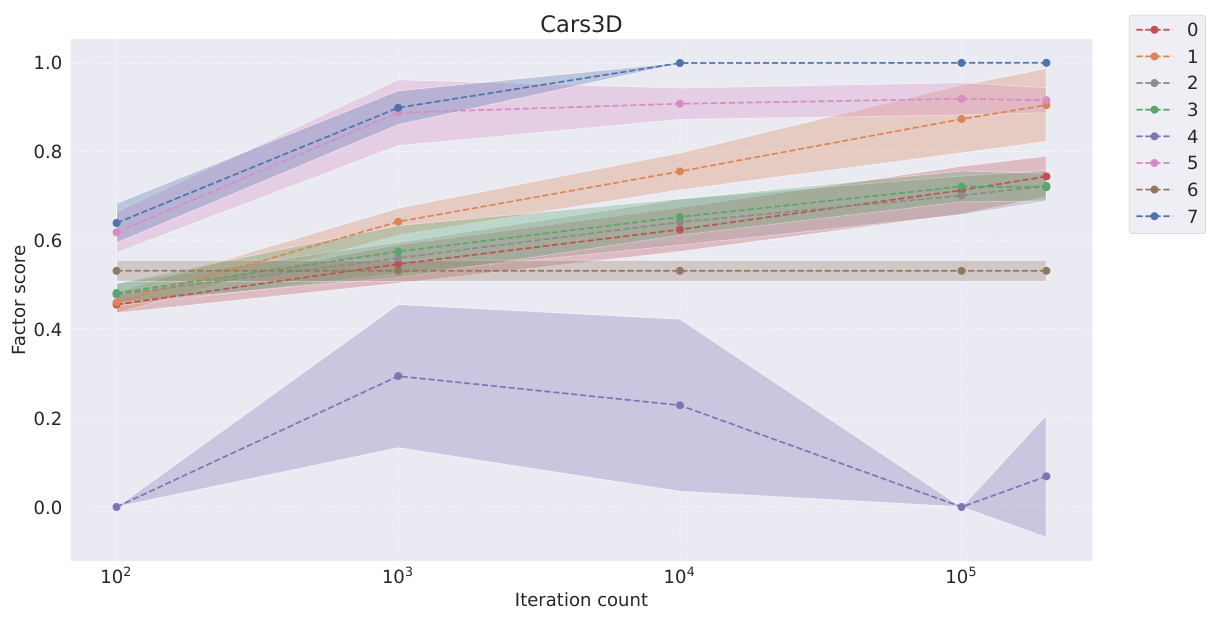
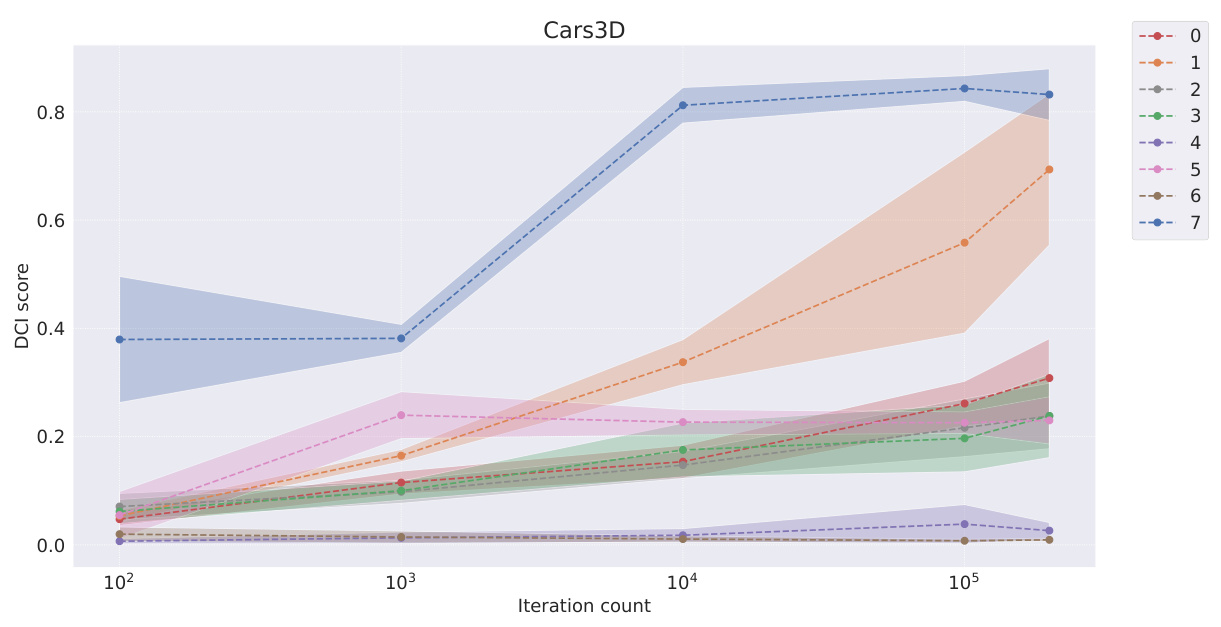
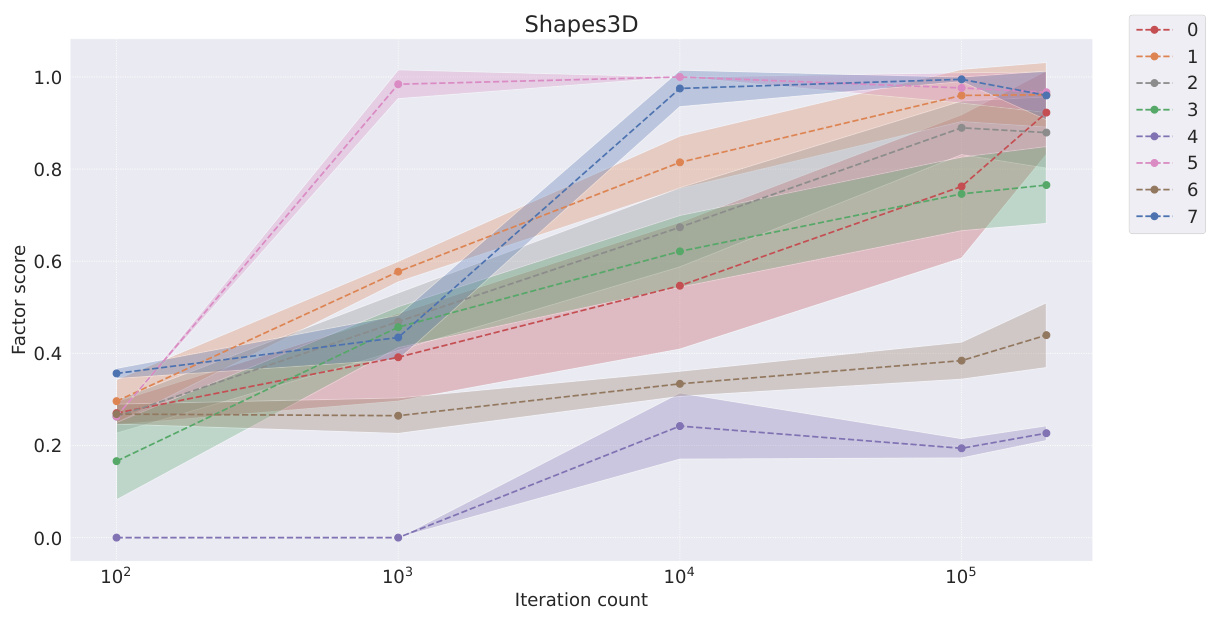
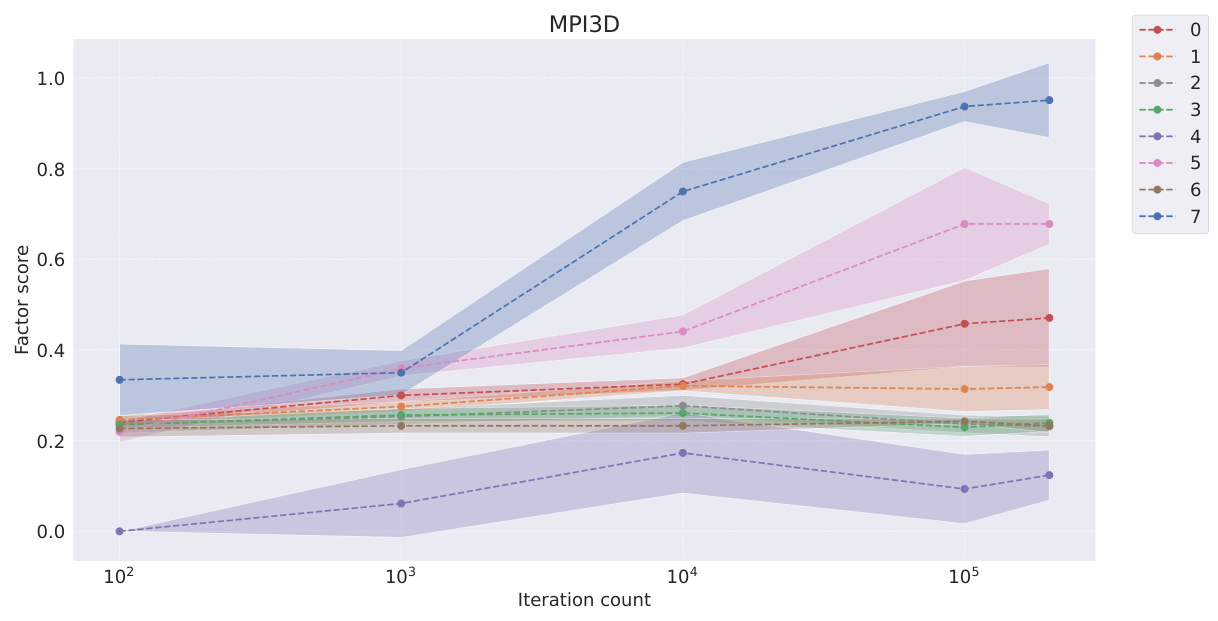
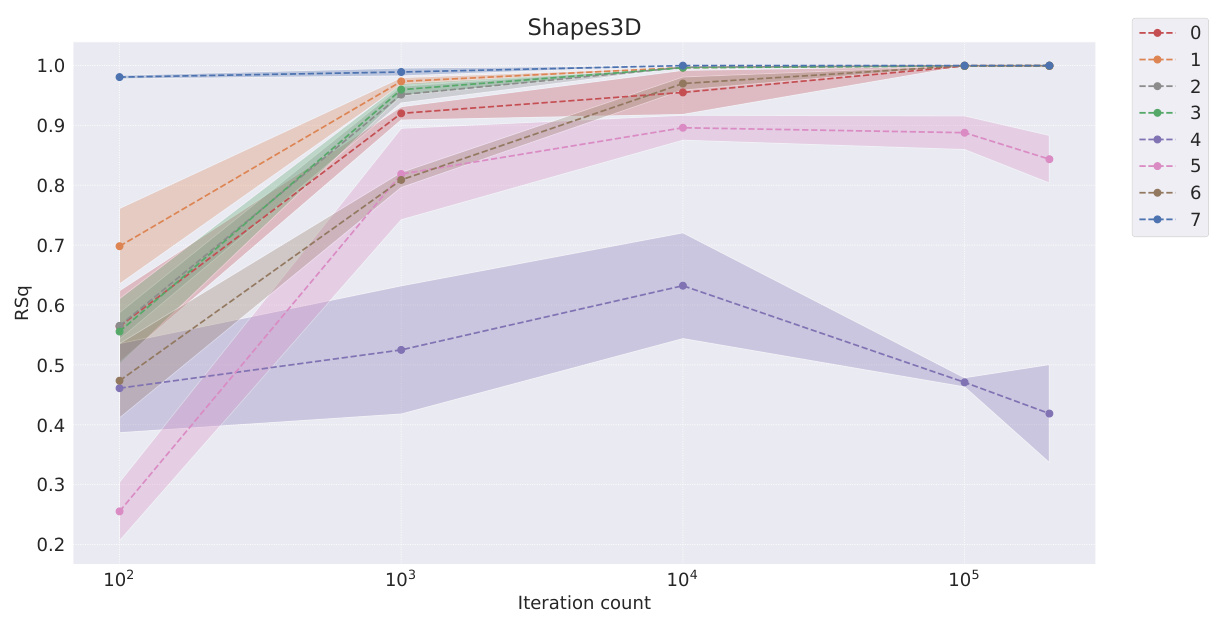
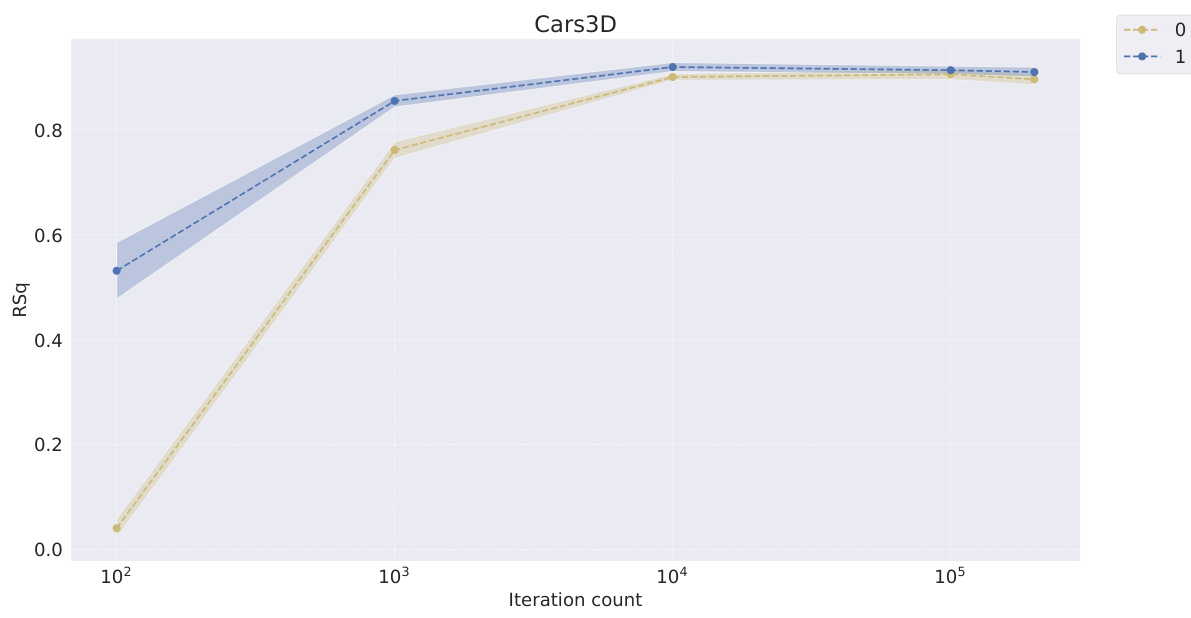
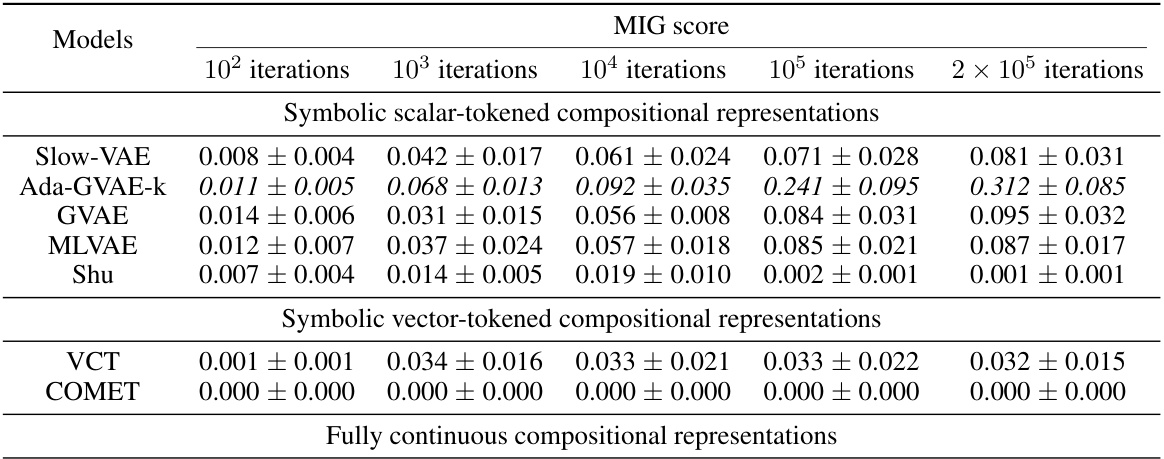
This table presents the FactorVAE scores achieved by different representation learning models at various stages of training (100, 1000, 10000, 100000, and 200000 iterations). It compares the performance of symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representation models. The table helps to evaluate how quickly different models learn the inherent compositional structure during the training process.

This table shows the FactorVAE scores achieved by different models at various training iterations (100, 1k, 10k, 100k, and 200k). The models are categorized into symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representations. It demonstrates the convergence rate of different representation learning approaches on the Cars3D dataset, specifically focusing on the FactorVAE score as a measure of disentanglement.

This table shows the FactorVAE scores achieved by different models at various training iterations (10^2, 10^3, 10^4, 10^5, and 2*10^5). The models are categorized into symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representation models. The table helps to compare the convergence speed and the final disentanglement level of different models. The ‘+’ symbol in the model names indicates a dimensionality-matched control group.

This table shows the hyperparameter values used for the Soft TPR Autoencoder model. It lists architectural hyperparameters (DR, NR, DF, NF) and loss function hyperparameters (λ1, λ2, β). The values are specified for three different datasets: Cars3D, Shapes3D, and MPI3D, indicating that the hyperparameters were tuned separately for each dataset. The ‘fixed’ notation for β indicates that this parameter was held constant across all datasets during the hyperparameter optimization process.

This table presents the FactorVAE and DCI disentanglement scores for different models on the Cars3D, Shapes3D, and MPI3D datasets. It compares the performance of symbolic scalar-tokened models (SlowVAE, Ada-GVAE-k, GVAE, ML-VAE, Shu), symbolic vector-tokened models (VCT, COMET), and the proposed fully continuous compositional representation (Ours). The results show that the Soft TPR significantly outperforms other methods in terms of disentanglement.

This table presents the FactorVAE and DCI disentanglement scores for different models on the Cars3D dataset. It compares the performance of various models, including symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representation models. The results are presented as means ± standard deviations, calculated over five random runs.
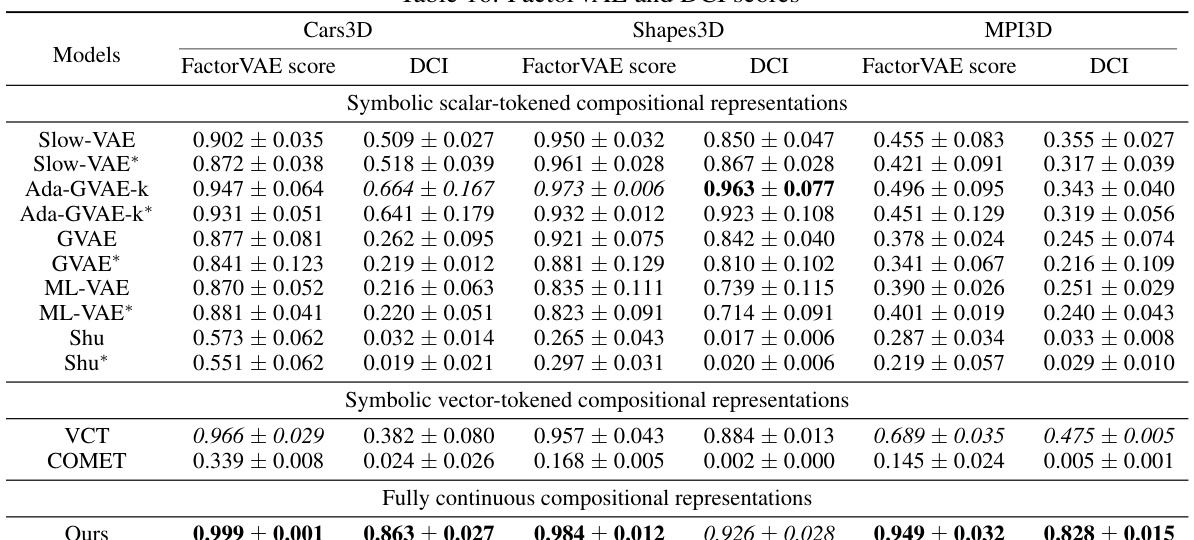
This table presents the FactorVAE and DCI disentanglement scores for different models on the Cars3D, Shapes3D, and MPI3D datasets. It compares the performance of various models, including symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representation models. The scores indicate the degree of disentanglement achieved by each model, with higher scores generally suggesting better disentanglement. The table also includes results for parameter-controlled models (denoted by *) which have an equivalent number of parameters to the Soft TPR model to ensure fair comparison. These models were created to rule out the impact of additional parameters on the disentanglement results.

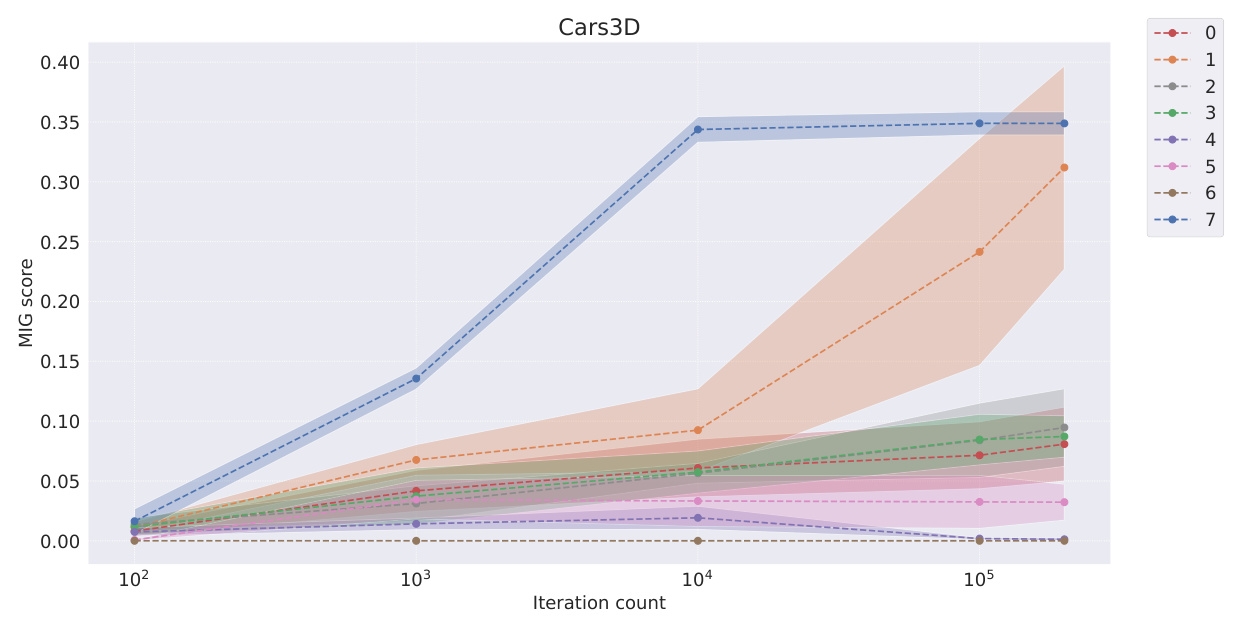
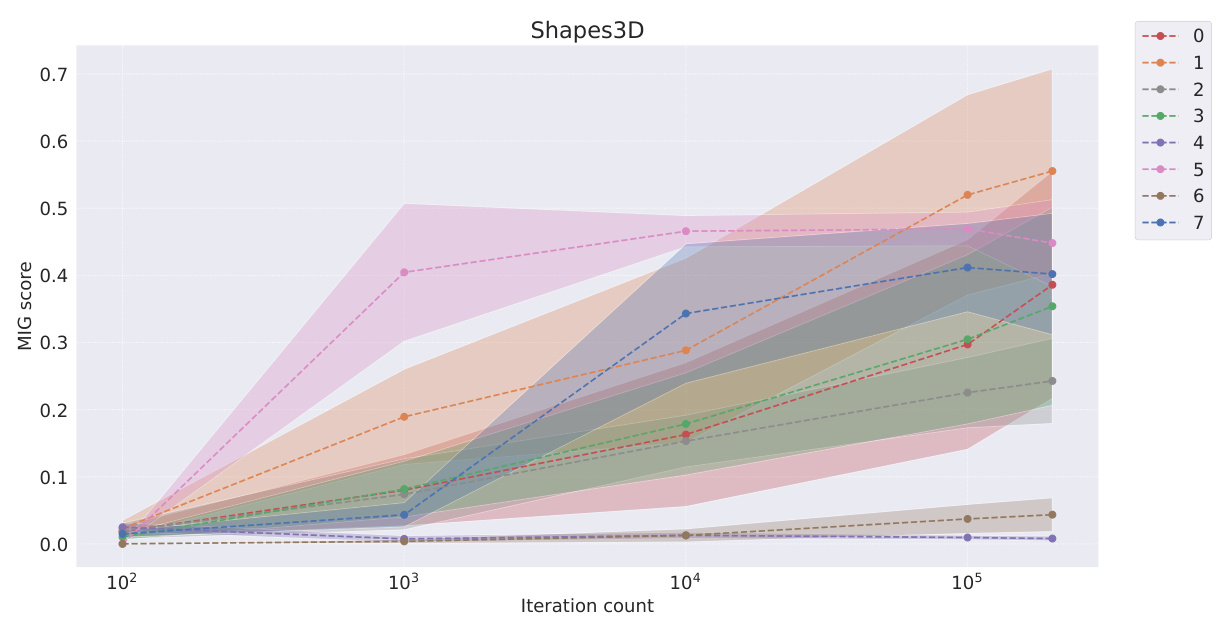
This table presents the BetaVAE and MIG scores for different models on three datasets (Cars3D, Shapes3D, MPI3D). The BetaVAE score and MIG score are two metrics used to evaluate the disentanglement of a representation learning model. Higher scores generally indicate better disentanglement. The models are categorized into symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representations. The table shows the performance of different models in achieving disentanglement. The ‘=’ symbol indicates that the score is 1.000, which is the maximum possible score for BetaVAE.

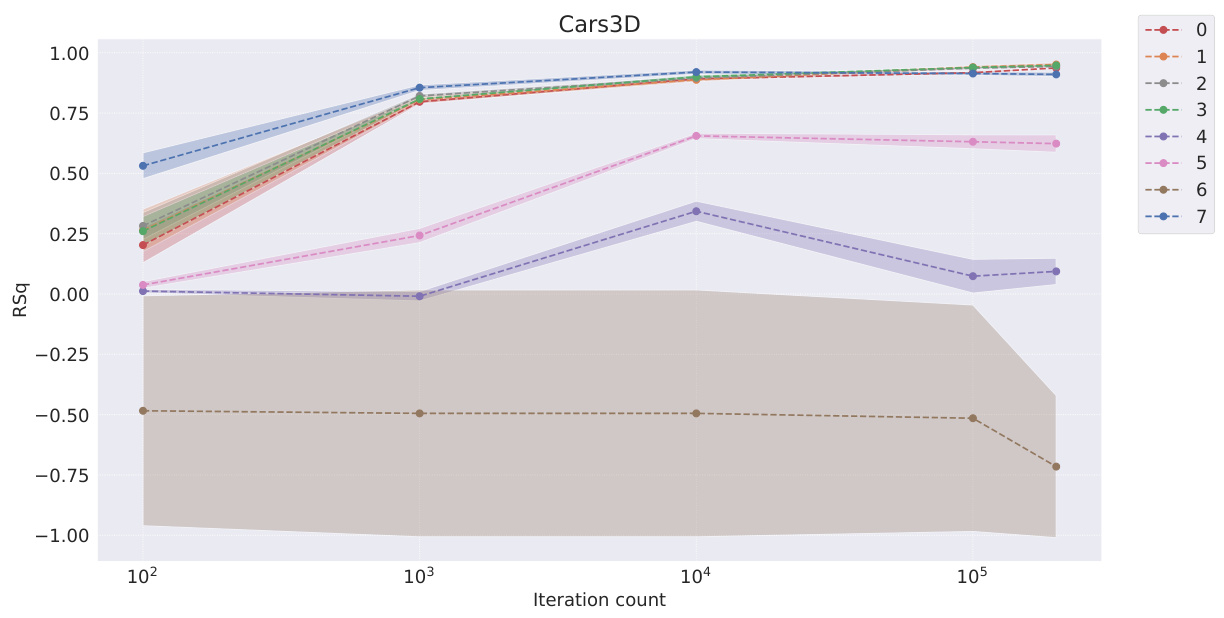
This table shows the FactorVAE scores achieved by different models at various training iterations on the Cars3D dataset. It compares the performance of symbolic scalar-tokened models (SlowVAE, Ada-GVAE-k, GVAE, MLVAE, Shu), symbolic vector-tokened models (VCT, COMET), and the proposed fully continuous compositional representation (Ours). The scores indicate the degree of disentanglement achieved by each model at different stages of training.

This table presents the FactorVAE and DCI disentanglement scores for different models on the Cars3D dataset. It compares the performance of various models, including symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representation models. The results show that the Soft TPR model achieves superior disentanglement compared to other models, particularly on the more challenging datasets.

This table presents the BetaVAE and MIG scores for different models across three datasets: Cars3D, Shapes3D, and MPI3D. The models are categorized into symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representations. Each model’s performance is evaluated at various stages of training, indicated by the number of iterations. The BetaVAE and MIG scores are metrics for evaluating the disentanglement of the learned representations.
This table presents the BetaVAE and MIG disentanglement scores for different models across three datasets (Cars3D, Shapes3D, MPI3D). The models are categorized into symbolic scalar-tokened compositional representations, symbolic vector-tokened compositional representations, and fully continuous compositional representations. The scores represent the average performance over five random runs, providing a measure of how well each model separates the factors of variation in the data.

This table presents the FactorVAE scores for different models at various iterations during training. It compares the performance of symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representation models. The results show how the FactorVAE score changes over time for each model, indicating the models’ convergence rate and the quality of the disentangled representations learned.
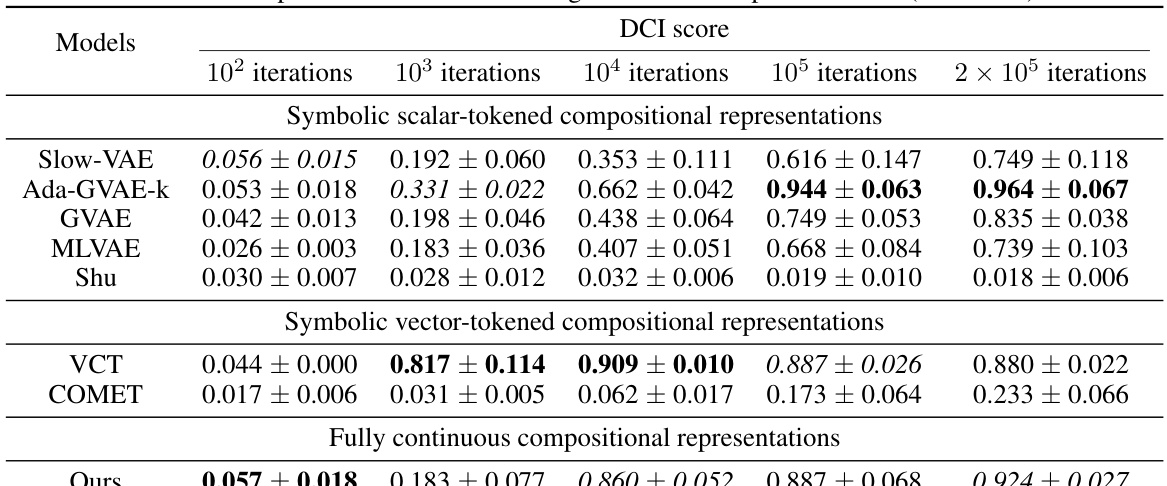
This table presents the FactorVAE and DCI disentanglement scores for different models on the Cars3D dataset. It compares the performance of various models, including those using symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representations. The table shows the scores obtained at different stages of training (100, 1000, 10000, 100000, and 200000 iterations). It highlights the superior disentanglement performance achieved by the Soft TPR model compared to traditional approaches.

This table presents the FactorVAE and DCI disentanglement scores for different models on the Cars3D, Shapes3D, and MPI3D datasets. The models are categorized into symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representations. The table allows for a comparison of the disentanglement performance of different representation learning approaches, highlighting the superior performance of the proposed Soft TPR model.
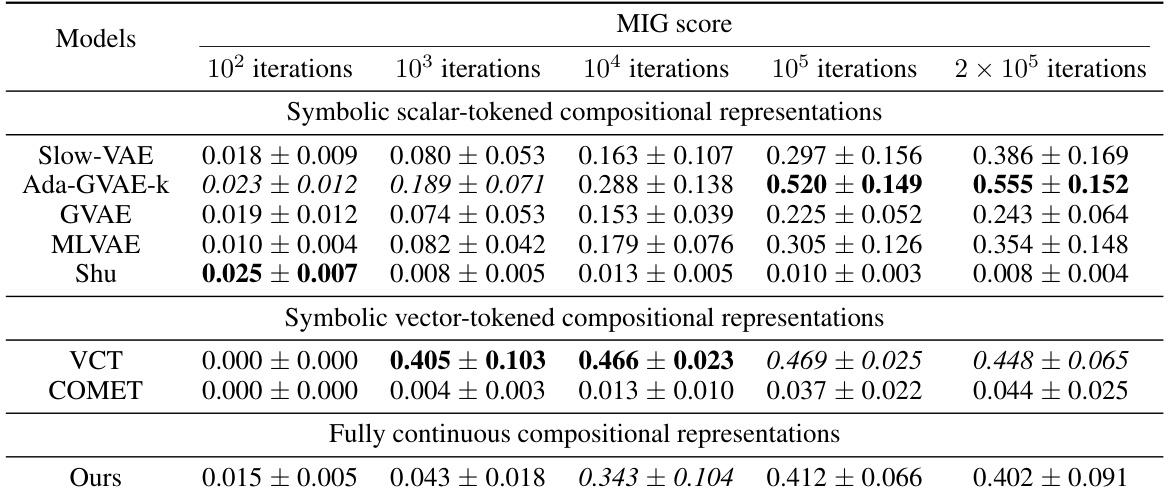
This table presents the BetaVAE and MIG disentanglement scores for different models on three datasets (Cars3D, Shapes3D, MPI3D). The models are categorized into symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representation models. The scores are presented for various stages of training (iterations 100, 1000, 10000, 100000, 200000), allowing for an analysis of convergence speed and the final disentanglement performance of each model.

This table presents the FactorVAE and DCI disentanglement scores for different models on the Cars3D dataset. It compares various models, including symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representation models. The scores indicate the level of disentanglement achieved by each model, where higher scores represent better disentanglement. The table highlights the superior performance of the proposed Soft TPR model compared to existing approaches.
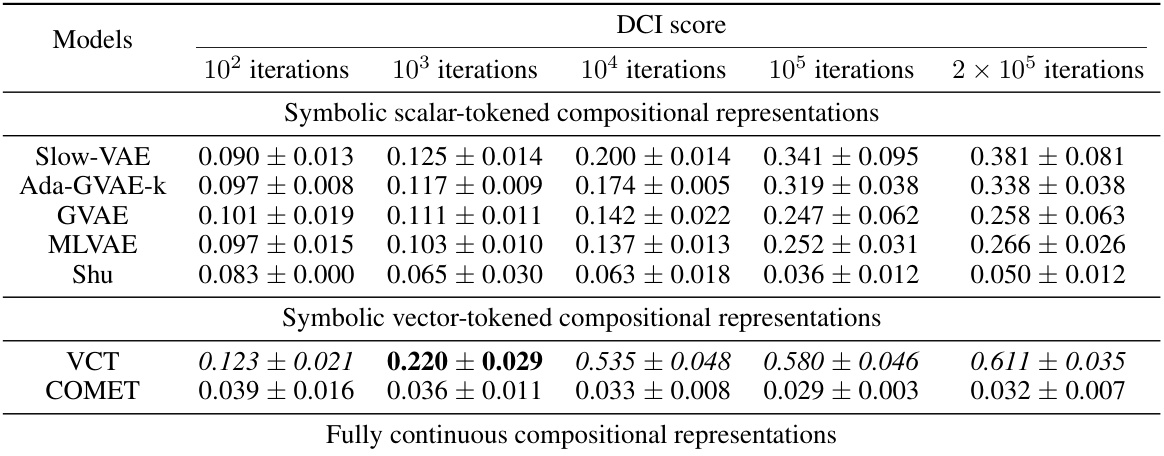
This table presents the FactorVAE and DCI disentanglement scores for different models on the Cars3D dataset. It compares the performance of various models, including symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representations. The scores indicate the degree of disentanglement achieved by each model, with higher scores representing better disentanglement.
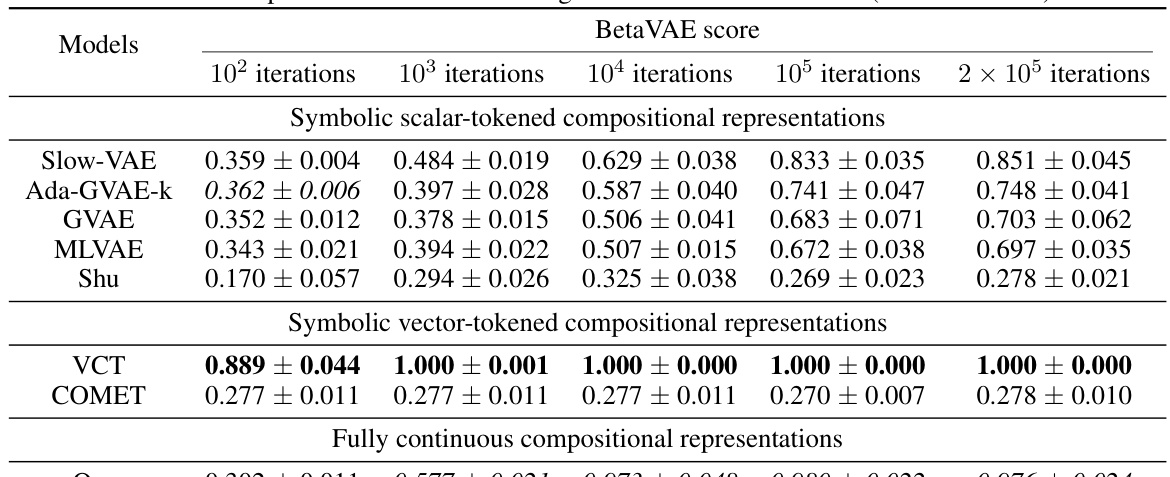
This table presents the BetaVAE and MIG disentanglement scores for different models across three datasets (Cars3D, Shapes3D, MPI3D). It shows the scores at various stages of training (iterations). The models are categorized into symbolic scalar-tokened compositional representations, symbolic vector-tokened compositional representations, and fully continuous compositional representations. The table allows for comparison of disentanglement performance between different model types and the impact of training duration on disentanglement.
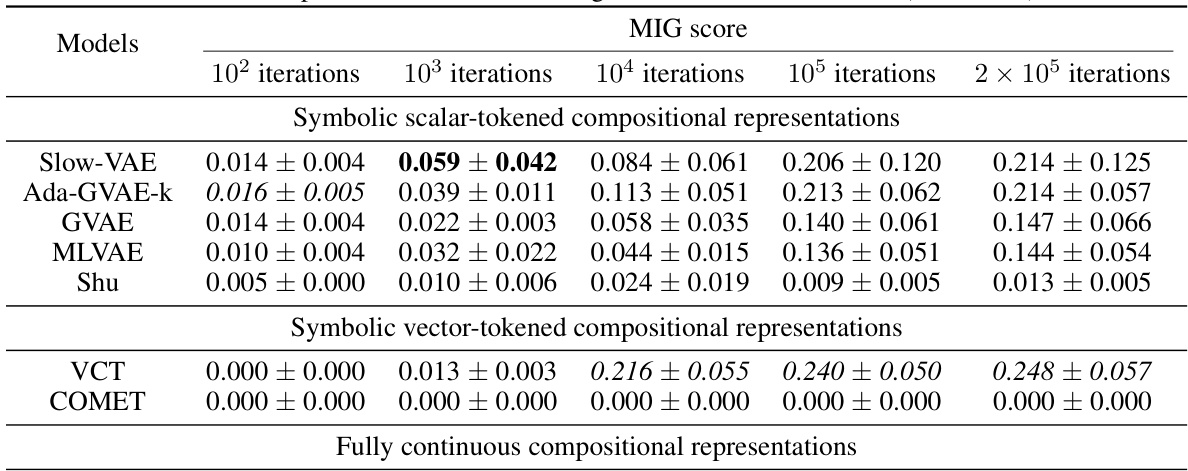
This table presents the BetaVAE and MIG disentanglement scores for different models, categorized by their representational type (symbolic scalar-tokened, symbolic vector-tokened, and fully continuous). The scores are shown for different stages of training (100, 1,000, 10,000, 100,000, and 200,000 iterations) across three datasets (Cars3D, Shapes3D, MPI3D). The table allows for the comparison of disentanglement levels achieved by different models and across different training stages, highlighting the performance of the Soft TPR Autoencoder.
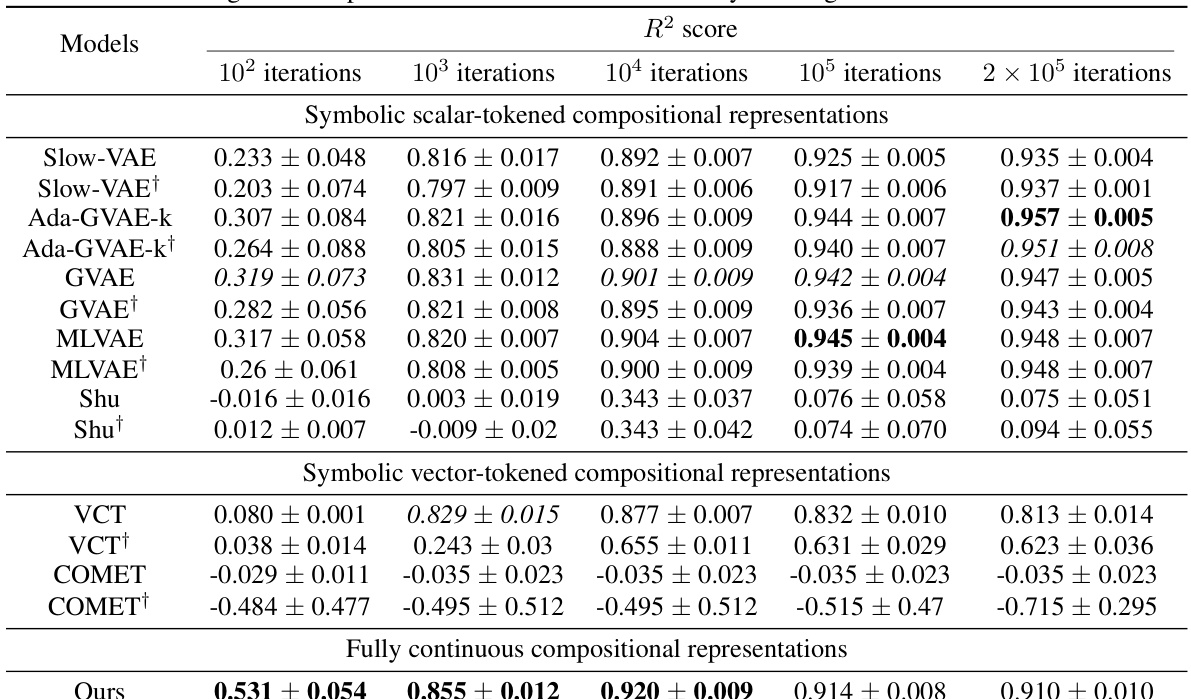
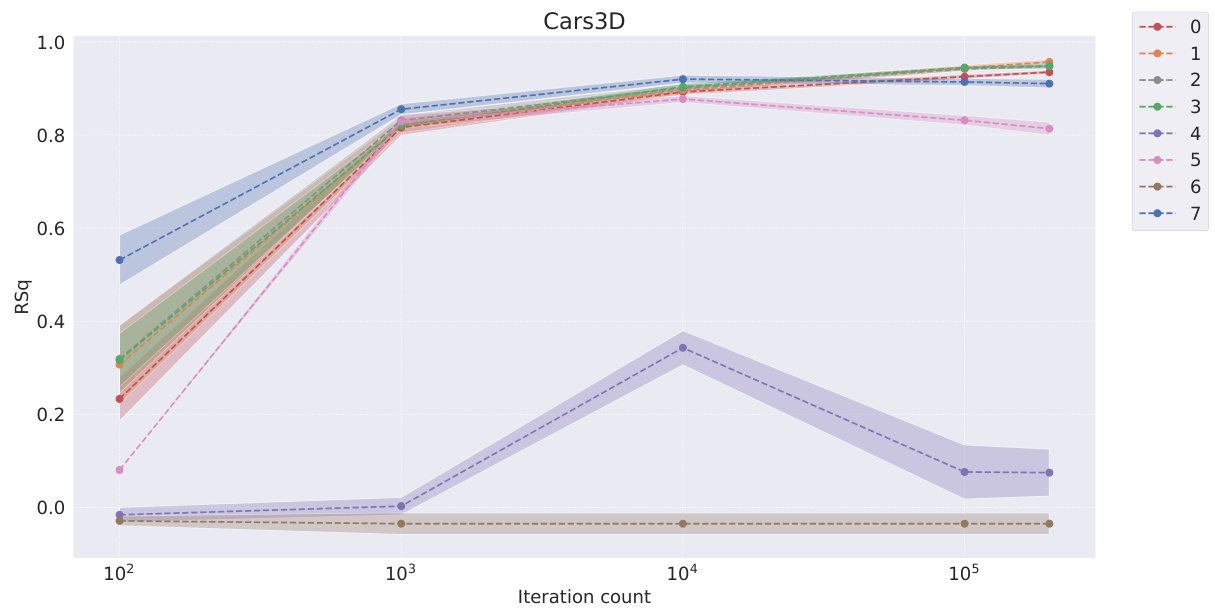
This table presents the FactorVAE scores achieved by different representation learning models at various training iterations (100, 1k, 10k, 100k, and 200k iterations). It compares the performance of models employing symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representations, highlighting the convergence speed and the final performance of each approach on the Cars3D dataset for disentanglement.

This table presents the FactorVAE scores achieved by different representation learning models at various stages of training (10 2, 10 3, 10 4, 10 5, and 2 × 10 5 iterations). The models are categorized into symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representation models. The table showcases how the FactorVAE score, a metric for measuring disentanglement, changes over time for each model, offering insights into their convergence rates. The results show the performance of each model on the Cars3D dataset in terms of achieving disentangled representations.
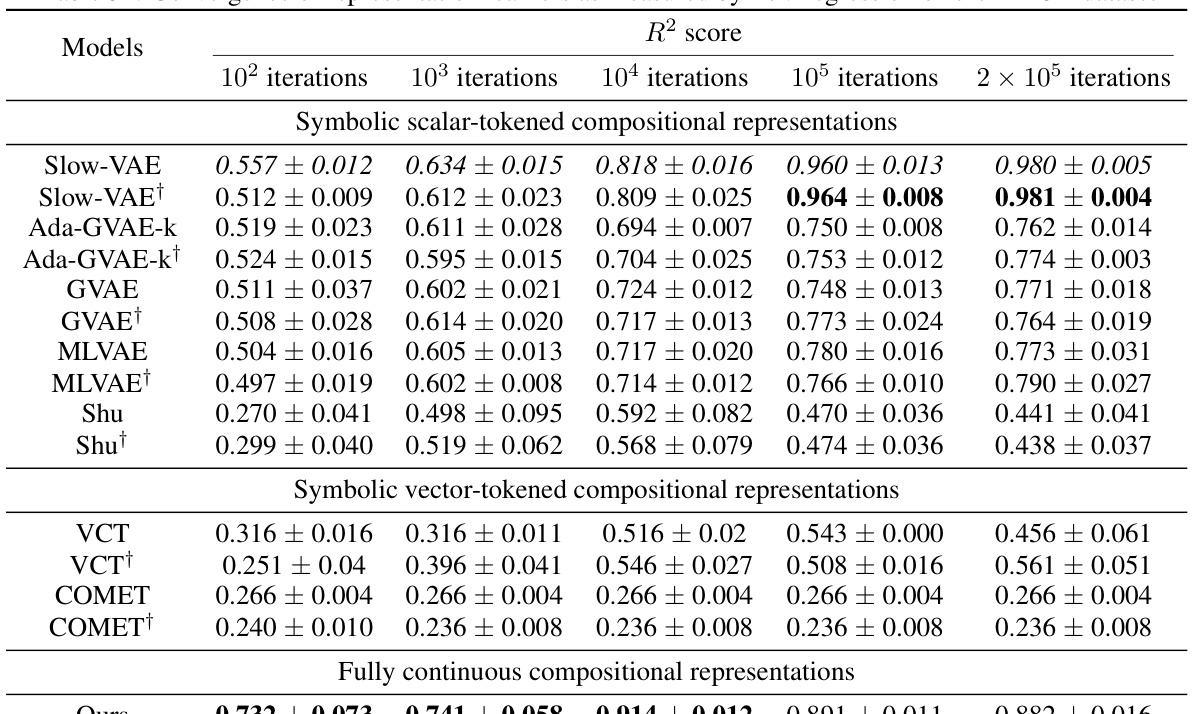
This table presents the FactorVAE scores achieved by different representation learning models at various stages of training (10 2, 103, 104, 105, and 2 × 105 iterations). The models are categorized into symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representations. The table shows how the FactorVAE score, a metric for evaluating the degree of disentanglement, changes as the models train. This allows for a comparison of how quickly different representation learning methods converge toward a disentangled representation.

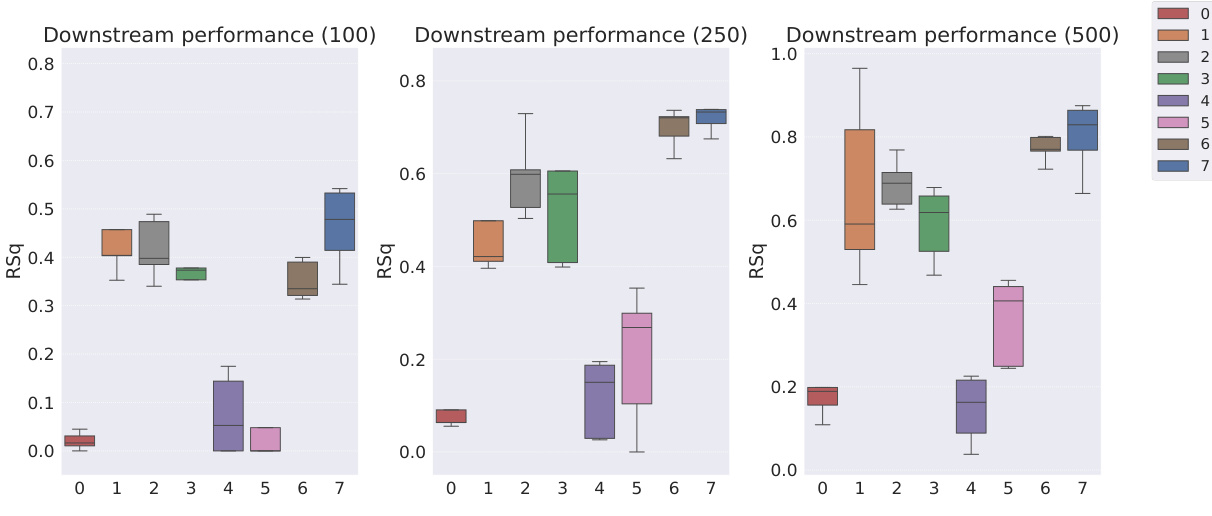
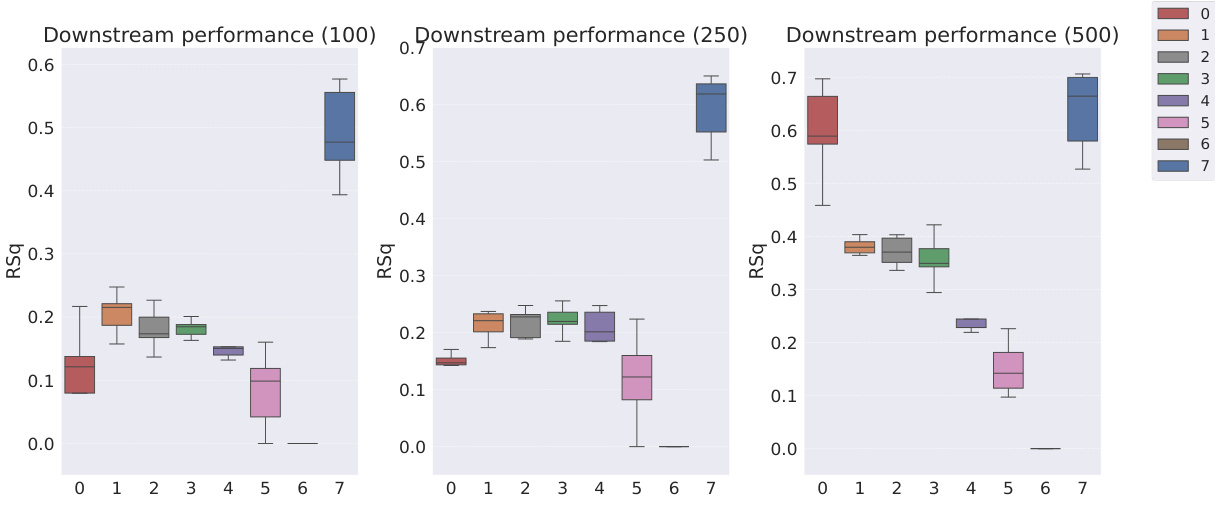
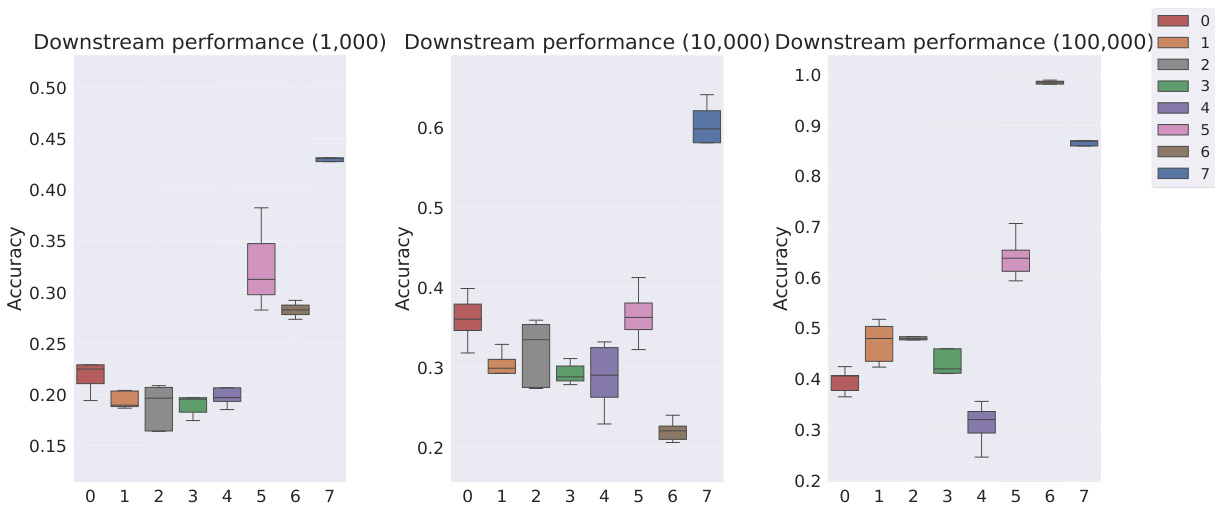
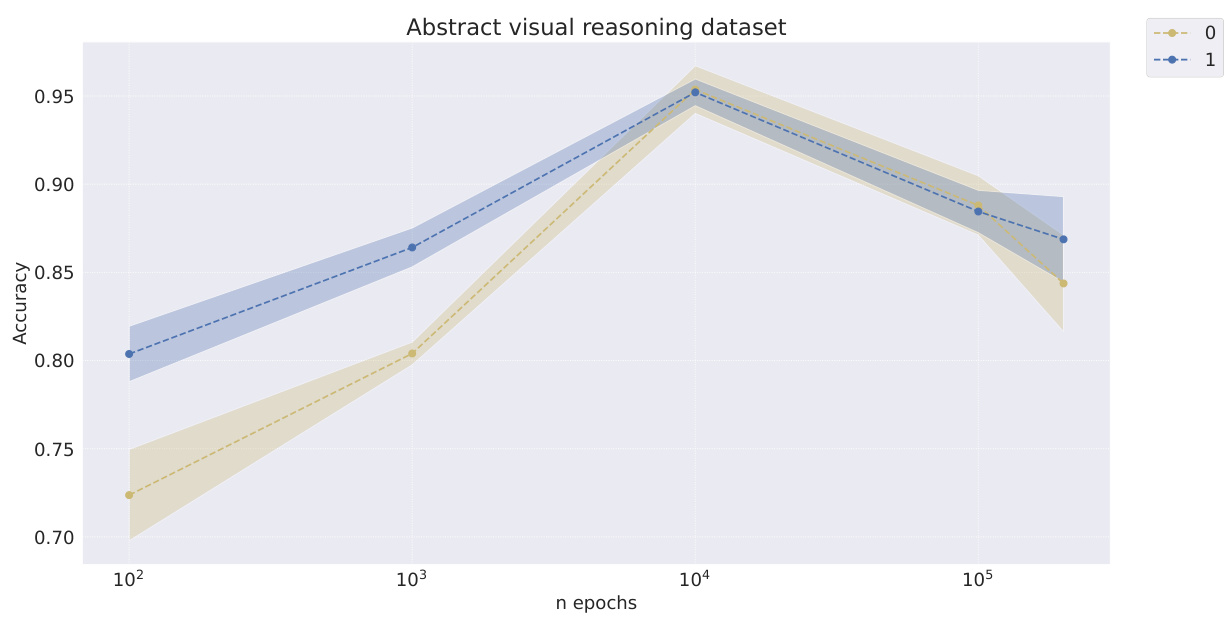
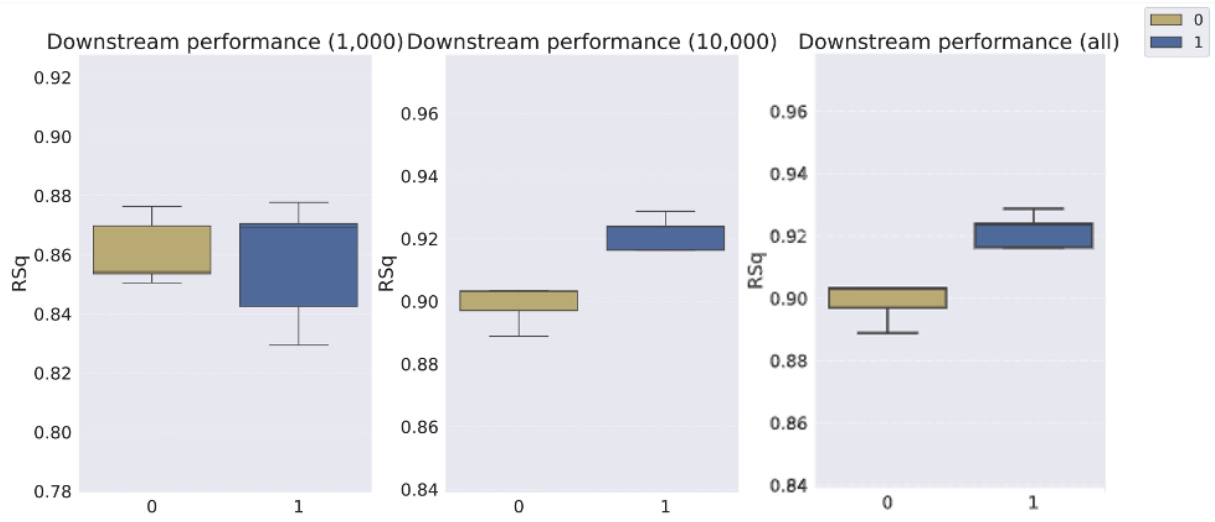
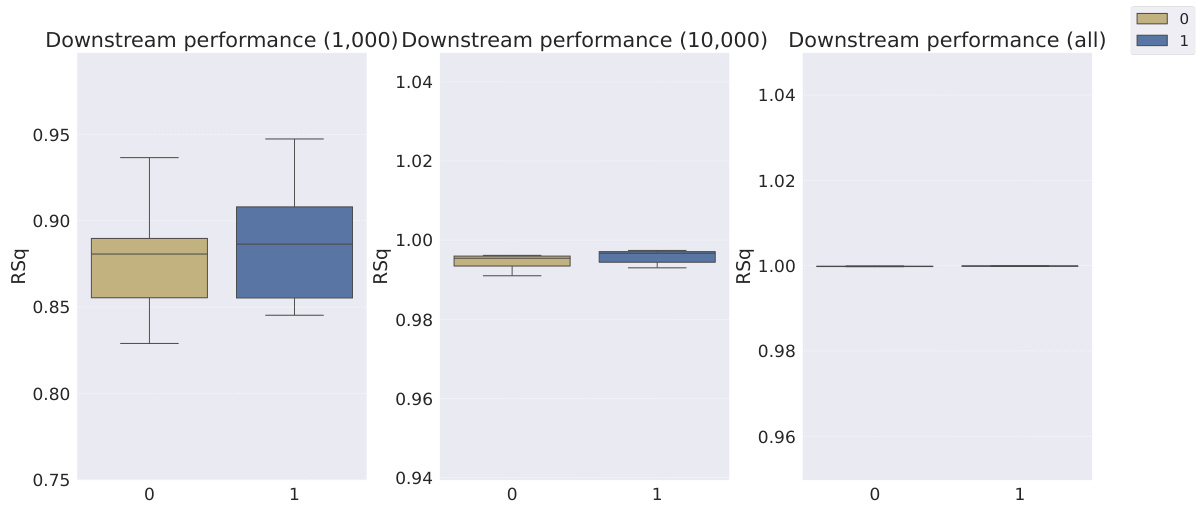
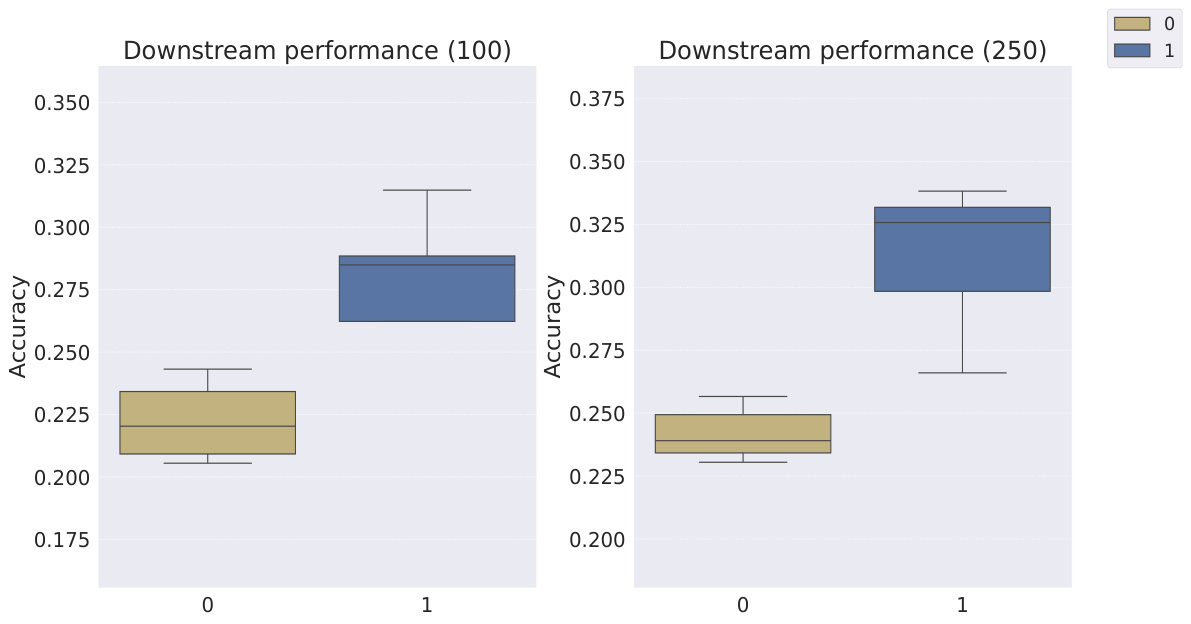
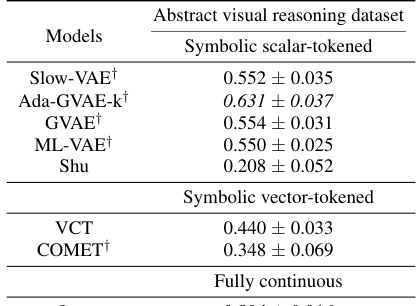
This table shows the classification accuracy of the downstream WReN model on the abstract visual reasoning dataset. The accuracy is evaluated at different stages of representation learning (100, 1000, 10000, 100000 and 200000 iterations). The table compares the performance of several models: Slow-VAE, Ada-GVAE-k, GVAE, MLVAE, Shu, VCT, COMET, and the authors’ Soft TPR model. The results are presented with standard deviations to illustrate the uncertainty of the results.
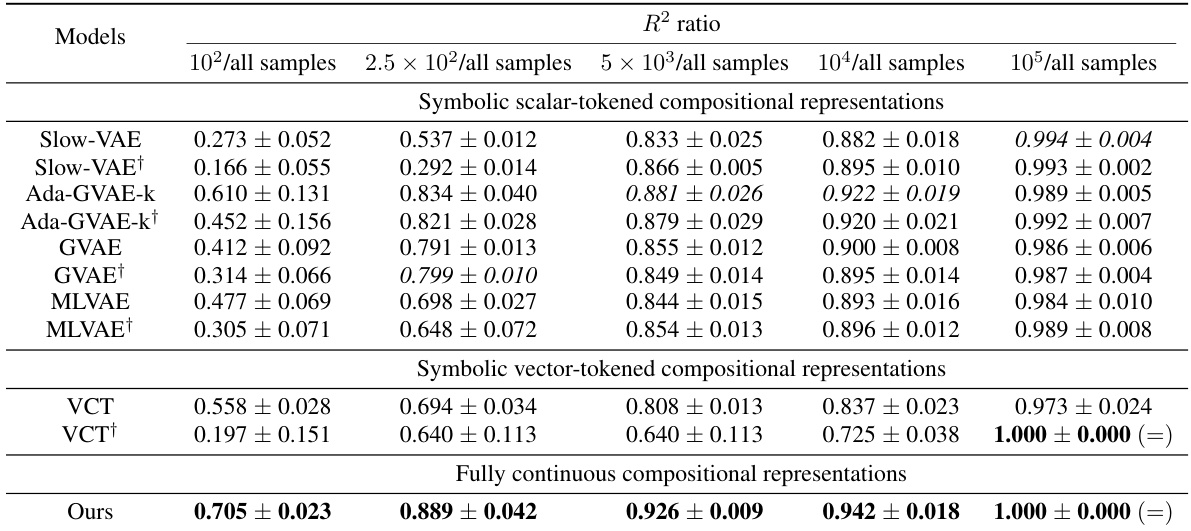
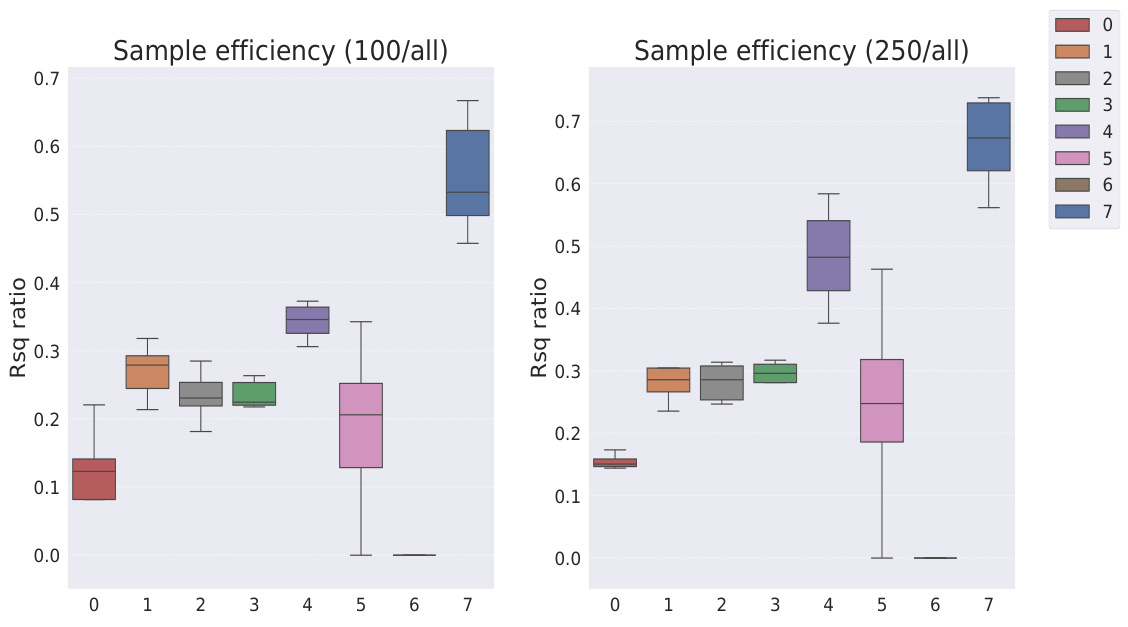
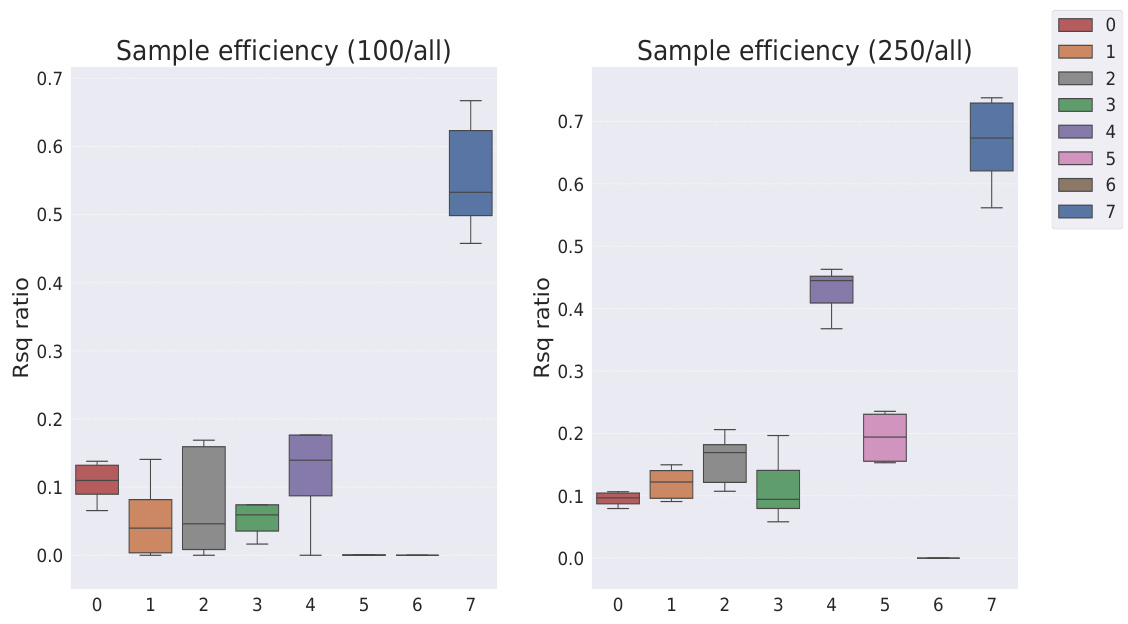
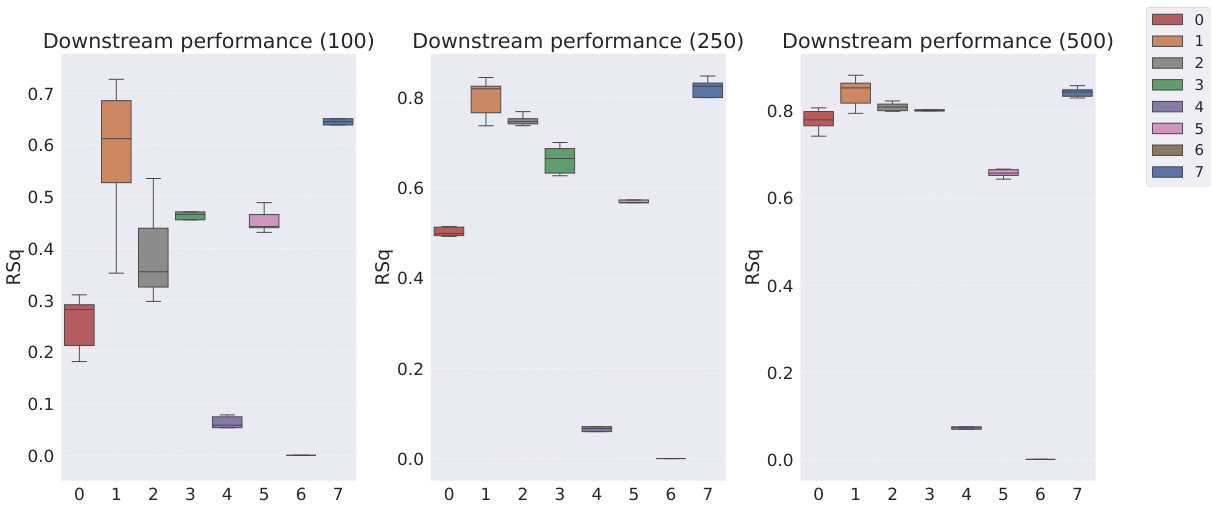
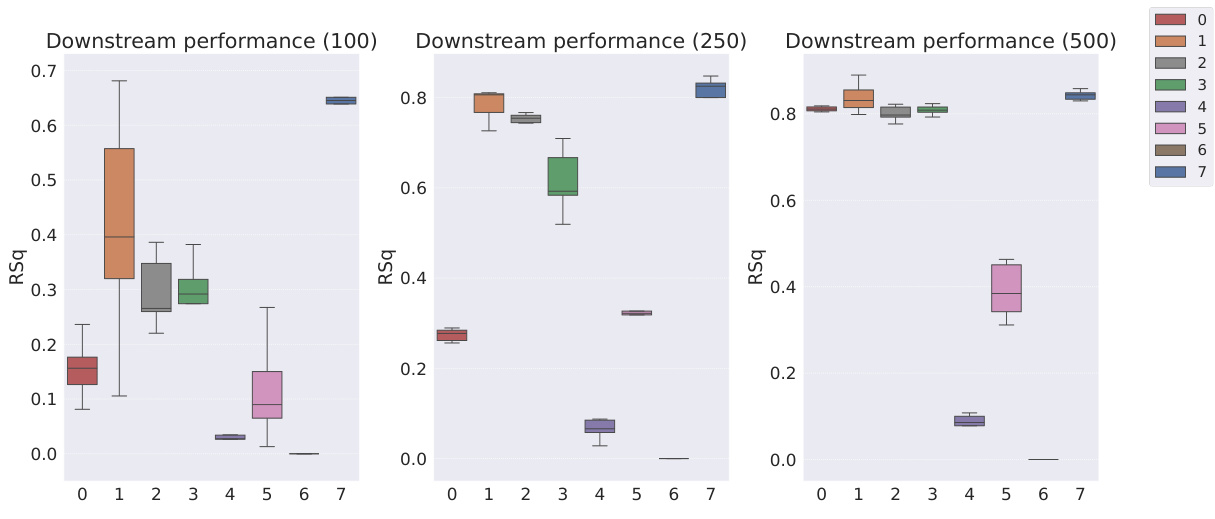
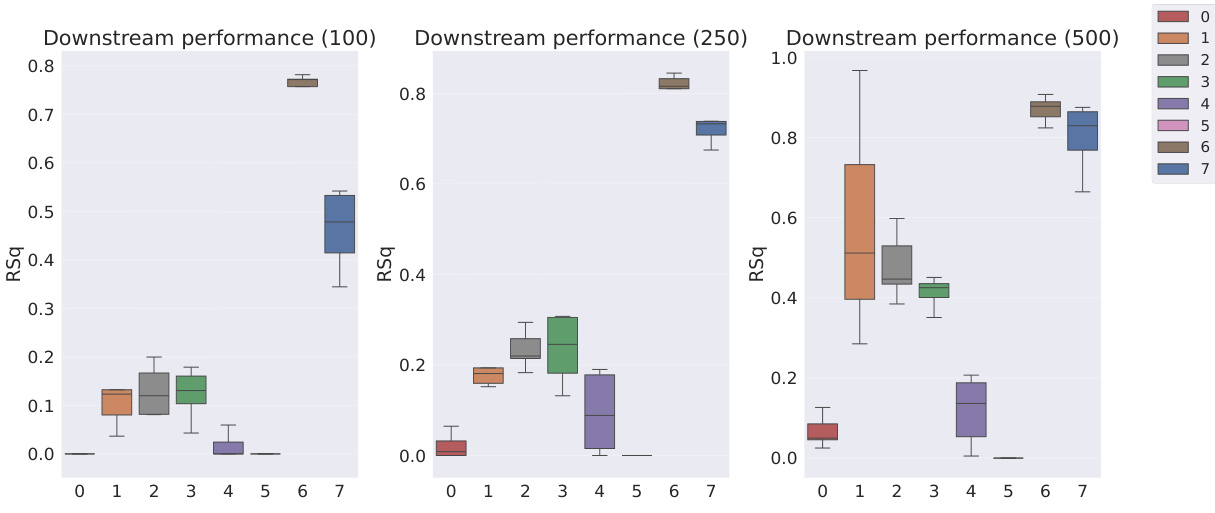
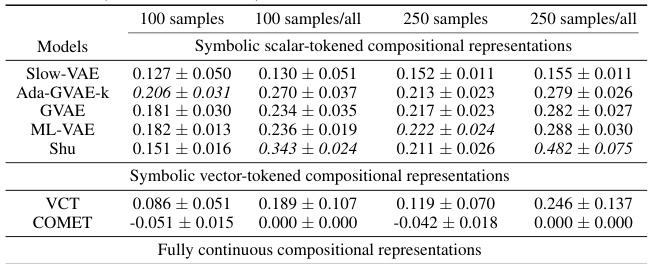
This table presents the sample efficiency results for downstream regression models trained on Cars3D dataset using different representation learning models. Sample efficiency is calculated by dividing the R-squared score of the model trained with a limited number of samples (100, 250, 500, 1000, 10000) by the R-squared score of the model trained with all available samples. The results are categorized by representation learning model type: symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representations. The table shows that the Soft TPR model generally achieves higher sample efficiency than other models, especially in low sample regimes.

This table presents the sample efficiency of downstream regression models on the Cars3D dataset. Sample efficiency is calculated by dividing the R-squared score of the model trained on a limited number of samples (100, 250, 500, 1,000, and 10,000) by the R-squared score of the model trained on all available samples. The results are shown for different representation learning methods, including symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representations. The table helps to assess how well each method performs with limited data, indicating its sample efficiency.
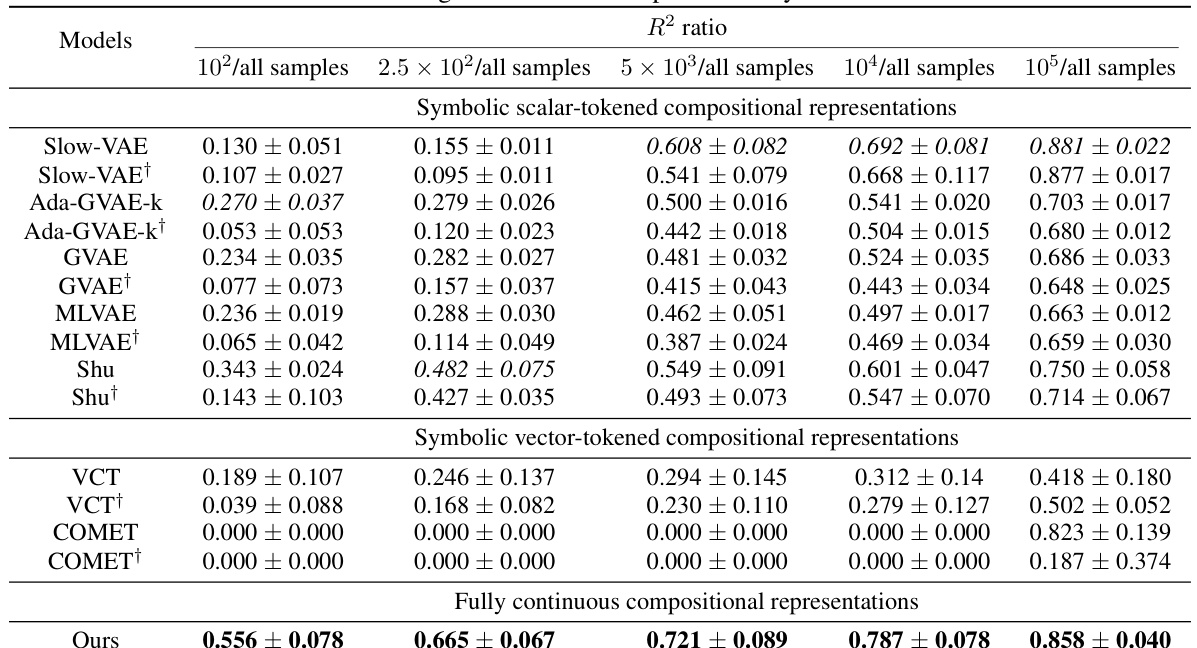
This table presents the sample efficiency results for downstream regression models on the MPI3D dataset. Sample efficiency is calculated as the ratio of the model’s performance with a limited number of samples (100, 250, 500, 1000, 10000) to its performance when trained with all samples. The results are broken down by model type (symbolic scalar-tokened, symbolic vector-tokened, fully continuous) and show the mean and standard deviation of the R2 ratio for each model and sample size.
This table presents the sample efficiency results for downstream regression models trained on Cars3D data. Sample efficiency is calculated by dividing the R-squared score of a model trained on a smaller dataset (100, 250, 500, 1000, 10000 samples) by the R-squared score of the same model trained on the full dataset. Results are presented for several models, categorized as symbolic scalar-tokened compositional representations, symbolic vector-tokened compositional representations, and fully continuous compositional representations. The table shows the mean and standard deviation for each model and sample size.

This table presents the results of downstream regression model sample efficiency on the Cars3D dataset. Sample efficiency is calculated by dividing the model’s performance when trained with a limited number of samples (100, 250, 500, 1,000, 10,000) by its performance when trained with all samples. The table shows that the Soft TPR model outperforms other models, particularly when trained on smaller datasets.

This table presents the sample efficiency results for downstream regression models trained on Cars3D dataset. Sample efficiency is calculated by dividing the R-squared score of a model trained on a limited number of samples (100, 250, 500, 1000, 10000) by the R-squared score of the same model trained on the full dataset. The table compares the sample efficiency of different models, including symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representations. The results show that Soft TPR model demonstrate superior sample efficiency compared to the other models, especially when only a small number of samples are available.
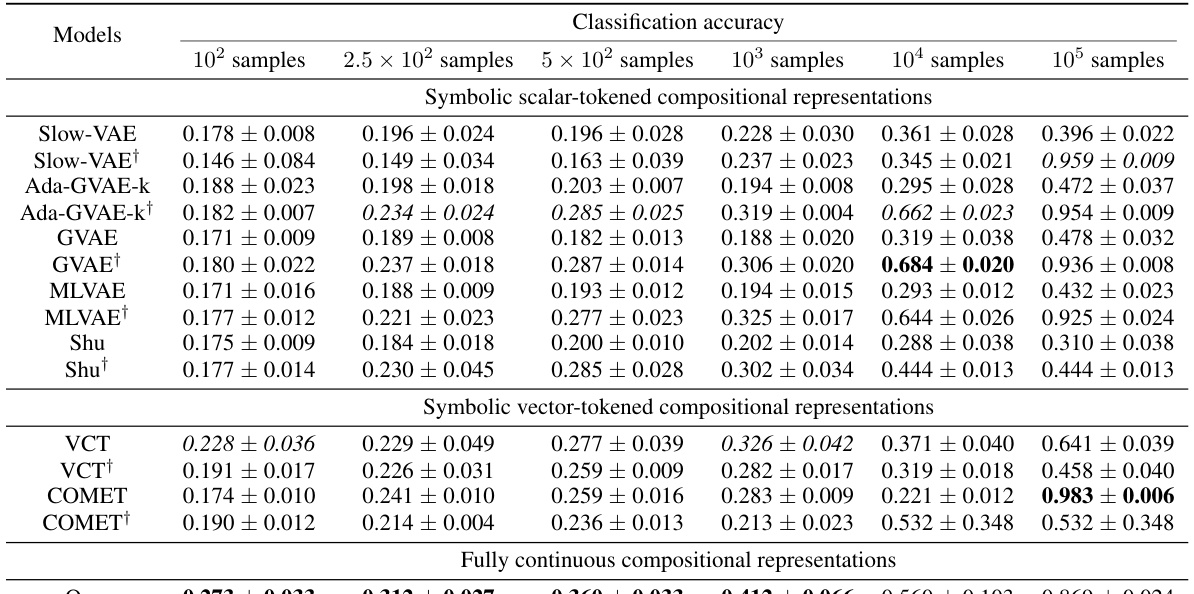
This table presents the classification accuracy results of the downstream WReN model on the abstract visual reasoning dataset for different numbers of samples used to train the representation learners. It shows how the performance of the downstream model changes as the representation learner receives more training data. The table compares various representation learning models, including the proposed Soft TPR Autoencoder, symbolic alternatives (Ada-GVAE, GVAE, MLVAE, Shu), and vector-tokened methods (VCT, COMET), highlighting the effect of the representation learning methodology on downstream model performance.

This table shows the hyperparameter values used in an ablation study on the MPI3D dataset. It includes architectural hyperparameters such as the dimensionality of the role and filler embedding spaces (DR, DF), the number of role and filler embedding vectors (NR, NF), and loss function hyperparameters such as lambda1 (λ1), lambda2 (λ2), and beta (β). The values are presented for both the original experiment and the ablation experiment.

This table presents the disentanglement metric scores obtained on the MPI3D dataset for two hyperparameter configurations: the original configuration and an ablation configuration. The metrics used are FactorVAE score, DCI score, BetaVAE score, and MIG score. The table allows for comparison of model performance across these metrics under different hyperparameter settings, providing insight into model robustness and sensitivity to hyperparameter choices.
This table presents the FactorVAE and DCI disentanglement scores for different models on the Cars3D, Shapes3D, and MPI3D datasets. The models are categorized into symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representation models. The results show the performance of each model in terms of disentanglement, where higher scores indicate better disentanglement. The Soft TPR model significantly outperforms all other baselines.
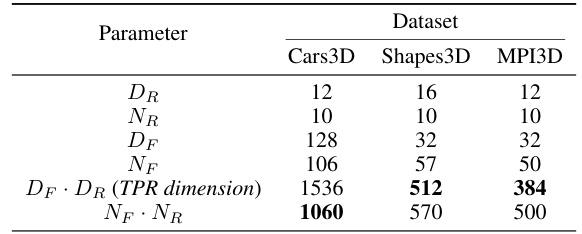
This table compares the dimensionality of the Soft TPR model with other baselines for three different datasets: Cars3D, Shapes3D, and MPI3D. It shows that while the Soft TPR model has a higher dimensionality compared to the scalar-tokened models, its dimensionality is considerably lower than the vector-tokened models (VCT and COMET), demonstrating improved scalability in relation to the number of roles (FoV types) and fillers (FoV tokens). The table highlights the trade-off between representational expressivity and computational efficiency.

This table compares the dimensionality of the representations produced by different models for the three disentanglement datasets (Cars3D, Shapes3D, MPI3D). It highlights the multiplicative growth of dimensionality in the Soft TPR approach resulting from the tensor product of role and filler embedding spaces (DR and DF). However, it also shows that the Soft TPR’s dimensionality (DF * DR) can be smaller than the total number of role-filler bindings (n) in the datasets. The table contrasts the Soft TPR’s dimensionality with those of baseline models which use either symbolic scalar-tokened or symbolic vector-tokened compositional representations.
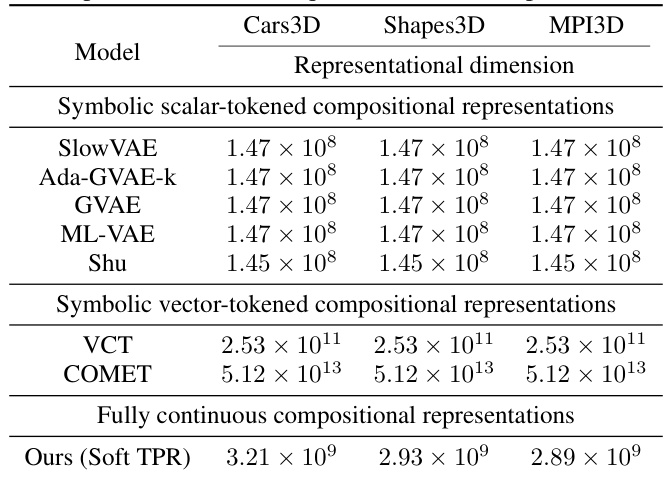
This table compares the number of floating point operations (FLOPs) required for a single forward pass of a batch size of 16 for different models. The models are categorized into symbolic scalar-tokened, symbolic vector-tokened, and fully continuous compositional representations. The FLOPs are reported for each of the three datasets used in the experiments: Cars3D, Shapes3D, and MPI3D. The table highlights the computational efficiency of the Soft TPR approach compared to the baselines.
Full paper#