TL;DR#
Bayesian Optimization (BO) is powerful but struggles with high dimensionality and large datasets due to the computational cost of Gaussian processes (GPs). Existing approximate GP methods often result in overly smooth estimations, hindering BO’s performance, especially with limited online samples. Many existing methods focus on problems with large online samples in low dimensions.
This paper introduces FOCALBO, a hierarchical BO algorithm that uses a novel focalized GP. Focalized GP improves local prediction accuracy by strategically allocating representational power to relevant search space regions. FOCALBO iteratively optimizes acquisition functions over progressively smaller search spaces, efficiently utilizing large offline and online datasets. Experiments show FOCALBO outperforms existing methods on robot morphology design and high-dimensional musculoskeletal system control, demonstrating its effectiveness in tackling real-world, large-scale optimization problems.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in Bayesian Optimization and related fields because it presents FOCALBO, a novel algorithm that efficiently handles high-dimensional problems with massive datasets. This significantly expands the applicability of BO to real-world scenarios previously deemed intractable, opening doors for further research into scaling BO for complex applications in robotics, control systems, and other domains involving large-scale datasets.
Visual Insights#
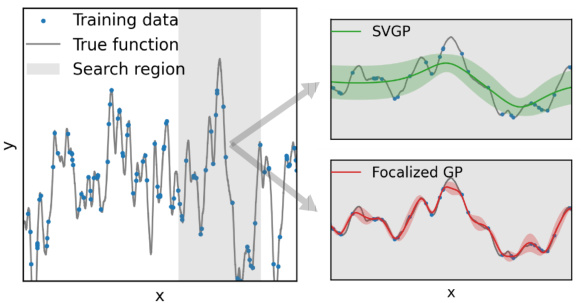
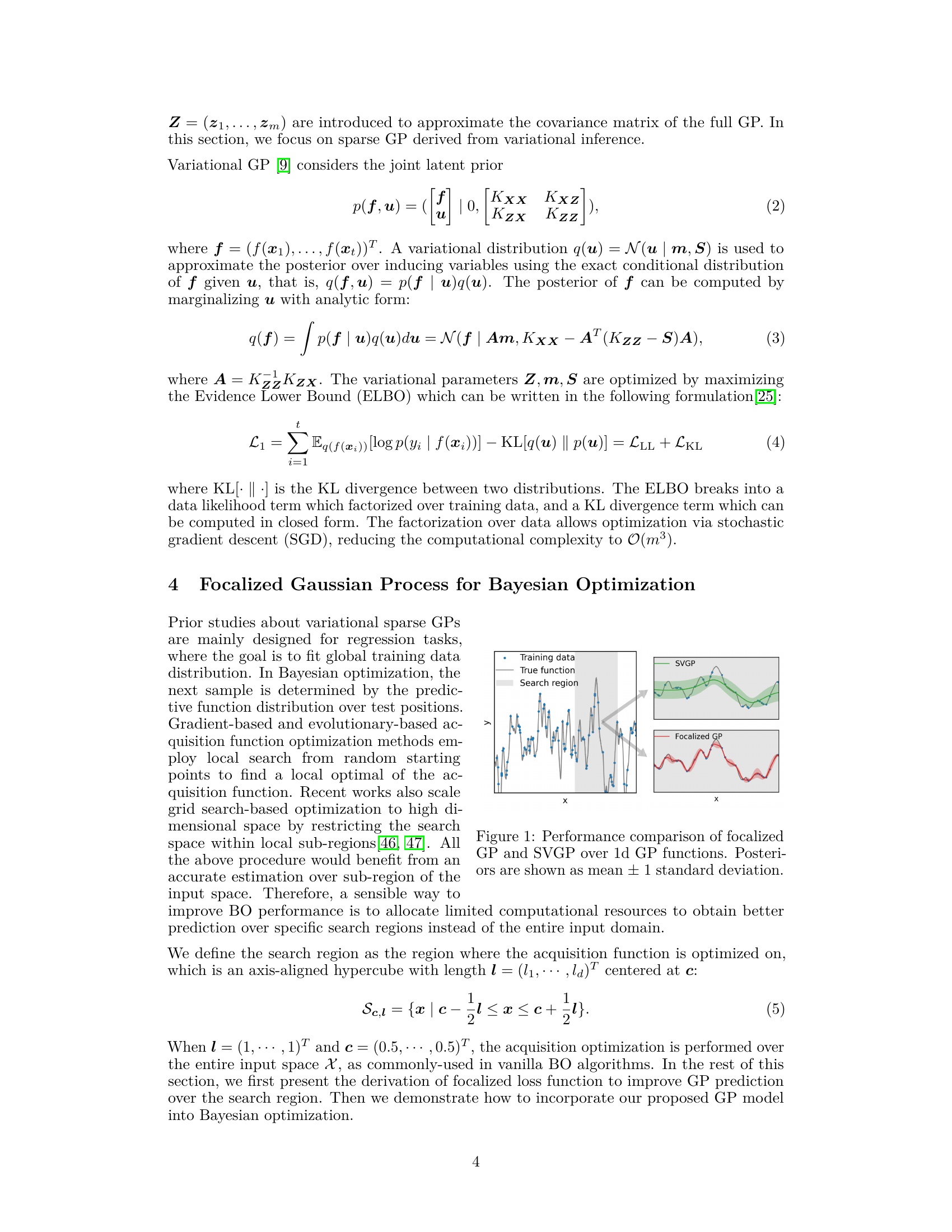
🔼 This figure compares the performance of focalized Gaussian Processes (GP) and standard Sparse Variational Gaussian Processes (SVGP) on a one-dimensional (1D) Gaussian Process function. It showcases how focalized GP, by focusing its representational power on relevant regions, produces a more accurate and localized posterior distribution compared to SVGP, which provides an overly smooth estimation across the entire function domain. The plot visually illustrates the mean and ±1 standard deviation of both models’ posterior distributions, highlighting the difference in their predictive capabilities, especially in capturing local details and uncertainties of the true underlying function.
read the caption
Figure 1: Performance comparison of focalized GP and SVGP over 1d GP functions. Posteriors are shown as mean ± 1 standard deviation.

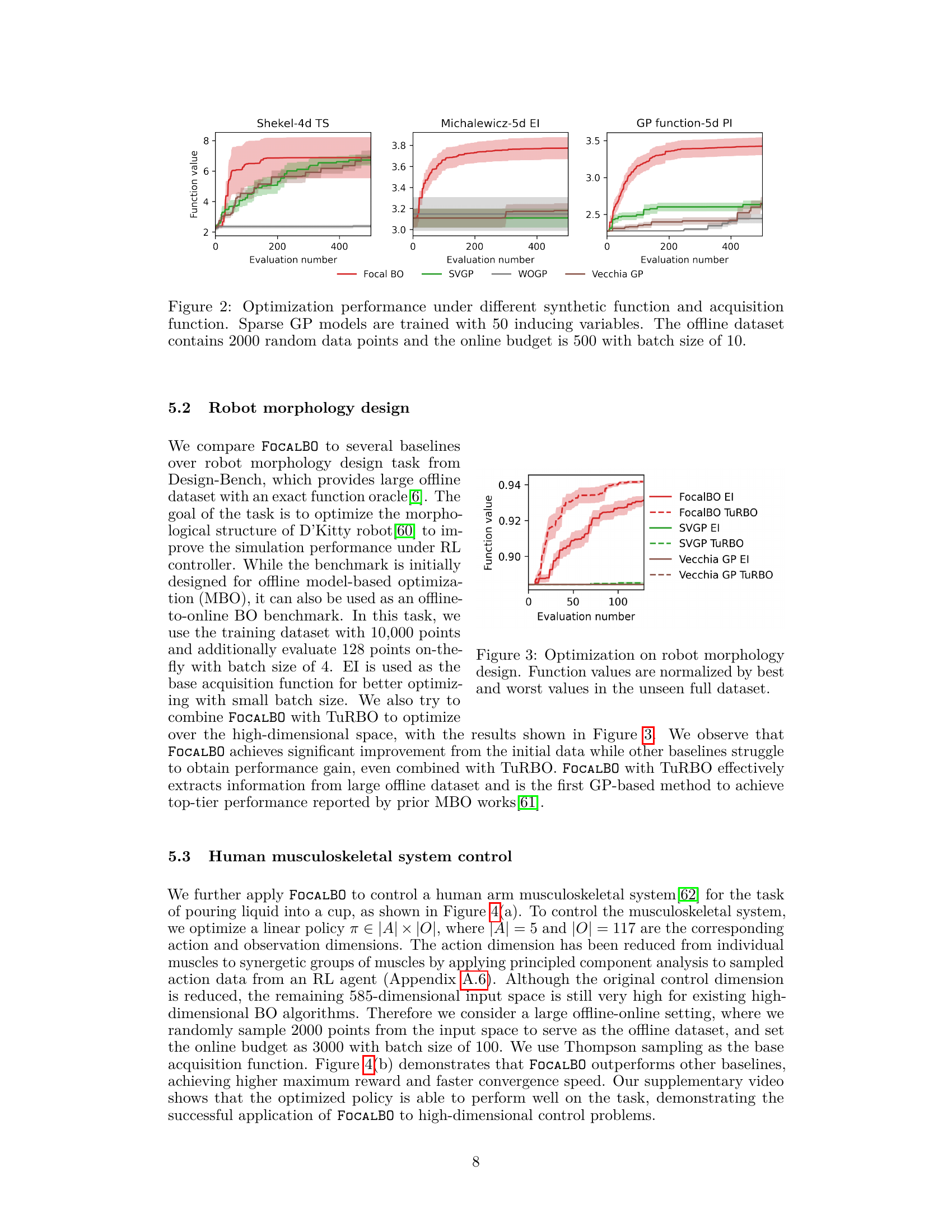
🔼 This figure compares the performance of FOCALBO against other sparse Gaussian process-based Bayesian optimization methods (SVGP, WOGP, Vecchia GP) across three different synthetic functions (Shekel, Michalewicz, and a GP function) and three different acquisition functions (TS, EI, PI). It demonstrates the superior performance of FOCALBO regardless of the acquisition function and function type. The experimental setup uses 50 inducing variables for all sparse GP models, with an offline dataset of 2000 random data points and an online budget of 500 points, evaluated in batches of 10.
read the caption
Figure 2: Optimization performance under different synthetic function and acquisition function. Sparse GP models are trained with 50 inducing variables. The offline dataset contains 2000 random data points and the online budget is 500 with batch size of 10.
In-depth insights#
Focalized GP#
The core concept of “Focalized GP” revolves around enhancing the efficiency and accuracy of sparse Gaussian Processes (GPs) within the Bayesian Optimization framework. Standard sparse GPs, while improving scalability, often suffer from overly smooth estimations due to their global perspective. Focalized GP addresses this by introducing a novel loss function that strategically focuses the model’s representational power on relevant sub-regions of the search space. This localized approach is achieved by weighting training data based on its proximity to the region of interest, thereby prioritizing the accuracy of local predictions crucial for effective acquisition function optimization. This technique allows for more efficient allocation of computational resources, leading to better performance, particularly in high-dimensional spaces and with large datasets. The effectiveness of Focalized GP is further enhanced when combined with a hierarchical optimization strategy, as demonstrated by the algorithm FOCALBO. In essence, Focalized GP offers a refined method for sparse GP training, improving both accuracy and efficiency in Bayesian optimization.
Hierarchical BO#
Hierarchical Bayesian Optimization (BO) methods address the challenge of efficiently exploring complex, high-dimensional search spaces. These methods work by recursively decomposing the search space into smaller sub-regions, allowing for focused exploration at different scales. A key advantage is the potential for improved efficiency, as resources are concentrated on promising areas. Early stages might explore broadly using global models, then refining the search using local models in increasingly specific areas. This approach is particularly beneficial for problems with multimodal objective functions or where there’s a high degree of heterogeneity across the search space. However, careful design is crucial. Challenges include selecting appropriate sub-region divisions, managing the interactions between different levels of the hierarchy, and balancing exploration and exploitation effectively at each level. The effectiveness also depends on the choice of surrogate models and acquisition functions used for each level; poorly chosen methods at any level can hinder overall performance. A successful hierarchical BO method requires a sophisticated interplay between global and local optimization strategies.
High-D Optimization#
High-dimensional optimization (High-D Optimization) presents unique challenges due to the curse of dimensionality, where the search space expands exponentially with the number of dimensions. Traditional methods often fail to scale effectively. The paper explores sparse Gaussian processes as a surrogate model to address this, focusing on efficiently allocating representational power to relevant regions. The hierarchical optimization strategy of FOCALBO, which iteratively refines the search space, shows promise in efficiently handling both large offline and online datasets. This approach is particularly effective when dealing with heterogeneous functions, demonstrating state-of-the-art results in complex domains like robot morphology design and musculoskeletal system control. The combination of focalized GP for better local prediction and the hierarchical approach of FOCALBO offers a powerful strategy for tackling High-D Optimization problems, showcasing its capability for solving complex, real-world challenges.
Offline Data Use#
The effective use of offline data is a crucial, yet often underexplored, aspect of Bayesian Optimization (BO). Many BO algorithms focus primarily on online data acquisition, neglecting the potential value of pre-existing datasets. Leveraging offline data can significantly reduce the number of expensive online evaluations needed, especially when dealing with high-dimensional or computationally intensive problems. A well-designed BO method should seamlessly integrate offline data to improve the surrogate model’s accuracy and reduce uncertainty. This might involve techniques like carefully weighting offline data based on relevance to the current search area, perhaps by proximity to promising regions identified in earlier iterations. Strategies for handling the potential heterogeneity and noise levels in offline data are also vital. Techniques such as robust regression methods or clustering could improve the reliability of the surrogate model. Furthermore, the computational cost of incorporating large offline datasets must be considered; scalable methods like sparse Gaussian processes are essential for efficient handling of massive offline data, but also need to avoid overly-smoothing the surrogate model’s estimation of the objective function. In summary, a robust BO system should be capable of efficiently utilizing offline data to enhance performance, focusing on intelligent data selection, robust modeling, and computationally efficient algorithms.
Future Research#
Future research directions stemming from this work on scalable Bayesian Optimization (BO) using focalized sparse Gaussian processes could explore several avenues. Improving the theoretical understanding of FOCALBO’s regret bounds and convergence properties is crucial. This involves a deeper analysis of the proposed focalized ELBO loss function and its impact on the approximation quality of sparse GPs in high-dimensional spaces. Developing more sophisticated acquisition functions optimized within the hierarchical framework of FOCALBO could further enhance its efficiency. Investigating alternative methods for selecting inducing points or employing other sparse GP formulations may lead to more robust and scalable algorithms. Extending FOCALBO to handle constraints or different types of optimization problems is another significant area for future work. Finally, applying FOCALBO to a broader range of real-world applications beyond robot control and musculoskeletal system design, such as hyperparameter tuning in deep learning or materials science, would demonstrate its generalizability and impact.
More visual insights#
More on figures

🔼 This figure compares the performance of Focal BO against other sparse Gaussian process (GP) models (SVGP, WOGP, Vecchia GP) across three different acquisition functions (TS, EI, PI) and three different synthetic functions (Shekel, Michalewicz, GP function). Each function is optimized using the selected acquisition function. The offline dataset used for training is 2000 random data points and an additional 500 points are sampled online during optimization in batches of size 10. The figure shows that FOCALBO significantly outperforms the baselines in most cases.
read the caption
Figure 2: Optimization performance under different synthetic function and acquisition function. Sparse GP models are trained with 50 inducing variables. The offline dataset contains 2000 random data points and the online budget is 500 with batch size of 10.
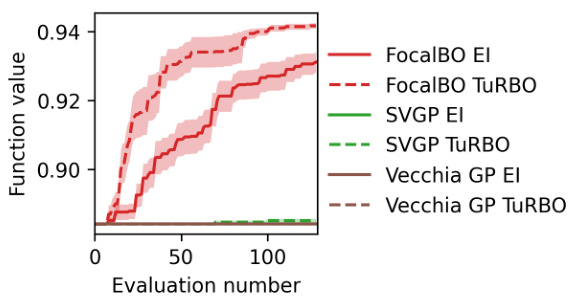
🔼 The figure compares the optimization performance of FOCALBO with other baselines (SVGP, Vecchia GP) on a robot morphology design task. Both EI and TuRBO acquisition functions are used for each baseline. The y-axis represents the normalized function value (best and worst values from the unseen full dataset are used for normalization), and the x-axis represents the number of function evaluations. The plot shows that FOCALBO achieves significantly better results than the other methods, demonstrating its effectiveness in this high-dimensional problem.
read the caption
Figure 3: Optimization on robot morphology design. Function values are normalized by best and worst values in the unseen full dataset.

🔼 This figure demonstrates the application of the proposed FOCALBO algorithm to a musculoskeletal system control task. Subfigure (a) shows a visual representation of the task, illustrating the initial and final states of the system. Subfigure (b) presents a comparison of FOCALBO’s performance against several baseline algorithms in terms of optimization performance. The plot shows how the objective function value changes over the course of the optimization process, allowing us to compare the algorithms’ efficiency and effectiveness in reaching an optimal solution. The shaded region represents the variance between different optimization runs. The full video of the task is available in supplementary materials.
read the caption
Figure 4: Optimization of musculoskeletal system control. (a) Task illustration of initial and target state. Full video in supplementary. (b) Optimization performance of algorithms.
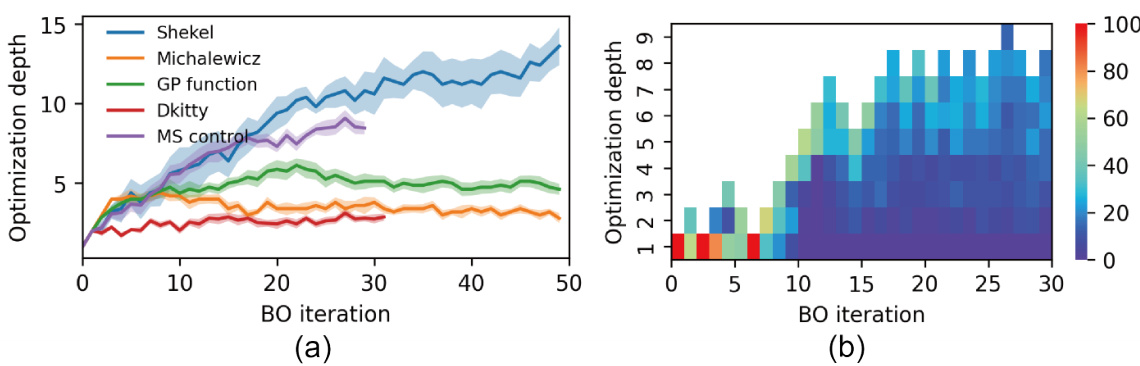
🔼 This figure analyzes the optimization depth used in FOCALBO, a hierarchical Bayesian optimization algorithm. Panel (a) shows how the optimization depth changes over several BO iterations for different problem types (Shekel, Michalewicz, GP function, DKitty robot morphology design, and musculoskeletal system control). The lines show the average optimization depth and the shaded areas represent standard deviations. Panel (b) is a heatmap showing the source of the sampled batches used in each BO iteration during the musculoskeletal system control optimization task. The color intensity represents the number of samples obtained at each depth. The figure demonstrates that FOCALBO’s adaptive strategy allows for a dynamic balance between exploration and exploitation.
read the caption
Figure 5: Algorithm analysis over optimization depth. (a) Depth evolution during optimization. (b) Samples source of each BO iteration during one trial of musculoskeletal system control optimization. Color bar indicates the number of samples proposed by corresponding optimization depth.
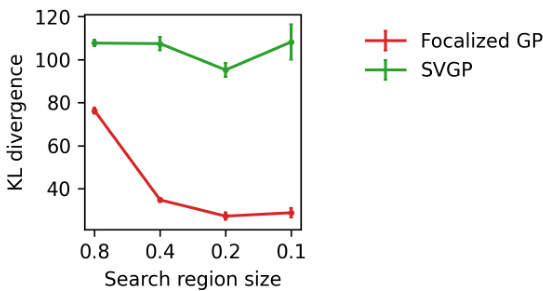
🔼 This figure compares the KL divergence between the posterior distributions of focalized GP and SVGP against the exact GP’s posterior distribution. The KL divergence quantifies the difference between probability distributions; a lower KL divergence indicates a better approximation. The figure shows that the focalized GP consistently achieves a lower KL divergence than SVGP across various sizes of the search region, demonstrating that it provides a closer approximation to the true posterior distribution, especially in smaller search regions.
read the caption
Figure 6: KL divergence between sparse GPs and exact GP. Results shows the mean and one standard error, averaged over 50 independent trials.
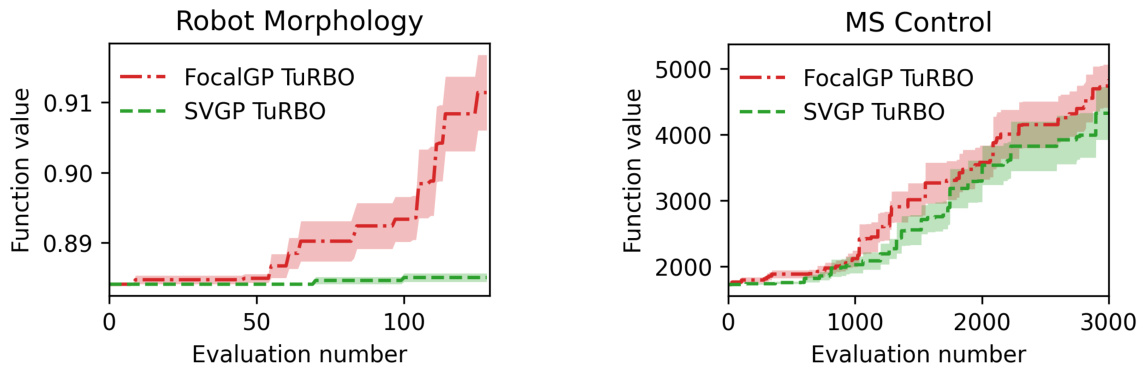
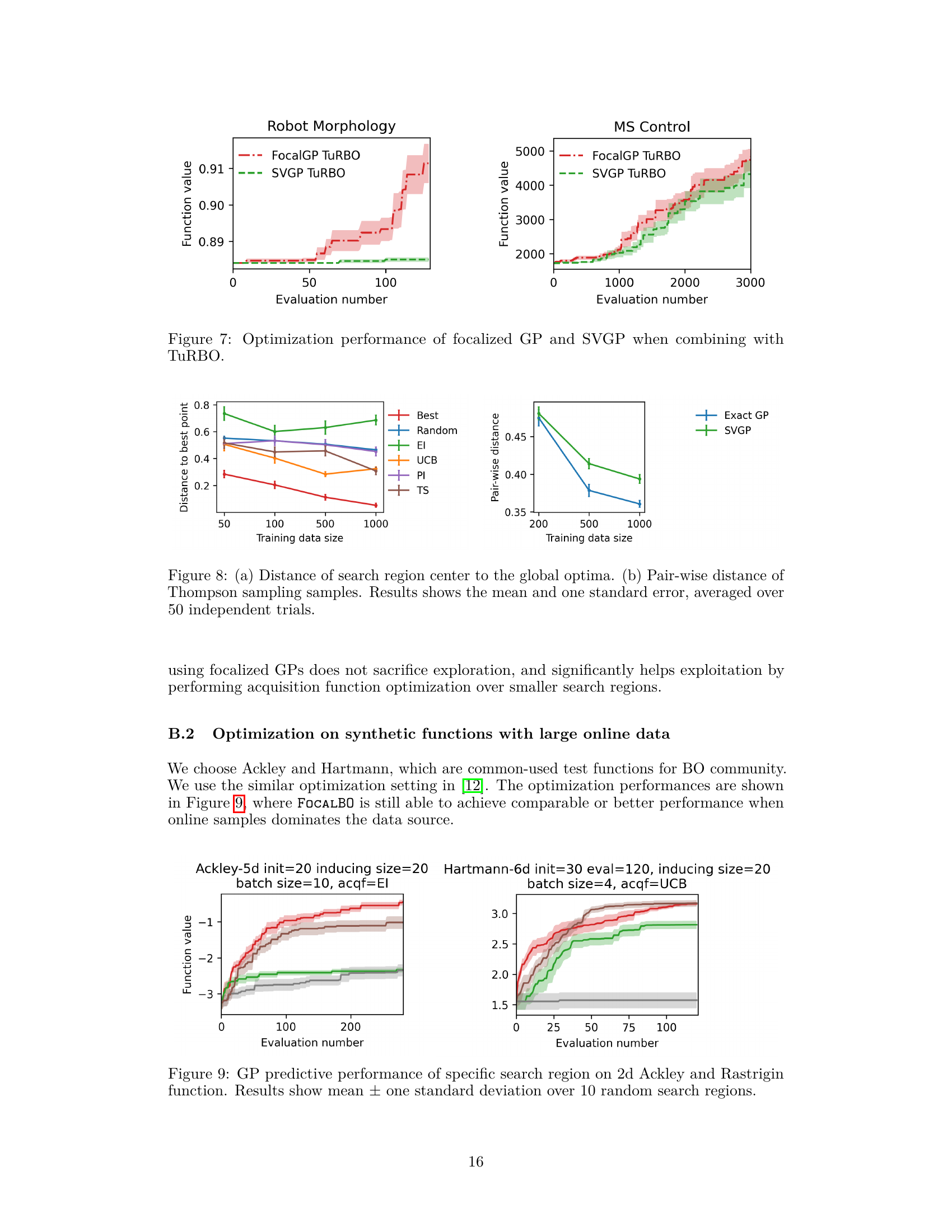
🔼 The figure compares the optimization performance of focalized GP and SVGP when combined with TuRBO on two tasks: robot morphology design and musculoskeletal system control. It shows that FocalGP consistently outperforms SVGP across both tasks. The shaded area represents the standard error of the mean.
read the caption
Figure 7: Optimization performance of focalized GP and SVGP when combining with TURBO.
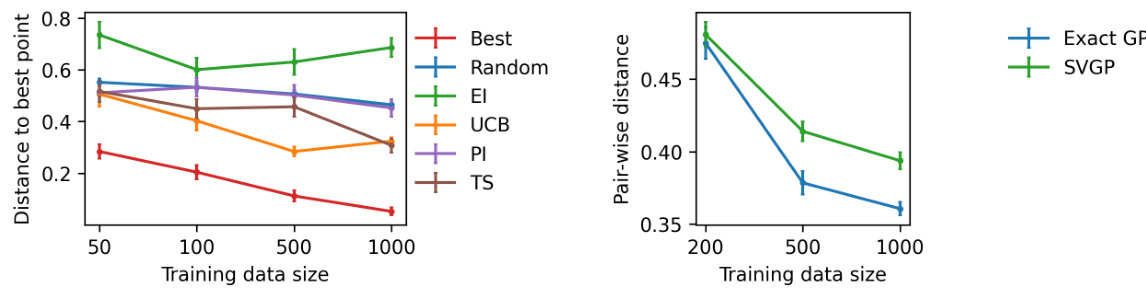
🔼 This figure contains two subfigures. Subfigure (a) shows the distance between the center of the search region used in the FOCALBO algorithm and the global optimum for various acquisition functions (Best, Random, EI, UCB, PI, TS) and training data sizes (50, 100, 500, 1000). It demonstrates how well the algorithm centers the search region around the global optimum. Subfigure (b) displays the average pairwise distance of Thompson sampling points for exact GP and SVGP (with 50 inducing points) across different training data sizes (200, 500, 1000). This illustrates the exploration-exploitation trade-off; how sparse GPs encourage more exploration by sampling diverse points compared to using the full GP.
read the caption
Figure 8: (a) Distance of search region center to the global optima. (b) Pair-wise distance of Thompson sampling samples. Results shows the mean and one standard error, averaged over 50 independent trials.
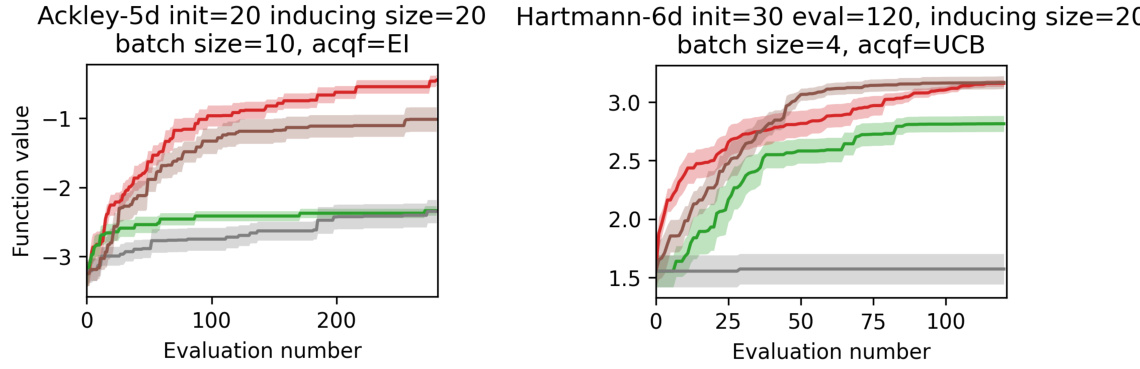
🔼 This figure compares the performance of different GP models (FocalBO, SVGP, and WOGP) on two benchmark functions, Ackley and Hartmann. The optimization is performed in a setting with a large amount of online data. Results show that FOCALBO consistently outperforms baselines in both functions, suggesting its effectiveness in online optimization scenarios when online data becomes dominant.
read the caption
Figure 9: GP predictive performance of specific search region on 2d Ackley and Rastrigin function. Results show mean ± one standard deviation over 10 random search regions.
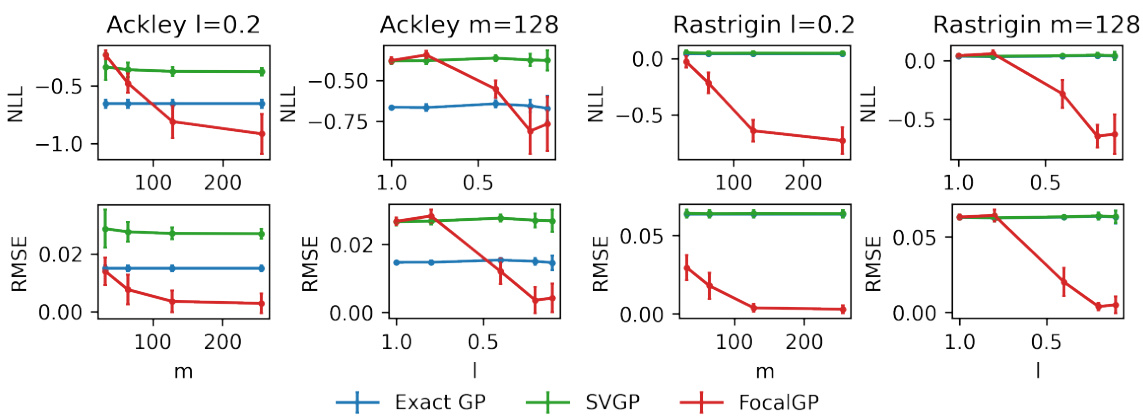
🔼 This figure displays the results of a comparison of the predictive performance of three different Gaussian process (GP) models: Exact GP, SVGP, and FocalGP. The comparison is done across varying search region sizes (l) and different numbers of inducing variables (m) on two benchmark functions: Ackley and Rastrigin. The performance is measured using two metrics: negative log-likelihood (NLL) and root mean squared error (RMSE). The error bars represent the standard deviation across 10 random trials for each configuration. The figure aims to demonstrate the effectiveness of the FocalGP model, particularly in smaller search regions, by showing its superior predictive accuracy compared to the other two models.
read the caption
Figure 10: GP predictive performance of specific search region on 2d Ackley and Rastrigin function. Results show mean ± one standard deviation over 10 random search regions.
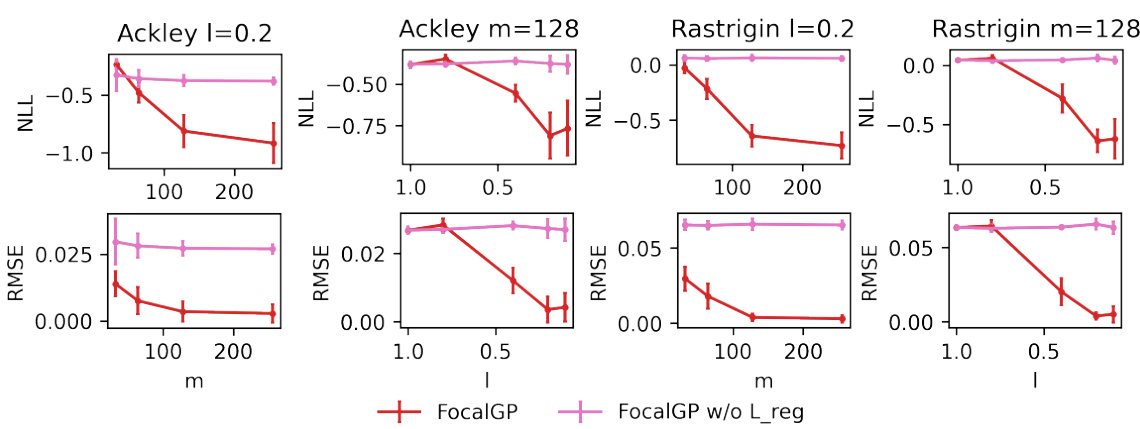
🔼 This figure compares the performance of Focalized GP, Focalized GP without regularization (Lreg), and Exact GP in terms of negative log-likelihood (NLL) and root mean squared error (RMSE) on Ackley and Rastrigin functions. The comparison is done for various search region sizes (l) and different numbers of inducing points (m). It demonstrates that Focalized GP with regularization significantly outperforms others, especially in smaller search regions, highlighting its effectiveness in improving local prediction accuracy.
read the caption
Figure 10: GP predictive performance of specific search region on 2d Ackley and Rastrigin function. Results show mean ± one standard deviation over 10 random search regions.
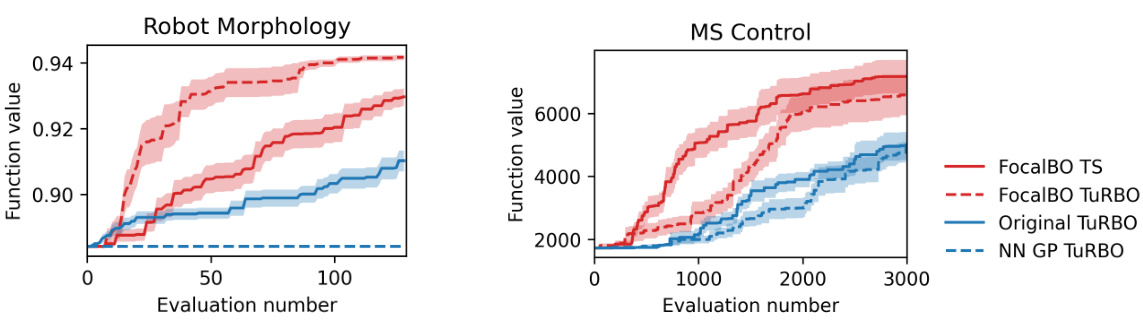
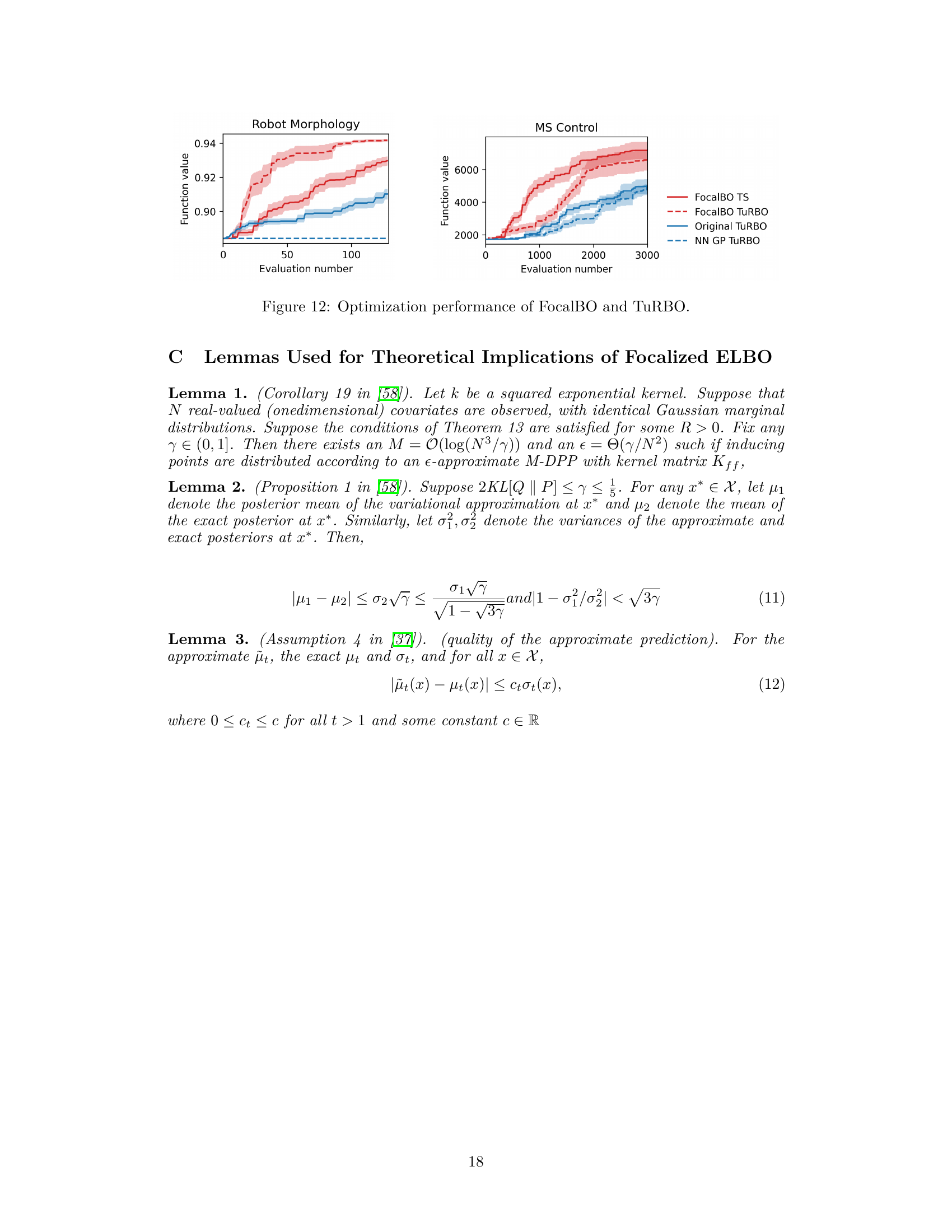
🔼 This figure compares the optimization performance of FocalBO and TuRBO on two tasks: Robot Morphology and MS Control. For each task, it shows the optimization progress for four methods: FocalBO using Thompson Sampling (TS), FocalBO combined with TuRBO, the original TuRBO method, and TuRBO using a nearest neighbor Gaussian process (NN GP). The shaded areas represent the standard error for each method across multiple trials. The results demonstrate that FocalBO outperforms TuRBO on both tasks, suggesting the effectiveness of the hierarchical acquisition optimization strategy and the focalized Gaussian process in improving BO performance.
read the caption
Figure 12: Optimization performance of FocalBO and TuRBO.
Full paper#