TL;DR#
Offline reinforcement learning often struggles with distributional shift, leading to poor performance due to overestimated action values. Current methods using pessimistic value iteration address this by penalizing rewards based on the uncertainty of predicted next states, usually estimated via Monte Carlo sampling; however, this randomness significantly slows convergence.
This paper introduces Moment Matching Offline Model-Based Policy Optimization (MOMBO), which uses progressive moment matching to deterministically propagate uncertainty. MOMBO approximates next-state distributions with a normal distribution, and this deterministic propagation is computationally cheaper, allowing for faster convergence and tighter suboptimality bounds. Empirical results confirm MOMBO’s speed and comparable asymptotic performance to sampling-based methods across benchmark tasks.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in offline reinforcement learning as it directly addresses the limitations of current uncertainty-based methods. By introducing a deterministic approach using moment matching, MOMBO significantly accelerates convergence speed and provides stronger suboptimality guarantees. This work opens up new avenues for improving the efficiency and reliability of offline RL algorithms, especially in safety-critical applications where sample efficiency is paramount.
Visual Insights#

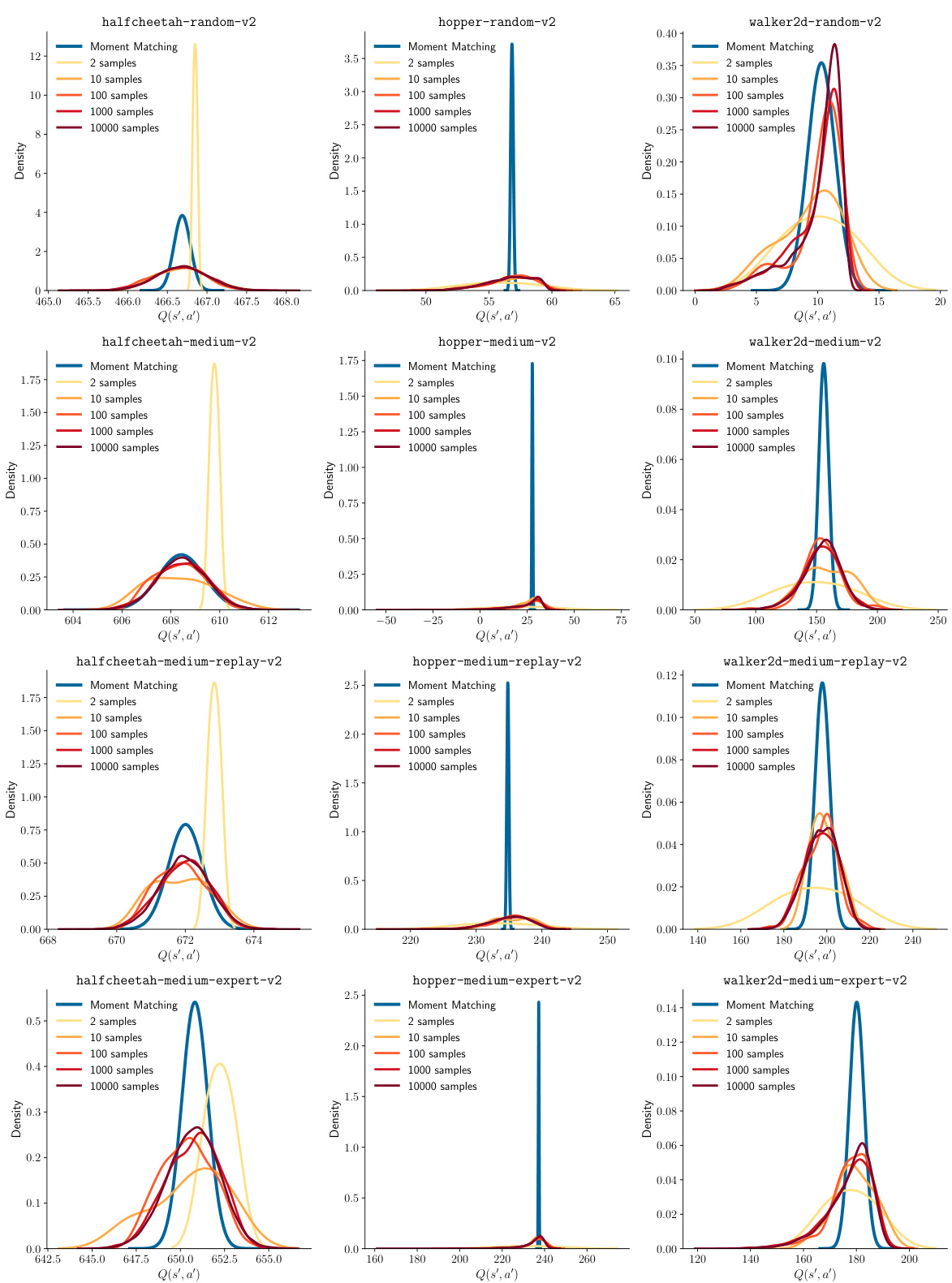
🔼 The figure compares the distribution of Q(s’,a’) estimations using moment matching and Monte Carlo sampling with varying sample counts. Moment matching provides a sharper, more accurate estimate with only two samples, significantly outperforming Monte Carlo sampling even with 10000 samples.
read the caption
Figure 1: Moment Matching versus Monte Carlo Sampling. Moment matching offers sharp estimates of the action-value of the next state at the cost of only two forward passes through a critic network. A similar sharpness cannot be reached even with 10000 Monte Carlo samples, which is 5000 times more costly. See Appendix C.1.1 for details.
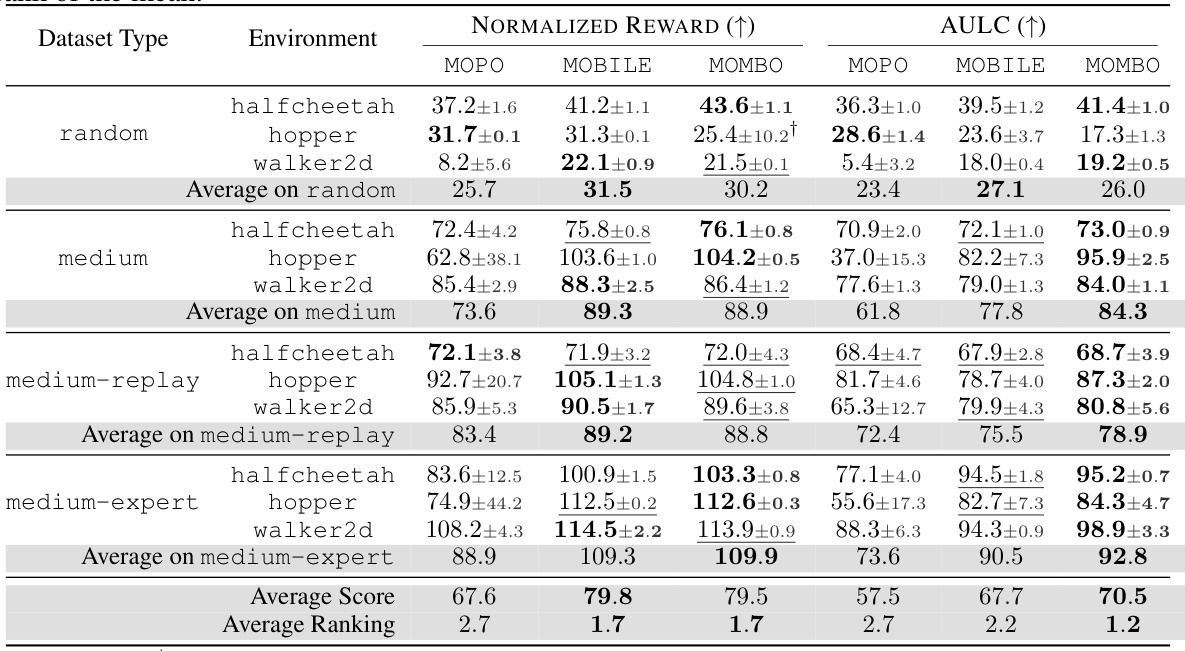
🔼 This table presents the performance of three offline reinforcement learning algorithms (MOPO, MOBILE, and MOMBO) on the D4RL dataset. The performance is measured using two metrics: Normalized Reward (the total episode reward, normalized by random and expert policies) and Area Under the Learning Curve (AULC, measuring learning speed). The results are averaged across four repetitions for each of twelve tasks, with the best results highlighted. The table also includes average scores and rankings across all tasks.
read the caption
Table 1: Performance evaluation on the D4RL dataset. Normalized reward at 3M gradient steps and Area Under the Learning Curve (AULC) (mean±std) scores are averaged across four repetitions for the MuJoCo domain of the D4RL offline reinforcement learning dataset. The highest means are highlighted in bold and are underlined if they fall within one standard deviation of the best score. The average normalized score is the average across all tasks. The average ranking is based on the rank of the mean.
In-depth insights#
Offline RL Shift#
Offline reinforcement learning (RL) grapples with the challenge of distributional shift, where the data used for training differs significantly from the data encountered during deployment. This is a critical limitation because offline RL algorithms learn from a fixed dataset, collected typically by a behavior policy, which may not adequately represent the state-action space explored by the learned policy. The resulting performance discrepancy highlights the critical need to mitigate distributional shift. Approaches to address this often involve techniques such as pessimistic value iteration, which incorporates uncertainty to constrain the policy search within the data distribution. However, the effectiveness of these methods often hinges on accurate uncertainty estimation, which can be computationally expensive and prone to sampling errors. Successfully addressing offline RL shift requires a balance between effective exploration of the state-action space and robust policy learning within the boundaries of the training data. Novel approaches will likely continue to explore deterministic methods and improved uncertainty modeling to enhance efficiency and reduce sensitivity to sampling noise.
PEVI Limitations#
Pessimistic Value Iteration (PEVI) methods, while theoretically sound for addressing distributional shift in offline reinforcement learning, suffer from practical limitations. Monte Carlo sampling, a common approach for estimating the Bellman target’s uncertainty, introduces significant randomness, slowing convergence and hindering performance. This randomness stems from the difficulty of accurately calculating the variance of deep neural network outputs, leading to high-variance estimates for reward penalization. The resulting suboptimality guarantees are often loose, and the randomness prevents efficient convergence. Furthermore, deep neural network approximations make calculating the variance analytically intractable, leading to reliance on computationally expensive Monte Carlo methods. Approaches which attempt to overcome these issues usually introduce heuristics, making the theoretical guarantees less reliable. Therefore, more deterministic and efficient approaches, such as moment matching, are needed to fully harness the potential of PEVI.
MOMBO Algorithm#
The MOMBO algorithm, short for Moment Matching Offline Model-Based Policy Optimization, presents a novel approach to offline reinforcement learning. Its core innovation lies in replacing the stochastic Monte Carlo sampling in traditional pessimistic value iteration with a deterministic moment-matching technique. This deterministic approach significantly accelerates convergence and enhances the efficiency of uncertainty propagation, crucial aspects in offline RL due to limited data and potential distributional shifts. By approximating hidden layer activations with a normal distribution, MOMBO enables a more precise and efficient computation of uncertainty, resulting in tighter suboptimality guarantees compared to sampling-based methods. This deterministic uncertainty propagation leads to faster convergence during training and improved asymptotic performance. The algorithm’s theoretical underpinnings are thoroughly investigated, providing strong analytical bounds on suboptimality, further solidifying its advantages. Overall, MOMBO offers a compelling improvement over existing offline reinforcement learning approaches by addressing the inherent limitations of Monte Carlo sampling and providing both theoretical and empirical support for its superior performance.
Uncertainty Quant.#
In the realm of offline reinforcement learning, accurately quantifying uncertainty is crucial for effective policy optimization. Uncertainty quantification methods aim to estimate the confidence in predicted rewards and next states, addressing the inherent challenges of distributional shift in offline data. Pessimistic value iteration approaches often employ uncertainty quantification to penalize riskier actions and encourage more conservative policies. However, these methods often rely on Monte Carlo sampling, which introduces significant randomness, impacting convergence and efficiency. Deterministic uncertainty propagation, as explored in the paper, offers a promising alternative. By using techniques like moment matching, these methods aim to reduce computational cost and improve the stability and speed of the learning process. The key trade-off lies in balancing the accuracy and efficiency of uncertainty estimation. While deterministic methods can be computationally more efficient, they might compromise on the precision of the uncertainty estimates. The optimal approach would depend on the specific application and the balance between computational cost and accuracy desired.
Future Works#
The paper’s core contribution is a novel deterministic method for uncertainty propagation in offline reinforcement learning, improving the efficiency and performance of model-based approaches. Future work could explore several promising avenues. One is to extend the moment-matching technique beyond ReLU activations, enhancing its applicability to various neural network architectures. Another involves investigating the method’s robustness when dealing with non-Gaussian noise or more complex environment models. A key area for investigation would be to develop tighter theoretical guarantees, potentially moving beyond the current suboptimality bounds. Further empirical evaluation across a wider range of benchmark tasks and real-world applications is necessary to fully validate the approach’s efficacy and generalizability. Finally, combining MOMBO with other techniques, such as model-based exploration strategies or advanced value function approximation methods, may lead to significant further performance gains. Exploring these directions could solidify MOMBO’s place as a state-of-the-art offline reinforcement learning algorithm.
More visual insights#
More on figures

🔼 This figure compares the performance of moment matching and Monte Carlo sampling in estimating the value of the next state for various tasks within the D4RL dataset. It visually demonstrates the advantage of moment matching in providing sharper estimates with significantly fewer samples compared to Monte Carlo methods, which exhibit high variance even with a large number of samples.
read the caption
Figure 3: Moment Matching versus Monte Carlo Sampling. A comparison of moment matching and Monte Carlo sampling methods for estimating the next value for all tasks in the D4RL dataset.
🔼 The figure compares the performance of moment matching and Monte Carlo sampling in estimating the action-value of the next state. Moment matching achieves sharp estimates with only two forward passes, while Monte Carlo sampling requires 10,000 samples to achieve similar accuracy, highlighting the efficiency gain of the proposed method.
read the caption
Figure 1: Moment Matching versus Monte Carlo Sampling. Moment matching offers sharp estimates of the action-value of the next state at the cost of only two forward passes through a critic network. A similar sharpness cannot be reached even with 10000 Monte Carlo samples, which is 5000 times more costly. See Appendix C.1.1 for details.

🔼 This figure compares the performance of moment matching and Monte Carlo sampling in estimating the Q-value of the next state. It shows the distributions of Q-values obtained using different numbers of Monte Carlo samples (2, 10, 100, 1000, 10000) compared to the distribution obtained using moment matching. The results illustrate the higher variance and slower convergence of Monte Carlo sampling compared to the moment-matching approach, which delivers sharper estimates with significantly fewer samples.
read the caption
Figure 3: Moment Matching versus Monte Carlo Sampling. A comparison of moment matching and Monte Carlo sampling methods for estimating the next value for all tasks in the D4RL dataset.

🔼 This figure compares the performance of moment matching and Monte Carlo sampling in estimating the value of the next state for various tasks within the D4RL dataset. It visualizes the distribution of action-value estimations obtained using different numbers of Monte Carlo samples (2, 10, 100, 1000, and 10000) and the moment matching approach. Each subfigure shows results for a specific environment and dataset combination from D4RL, plotting the probability density functions for both methods. The moment matching method consistently shows much sharper distributions, even with significantly fewer samples, indicating more precise and stable estimates compared to the Monte Carlo sampling-based approach.
read the caption
Figure 3: Moment Matching versus Monte Carlo Sampling. A comparison of moment matching and Monte Carlo sampling methods for estimating the next value for all tasks in the D4RL dataset.
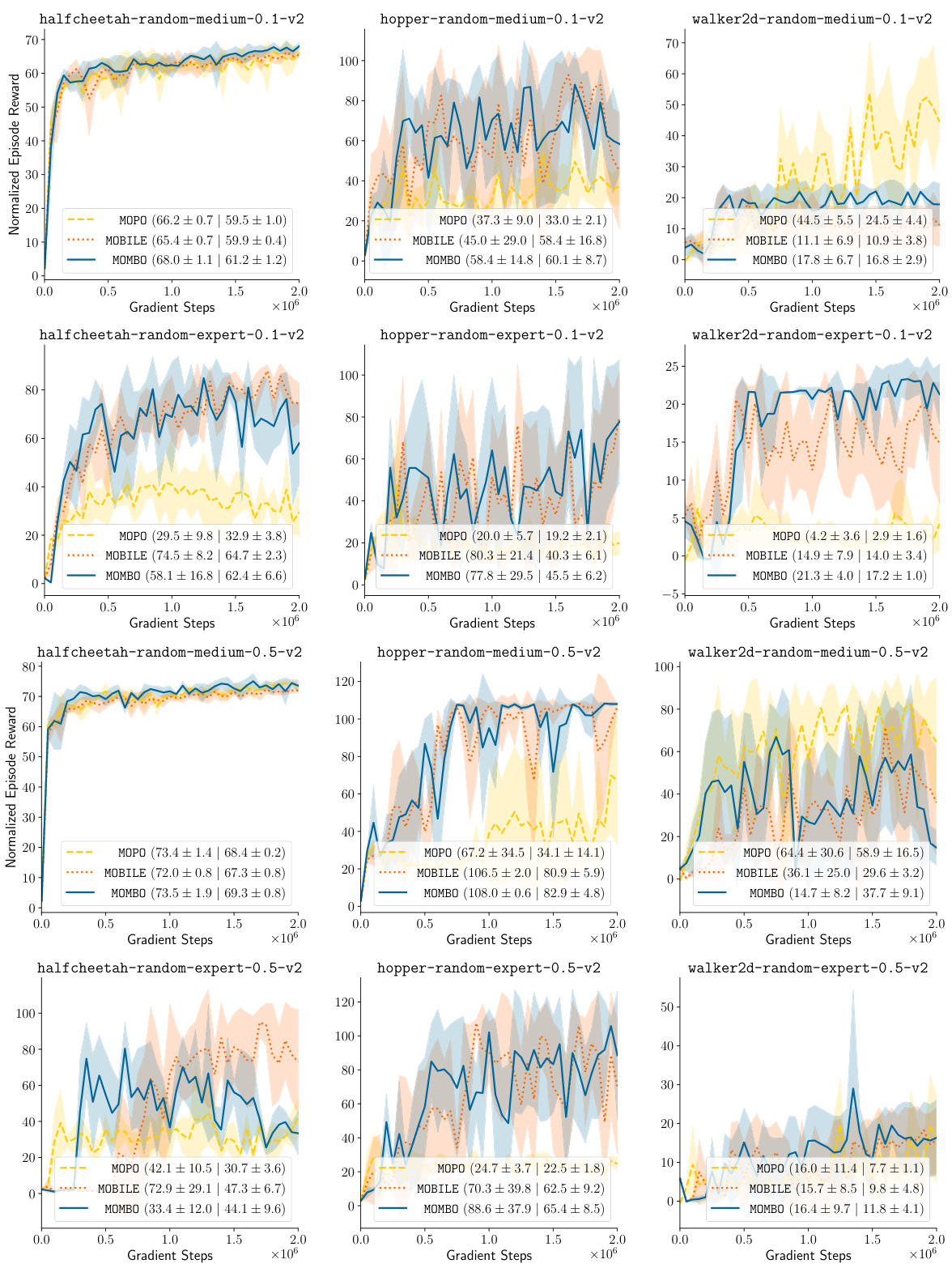
🔼 This figure compares the performance of moment matching and Monte Carlo sampling in estimating the value of the next state for various tasks within the D4RL dataset. It visually demonstrates the superior sharpness and reduced variance offered by the moment matching approach, especially when compared to Monte Carlo sampling, even with a substantially higher number of samples.
read the caption
Figure 3: Moment Matching versus Monte Carlo Sampling. A comparison of moment matching and Monte Carlo sampling methods for estimating the next value for all tasks in the D4RL dataset.
More on tables

🔼 This table presents the performance comparison of three offline reinforcement learning algorithms (MOPO, MOBILE, and MOMBO) across various tasks from the D4RL dataset. The results are evaluated using two metrics: Normalized Reward (the total episode reward normalized by the performance of random and expert policies) and Area Under the Learning Curve (AULC, which measures learning efficiency). The table shows the mean and standard deviation of these metrics across four repetitions of each experiment. Higher scores indicate better performance. The table also provides average scores and ranks to summarize the overall performance of the algorithms.
read the caption
Table 1: Performance evaluation on the D4RL dataset. Normalized reward at 3M gradient steps and Area Under the Learning Curve (AULC) (mean±std) scores are averaged across four repetitions for the MuJoCo domain of the D4RL offline reinforcement learning dataset. The highest means are highlighted in bold and are underlined if they fall within one standard deviation of the best score. The average normalized score is the average across all tasks. The average ranking is based on the rank of the mean.

🔼 This table presents the performance comparison of three offline reinforcement learning algorithms (MOPO, MOBILE, and MOMBO) on the D4RL dataset. The algorithms are evaluated across 12 tasks using two metrics: Normalized Reward (the total episode reward normalized by random and expert policy performance) and Area Under the Learning Curve (AULC, measuring the average reward over the course of training). The table shows mean and standard deviation scores averaged across four runs for each task and overall. High scores are better and bold/underlined scores are within one standard deviation of the best.
read the caption
Table 1: Performance evaluation on the D4RL dataset. Normalized reward at 3M gradient steps and Area Under the Learning Curve (AULC) (mean±std) scores are averaged across four repetitions for the MuJoCo domain of the D4RL offline reinforcement learning dataset. The highest means are highlighted in bold and are underlined if they fall within one standard deviation of the best score. The average normalized score is the average across all tasks. The average ranking is based on the rank of the mean.

🔼 This table presents the results of the performance evaluation on the D4RL dataset for three MuJoCo environments (halfcheetah, hopper, walker2d) and four levels of expertise (random, medium, medium-replay, and medium-expert). It shows the normalized reward (higher is better) and the area under the learning curve (AULC) (higher is better) for three algorithms: MOPO, MOBILE, and MOMBO. The average performance across all tasks, and the average ranking based on mean performance are also included.
read the caption
Table 1: Performance evaluation on the D4RL dataset. Normalized reward at 3M gradient steps and Area Under the Learning Curve (AULC) (mean±std) scores are averaged across four repetitions for the MuJoCo domain of the D4RL offline reinforcement learning dataset. The highest means are highlighted in bold and are underlined if they fall within one standard deviation of the best score. The average normalized score is the average across all tasks. The average ranking is based on the rank of the mean.

🔼 This table presents the performance comparison of three offline reinforcement learning algorithms (MOPO, MOBILE, and MOMBO) across various D4RL benchmark tasks. The evaluation metrics are the normalized reward (averaged over 3 million gradient steps and four repetitions) and the Area Under the Learning Curve (AULC). Higher values indicate better performance. The table also provides the average normalized reward and average ranking of the algorithms across all tasks.
read the caption
Table 1: Performance evaluation on the D4RL dataset. Normalized reward at 3M gradient steps and Area Under the Learning Curve (AULC) (mean±std) scores are averaged across four repetitions for the MuJoCo domain of the D4RL offline reinforcement learning dataset. The highest means are highlighted in bold and are underlined if they fall within one standard deviation of the best score. The average normalized score is the average across all tasks. The average ranking is based on the rank of the mean.
Full paper#