Zero-Shot Transfer of Neural ODEs

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it introduces a novel method for enabling zero-shot transfer in autonomous systems. This is a significant advance in the field of AI, as it allows autonomous systems to adapt quickly to new and unseen environments without the need for extensive retraining. The method is particularly relevant to applications where real-time adaptation is critical, such as robotics and autonomous driving. The approach opens up new avenues for research on adaptable control algorithms and efficient online learning techniques.

Visual Insights

#

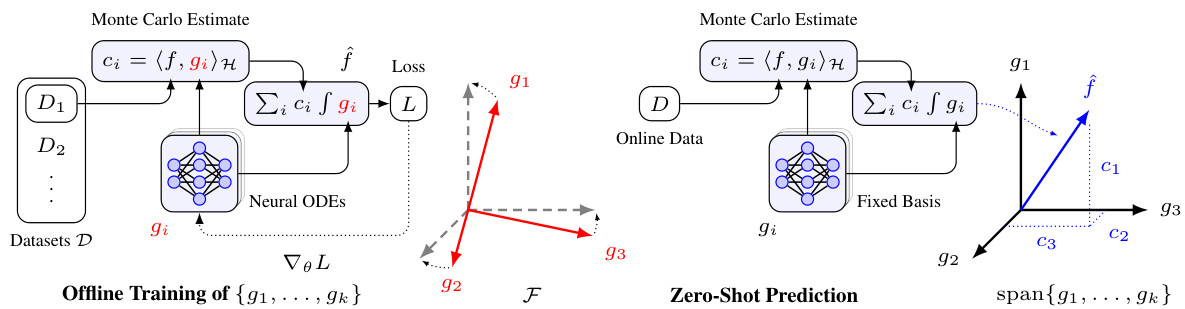
This figure illustrates the two phases of the proposed approach: offline training and zero-shot prediction. In the training phase, a set of datasets D is used to train a set of basis functions (g1,…,gk) which span the function space F. These basis functions are parameterized by neural ODEs. In the zero-shot prediction phase, online data is used to identify the coefficients for a new function f, which is then approximated as a linear combination of the pre-trained basis functions. This process does not require retraining.

In-depth insights

#

Neural ODE Basis

#

The concept of “Neural ODE Basis” proposes a novel approach to modeling dynamical systems. It leverages the power of neural ordinary differential equations (NODEs) to learn a set of basis functions that span the space of possible system dynamics. Instead of learning a single function, this method efficiently represents a space of functions, enabling zero-shot transfer to unseen scenarios. The basis functions, which are neural ODEs themselves, are trained offline on a diverse set of datasets representing various system behaviors. This offline training allows for the efficient identification of dynamics at runtime using minimal data. Online adaptation is then achieved via a rapid inner product calculation with no gradient updates needed, making it suitable for real-time applications. The key insight is that by learning the structure of the space of differential equations, the approach implicitly learns how dynamics change under environmental variations, dramatically improving adaptability.

Zero-Shot Transfer

#

Zero-shot transfer, a crucial concept in machine learning, is explored in this paper within the context of neural ordinary differential equations (NODEs). The core idea revolves around building a model that can generalize to unseen scenarios without requiring retraining. This is achieved by learning a space of dynamical systems, not individual systems. The paper proposes learning a set of basis functions (each a NODE) spanning this function space. New scenarios are then represented as linear combinations of these basis functions, allowing rapid adaptation at runtime. This innovative approach avoids expensive online training, making it suitable for autonomous systems that need to react quickly to changing environments. The key is in the efficient encoding of dynamics, not through retraining, but through inner product calculations which are computationally inexpensive. The efficacy is demonstrated through experiments involving MuJoCo robot environments and quadrotor control, showcasing improved accuracy and efficiency compared to traditional methods.

MuJoCo Experiments

#

The MuJoCo experiments section would likely detail the application of the proposed zero-shot transfer method for Neural ODEs to control robotic systems simulated within the MuJoCo physics engine. This would involve describing the specific robotic tasks used (e.g., HalfCheetah, Ant locomotion), how the learned models are used for prediction and control (possibly using Model Predictive Control or a similar technique), and a rigorous evaluation comparing the performance against baselines (like standard Neural ODEs or other zero-shot learning methods). Key aspects would include metrics such as prediction accuracy over various time horizons, control performance measured by task success rate or efficiency, and robustness to unseen dynamics or environmental variations. The discussion would analyze whether the learned models generalize effectively to different system configurations or parameters. A core element would be demonstrating zero-shot transfer capability; the model would be evaluated using only minimal online data without retraining. The results should demonstrate the superiority of the proposed approach in terms of adaptability and prediction/control accuracy. Finally, it would be essential to discuss how the results on the MuJoCo simulations translate to or inform the development of real-world robotic control systems.

Online Adaptation

#

The concept of ‘Online Adaptation’ in the context of this research paper centers on the ability of a model to quickly adjust to new, unseen data without requiring retraining. This is crucial for autonomous systems operating in dynamic environments where conditions change unpredictably. The core idea revolves around learning a space of functions (representing the system’s possible behaviors) beforehand, using offline data. This pre-training phase builds a set of basis functions, parameterized by neural ODEs, that span this function space. During online operation, the model efficiently identifies the relevant dynamics from the pre-trained space using inner product calculations on minimal online data. This avoids expensive online gradient calculations and retraining, allowing for rapid adaptation to new scenarios. The methodology represents a significant advance toward achieving zero-shot transfer in autonomous systems, providing efficient and robust adaptation in real-time.

Future Work

#

The paper’s “Future Work” section would benefit from exploring several key areas. Extending the theoretical framework to stochastic differential equations and Hilbert spaces of probability measures would significantly enhance its applicability to real-world scenarios with inherent uncertainty. Addressing safety during the training phase is crucial for deploying such models in safety-critical applications. This could involve incorporating methods to bound prediction errors and enhance robustness against adversarial inputs or noisy data. Investigating the sim-to-real gap requires attention. While the model’s ability to generalize is promising, it’s essential to assess how well it performs with real-world data after being trained with simulated data. This might include strategies to reduce the reliance on simulation and use a more hybrid approach. Finally, empirical testing on even more complex tasks is needed to fully demonstrate the capabilities of this approach, building upon the work with quadrotors and MuJoCo environments. Investigating the scalability and efficiency of the proposed methodology for diverse scenarios would be a worthy pursuit.

More visual insights

#

More on figures

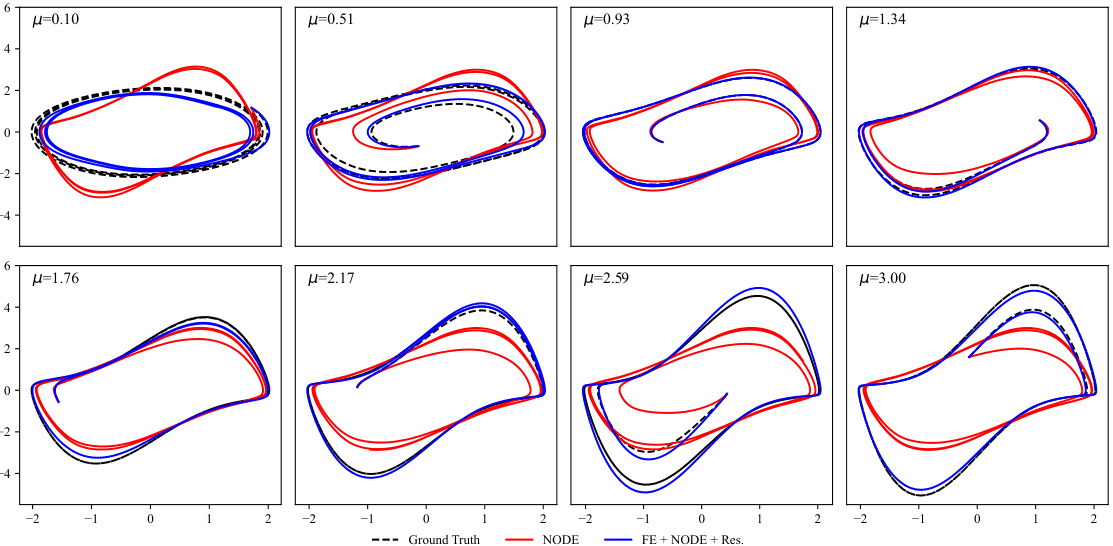
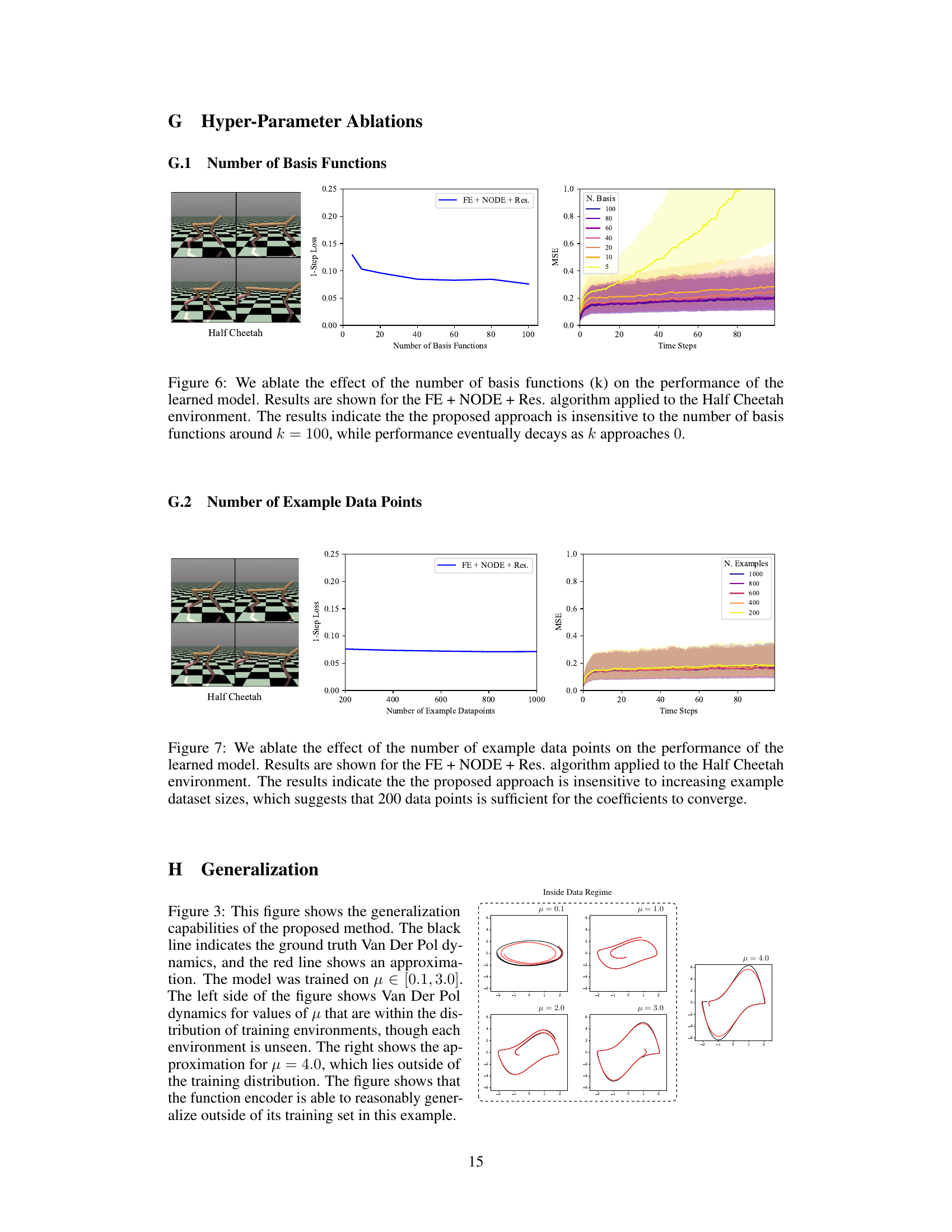
This figure compares the performance of different methods for approximating the dynamics of Van der Pol oscillators with varying parameters (μ). The top row shows the results for different values of μ using a Neural ODE (NODE) method, demonstrating the NODE’s inability to generalize across different parameter settings. The bottom row displays results obtained using the proposed method (Function Encoder + Neural ODE + Residuals, or FE + NODE + Res), showcasing its ability to capture a broader space of dynamical systems. The dashed black lines represent the ground truth trajectories, highlighting the superior accuracy and generalization capability of the FE + NODE + Res method.

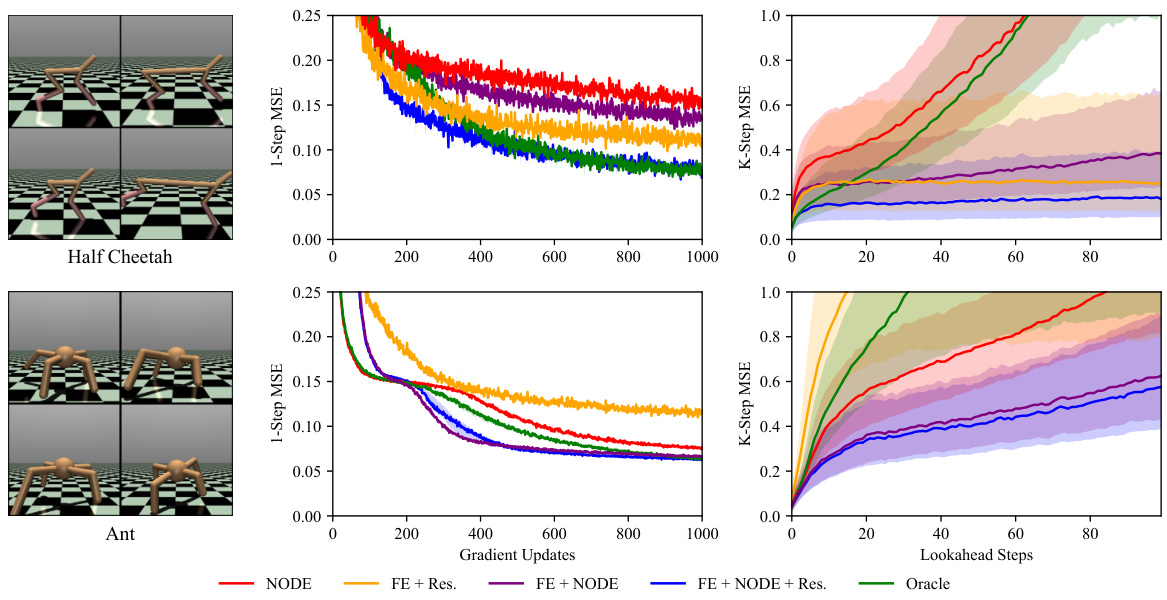
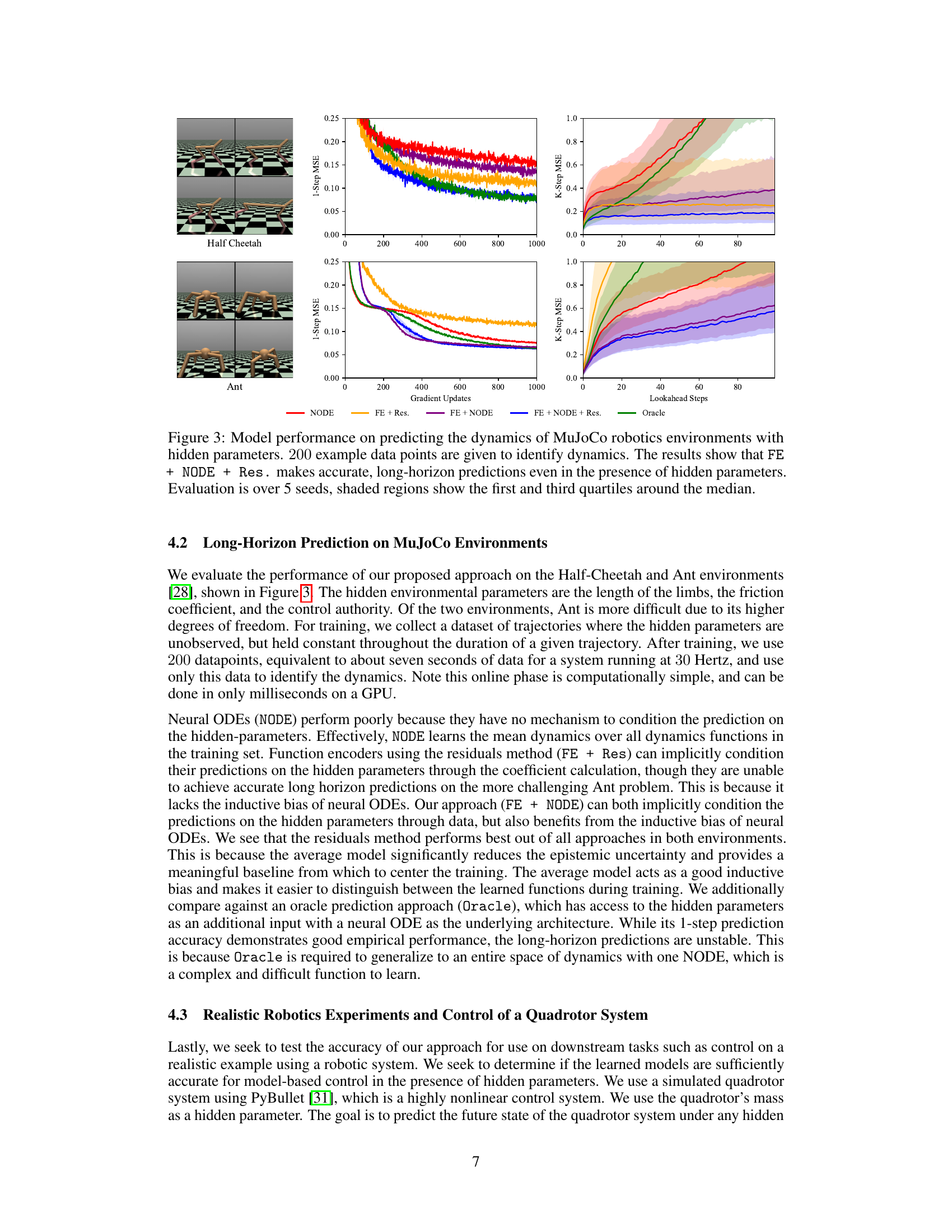
This figure compares the performance of different methods (NODE, FE + Res., FE + NODE, FE + NODE + Res., and Oracle) on predicting the dynamics of two MuJoCo robotics environments (Half Cheetah and Ant) with hidden parameters. The plots show 1-step and k-step Mean Squared Error (MSE) over gradient updates and lookahead steps. The FE + NODE + Res method demonstrates superior performance in long-horizon prediction accuracy, even with limited data and hidden parameters. The shaded regions represent the uncertainty around the median performance across multiple trials.

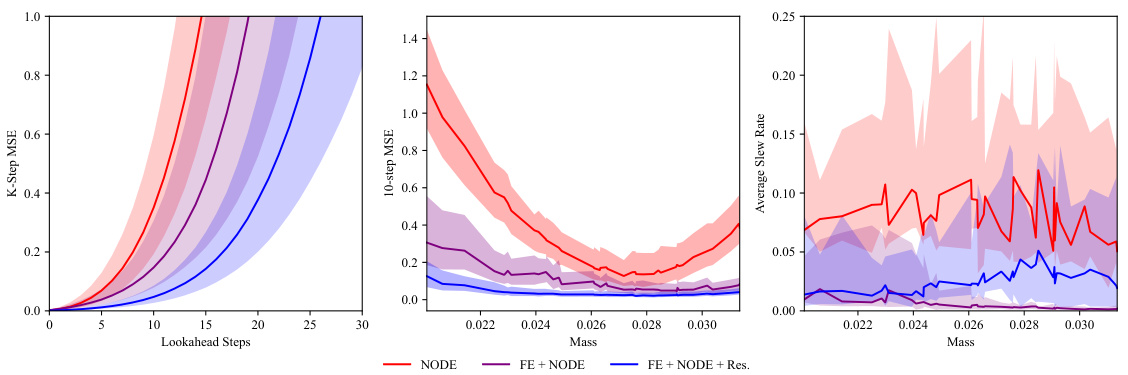
This figure presents a comparison of different model’s performance on predicting the dynamics of two MuJoCo environments (Half-Cheetah and Ant) with hidden parameters. The models being compared are NODE, FE+Res, FE+NODE, and FE+NODE+Res. The x-axis represents the number of gradient updates or lookahead steps, and the y-axis represents the 1-step or k-step Mean Squared Error (MSE). The shaded regions indicate the interquartile range (IQR) across 5 different trials, showcasing the model’s robustness and predictive accuracy. The figure demonstrates that the FE+NODE+Res model consistently outperforms other models, especially in terms of long-horizon prediction accuracy (k-step MSE).

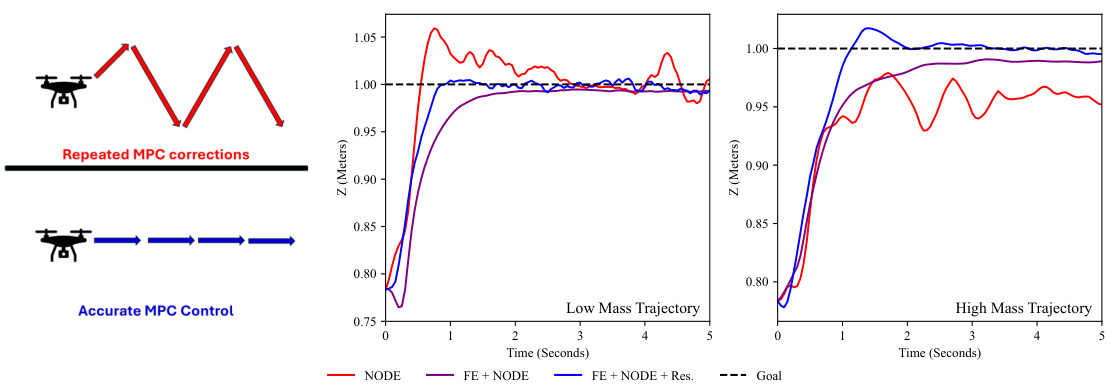
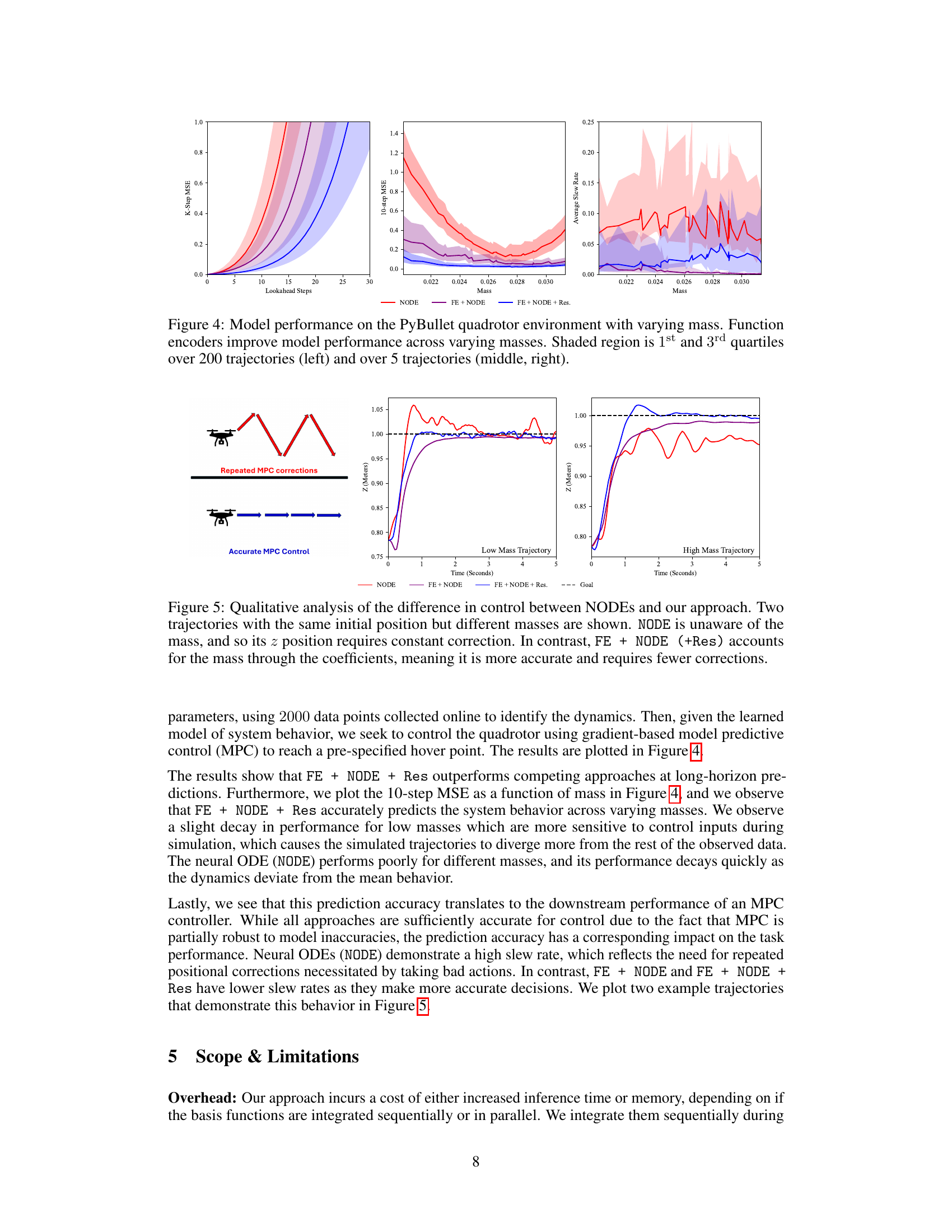
This figure compares the performance of Neural ODEs (NODE) and the proposed Function Encoder + Neural ODE (+Res) approach in controlling a quadrotor’s altitude (z-axis). Two trajectories are shown, one with a low mass and one with a high mass. The NODE approach, unaware of the mass, demonstrates significant oscillations and requires frequent corrections to maintain altitude. In contrast, the FE + NODE (+Res) approach accurately tracks the desired altitude in both scenarios, showing robustness against variations in system parameters.

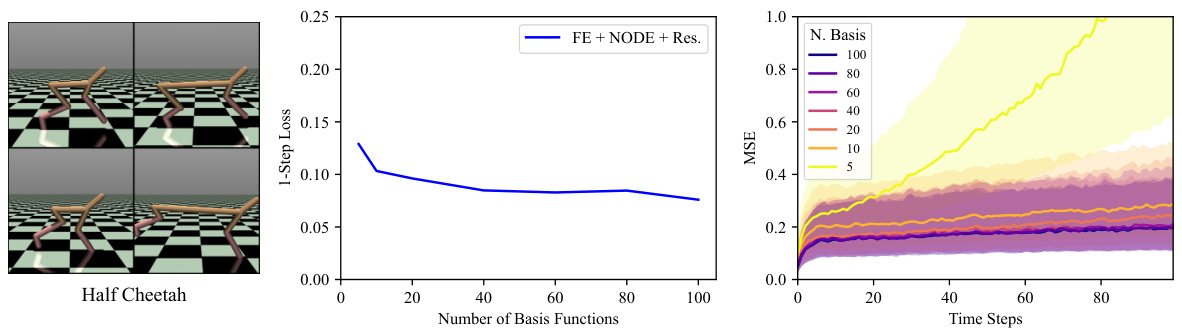
This figure shows the ablation study on the number of basis functions used in the FE + NODE + Res. model for the Half Cheetah environment. The left panel shows example frames from the Half Cheetah environment. The middle panel is a line plot showing that the 1-step loss decreases as the number of basis functions increases but plateaus around k=100. The right panel is a shaded area plot showing that the MSE over time steps is low when using approximately 100 basis functions but increases if too few or too many are used.

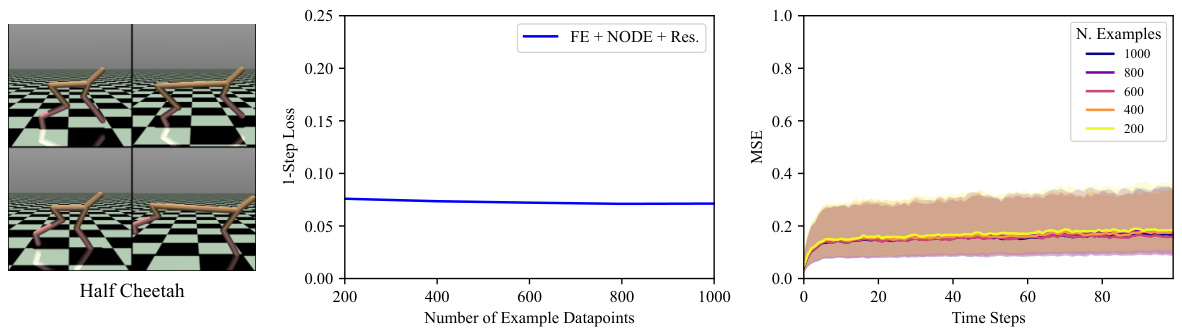
This figure shows the ablation study on the number of example data points used in the training phase of the proposed method, FE + NODE + Res, on the Half Cheetah environment. The plot demonstrates the model’s robustness to the amount of training data; even with just 200 data points, the model achieves good performance. Increasing the number of data points does not improve the performance significantly, indicating that 200 data points is sufficient to train the model effectively.

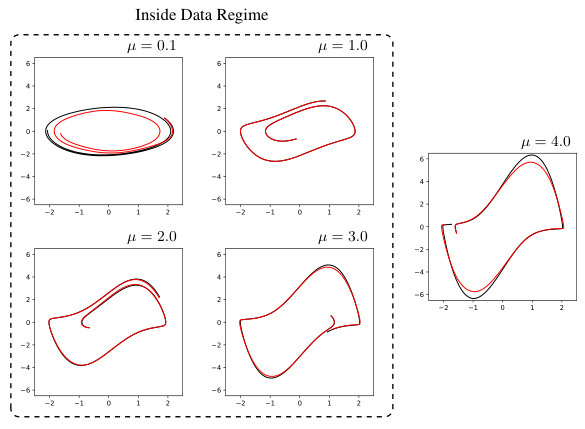
This figure compares the performance of Neural ODEs (NODE) and Function Encoders with Neural ODEs and Residuals (FE + NODE + Res) on approximating the dynamics of Van der Pol oscillators with varying parameters (μ). NODE struggles to generalize across different μ values, while FE + NODE + Res effectively learns a representation that captures the behavior across a wide range of μ values. The plot shows several trajectories for each method and different μ values, illustrating FE + NODE + Res’s superior ability to accurately model different dynamics without retraining.

Full paper

#