↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Approximate Nearest Neighbor Search (ANNS) is a computationally expensive task crucial for various applications. Existing state-of-the-art ANNS algorithms often build large proximity graphs, leading to many unnecessary computations during search. This paper addresses this limitation by proposing a novel framework.
The proposed framework, called Crossing Sparse Proximity Graphs (CSPG), divides the dataset into smaller partitions, creating a sparse proximity graph for each. An efficient two-staged search strategy, combining fast approaching and cross-partition expansion, is designed to traverse these graphs effectively. Theoretical analysis proves that CSPG reduces computations compared to traditional methods. Extensive experiments demonstrate significant speed improvements (1.5x to 2x) across various datasets and ANNS algorithms.
Key Takeaways#
Why does it matter?#
This paper is important because it significantly speeds up approximate nearest neighbor search (ANNS), a crucial task in many applications. The proposed CSPG framework offers a general solution that can be integrated with existing ANNS algorithms, improving their efficiency without sacrificing accuracy. This opens new avenues for research in optimizing ANNS for large-scale datasets and various applications.
Visual Insights#
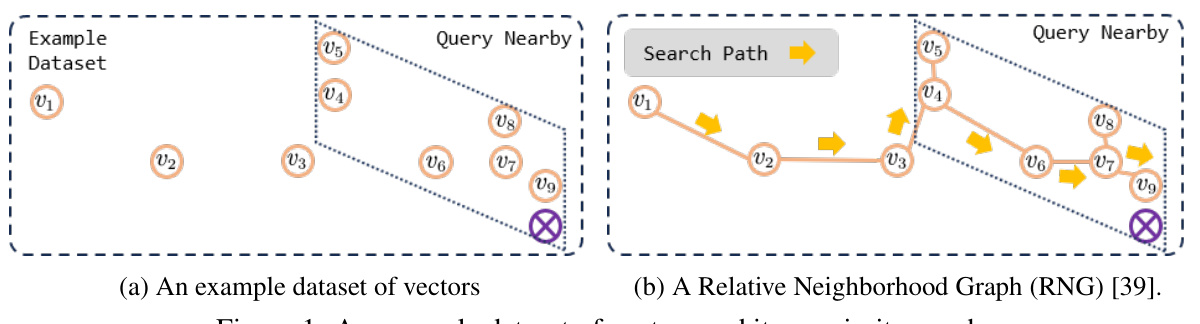
The figure shows an example dataset of vectors represented as nodes and their proximity graph which visualizes the relationships between the vectors. (a) shows the dataset in a 2D space, and (b) illustrates a Relative Neighborhood Graph (RNG) constructed from this data, demonstrating how vectors with closer proximity are connected by edges.

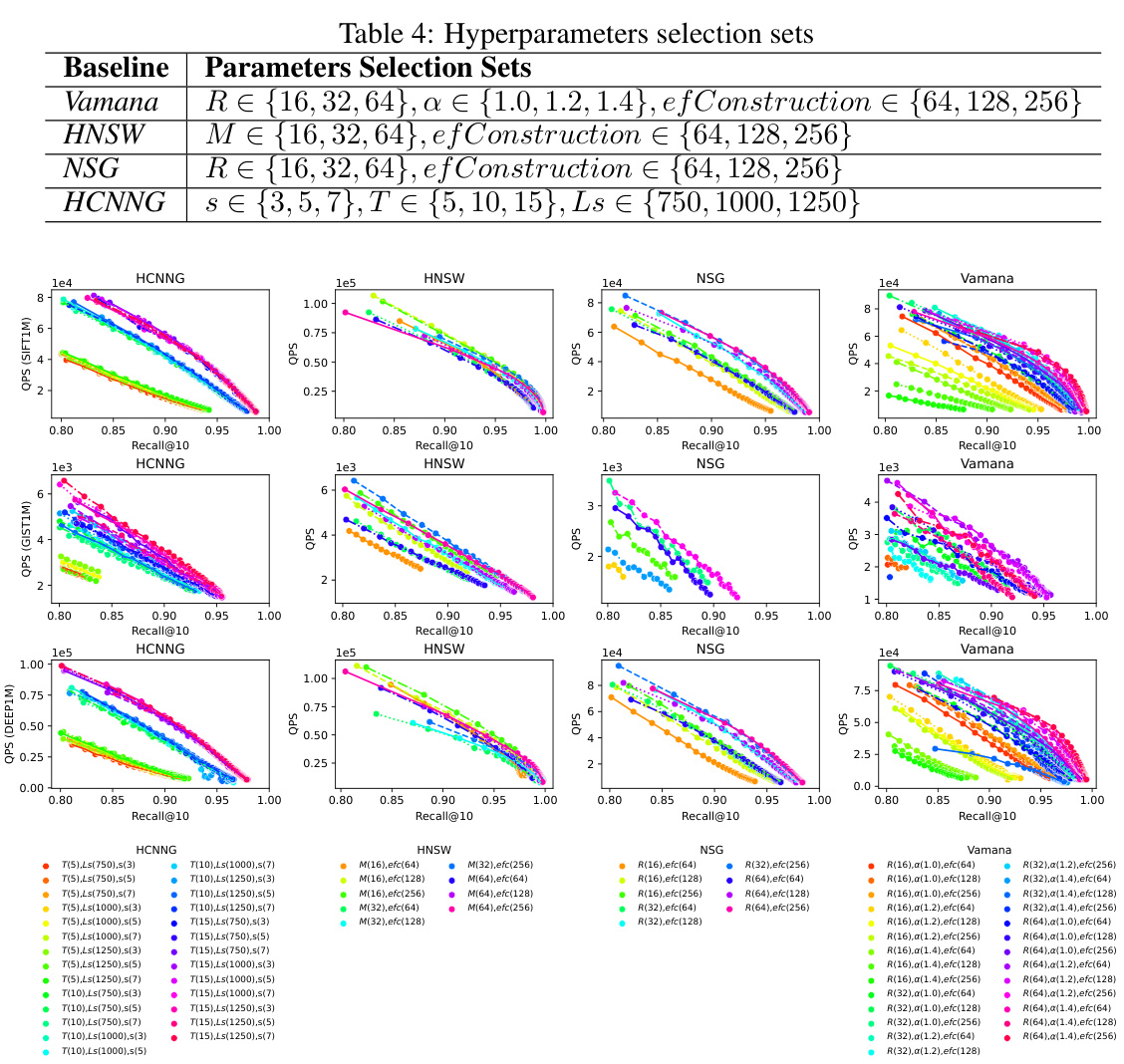
This table compares the index construction costs of four different graph-based approximate nearest neighbor search algorithms (HNSW, Vamana, HCNNG) and their corresponding CSPG versions across four datasets (SIFT1M, GIST1M, DEEP1M, SIFT10M). For each algorithm and dataset, it presents the data size (DS), index size (IS), and index construction time (IT). The table allows for a comparison of the overhead introduced by CSPG in terms of index size and construction time, relative to the original graph-based algorithms.
In-depth insights#
CSPG Framework#
The CSPG framework introduces a novel approach to approximate nearest neighbor search (ANNS) by employing random partitioning of the dataset. Instead of building one large proximity graph, CSPG constructs multiple smaller, sparser graphs for each partition. This significantly reduces the computational cost associated with traditional graph-based ANNS methods. Routing vectors act as bridges connecting these smaller graphs, enabling efficient search traversal across partitions. The two-staged search strategy, involving fast approaching within a single partition followed by cross-partition expansion, further optimizes the search process. Theoretically, CSPG is proven to reduce unnecessary explorations, aligning with experimental results showing 1.5x to 2x speedups. The framework’s adaptability is a key strength; it can integrate with various existing graph-based ANNS algorithms, enhancing their performance without compromising accuracy.
Two-Stage Search#
The proposed two-stage search strategy for the Crossing Sparse Proximity Graph (CSPG) framework is a key innovation for efficient approximate nearest neighbor search. The first stage employs a fast approaching method, focusing on a single, smaller proximity graph to quickly narrow down the search space. This is crucial for efficiency, as it avoids unnecessary computations in the initial phase. The second stage, cross-partition expansion, leverages routing vectors to seamlessly transition between partitions, extending the search to other graphs for more precise results. This dynamic transition across partitions is what differentiates CSPG from traditional single-graph approaches. By carefully managing candidate set sizes (ef1 and ef2) across the two stages, the algorithm balances speed and accuracy. The theoretical analysis supports the efficiency gains, showing that the expected search cost of CSPG is comparable to a much smaller graph. The two-stage design effectively combines the benefits of fast initial exploration and thorough, precise search, ultimately delivering improved query performance compared to existing graph-based methods.
Theoretical Analysis#
A theoretical analysis section in a research paper would typically delve into a formal mathematical justification of the proposed method’s efficacy. It would likely involve defining key parameters, establishing relevant assumptions about data distribution or model behavior, and then deriving theorems or propositions that demonstrate the method’s effectiveness under specific conditions. For instance, the authors might prove that their algorithm achieves a certain level of accuracy or speedup compared to existing approaches, perhaps showing a reduced computational complexity or a tighter error bound. The strength of the analysis hinges on the rigor of the mathematical proof and the relevance of the assumptions to real-world scenarios. A well-crafted theoretical analysis not only provides assurance about the proposed method’s performance but also offers deeper insights into its underlying mechanisms, providing a strong foundation for empirical validation.
Empirical Results#
An ‘Empirical Results’ section of a research paper would ideally present a thorough evaluation of the proposed method. Quantitative results showing improvements over existing approaches should be clearly presented, using appropriate metrics and statistical significance tests where necessary. The section should go beyond simply reporting numbers; it should provide insightful analysis and discussion of the results. This might include examining the impact of different parameters on performance, exploring the method’s behavior under various conditions, and comparing performance across different datasets. Visualizations such as graphs or tables should be used to effectively communicate the findings. Furthermore, a discussion of any unexpected or surprising results would demonstrate critical thinking, while potential limitations of the experimental setup should be acknowledged and discussed in order to enhance the paper’s credibility. Robustness analysis, showing the consistency of improvements across different datasets or parameter settings, is critical for building confidence in the proposed approach. Finally, a concise conclusion summarizing the key findings and their implications, possibly in relation to the research’s goals, is essential.
Future Directions#
Future research could explore several promising avenues. Improving the theoretical analysis of CSPG’s performance under more relaxed assumptions about data distribution is crucial. Currently, the theoretical guarantees rely on specific conditions; a more robust analysis accounting for real-world dataset complexities would significantly enhance the framework’s applicability. Extending CSPG to other distance metrics beyond Euclidean distance would broaden its utility across diverse applications. Incorporating techniques for handling dynamic datasets with frequent insertions and deletions would be important for online applications. Investigating the optimal number of partitions and the tradeoffs between computational speed and accuracy in relation to data characteristics would help users choose the optimal parameters for their datasets. Finally, comparing CSPG with state-of-the-art ANNS techniques, especially those based on transformer models, in a comprehensive benchmark study could reveal the full potential and limitations of this promising framework.
More visual insights#
More on figures

This figure shows an example of a CSPG index. It illustrates how the dataset is randomly partitioned into subsets (P1 and P2 in this case), and each subset has its own sparse proximity graph (G1 and G2, built using relative neighborhood graphs). The key point is that the partitions share common vectors (routing vectors, highlighted in red), which allow the greedy search algorithm to traverse between different partitions during the search process, improving efficiency. The green graph represents G1 and the blue graph represents G2.
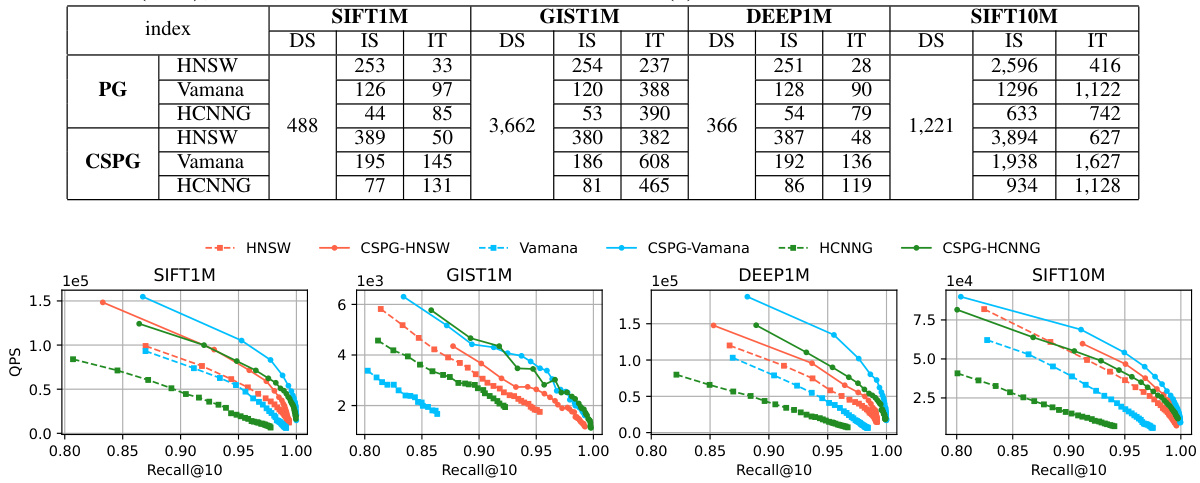
This figure shows the query performance (Queries Per Second or QPS) against the recall@10 for different datasets (SIFT1M, GIST1M, DEEP1M, SIFT10M) and various approximate nearest neighbor search (ANNS) algorithms. The algorithms include HNSW, Vamana, and HCNNG, both in their original forms and enhanced with the proposed CSPG framework. The plot illustrates the speedup achieved by integrating CSPG into existing ANNS algorithms. It shows that CSPG consistently improves the QPS across all datasets and algorithms at a fixed recall, suggesting a significant performance enhancement.
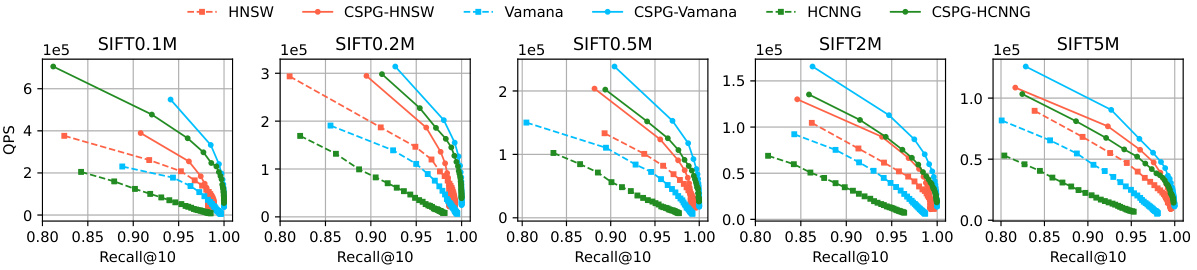
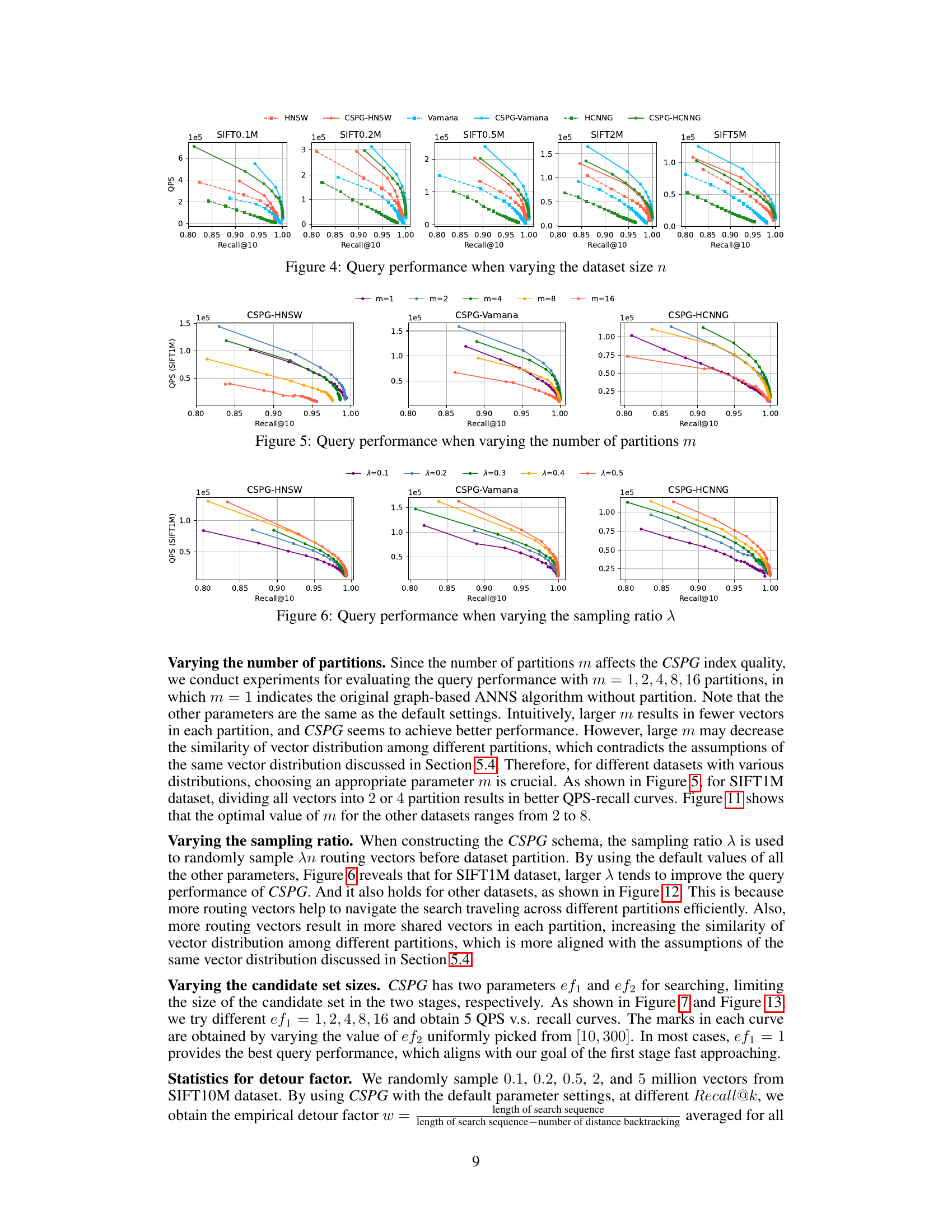
This figure displays the Query Performance per Second (QPS) versus Recall@10 for different dataset sizes (n). The datasets are variations of the SIFT dataset, ranging from 0.1 million to 5 million vectors. Each line represents the performance of a specific algorithm, with solid lines indicating the CSPG-enhanced versions and dashed lines representing the original algorithms (HNSW, Vamana, and HCNNG). The results show that CSPG consistently improves performance across all dataset sizes and algorithms, though the improvement is less dramatic as the dataset size grows.
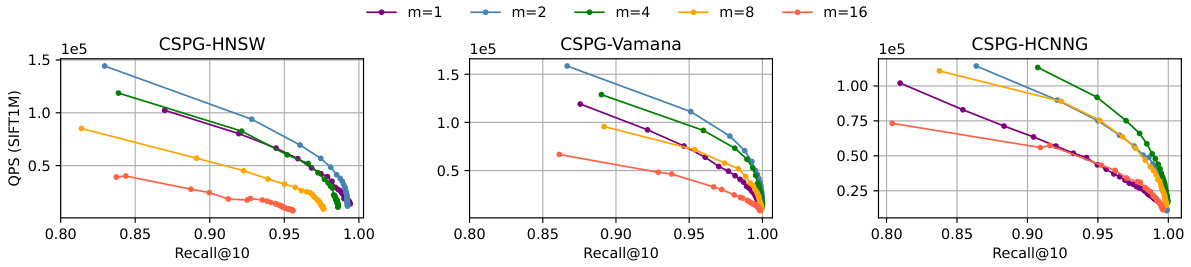
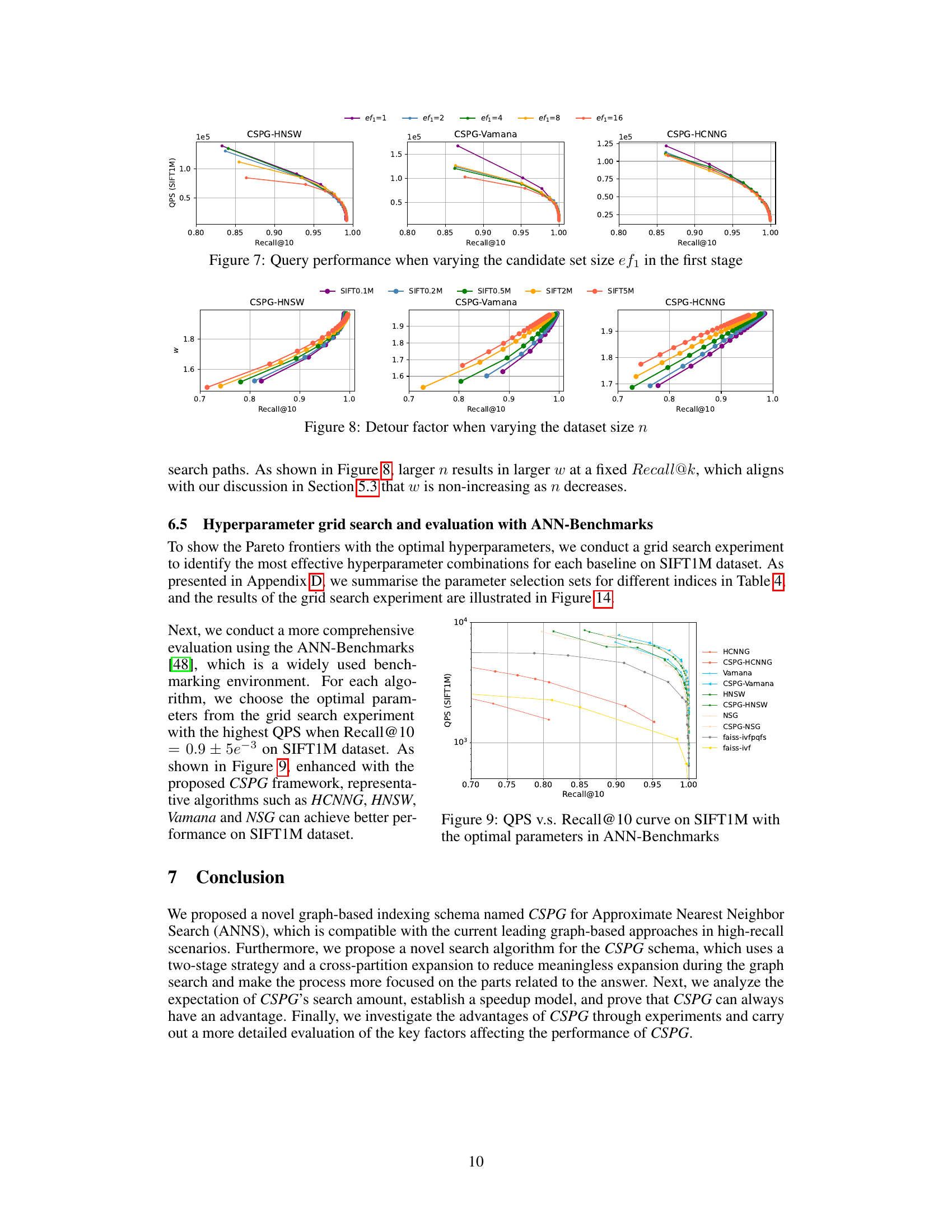
This figure shows the impact of varying the number of partitions (m) on the query performance (QPS) of the CSPG method. It presents QPS vs. Recall@10 curves for three different graph-based ANNS algorithms (HNSW, Vamana, and HCNNG) integrated with CSPG. Each curve represents a different number of partitions, allowing for comparison of how the choice of m affects the speed and accuracy of the approximate nearest neighbor search. The results indicate that a moderate number of partitions usually yields optimal performance, with extremes (too few or too many) degrading performance.

This figure displays the impact of varying the sampling ratio (λ) on the query performance of the CSPG method across different recall levels. The sampling ratio determines the proportion of vectors randomly selected as routing vectors before partitioning the dataset. The figure shows that for each of the three graph-based ANNS algorithms (HNSW, Vamana, and HCNNG), the performance generally increases with a higher sampling ratio. This suggests that having a greater number of routing vectors improves the effectiveness of navigating across the different partitions during the search.
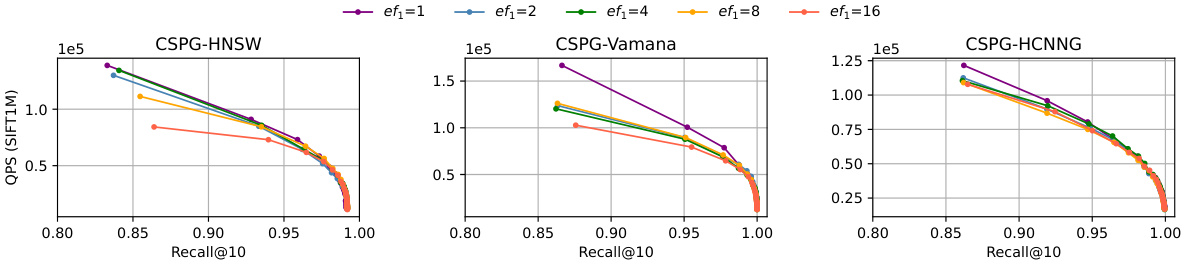
This figure shows how the query performance (QPS) of the CSPG method varies with different candidate set sizes (ef1) in the first stage of the two-stage search process. It compares three different graph-based ANNS algorithms (HNSW, Vamana, and HCNNG) enhanced with CSPG. The x-axis represents the recall@10, and the y-axis represents the QPS. Each line represents a different ef1 value, illustrating the trade-off between speed and accuracy. A smaller ef1 leads to faster query times but potentially lower accuracy, while a larger ef1 results in higher accuracy but slower queries.

This figure displays the detour factor (w) against Recall@10 for different dataset sizes (n) using three different graph-based ANNS algorithms integrated with CSPG. The detour factor represents the extent to which the search paths deviate from monotonicity. The figure illustrates how the detour factor changes with varying dataset sizes, providing insight into the impact of data size on search efficiency and monotonicity.
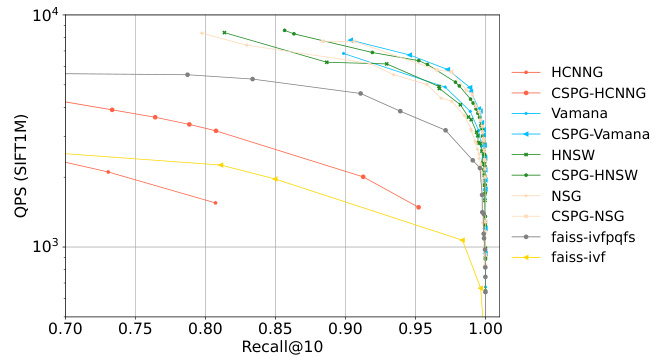
This figure shows the query performance (Queries Per Second or QPS) against the recall@10 for different approximate nearest neighbor search (ANNS) algorithms. It compares the performance of several traditional ANNS algorithms (HNSW, Vamana, HCNNG, NSG, and two faiss implementations) against their enhanced versions that incorporate the Crossing Sparse Proximity Graphs (CSPG) framework proposed in the paper. The x-axis represents the recall@10 (the fraction of the top 10 nearest neighbors correctly retrieved), and the y-axis represents the QPS. The plot demonstrates that the CSPG-enhanced algorithms consistently outperform their base counterparts across various recall levels, showcasing the effectiveness of the CSPG framework in improving query efficiency while maintaining a high recall rate.
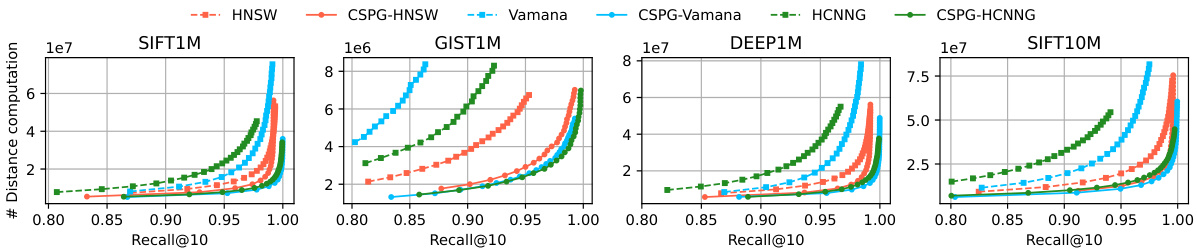
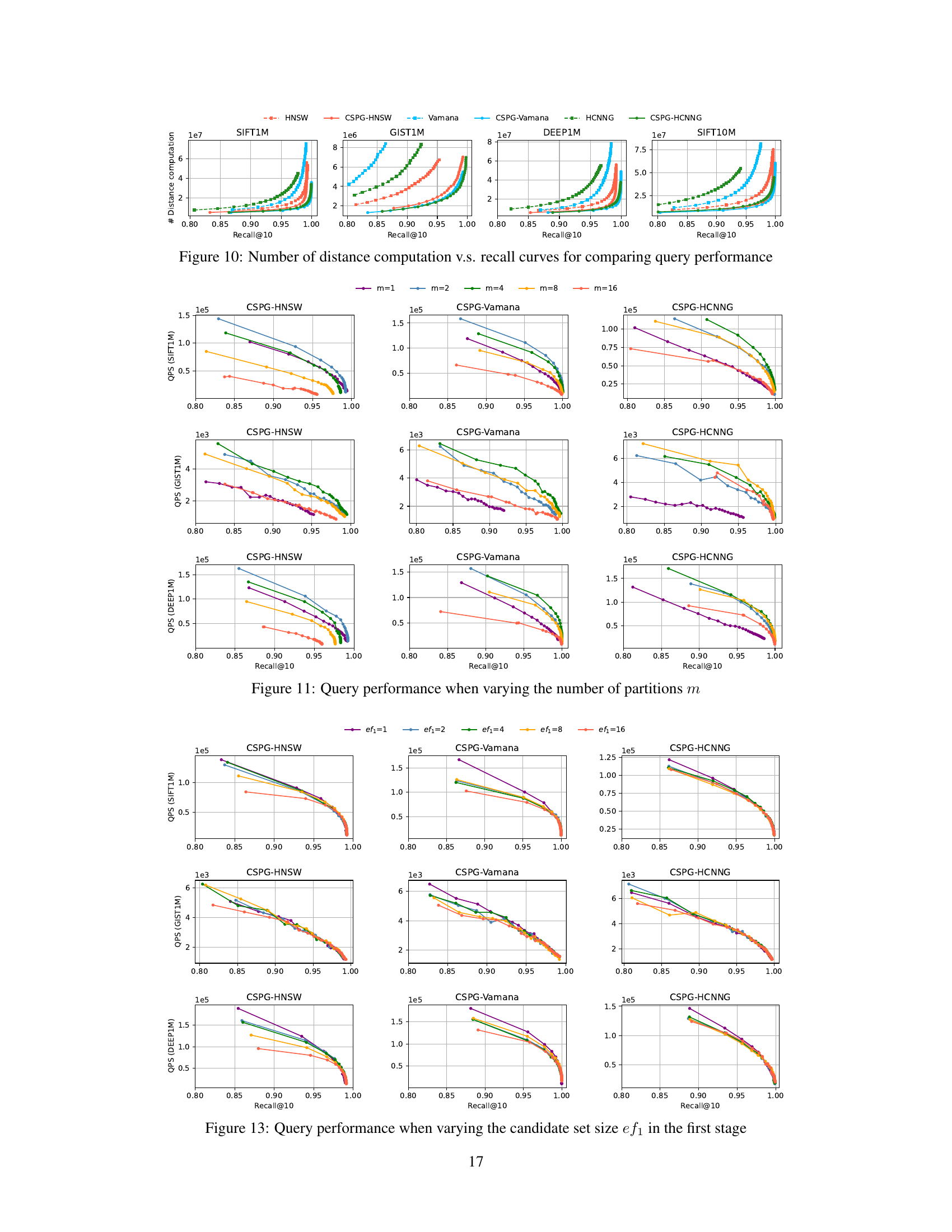
This figure compares the number of distance computations required by the original graph-based ANNS algorithms (HNSW, Vamana, and HCNNG) and their CSPG enhanced versions across four benchmark datasets (SIFT1M, GIST1M, DEEP1M, and SIFT10M) at varying recall@10 values. It illustrates the reduction in distance computations achieved by incorporating CSPG into each algorithm. The x-axis represents the recall@10, and the y-axis represents the number of distance computations. Each line represents a different algorithm, with solid lines representing the original algorithms and dashed lines representing their CSPG counterparts. The figure visually demonstrates the efficiency gains obtained by using CSPG.
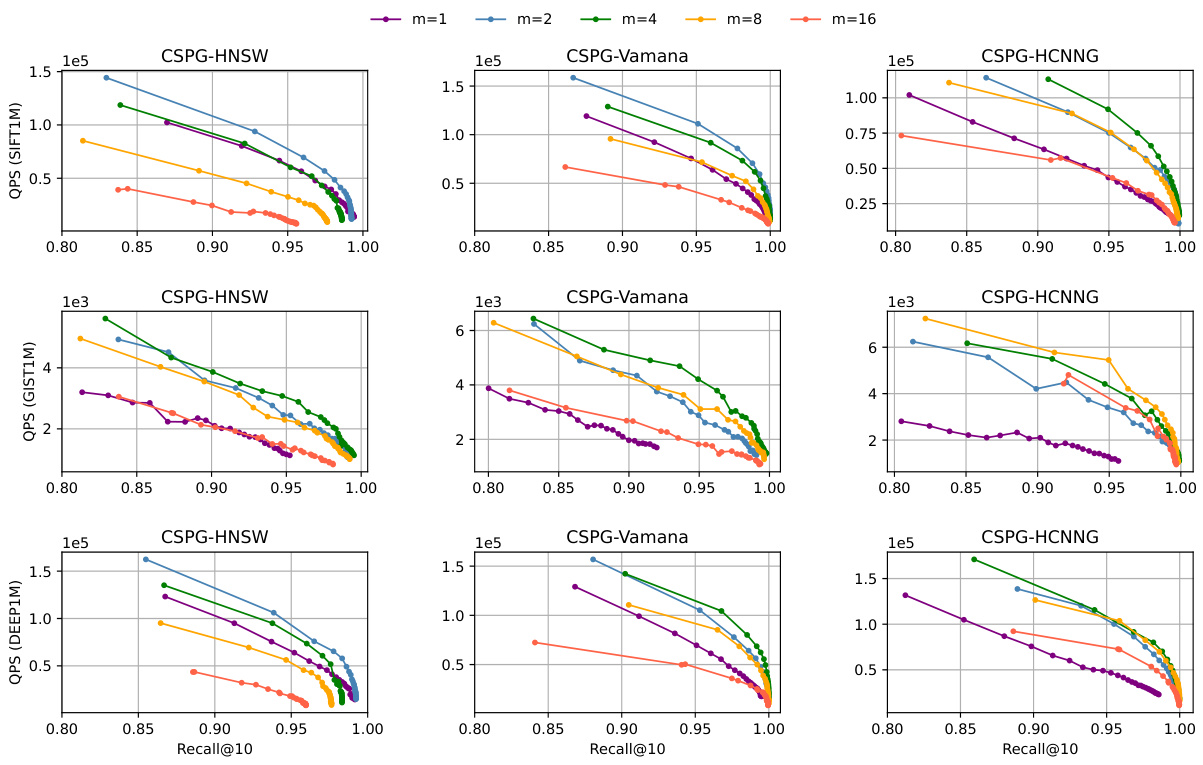
This figure shows the impact of varying the number of partitions (m) on the query performance of the CSPG method. It displays QPS (Queries Per Second) versus Recall@10 for different values of m (1, 2, 4, 8, 16). The results are shown for three datasets (SIFT1M, GIST1M, and DEEP1M) and three graph-based ANNS algorithms integrated with CSPG (HNSW, Vamana, and HCNNG). The figure illustrates how the choice of m affects the balance between speed and accuracy for each algorithm and dataset.
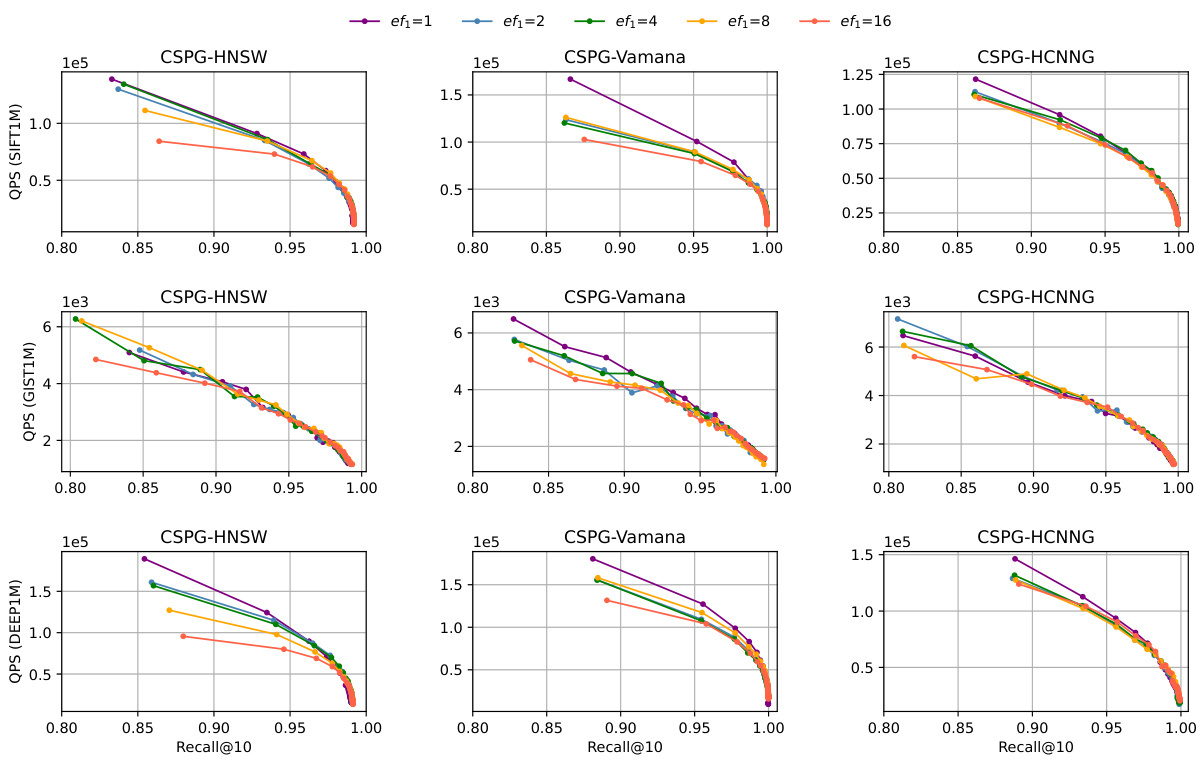
This figure shows the impact of varying the candidate set size (ef1) in the first stage of the CSPG search algorithm on the query performance. It presents QPS (Queries Per Second) versus Recall@10 curves for three different graph-based ANNS algorithms (HNSW, Vamana, HCNNG) enhanced by CSPG. Each curve within a subplot represents a different ef1 value, demonstrating how this parameter affects the trade-off between speed and accuracy across various datasets (SIFT1M, GIST1M, DEEP1M). The results illustrate how the choice of ef1 influences the algorithm’s efficiency and effectiveness in quickly approaching the query vector.
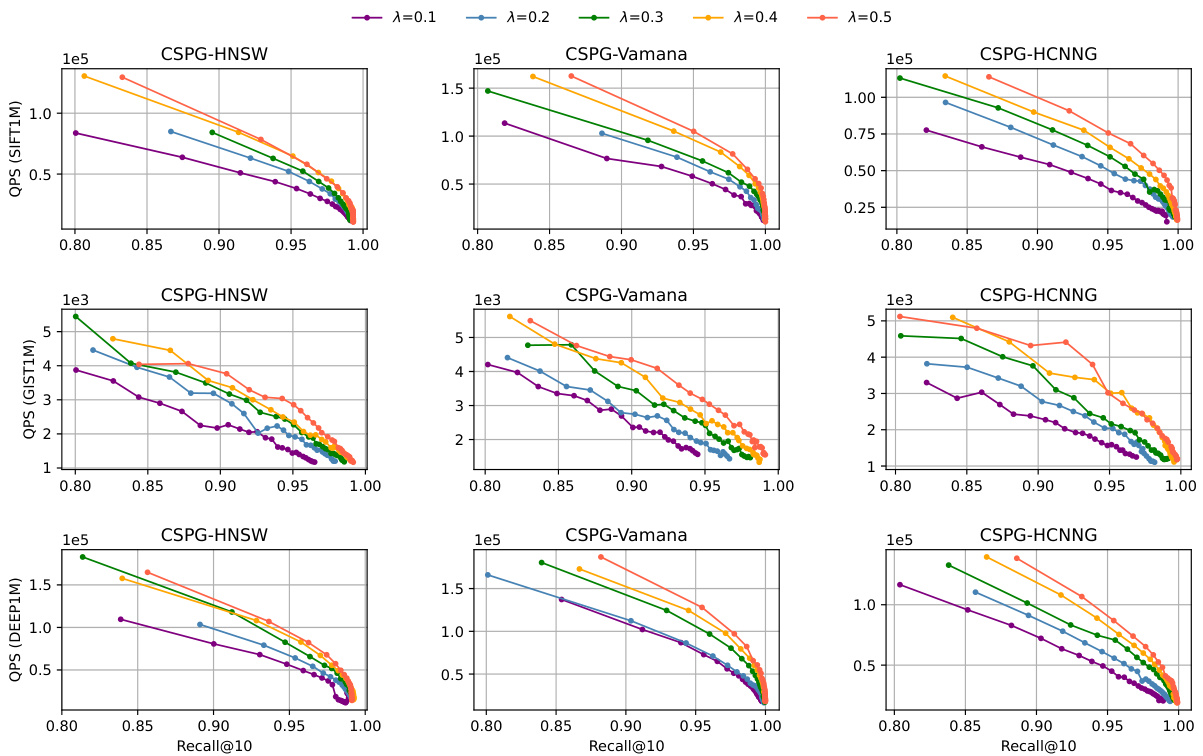
This figure shows the impact of varying the sampling ratio λ on the query performance of CSPG with different graph-based ANNS algorithms (HNSW, Vamana, and HCNNG) across various datasets (SIFT1M, GIST1M, and DEEP1M). The x-axis represents Recall@10, and the y-axis represents QPS (Queries Per Second). Each line represents a different value of λ, ranging from 0.1 to 0.5. The results demonstrate that changes in λ affect the trade-off between recall and query speed. Higher values of λ generally lead to better recall but lower QPS, suggesting a balance needs to be found between the number of routing vectors and the sparsity of individual graphs.
This figure compares the query performance of the CSPG method with the baseline methods (HNSW, Vamana, and HCNNG) across four benchmark datasets (SIFT1M, GIST1M, DEEP1M, and SIFT10M). It showcases the QPS (Queries Per Second) achieved at different recall levels (@10). The results demonstrate that CSPG consistently outperforms the baseline algorithms in terms of query speed for various recall levels, highlighting the efficiency gains achieved by the proposed approach.
More on tables
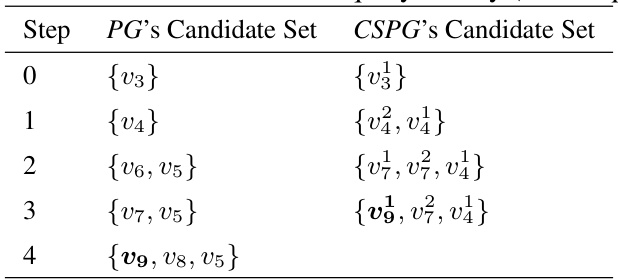
This table compares the candidate sets generated during a search in the vicinity of a query point for both a traditional proximity graph (PG) and the proposed Crossing Sparse Proximity Graph (CSPG) method. Each row represents a step in the search. The PG column shows the candidate set considered at each step when searching the entire graph. The CSPG column shows the candidate set for the same search steps but utilizing the CSPG approach. The superscripts in the CSPG column indicate the partition number from which each candidate vector originates. This illustrates the smaller candidate sets generated by CSPG and how vectors from different partitions can become candidates in the second stage, demonstrating the cross-partition expansion strategy.

This table compares the index construction cost of four different graph-based Approximate Nearest Neighbor Search (ANNS) algorithms: HNSW, Vamana, HCNNG, and their corresponding versions integrated with the proposed CSPG framework (CSPG-HNSW, CSPG-Vamana, CSPG-HCNNG). For each algorithm and dataset, it presents the data size (DS) in MB, the index size (IS) in MB, and the index construction time (IT) in seconds. The table provides insights into the space and time efficiency trade-offs of various ANNS methods, particularly how the CSPG framework affects the construction cost.
Full paper#