↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Transformers, the backbone of many AI models, rely on self-attention mechanisms to process information. However, the theoretical understanding of their complex dynamics, particularly under causal masking (where tokens only attend to previous tokens), remains limited. Existing studies often rely on simplifying assumptions that don’t fully capture real-world scenarios.
This paper tackles this challenge by analyzing causal self-attention as an interacting particle system on a sphere. The authors prove that the system asymptotically converges to a single cluster for arbitrary key-query matrices and an identity value matrix. They also establish a connection to the Rényi parking problem, a concept from combinatorial geometry, to explain the formation of meta-stable states. These are clusters that persist for extended periods even though they are not the ultimate equilibrium state, a phenomenon often observed in simulations but not well understood theoretically.
Key Takeaways#
Why does it matter?#
This paper is crucial because it offers a novel mathematical framework for analyzing the behavior of transformers, a cornerstone of modern AI. Understanding transformer dynamics is key to improving their performance and efficiency, and this research significantly advances our theoretical understanding, paving the way for more efficient and powerful AI systems. Its exploration of meta-stable states opens up new avenues for research, potentially leading to more robust and reliable AI applications.
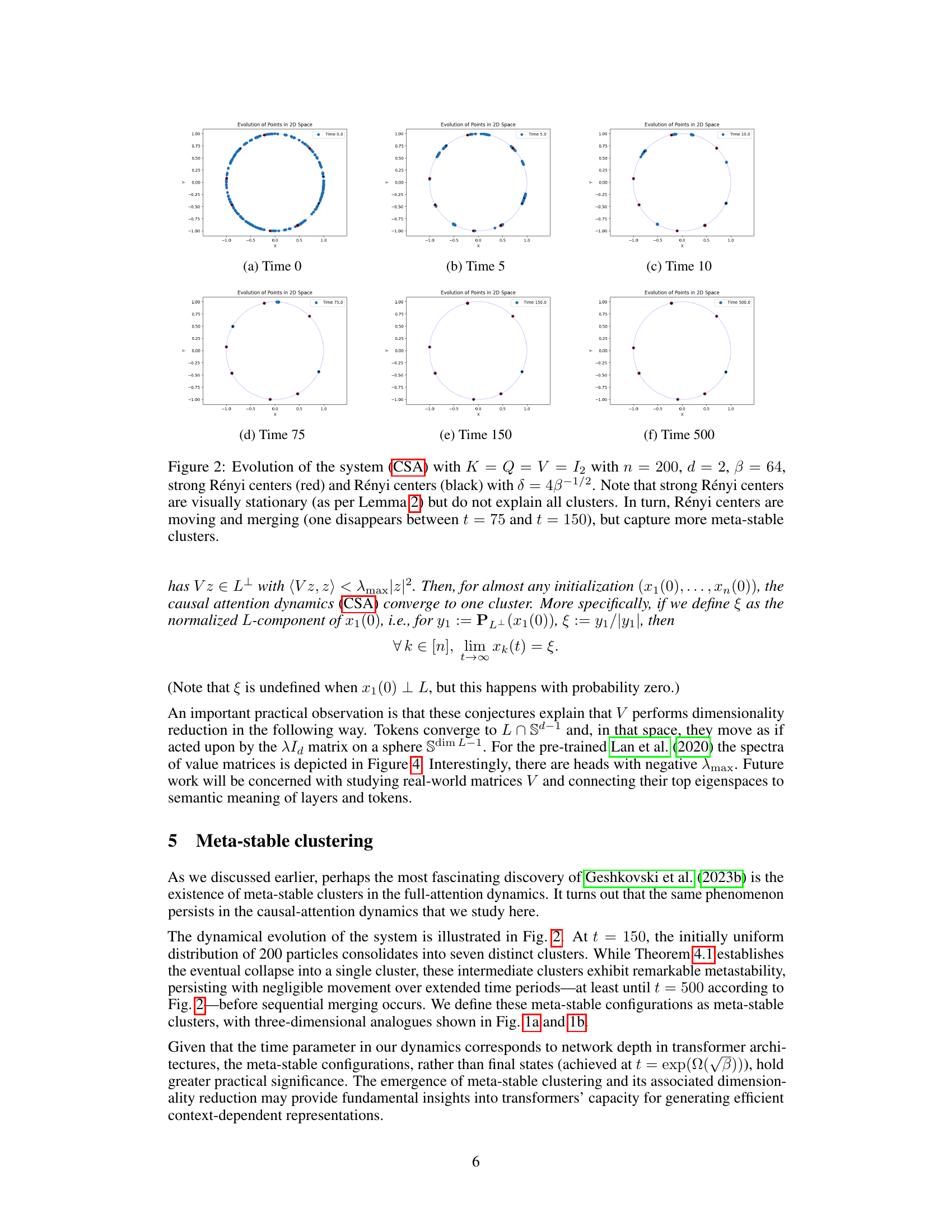
Visual Insights#

This figure shows the trajectories of particles representing tokens in a causal self-attention mechanism for different Value matrices (V). The Query and Key matrices (K and Q) are set to identity matrices. The other parameters used are temperature β = 9 and final time T = 5000. The initial positions of the 32 particles are randomly initialized on the unit sphere, and their final positions at time T are marked with red dots. The figure illustrates how the choice of Value matrix impacts particle clustering behavior, showing different final configurations ranging from a single cluster to multiple clusters.

This table summarizes the possible final configurations of particles in the causal self-attention model, depending on the largest eigenvalue (λmax) of the value matrix V and its multiplicity. The configurations range from a single point to multiple clusters, with the specific configuration determined by the interplay between the internal dynamics of individual tokens and their interactions through causal attention. The figure references correlate to visual representations of these configurations.
In-depth insights#
Causal Attention Flow#
A causal attention flow model would focus on the directionality of information processing in attention mechanisms. Unlike standard self-attention, where each token attends to all others simultaneously, a causal approach would restrict attention to only previous tokens in a sequence. This is crucial for generative tasks, as it prevents the model from ‘peeking’ into the future and ensures that the generated sequence is coherent and temporally consistent. The dynamics of such a system could be analyzed using interacting particle systems, where each token is a particle moving on a sphere based on its interactions with preceding tokens. This introduces the challenge of losing the convenient mean-field structure found in full-attention models but could potentially yield insights into the emergence of metastable states observed in numerical simulations, not easily explained by mean-field theory. Rigorous analysis of this system would involve proving convergence properties under various conditions on the key, query, and value matrices, with particular attention paid to the impact of the Value matrix’s eigenvalues on the final configuration of attention weights.
Clustering Dynamics#
The heading ‘Clustering Dynamics’ suggests an investigation into how data points or entities group together over time or across various conditions. A thoughtful analysis would explore the underlying mechanisms driving this clustering behavior, potentially involving force fields, inter-particle interactions, and asymptotic convergence. The paper might examine different scenarios, such as the emergence of meta-stable states where clusters form temporarily, and explore how certain parameters influence the clustering process. Mathematical models and simulations would likely play a central role in exploring the dynamics, with particular attention given to the characteristics of the final, stable cluster configurations. The overall aim is to gain a deeper understanding of the principles governing pattern formation and self-organization within complex systems.
Metastable States#
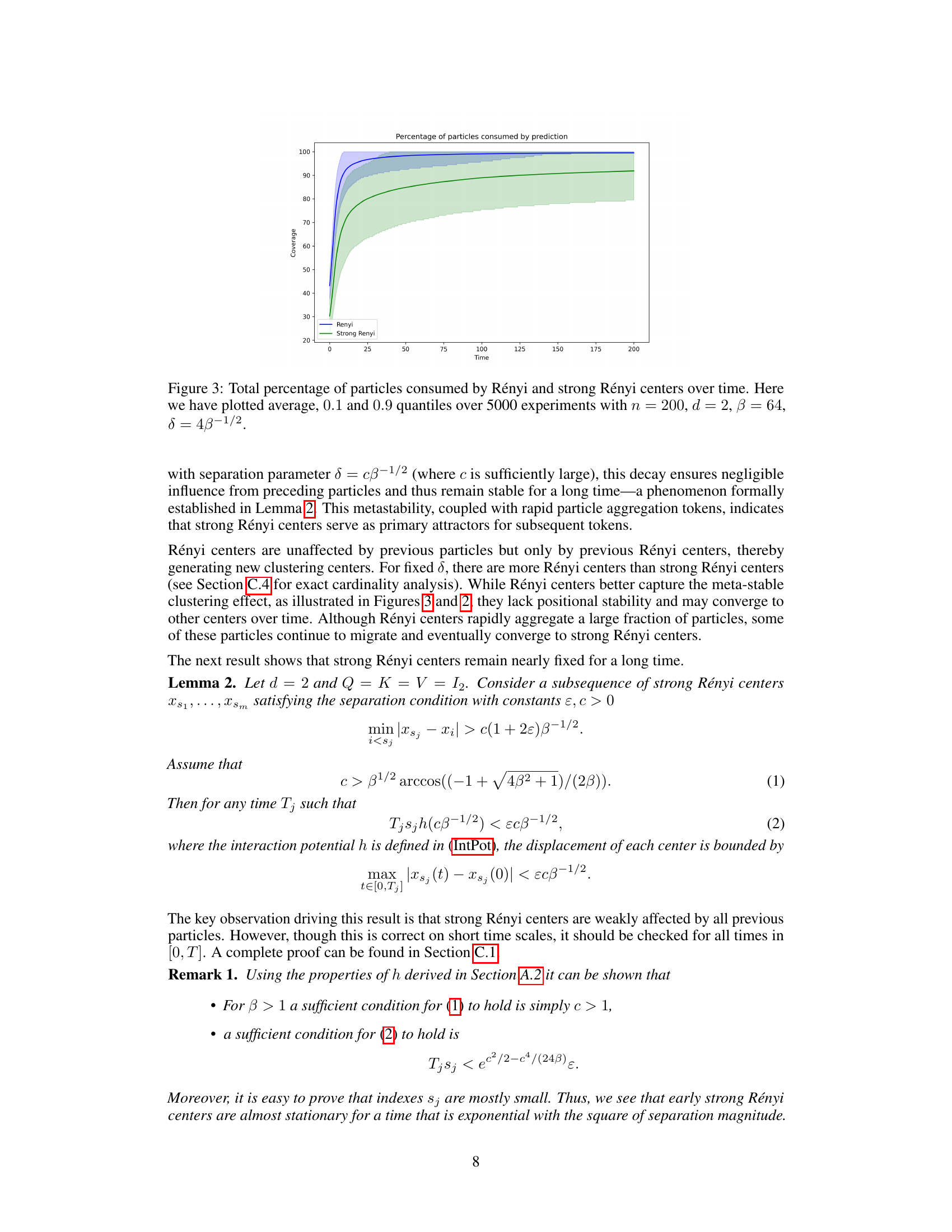
The concept of “Metastable States” in the context of the provided research paper refers to the intermediate, long-lived states exhibited by the interacting particle system modeling the self-attention mechanism in Transformers. These states, while not the final equilibrium, persist for extended periods, significantly impacting the overall dynamics of the model. The paper suggests that these metastable states are crucial for understanding the model’s ability to generate coherent sequences, as they represent a balance between individual token movements and collective clustering. Metastability is linked to the system’s high-dimensional nature, with the emergence of multiple clusters that ultimately coalesce into a single cluster, but only after a lengthy period. The theoretical framework provides insight into these metastable states by using the Rényi parking process as an analogy, which further underscores their complex structure and prolonged existence. The study of metastable states represents a significant challenge in theoretical analysis because of the difficulty in proving their existence and characterizing their properties.
Rényi Parking Analogy#
The Rényi parking problem analogy offers a fascinating lens through which to view the metastable clustering phenomenon observed in causal self-attention. The analogy highlights how the initial placement of tokens (particles), akin to cars randomly parking, determines the final configuration, a process governed by a balance of repulsive and attractive forces. The emergence of metastable states, where clusters persist for extended periods before merging, is directly linked to the spatial constraints imposed by prior token placements. Strong Rényi centers, analogous to the earliest parked cars in the problem, act as stable attractors, influencing the formation of persistent clusters and illustrating the lasting impact of initial conditions in shaping network behavior. This insightful analogy provides a theoretical framework for understanding metastable states, connecting the seemingly random dynamics of self-attention to the mathematically well-defined problem of Rényi parking, and paving the way for further investigations into the long-term evolution and stability of the system.
Future Directions#
Future research could explore several promising avenues. Extending the theoretical framework to encompass more realistic transformer architectures, including MLP layers and different normalization techniques, is crucial for bridging the gap between theoretical models and practical applications. Investigating the impact of various hyperparameters on meta-stable states and exploring methods for controlling the emergence and persistence of these states would provide deeper insights into the dynamics of attention. A rigorous mathematical treatment of meta-stable clustering, potentially drawing upon techniques from statistical physics and interacting particle systems, remains a significant challenge and would provide strong theoretical underpinnings to observed empirical phenomena. Furthermore, exploring the connection between the spectral properties of the value matrix and the semantic meaning of tokens and layers would offer valuable insights into the information processing capabilities of transformers.
More visual insights#
More on figures
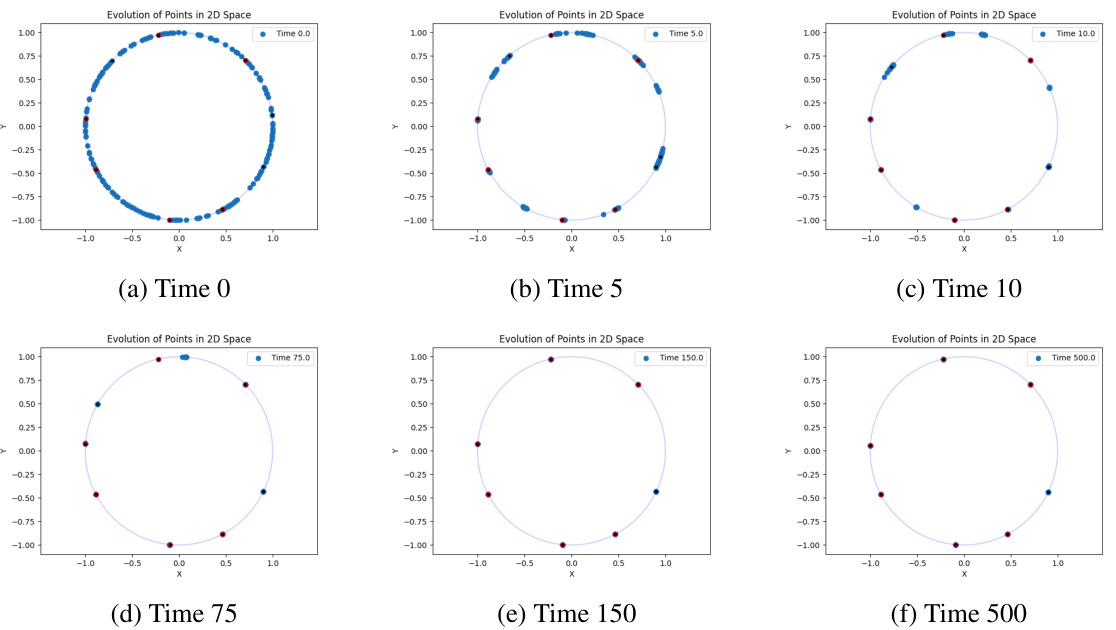
This figure visualizes the trajectories of particles for different value matrices in a causal self-attention transformer model. The trajectories are plotted on the surface of a sphere. Simple Query and Key matrices (identity matrices) and a temperature parameter (β=9) are used for all cases. The simulation runs until a final time T = 5000, with 32 particles initially distributed randomly across the sphere. Red dots indicate the final positions of the particles at time T. The figure demonstrates how different Value matrices affect the final clustering of particles, showing various scenarios including convergence to single points, a pair of antipodal points, and multiple clusters.
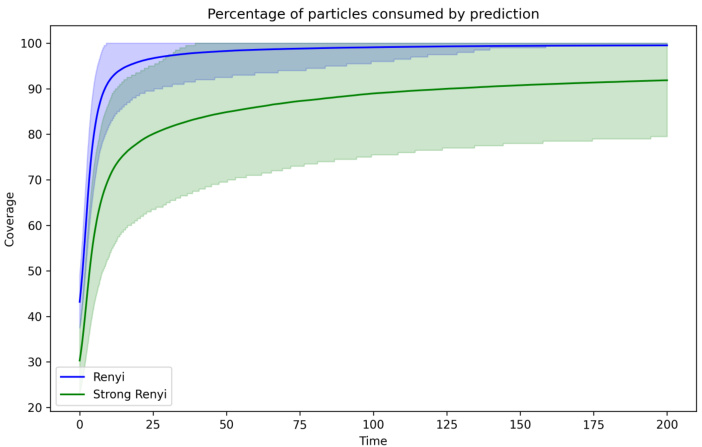
This figure shows the percentage of particles consumed by Rényi and strong Rényi centers over time. The data is averaged over 5000 experiments, and shows the average, 10th percentile, and 90th percentile for both Rényi and strong Rényi centers. The parameters used are n = 200 particles, dimension d = 2, temperature β = 64, and separation parameter δ = 4β-1/2. The plot demonstrates the increasing influence of the centers over time, particularly the strong Rényi centers, which appear to become more stable and consume a larger fraction of particles.
This figure shows the trajectories of particles (representing tokens) on a sphere for different value matrices (V) in a causal self-attention mechanism. The key and query matrices (K and Q) are kept as identity matrices, with a temperature parameter (β) of 9. The simulations run for 5000 time steps, starting from random initial positions on the sphere. The final positions of the particles at time T=5000 are indicated by red dots. The figure demonstrates how different value matrices affect the final clustering of particles.
Full paper#