↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Machine learning models often struggle with distribution shifts, where the training data differs significantly from real-world data. A key challenge is efficiently measuring this discrepancy. Current approaches are often computationally expensive or lack theoretical guarantees.
This paper tackles this challenge head-on. It introduces new, efficient algorithms for testing discrepancy, the measure of distance between training and test distributions. These algorithms are not only efficient but also provide strong theoretical guarantees, improving upon existing methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on distribution shift in machine learning because it provides efficient algorithms for discrepancy testing, a long-standing challenge. It offers universal learners that work across various test distributions, achieving near-optimal error rates, and offers new approaches and tools for analyzing distribution shift. These advancements are significant for improving the reliability of machine learning models in real-world applications where distribution shift is common.
Visual Insights#
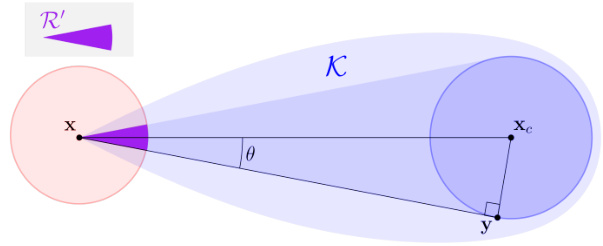
This figure illustrates a key geometric property of balanced convex sets used in the proof of Lemma E.12. It shows that if a point x lies within a balanced convex set K, then a substantial portion of a ball centered at x (B(x, ρ)) also lies within K. This is because a balanced convex set must contain a smaller ball (with non-negligible radius) somewhere within it. The diagram visually represents this by showing a cone (R’) within both the ball B(x, ρ) and the set K, highlighting the significant overlap.

This table presents new results on Testable Learning with Distribution Shift (TDS) learning using the L1 sandwiching technique. It compares the time complexity of TDS learning algorithms for two concept classes: degree-2 polynomial threshold functions (PTFs) and constant-depth circuits, highlighting exponential improvements compared to prior work which utilized L2 sandwiching. The table shows that the L1 sandwiching approach provides more efficient TDS learners, particularly for constant-depth circuits, where it achieves exponential improvements over previous methods.
In-depth insights#
Discrepancy Testing#
Discrepancy testing, a core concept in domain adaptation, assesses the difference between training and test data distributions. This is crucial because algorithms trained on one distribution may perform poorly on another. The paper explores efficient algorithms for discrepancy testing, focusing on a localized approach. This is computationally more feasible than global discrepancy testing, which considers all possible classifier pairs. The research makes significant strides in improving error guarantees, achieving near-optimal rates and providing universal learners that handle various test distributions. Polynomial-time testing is another key achievement, making the approach practical for large-scale applications. The techniques involve sandwiching polynomials and a novel notion of localized discrepancy. The work unifies and extends prior efforts on testable learning with distribution shifts, paving the way for more robust and reliable machine learning models in real-world scenarios where distribution shifts are common.
TDS Learning#
Testable Learning with Distribution Shift (TDS) learning presents a novel framework addressing the challenge of distribution shift in machine learning. It elegantly combines the traditional PAC learning model with a testing phase, ensuring that a learner’s output is only accepted if it performs well under an unseen test distribution, thus mitigating the risk of poor generalization due to distribution shift. The framework’s strength lies in its ability to provide certifiable error guarantees; if the test accepts, the learner’s hypothesis is guaranteed to achieve low error on the test distribution. The core of TDS learning lies in efficient discrepancy testing, focusing on algorithms capable of quickly determining whether the training and test distributions are sufficiently similar to warrant accepting the model’s predictions. This requires new algorithms, as existing methods for computing discrepancy are computationally intractable. Prior works had only addressed limited concept classes, but this paper generalizes these approaches considerably, proposing new, provably efficient algorithms for a broader range of function classes. Furthermore, this research introduces universal learners that guarantee acceptance under a wide range of test distributions rather than just those close to the training distribution, showcasing significant advancements in the field.
Universal Learners#
The concept of “Universal Learners” in machine learning signifies algorithms capable of adapting to a wide range of unseen data distributions. This contrasts with traditional models trained and evaluated on similar data; universal learners aim for robustness and generalization beyond the training environment. This robustness is especially crucial in real-world applications where data distributions are rarely static and often subject to unpredictable shifts. Achieving universality presents significant challenges, requiring algorithms to identify and leverage underlying structural properties of data, irrespective of specific distribution details. Success in this area would represent a major step toward building truly reliable and adaptable machine learning systems, as universal learners are less prone to overfitting or catastrophic failure when encountering unexpected input data. However, creating such learners necessitates careful consideration of computational complexity and theoretical guarantees.
Polynomial-Time Test#
The concept of a “Polynomial-Time Test” within a machine learning context signifies a crucial advancement in the efficiency and scalability of model evaluation. A polynomial-time test implies that the time required to validate a model’s performance on a given dataset scales polynomially with the size of the dataset. This is a significant improvement over exponential-time tests, which become computationally infeasible for large datasets. This efficiency is critical for deploying machine learning models in real-world applications, where datasets can be massive. The development of such tests often involves sophisticated techniques from theoretical computer science and algorithm design, such as carefully crafted algorithms or approximation methods which guarantee acceptable accuracy within a polynomial time constraint. The existence of a polynomial-time test has profound implications, particularly for scenarios involving model certification, safety, and robustness evaluation, making it a significant area of active research.
Future Directions#
The research paper’s “Future Directions” section could explore several avenues. Extending the theoretical framework to handle more complex concept classes beyond halfspaces and intersections is crucial. This could involve investigating the behavior of localized discrepancy in higher-dimensional spaces or with more intricate function families. Another direction is developing more sophisticated discrepancy testers. Current methods primarily focus on Gaussian marginals; exploring techniques for other distributions is needed for broader applicability. The runtime complexity of certain algorithms also needs addressing—developing fully polynomial-time algorithms for all concept classes is a key goal for practical application. Finally, empirical validation of the theoretical findings on real-world datasets is essential to demonstrate the effectiveness of proposed methods in handling distribution shifts. Such validation would assess the robustness and generalizability of the approaches.
More visual insights#
More on figures
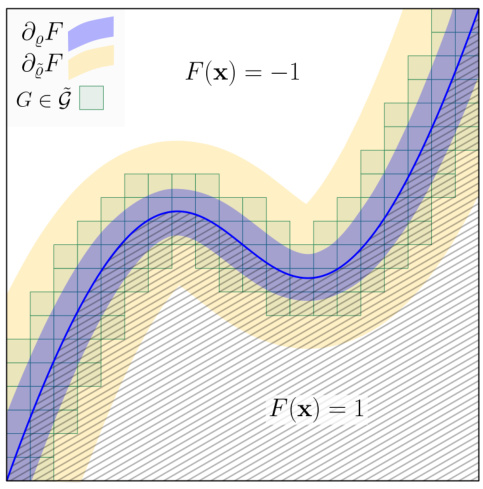
This figure illustrates how to discretize the disagreement region between two functions with smooth boundaries in order to obtain a localized discrepancy tester. The figure shows two functions, F and F, along with their respective boundaries. A grid is overlaid onto the region near the boundaries. The grid cells that have non-zero intersection with the disagreement region (shaded areas) are identified. The shaded regions show where the two functions disagree. By bounding the probability mass of these shaded areas, the discrepancy between the two functions can be bounded. This is achieved by bounding the probability of falling in each of the cells according to its size (proportionally to the region’s thickness) and the anti-concentration property.
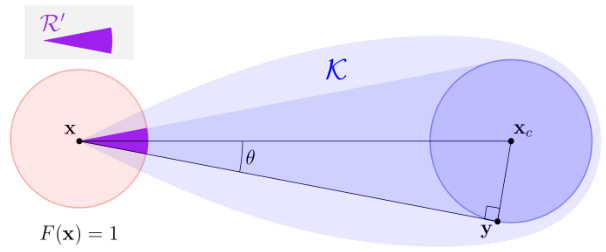
This figure illustrates the concept of local balancedness for convex sets. If a point x is inside a balanced convex set K, then a significant portion of the points in a small region around x (denoted by B(x, ρ)) are also in K. This is because a balanced convex set contains a ball of non-negligible radius, and the convex hull of x and this ball is a subset of K. The cone R’ visually represents the substantial portion of the neighborhood B(x, ρ) that lies within K, highlighting the concept of local balancedness.
More on tables
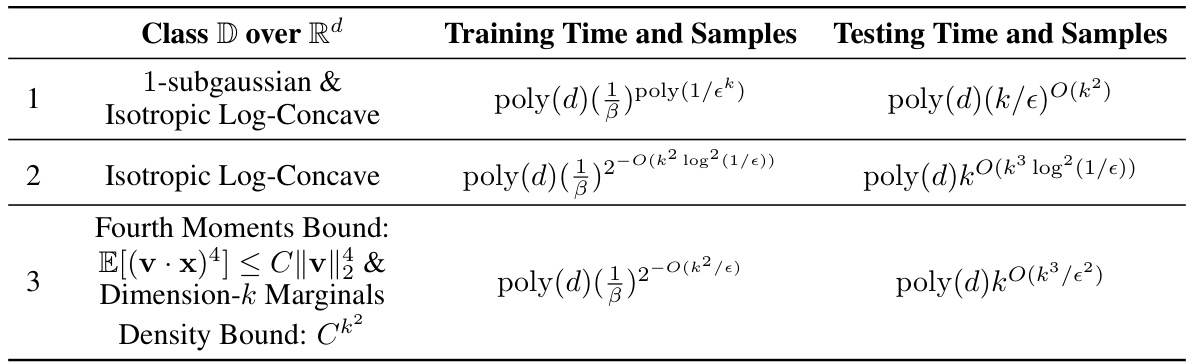
This table presents new results on Testable Learning with Distribution Shift (TDS) achieved using L1 sandwiching. It compares the time complexity of TDS learning algorithms for different concept classes (degree-2 polynomial threshold functions and circuits of size s and depth t) under different training marginal distributions (Gaussian and uniform). The table highlights the exponential improvement in runtime achieved using L1 sandwiching compared to previous work that used L2 sandwiching, particularly for constant-depth formulas and circuits.
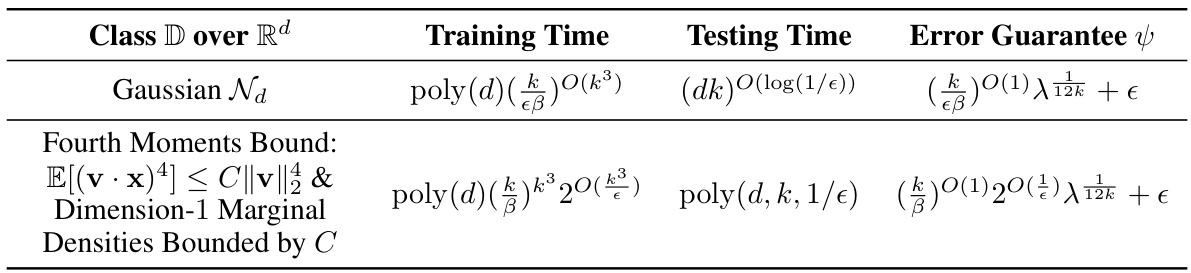
This table presents new results on Testable Distribution Shift (TDS) learning using L1 sandwiching. It shows significant improvements in runtime compared to previous work that used L2 sandwiching, particularly for constant-depth circuits. The table compares the training time and prior work for degree-2 polynomial threshold functions (PTFs) and circuits of size ’s’ and depth ’t’. Noteworthy is that the exponential runtime improvement for constant-depth circuits and the first TDS learning results for degree-2 PTFs are highlighted.
Full paper#



















