Shaping the distribution of neural responses with interneurons in a recurrent circuit model

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it provides a novel framework for understanding how neural circuits shape the distribution of neural responses. This is a fundamental question in neuroscience, with implications for our understanding of sensory processing, information processing, and learning. The model’s use of optimal transport and its application to natural image statistics provides a new approach for studying these complex processes and could lead to advances in artificial neural networks.

Visual Insights

#

This figure schematically shows a recurrent neural circuit model with two primary neurons and three interneurons. The left panel shows the distribution of 2D input signals. The center panel depicts the circuit architecture, illustrating how primary neurons receive feedforward input and recurrent feedback from interneurons. An inset highlights the processing within a single interneuron. The right panel displays the resulting distribution of 2D circuit responses after processing by the circuit.

In-depth insights

#

Optimal Transport

#

Optimal transport, in the context of this research, offers a powerful framework for understanding how neural circuits transform sensory inputs into neural representations. The core idea is to view this transformation as an optimal mapping between input and output distributions. This mapping minimizes a cost function, representing the ‘distance’ or difference between the input and the desired output distribution (e.g., a Gaussian distribution promoting efficient coding). The model elegantly connects a biological objective—maximizing information transmission—with a mathematical optimization problem. By formulating the problem within the framework of optimal transport, the authors create a powerful mathematical tool to analyze circuit behavior and learn the parameters (synaptic weights, activation functions) that optimize the transformation. This approach provides a bridge between neural circuit structure and function and information-theoretic principles of efficient coding. Importantly, this normative framework allows for the analysis of nonlinear transformations, in contrast to previous approaches that focused primarily on linear operations, thereby enabling the investigation of biologically plausible nonlinearities inherent in neural circuits.

Interneuron Control

#

Interneuron control mechanisms are crucial for shaping neural circuit activity and information processing. Local interneurons dynamically adjust synaptic connections and activation functions, influencing the overall response distribution of the circuit. This control is not merely linear but demonstrably nonlinear, enabling complex transformations of input signals. The paper highlights the importance of these normative mechanisms, suggesting how interneurons optimize information transmission and efficiency, potentially by minimizing statistical dependencies in neural responses. The model presented provides a strong theoretical framework for understanding how interneurons directly and systematically control neural response distributions. Adjustment of interneuron connectivity and activation functions provides a flexible mechanism for shaping circuit output, revealing a powerful and nuanced aspect of neural computation.

Natural Image Stats

#

The study of natural image statistics plays a crucial role in understanding visual perception and building efficient computational models of the visual system. Natural images exhibit non-random statistical properties, such as correlations between neighboring pixels and the prevalence of certain edge orientations. These regularities are exploited by the visual system to improve efficiency. For example, the redundancy reduction hypothesis posits that sensory systems transform natural signals to minimize or eliminate statistical dependencies between neural responses, making the representation more efficient. This relates to the concept of sparse coding, which suggests that natural images can be efficiently represented by a small number of activated neurons. By characterizing the statistical structure of natural scenes, we gain a better understanding of how the visual system processes and represents information, revealing insights into the design principles of biological vision. Moreover, understanding natural image statistics aids in developing and evaluating computer vision algorithms, leading to improved performance and efficiency in applications like image compression, object recognition, and image generation.

Nonlinear Dynamics

#

The concept of ‘Nonlinear Dynamics’ in the context of neural networks is crucial because it acknowledges that the relationship between neural activity and its effects isn’t straightforward. Linear models, while simpler, fail to capture the complexity of biological systems where interactions are often multiplicative or involve thresholds. Nonlinear dynamics introduce factors like feedback loops, oscillations, and bifurcations, leading to emergent behavior that isn’t predictable from individual neuron responses. This has important implications for information processing. Nonlinearity allows for more efficient encoding of information by leveraging the rich range of dynamic patterns that neural systems can generate. Furthermore, the adaptability of neural networks is partially explained by their capacity to reorganize their dynamical repertoire in response to environmental changes. Understanding nonlinear dynamics in neural circuits is key to deciphering how brains learn, adapt, and make decisions, ultimately pushing the boundaries of AI through the development of more biologically realistic and efficient models.

Circuit Learning

#

The concept of ‘Circuit Learning’ in the context of neural network research is fascinating. It suggests a move beyond simply training individual neural networks towards adapting entire neural circuits. This involves not just modifying connection weights but also potentially altering the structure, or even the types of neurons involved, within the circuit. This could involve exploring mechanisms such as synaptic plasticity, where connections strengthen or weaken based on activity patterns, and interneuron adaptation, where the function and responsiveness of inhibitory neurons may change. Efficient coding theories would also be central to this line of research, seeking to understand how circuits optimize information transfer while accounting for biological constraints like energy consumption. A key area of investigation would be developing normative models to compare the circuit’s performance to an optimal system to see how well circuits match what would be theoretically predicted. Optimal transport theory could provide a valuable mathematical framework. The insights from ‘Circuit Learning’ would have significant implications for building more powerful and biologically realistic artificial intelligence systems and gaining a deeper understanding of the brain’s remarkable computational abilities.

More visual insights

#

More on figures

This figure schematically depicts a recurrent neural circuit model comprising two primary neurons and three interneurons. The left panel shows the input signal distribution, the center panel illustrates the circuit architecture with feedforward and feedback connections between primary and interneuron populations, and the right panel displays the target response distribution. The inset highlights the internal workings of a single interneuron, illustrating how it receives weighted input, processes this via an activation function, and produces a scaled output that feeds back to the primary neurons.

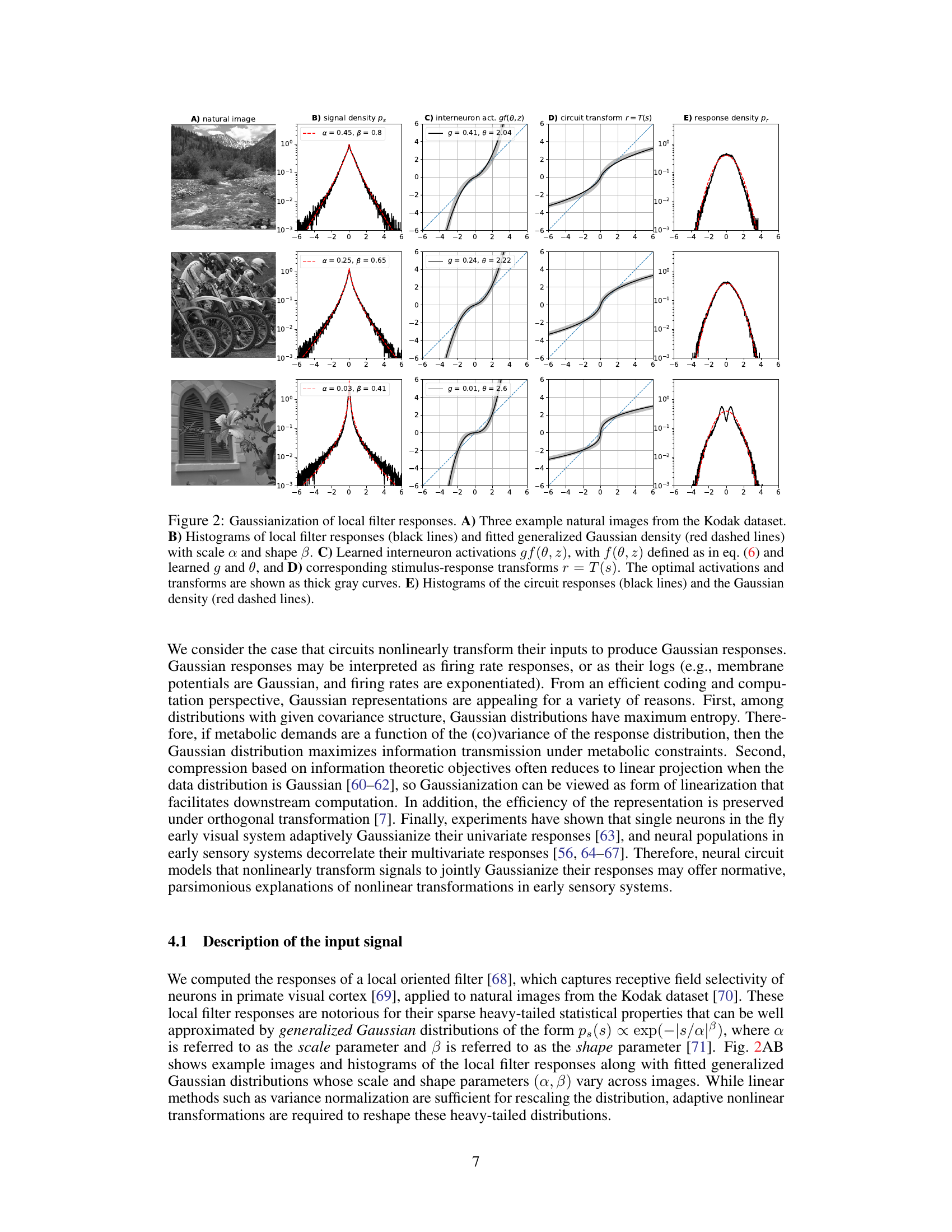
This figure demonstrates the Gaussianization of local filter responses through the learned circuit transformation. It shows three examples of natural images (A), their corresponding local filter response histograms with generalized Gaussian fits (B), the learned interneuron activation functions (C), the learned stimulus-response transformations (D), and finally the histograms of the circuit responses showing near-Gaussian distributions (E). Each row represents a different image with varying parameters α and β illustrating the model’s adaptation to diverse input statistics.

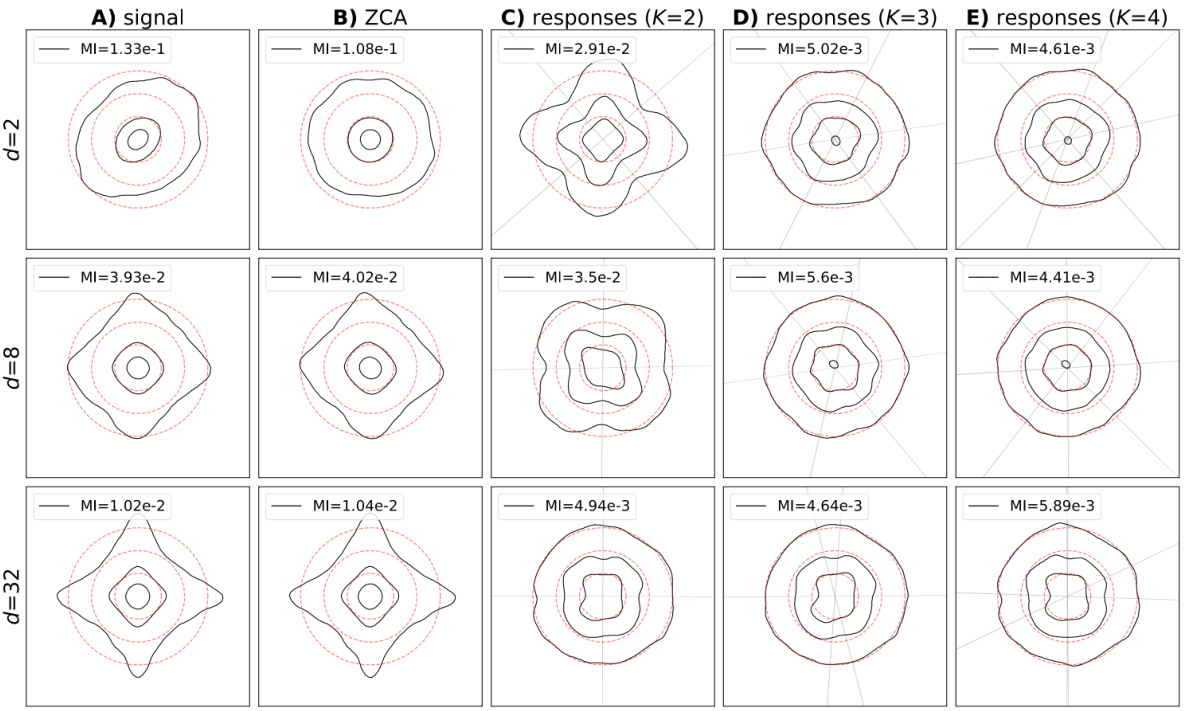
This figure visualizes the effect of the proposed algorithm on pairs of local filter responses at different spatial offsets (d=2, 8, 32). It compares the original responses (A), ZCA-whitened responses (B), and responses generated by the model with different numbers of interneurons (C-E). The contours represent the probability density, illustrating how the algorithm transforms the data towards a spherical Gaussian distribution. Mutual information values quantify the reduction in statistical dependencies between the response coordinates.

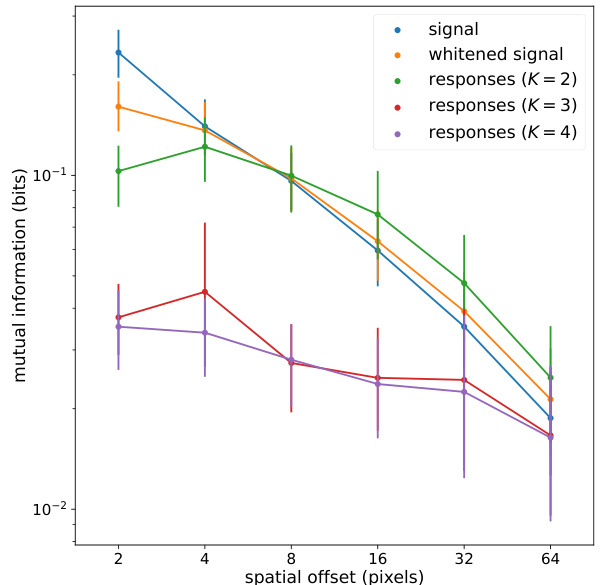
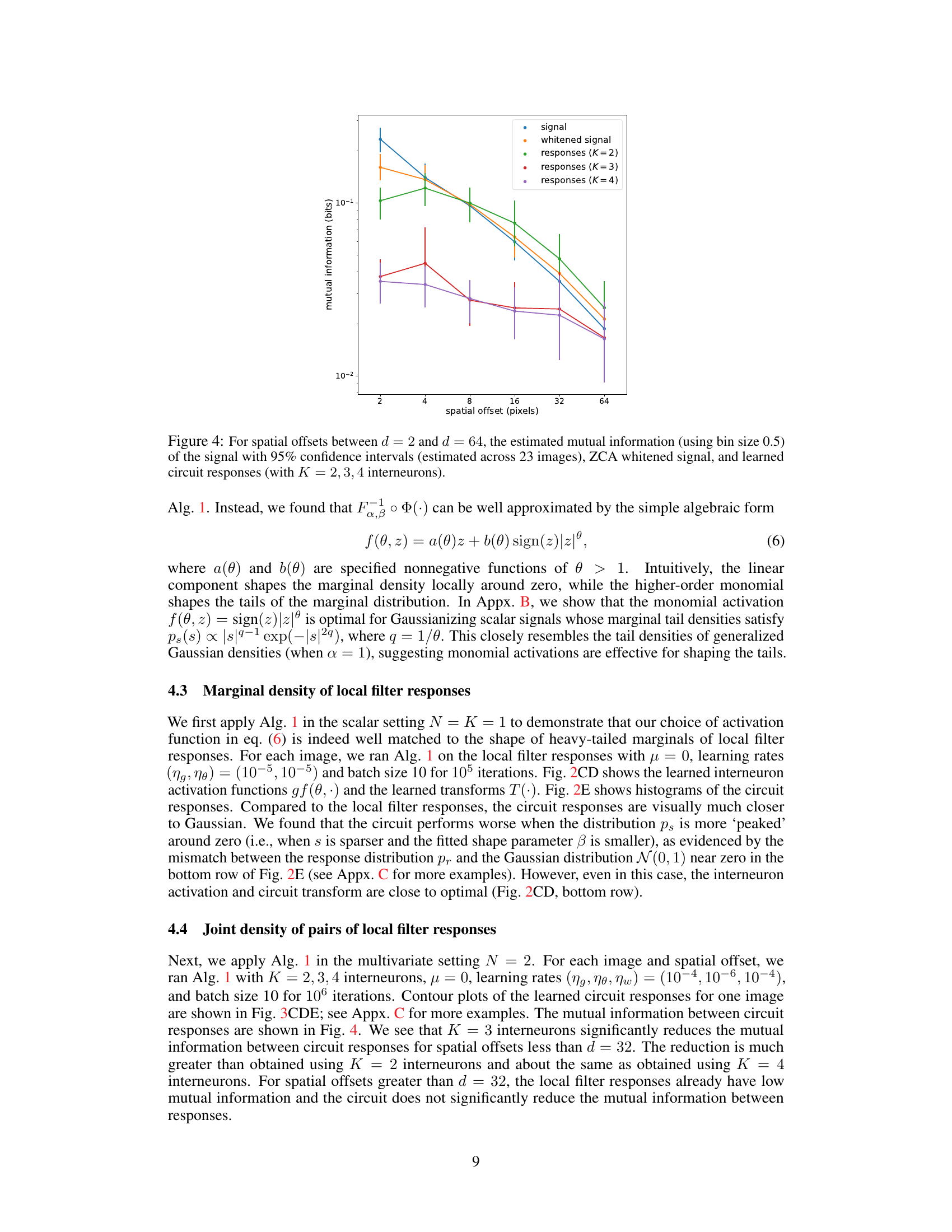
This figure shows how mutual information between pairs of local filter responses changes with spatial offset. It compares the original signal, the signal after ZCA whitening, and the signals processed by the neural circuit model with varying numbers of interneurons (K=2, 3, and 4). The results demonstrate the circuit’s ability to reduce statistical dependencies between neural responses.

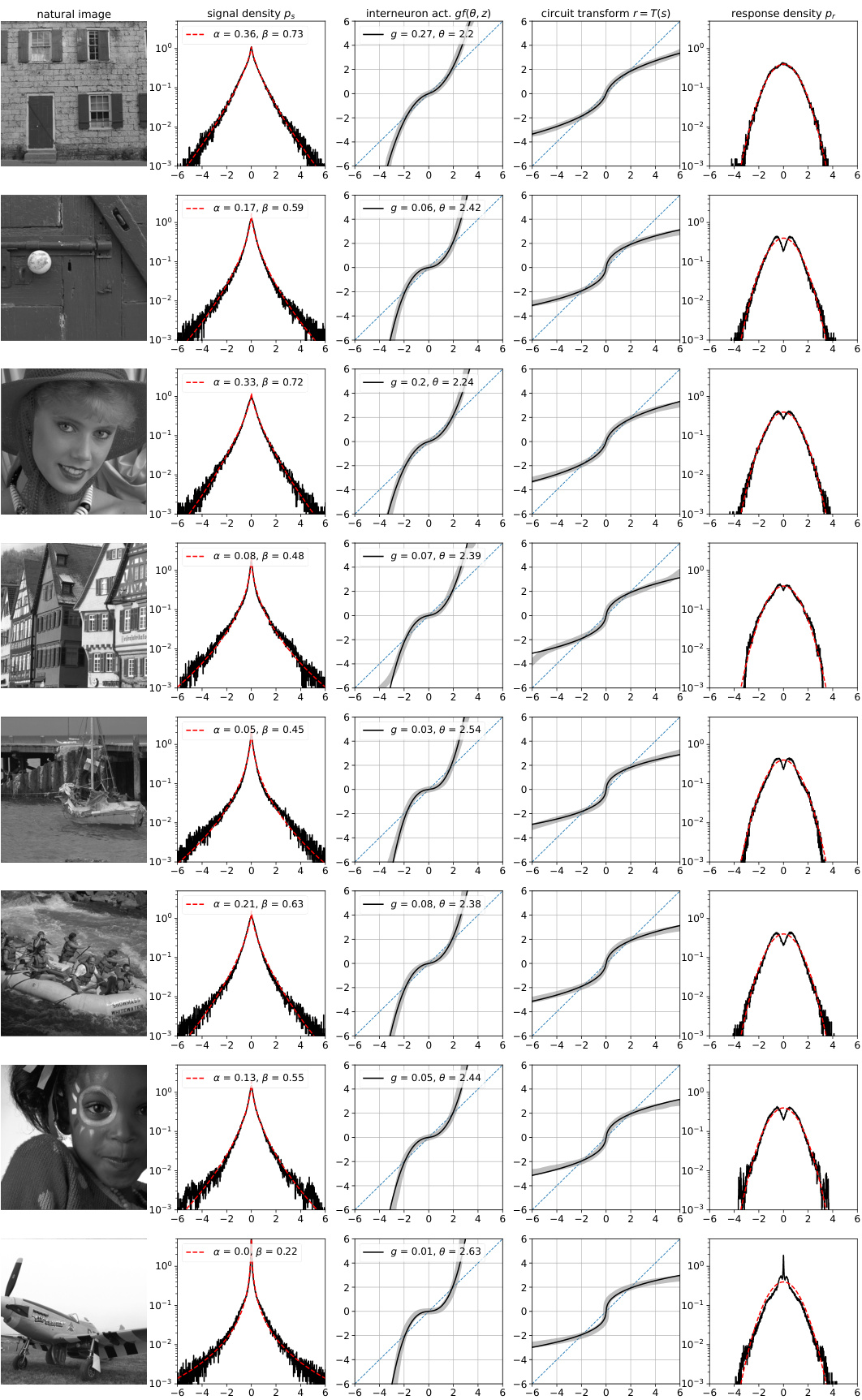
This figure demonstrates the Gaussianization process achieved by the model. It shows three example images (A), their corresponding local filter response histograms compared with fitted generalized Gaussian densities (B), the learned interneuron activation functions (C), the learned stimulus-response transformations (D), and finally, histograms of the circuit responses compared with the Gaussian density (E). The goal is to show how the model transforms the input distribution (heavy-tailed) into a Gaussian distribution.

This figure shows contour plots visualizing the distribution of local filter responses for different spatial offsets (d=2, 8, 32). It compares the original signal distribution, ZCA-whitened responses, and the circuit’s learned responses using 2, 3, and 4 interneurons. The mutual information between coordinates is quantified for each case, demonstrating the effect of the circuit in reducing statistical dependencies.

Full paper

#