↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Reinforcement learning (RL) often uses policy gradient methods, with Policy Mirror Descent (PMD) being a prominent example. However, traditional PMD methods often struggle with slow convergence and limited scalability. They typically rely on 1-step greedy policy updates, which might not be optimal. This limits their performance, especially in complex environments.
To address these challenges, the authors introduce h-PMD, an improved version of PMD that uses multi-step greedy policy updates with lookahead. This enhancement leads to significantly faster convergence and better sample efficiency. The paper also extends this approach to handle large state spaces using function approximation, further improving its applicability and practicality. The theoretical findings are supported by empirical results.
Key Takeaways#
Why does it matter?#
This paper is crucial for RL researchers because it significantly improves the convergence rate of policy mirror descent (PMD) algorithms by incorporating multi-step greedy policy improvement with lookahead. This enhancement offers faster convergence, improved sample complexity, and scalability to large state spaces, advancing the state-of-the-art in PMD and its applications.
Visual Insights#
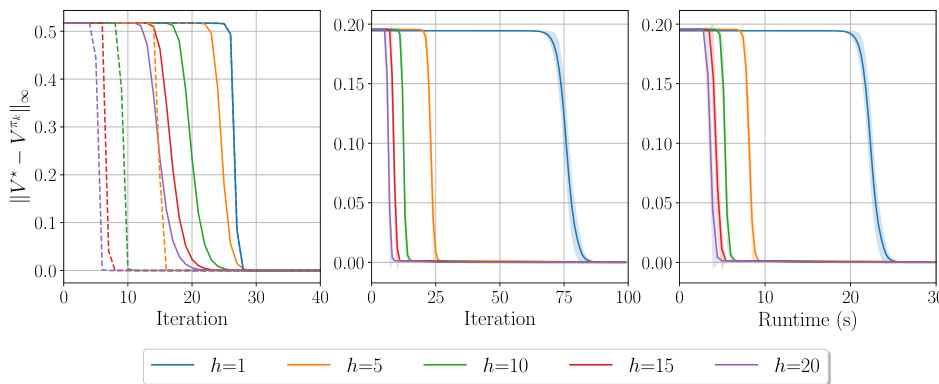
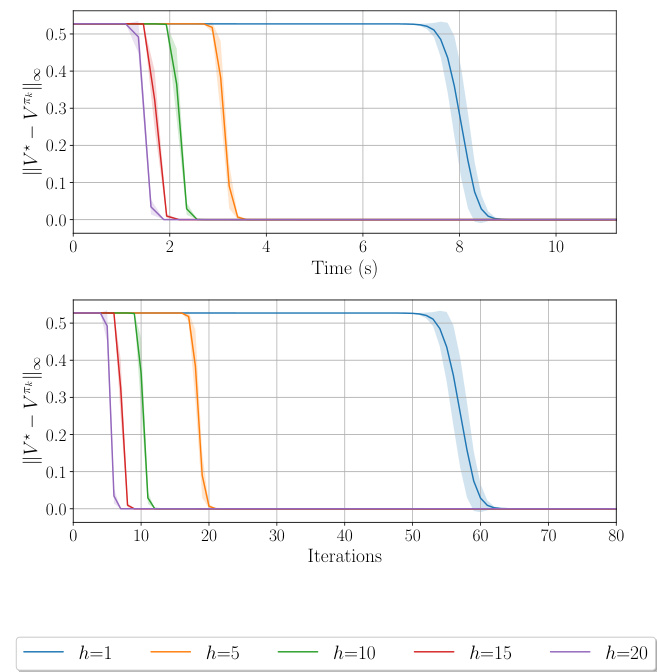
This figure shows the suboptimality gap of the h-PMD algorithm in both exact and inexact settings. The x-axis represents iterations for the exact case and both iterations and runtime for the inexact case. The y-axis represents the suboptimality gap. The figure shows that h-PMD converges faster with larger h, even considering runtime. The different line styles represent different step size strategies, either adaptive or fixed.

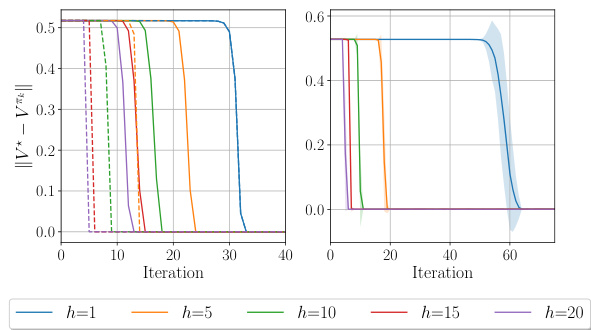
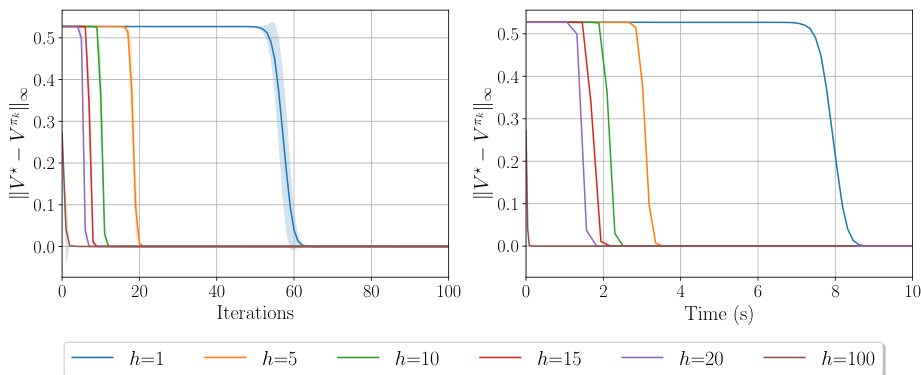
This figure shows the training curves for the PMD-MCTS algorithm on two bsuite environments, Catch and DeepSea, for various lookahead depths (h). The left panel displays the Catch environment, and the right panel shows the DeepSea environment. The x-axis represents training time in seconds, and the y-axis represents the reward. Each line represents a different lookahead depth. The key observation is that a lookahead depth of 1 fails to converge within a reasonable number of iterations for both environments. The figure demonstrates the effectiveness of lookahead in improving algorithm performance.
In-depth insights#
h-PMD Algorithm#
The core contribution of this paper revolves around the introduction and analysis of the h-PMD algorithm. h-PMD enhances the standard Policy Mirror Descent (PMD) framework by incorporating a multi-step lookahead mechanism, significantly improving its convergence rate. Instead of performing a single greedy policy update, h-PMD performs h such updates, thereby considering the consequences of actions across a longer horizon. This approach is inspired by successful RL techniques such as AlphaGo and AlphaZero, which demonstrated the superior performance of multi-step lookahead strategies. The authors rigorously analyze h-PMD, proving faster dimension-free convergence contingent on the computation of multi-step greedy policies. Importantly, they also address the computational challenge of computing multi-step lookahead policies by introducing an inexact version that leverages Monte Carlo sampling, thus making the method more scalable. The analysis provides sample complexity bounds showing improved efficiency compared to existing methods. Furthermore, the paper extends its results to function approximation scenarios, facilitating the application of h-PMD to larger state spaces. Overall, the h-PMD algorithm offers a valuable enhancement to the PMD family, providing a more efficient and scalable approach for reinforcement learning problems.
Lookahead’s Impact#
The concept of ’lookahead’ significantly enhances reinforcement learning algorithms by improving the quality of policy updates. Instead of myopically optimizing for immediate rewards, lookahead methods consider the consequences of actions several steps into the future. This multi-step perspective allows for more informed decisions, potentially leading to faster convergence and better overall performance. However, the computational cost of lookahead increases exponentially with the planning horizon. This trade-off between improved policy quality and increased computational demands necessitates a careful evaluation of the optimal lookahead depth for specific applications. The effectiveness of lookahead is also contingent on the accuracy of future value estimations, which often require sophisticated prediction models, such as Monte Carlo methods or tree search, further influencing the efficiency of the approach. Ultimately, the incorporation of lookahead offers a powerful strategy for enhancing RL algorithms but requires meticulous consideration of the inherent computational and estimation challenges.
Inexact h-PMD#
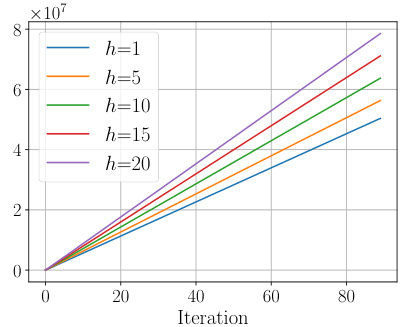
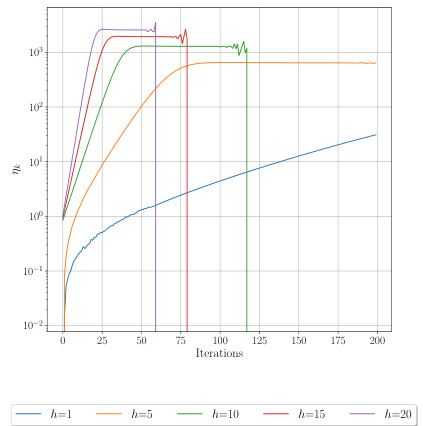
The section ‘Inexact h-PMD’ addresses the practical limitations of the h-PMD algorithm when exact computation of multi-step lookahead values is infeasible. This is crucial because exact computation becomes computationally prohibitive as the lookahead depth (h) increases. The authors acknowledge this constraint and propose a solution using Monte Carlo sampling to estimate the unknown h-step action-value functions. This inexact version introduces stochasticity into the algorithm but allows for scalability to larger problems. The section likely details the Monte Carlo estimation procedure, providing an analysis of its sample complexity, demonstrating how many samples are required for accurate estimations with varying levels of lookahead and confidence levels. Importantly, it’s likely shown that the sample complexity improves with increasing h, offsetting the increased computational demand of a larger lookahead. This highlights a tradeoff between computational cost and estimation accuracy. The discussion likely compares the inexact h-PMD’s performance and convergence guarantees to its exact counterpart and possibly other state-of-the-art RL algorithms, demonstrating its effectiveness in practical settings. Ultimately, the inexact h-PMD section provides a robust and scalable solution, bridging the gap between theoretical elegance and real-world applicability.
Function Approx#
The heading ‘Function Approx’ likely refers to a section detailing the use of function approximation techniques within a reinforcement learning (RL) algorithm. This is crucial for scaling RL to complex environments with large state spaces, where tabular methods become intractable. Function approximation replaces the need to store and update values for every state-action pair, instead using a parameterized function (e.g., a neural network) to approximate the value or Q-function. The paper likely discusses the choice of approximation architecture, the impact of approximation error on algorithm convergence, and perhaps strategies to mitigate these errors (e.g., using a generative model to improve sample efficiency). A key aspect is the trade-off between approximation accuracy and computational cost. More accurate approximations may lead to better policy performance but increase computational complexity. The discussion might also address the effect of the chosen approximation method on the algorithm’s convergence rate and sample complexity, showing whether the theoretical guarantees from the tabular setting still hold or need to be adapted in this approximate setting. Results might demonstrate the successful application of function approximation, allowing the RL algorithm to operate in high-dimensional state spaces while maintaining satisfactory performance and potentially outperforming tabular methods in terms of sample efficiency.
Future Works#
The paper’s conclusion suggests several promising avenues for future research. Extending the h-PMD algorithm to handle more complex function approximation methods, beyond linear models, is a key area. This would allow scaling to even larger state spaces and more intricate problem domains. Investigating the use of more sophisticated exploration mechanisms is crucial for improving the algorithm’s performance in challenging environments. The current approach relies on a balance between exploitation and exploration, but more advanced methods could enhance efficiency. Adaptive strategies for selecting the lookahead depth (h) could significantly improve practical performance, as the optimal choice of h might vary depending on the problem’s characteristics. A deeper examination of the tradeoff between computational cost and convergence rate associated with h is needed. Finally, a comparative analysis against other state-of-the-art algorithms on benchmark problems would bolster the paper’s conclusions and offer further insights into the algorithm’s strengths and weaknesses.
More visual insights#
More on figures
This figure compares the performance of the h-PMD algorithm in both exact and inexact settings across different values of h (lookahead depth). The left panel shows the suboptimality gap against iterations for the exact setting. The middle and right panels display the same metrics for the inexact setting, with the right panel also showing runtime. The results indicate that higher values of h lead to faster convergence, even considering runtime.
This figure shows the suboptimality gap for h-PMD in both exact and inexact settings. The left plot shows the exact setting, with the suboptimality plotted against iterations. The middle and right plots show the inexact setting, with suboptimality plotted against both iterations and runtime. The results show that h-PMD converges faster with larger lookahead depths (h), even considering the increased computational cost per iteration. Different step-size strategies were used, with the results highlighting the benefits of lookahead regardless of the step-size approach.
This figure shows the convergence performance of the h-PMD algorithm in both exact and inexact settings. The left panel displays the suboptimality gap versus iterations for the exact setting, illustrating that higher lookahead depth (h) leads to faster convergence. The middle and right panels show the same metrics for the inexact setting, with the right panel additionally showing runtime. Different step-size schedules are compared (dotted and solid lines). The results consistently demonstrate the benefits of lookahead, showing faster convergence with increasing h, even when considering runtime.
This figure compares the performance of the h-PMD algorithm in both exact and inexact settings. The left plot shows the suboptimality gap against iterations for the exact h-PMD (where the value function can be computed exactly), demonstrating faster convergence with increasing lookahead depth (h). The middle and right plots show the same for the inexact h-PMD (where the value function is estimated using Monte Carlo sampling), with the right plot showing the runtime instead of iterations. The results show h-PMD converges faster with higher h, even when considering runtime.
This figure displays the suboptimality gap (difference between optimal value function and the value function at each iteration) for h-PMD in both exact (where h-step lookahead values are computed precisely) and inexact (where h-step lookahead values are estimated using Monte Carlo sampling) settings. The left panel shows iterations vs. suboptimality gap in the exact setting, while the middle and right panels show iterations and runtime vs. suboptimality gap in the inexact setting. The figure shows that h-PMD with higher values of lookahead parameter h converges faster, even when considering runtime (right panel). Two different step size strategies are also compared.
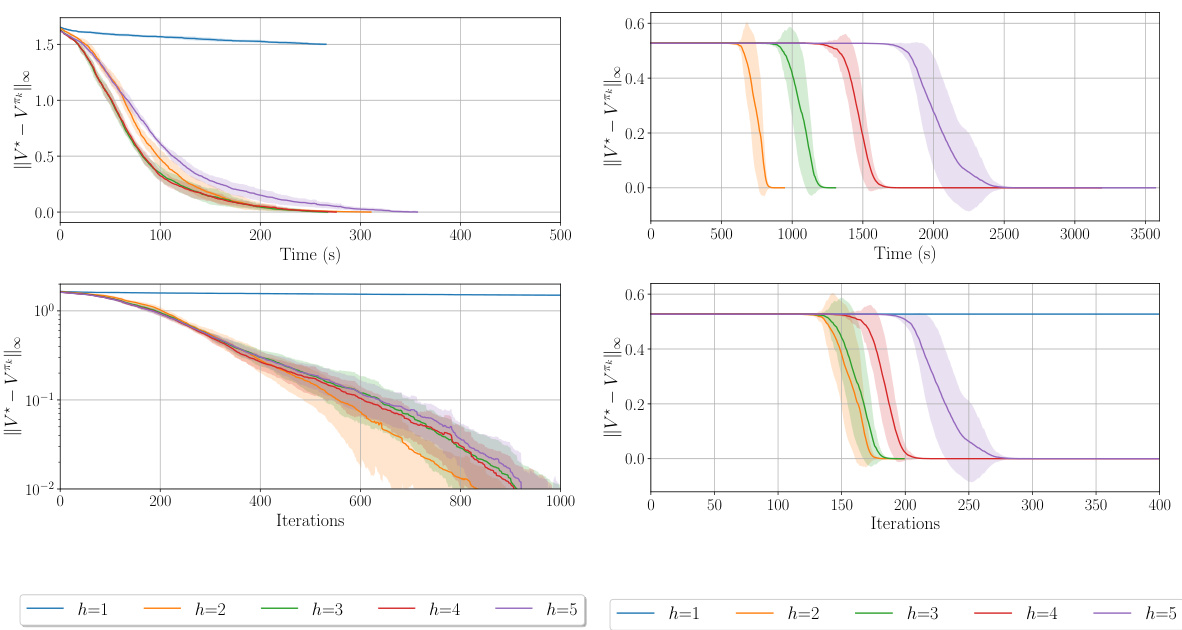
This figure shows the convergence rate of the h-PMD algorithm (in both exact and inexact settings) for different lookahead depths (h). The left plot shows the suboptimality gap against the number of iterations for the exact setting, while the middle and right plots show this gap against the number of iterations and the runtime respectively for the inexact setting. The plots demonstrate that increasing the lookahead depth (h) leads to faster convergence, even when considering the increased computational cost per iteration.
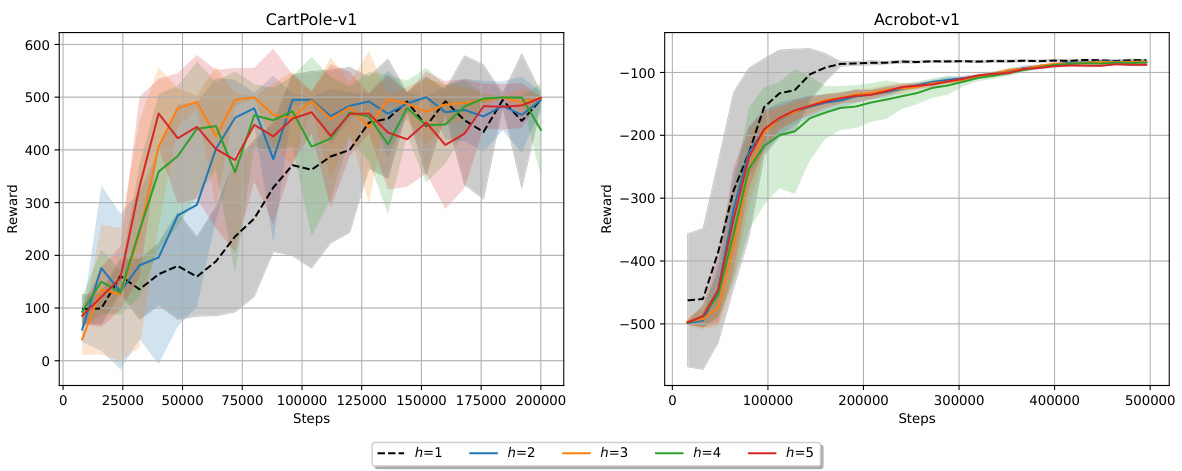
This figure shows the performance of h-PMD on two continuous control environments from OpenAI Gym: CartPole-v1 and Acrobot-v1. The x-axis represents the total number of steps (and therefore samples) taken by the algorithm, while the y-axis shows the accumulated reward. Different line colors represent different lookahead depths (h). The shaded areas represent confidence intervals. The results demonstrate that increasing the lookahead depth (h) can improve performance in the CartPole environment, but the effect is less pronounced and potentially non-monotonic in the Acrobot environment, highlighting task-dependent behavior of the lookahead mechanism.
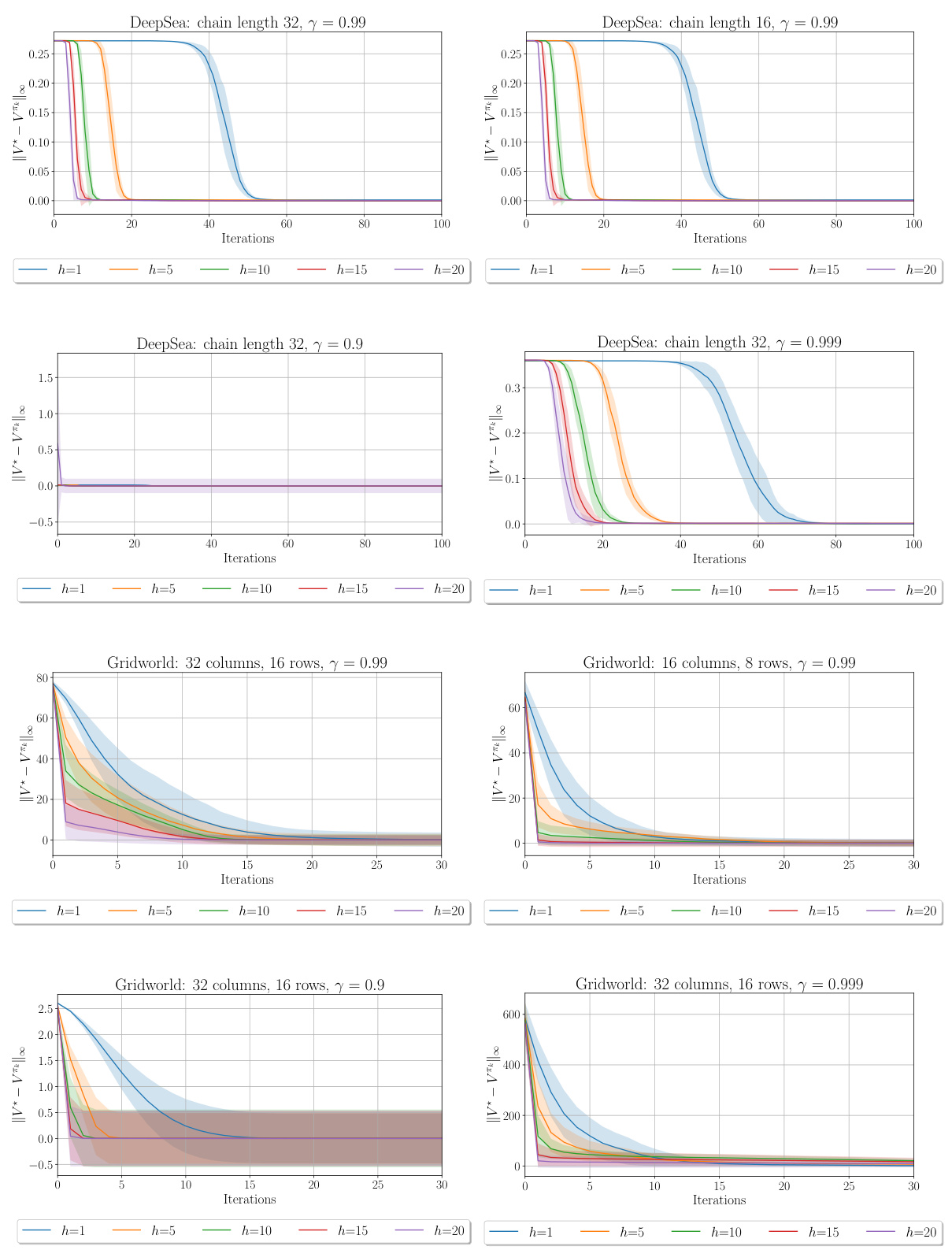
The figure shows the convergence performance of the h-PMD algorithm in both exact and inexact settings. The left panel displays the suboptimality gap against the number of iterations for the exact case, while the middle and right panels show the same metric against iterations and runtime respectively for the inexact case. The results indicate that increasing the lookahead depth h leads to faster convergence, even considering the increased computational cost in the inexact setting.
Full paper#