TL;DR#
Many machine learning models aim to produce well-calibrated probabilistic predictions. However, ensuring fairness requires these predictions to be calibrated across multiple subgroups, a property known as multicalibration. Achieving this through post-processing can be computationally expensive and sensitive to hyperparameter selection, as well as dataset size. Existing theoretical research often focuses on idealized settings.
This research paper presents a large-scale empirical study investigating the effectiveness of multicalibration post-processing across diverse datasets and models. The study compares various methods including standard empirical risk minimization (ERM), classical recalibration methods, and explicit multicalibration algorithms. The findings reveal that models already well-calibrated often achieve multicalibration implicitly. While post-processing can improve poorly-calibrated models, it’s crucial to carefully tune hyperparameters, and it’s often surprisingly less effective than traditional methods.
Key Takeaways#
Why does it matter?#
This paper is crucial because it bridges the gap between theoretical multicalibration and its practical application in various machine learning models. The comprehensive empirical study and released Python package provide valuable insights and tools for researchers across diverse fields, particularly in fairness-related areas. The findings challenge existing assumptions and open new avenues for algorithm development and hyperparameter tuning in multicalibration.
Visual Insights#

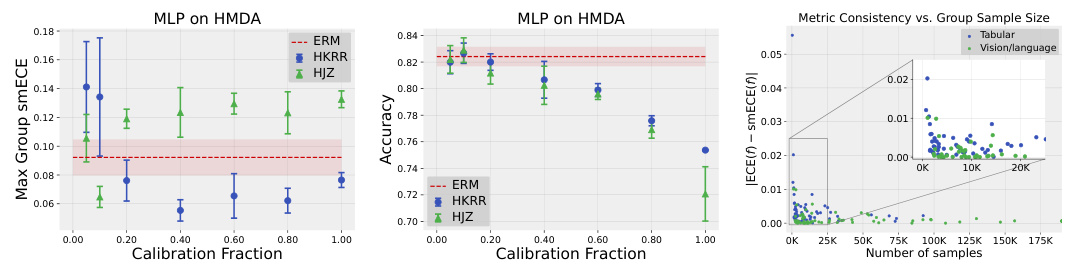
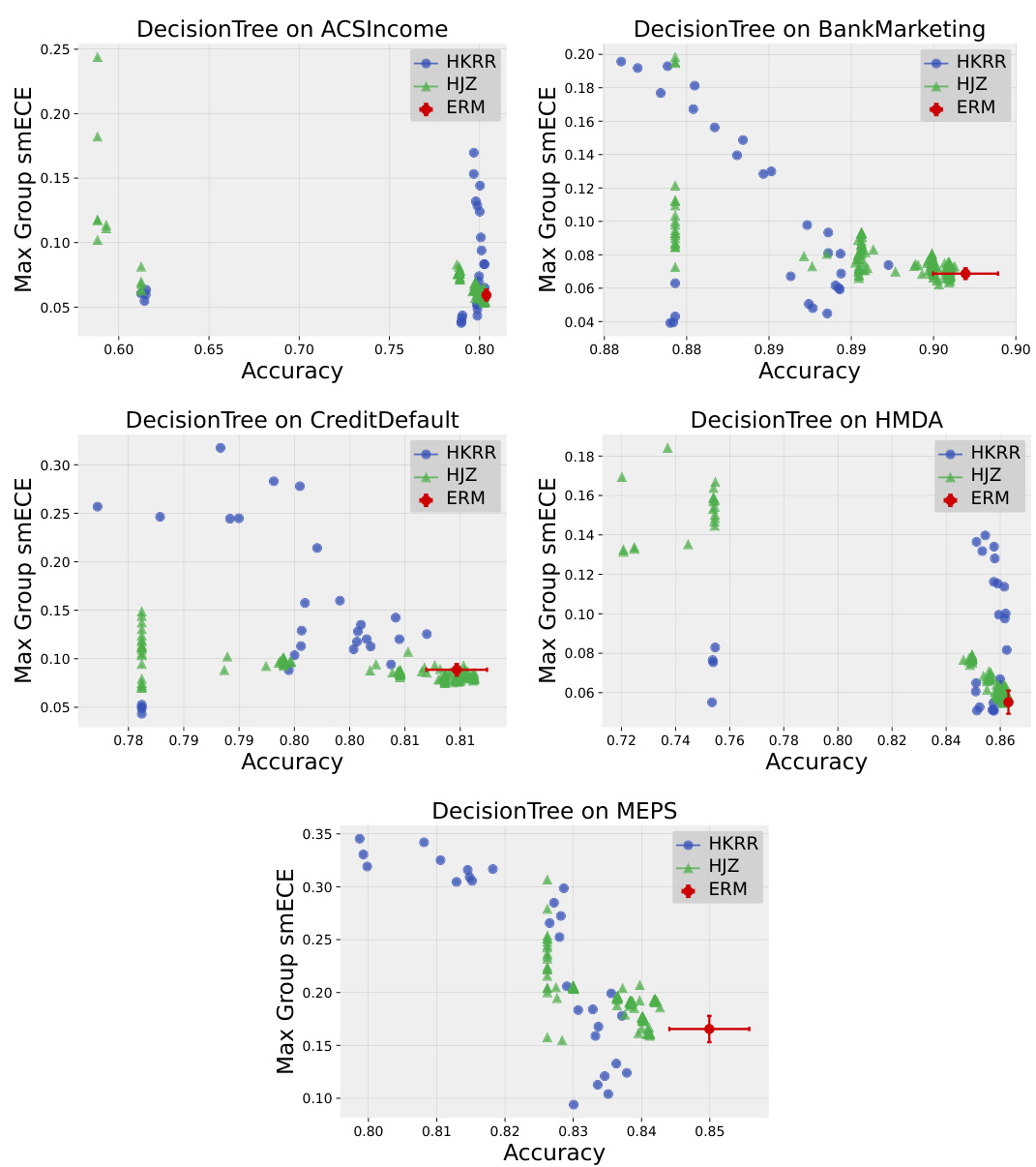
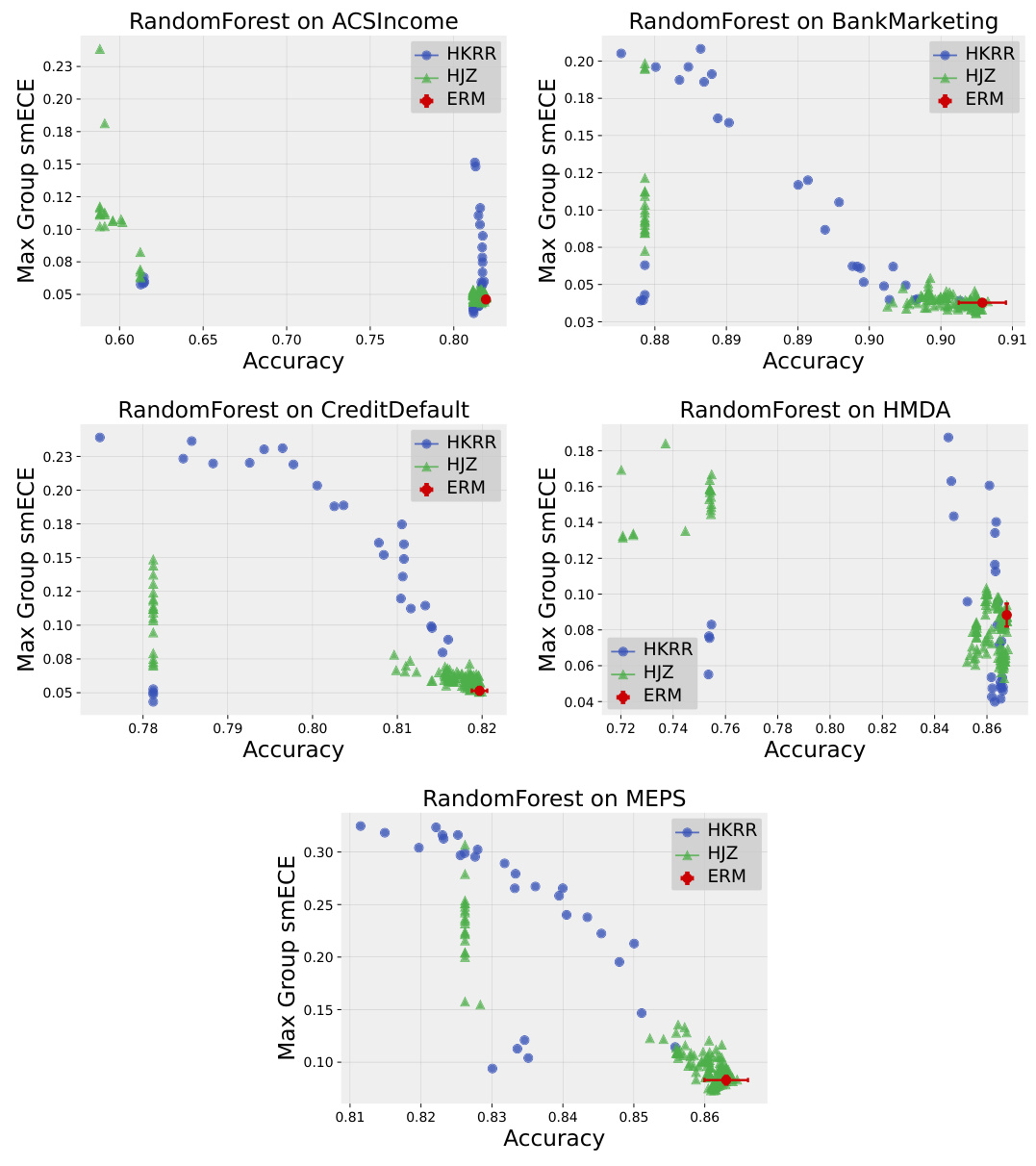
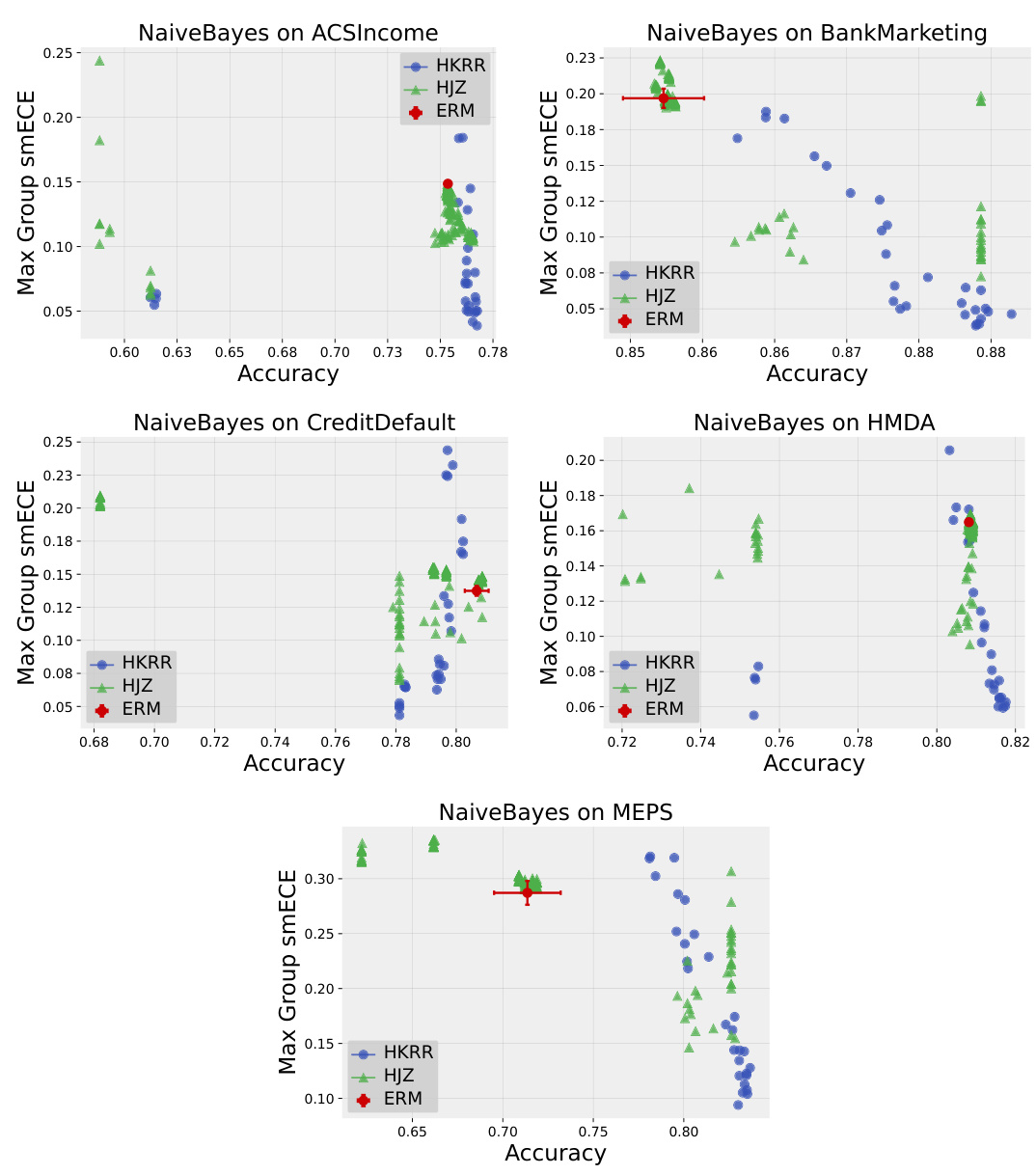
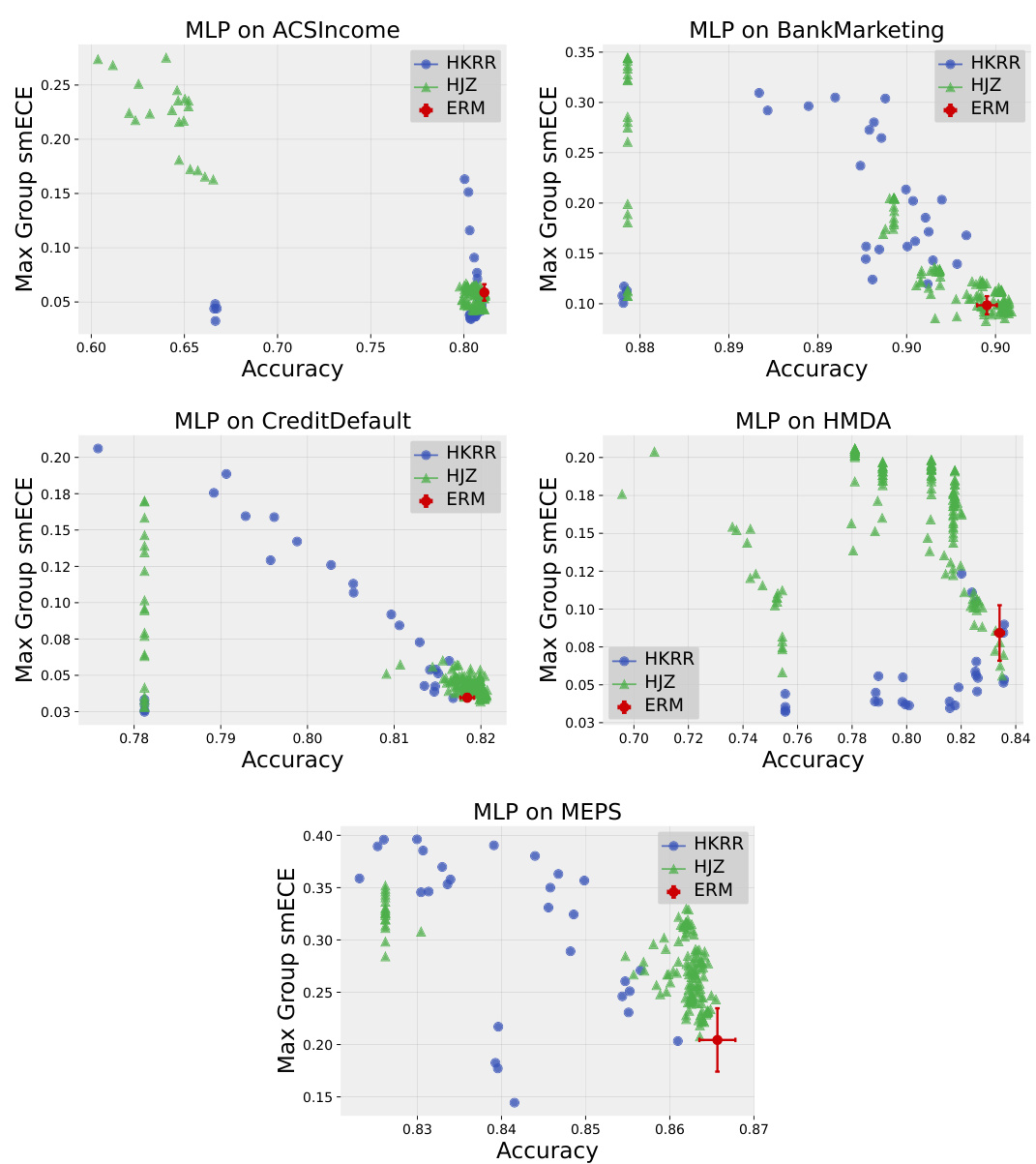
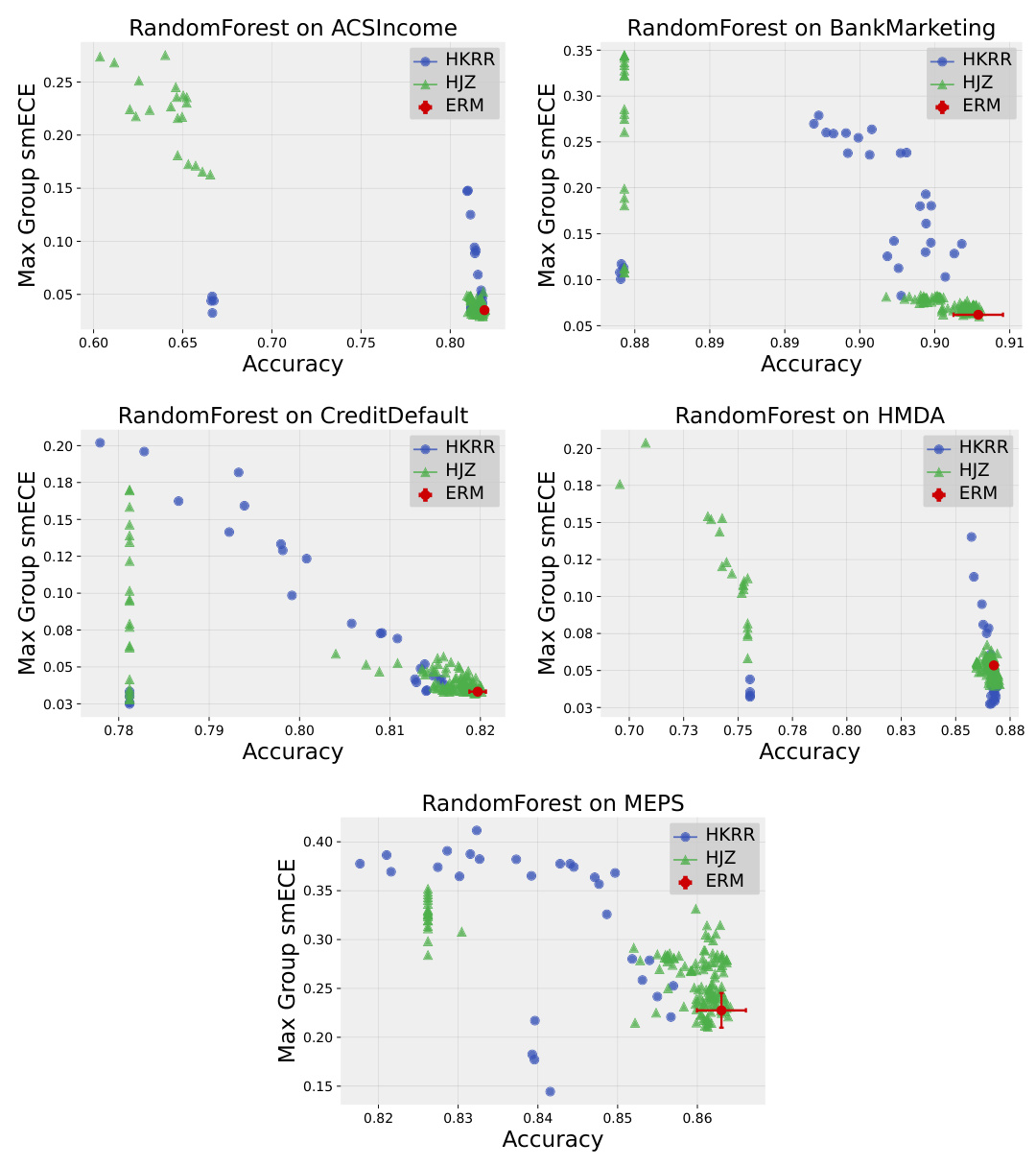
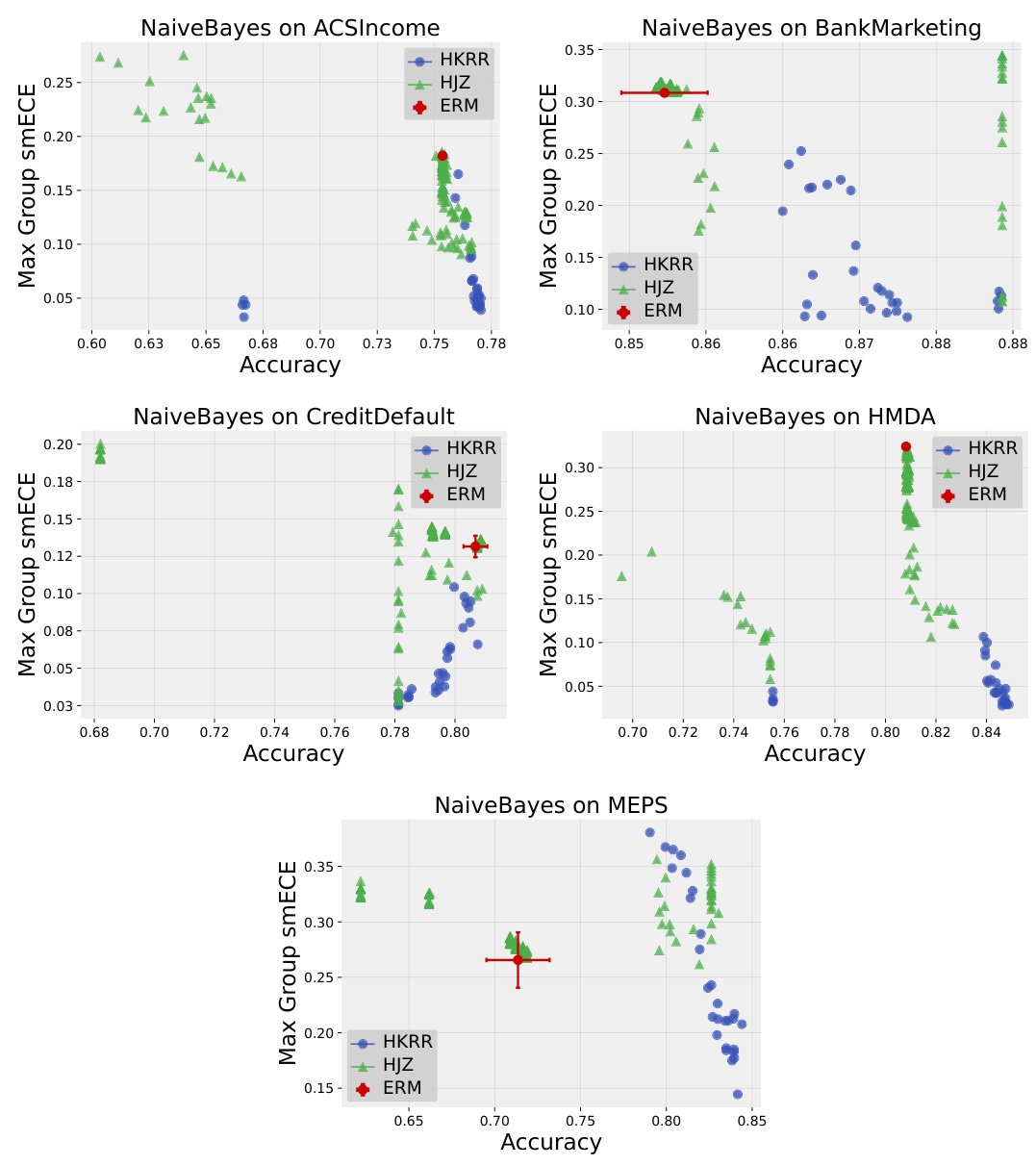
🔼 This figure compares the test accuracy and maximum group-wise calibration error (smECE) of simple Multilayer Perceptrons (MLPs) trained on three different datasets (Credit Default, MEPS, and ACS Income). The comparison is made between standard Empirical Risk Minimization (ERM) and two multicalibration post-processing methods: HKRR and HJZ. Each point represents a model with different hyperparameter settings, showcasing the impact of hyperparameter tuning on the accuracy and calibration of the post-processing algorithms. The figure suggests that ERM training often provides optimal accuracy and calibration without needing post-processing.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.
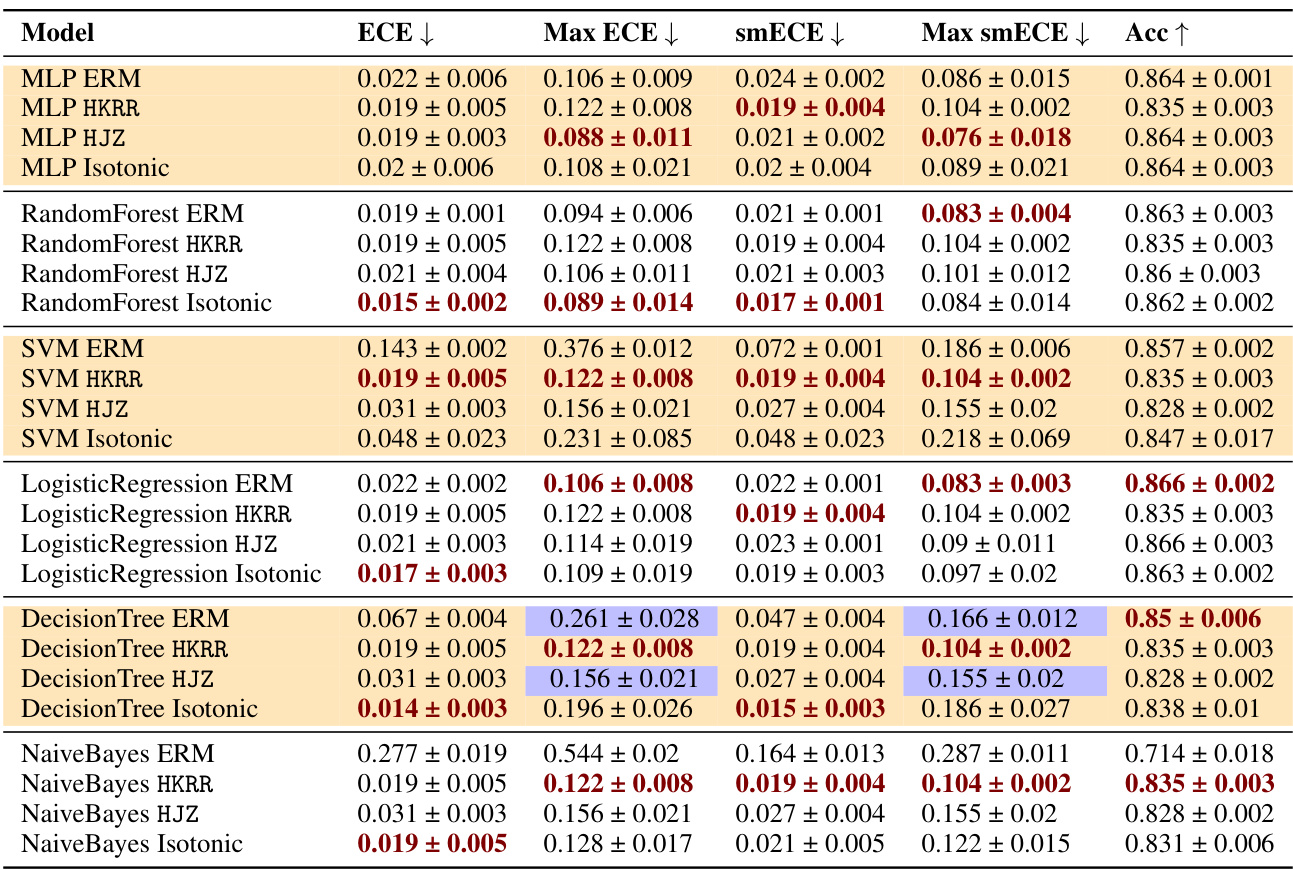
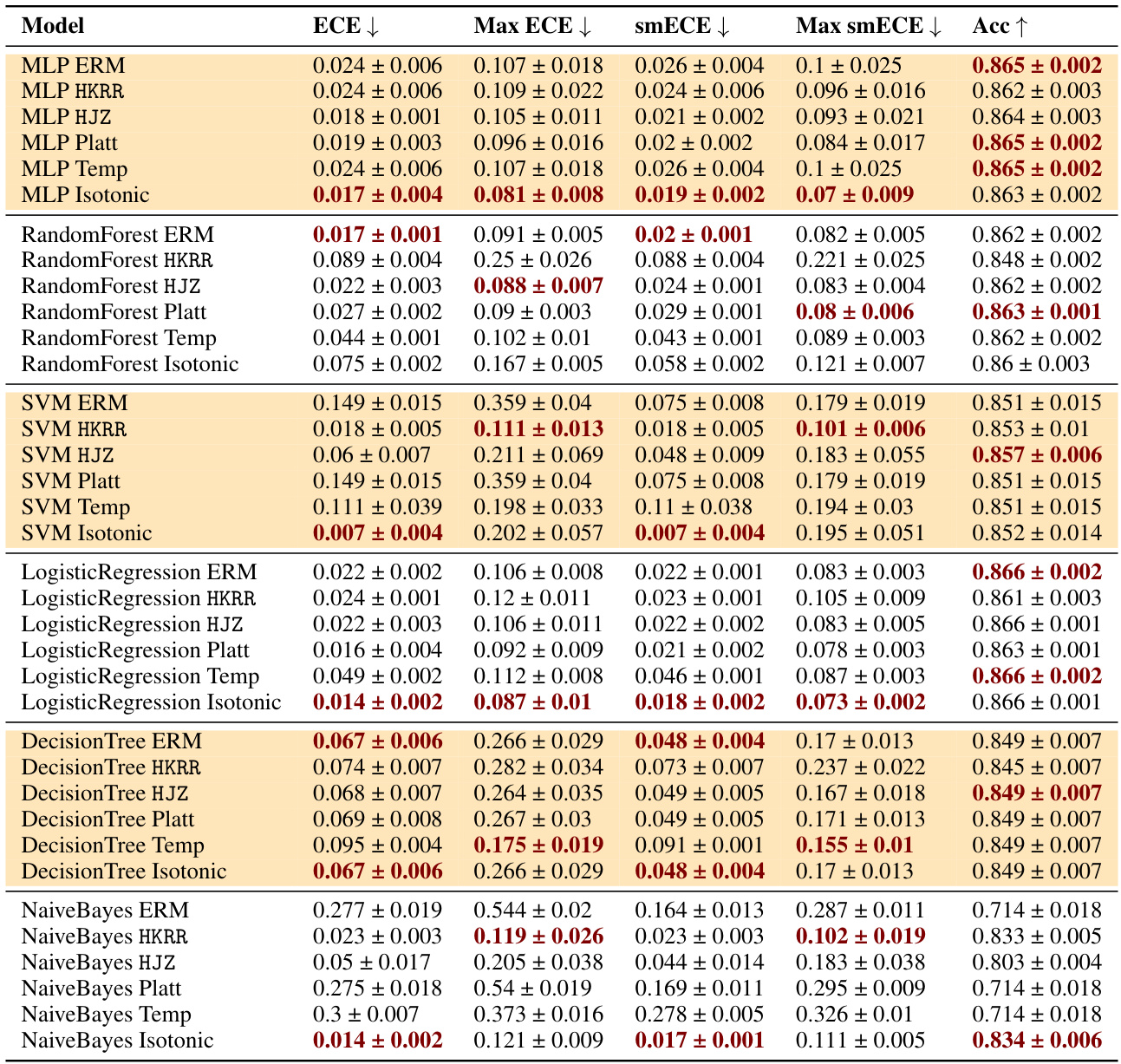
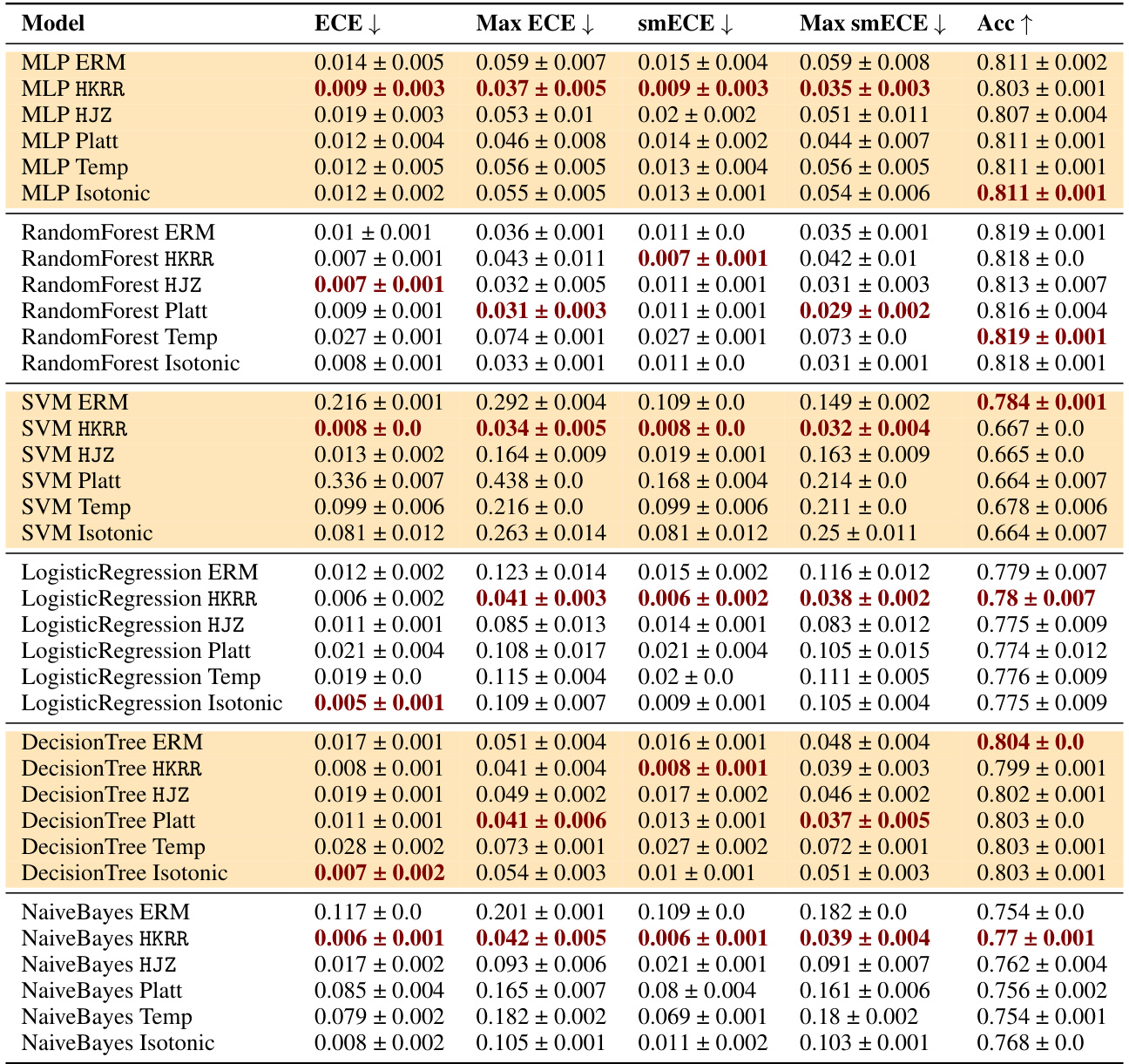
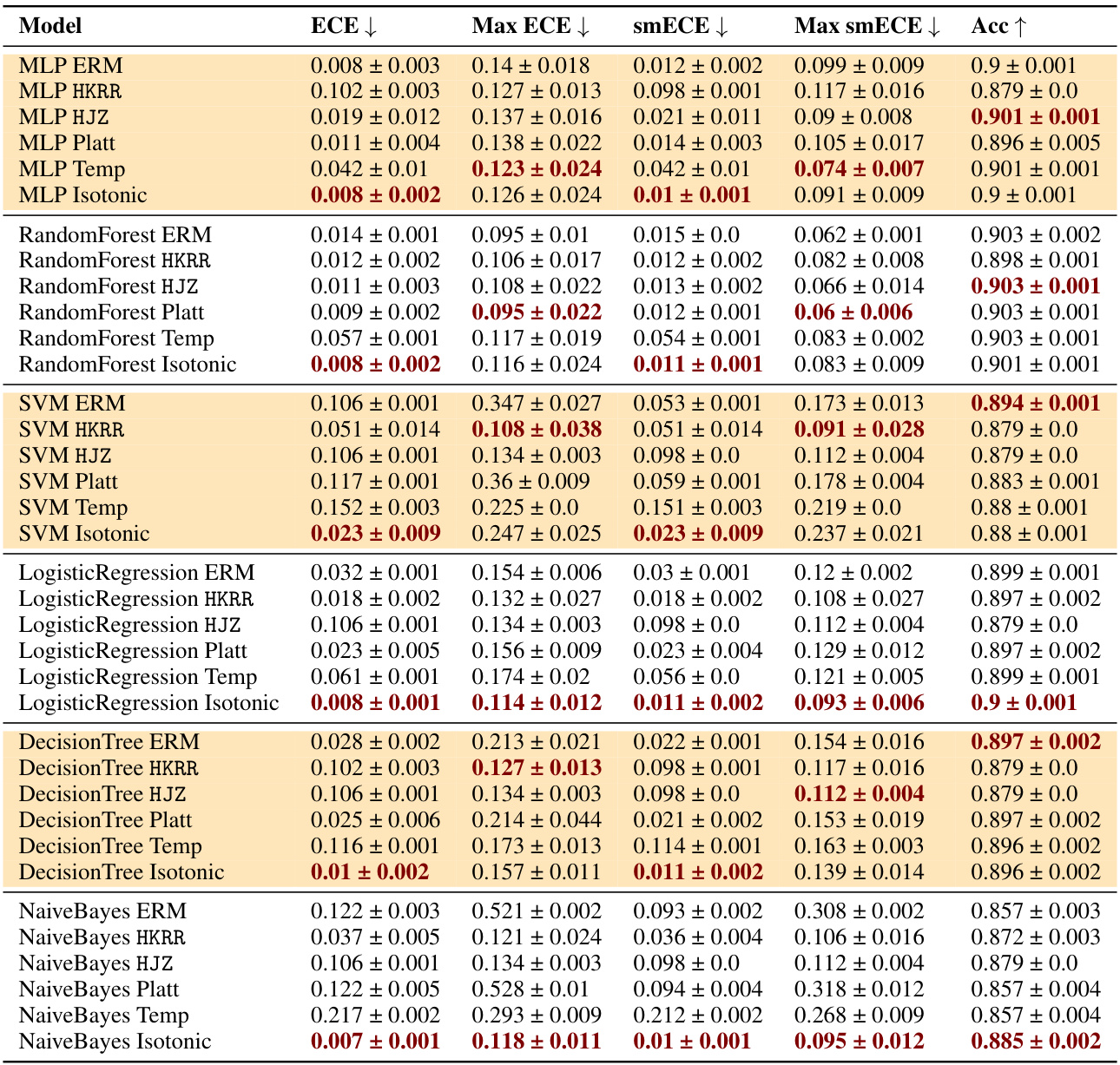
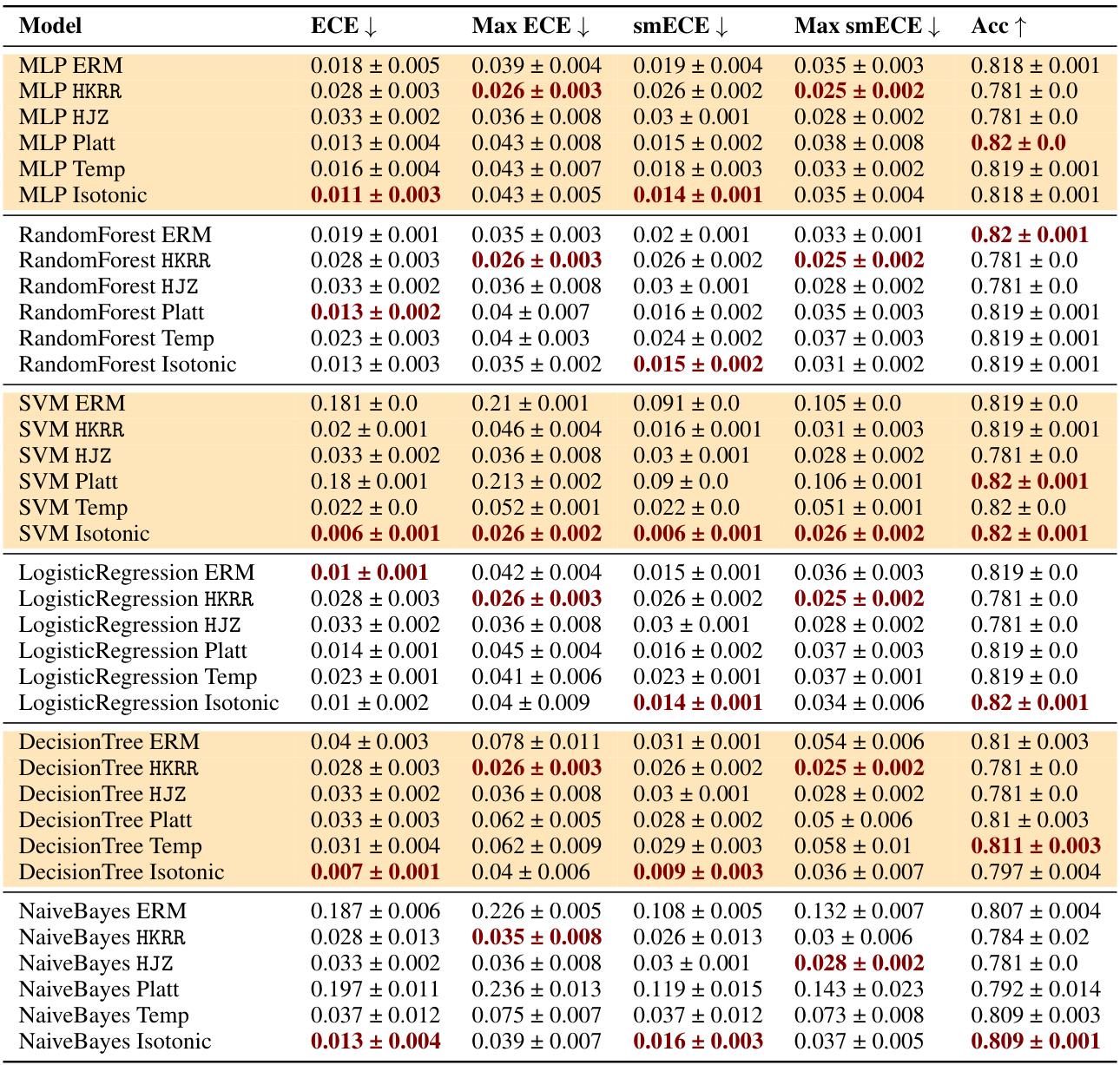
🔼 This table compares the performance of three families of methods for multicalibration: standard ERM, ERM followed by classical recalibration, and ERM followed by explicit multicalibration. It shows the results using different metrics (ECE, max ECE, smECE, max smECE) and accuracy for several machine learning models on the MEPS dataset. The key finding is that well-calibrated models (like MLP, random forests, and logistic regression) often don’t need additional multicalibration post-processing, while uncalibrated models (like SVM, decision trees, and Naive Bayes) benefit from it. The choice of metric (ECE vs smECE) also affects the choice of best method.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.
In-depth insights#
Multicalibration’s Use#
Multicalibration, an extension of standard calibration, is crucial for ensuring fairness and reliability in machine learning models, especially when dealing with sensitive attributes or subgroups. Its primary use lies in mitigating discrimination by guaranteeing calibration across multiple overlapping subpopulations. This is especially important in high-stakes applications like loan applications, healthcare, or criminal justice, where biased predictions can lead to unfair or discriminatory outcomes. The effectiveness of multicalibration depends on several factors, including the quality of the base model, hyperparameter tuning, and data availability. While simply using empirical risk minimization (ERM) can sometimes implicitly yield multicalibrated models, in many cases post-processing algorithms are necessary. However, it is important to note that the trade-off between accuracy and worst-group calibration error needs to be considered when applying these algorithms, particularly for large-scale applications. Further research into the computational efficiency of multicalibration methods and their sensitivity to hyperparameters is needed to facilitate their wider adoption and ensure their effective implementation in real-world applications.
Empirical Study#
An empirical study in a research paper provides concrete evidence to support or refute the claims made. It involves the collection and analysis of real-world data to test hypotheses or explore research questions. A well-conducted empirical study offers stronger validity than purely theoretical approaches, as it directly addresses practical applications and limitations. The data analysis methods employed should be rigorously justified, and the findings must be clearly presented alongside their statistical significance, using appropriate visualizations. The quality and scope of the data, alongside the methodological rigor of the study, greatly influence the credibility and impact of the empirical findings. Detailed descriptions of the data collection process, sample size, and any limitations are crucial to ensure transparency and reproducibility. An effective empirical study offers valuable insights, driving further investigation and potentially informing policy or practice.
Algorithm Effects#
An analysis of algorithm effects in a machine learning context necessitates a multifaceted perspective. Algorithmic bias, stemming from skewed training data, can lead to unfair or discriminatory outcomes, impacting specific demographic groups disproportionately. The choice of algorithm itself introduces variability; different algorithms possess varying sensitivities to biases and differing capacities to generalize across diverse datasets. Model calibration and multicalibration techniques offer potential mitigations, but their effectiveness depends heavily on dataset characteristics and hyperparameter tuning. Post-processing techniques, like recalibration methods, may enhance calibration and multicalibration but do not invariably guarantee fairness. Therefore, a thorough investigation must consider the interplay between data quality, algorithm selection, and post-processing choices to assess the overall effectiveness and equity of the machine learning system.
Practical Guidance#
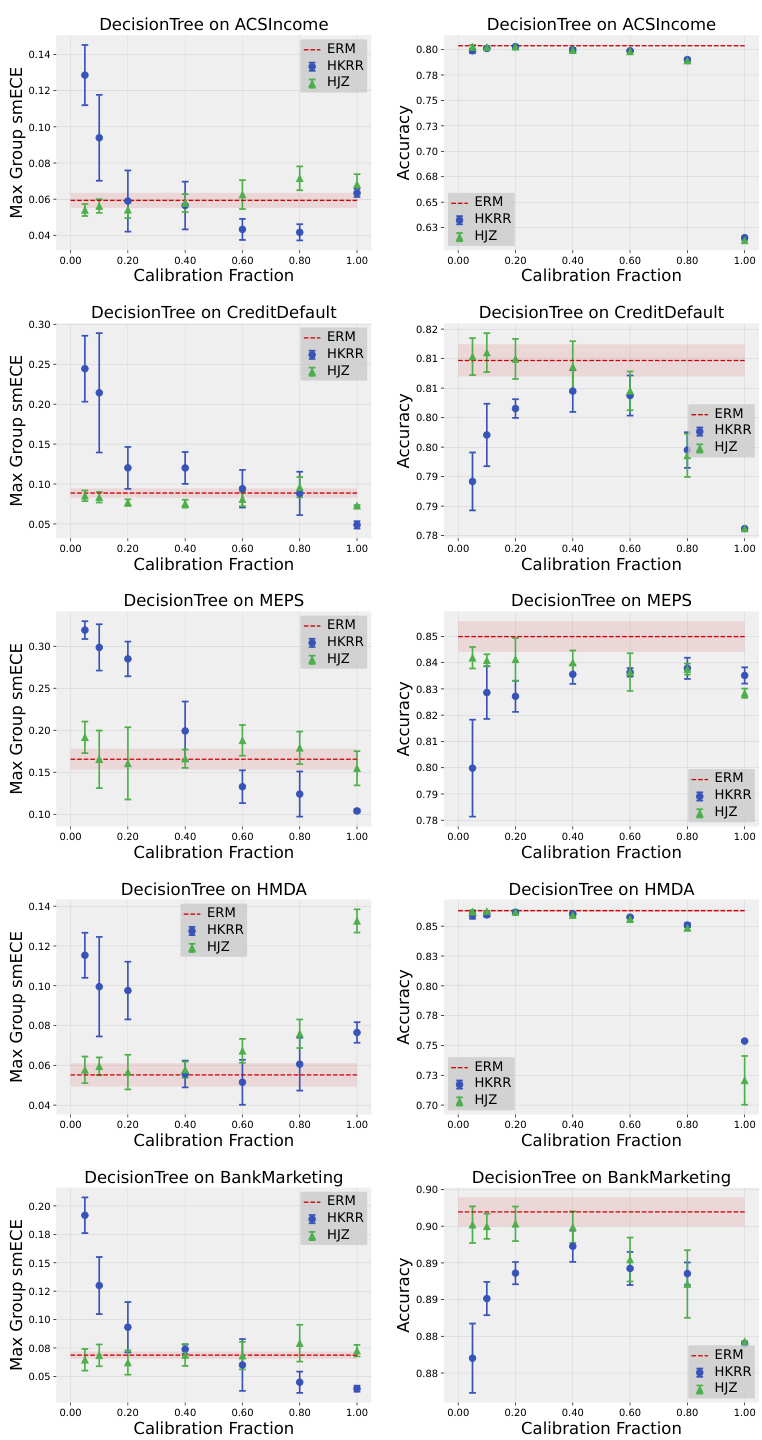
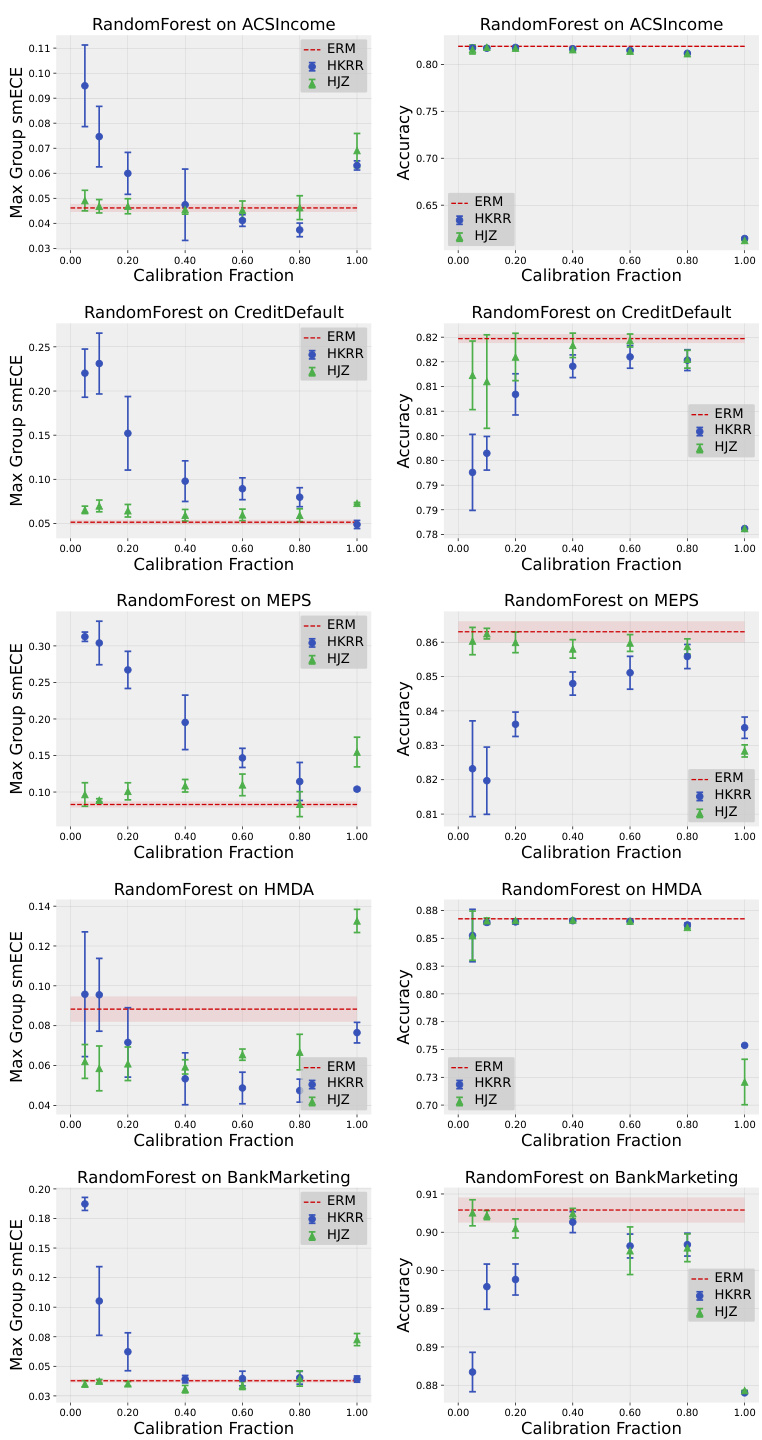
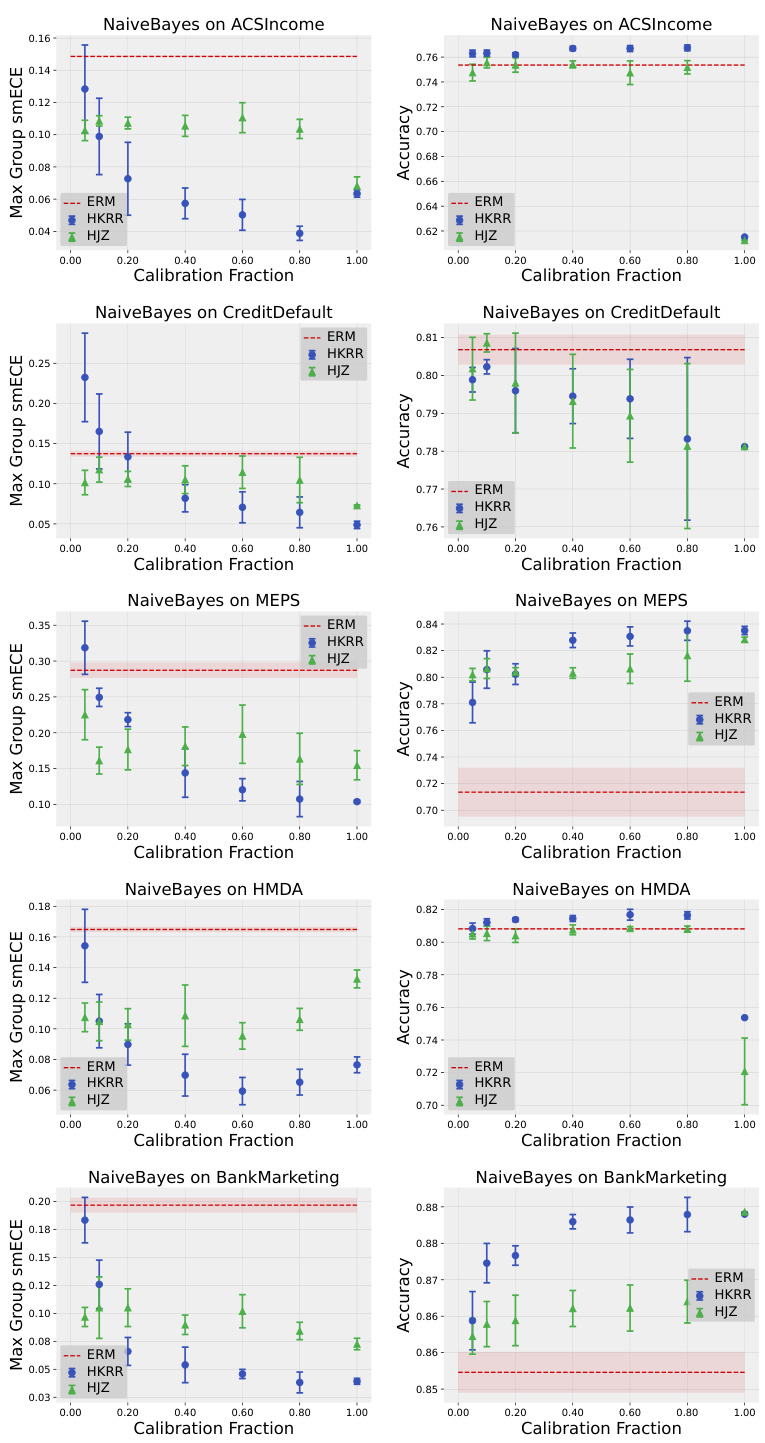
Practical guidance derived from the research emphasizes the subtlety of multicalibration’s impact. While theoretically beneficial, the study reveals that many models, especially those already well-calibrated, demonstrate inherent multicalibration without additional post-processing. Traditional calibration methods often achieve comparable results, highlighting their computational efficiency. The research also underscores the sensitivity of multicalibration algorithms to hyperparameter choices, advocating for extensive parameter sweeps, which may be impractical for real-world applications. Therefore, judicious application of multicalibration post-processing, rather than indiscriminate use, is essential. The trade-off between accuracy and calibration error, particularly at high calibration fractions, further necessitates careful consideration of the cost-benefit tradeoff for different use-cases. Choosing appropriate calibration metrics and understanding their limitations in various dataset settings is another key takeaway for practitioners. Ultimately, the findings stress the importance of empirically evaluating the need for multicalibration in practice before deploying specific algorithms.
Future Research#
Future research directions stemming from this work could involve extending the empirical study to multi-class classification problems and exploring the impact of varying group definitions on multicalibration performance. Investigating the interaction between model calibration and multicalibration, particularly how well-calibrated models behave with respect to multicalibration, is crucial. Developing novel multicalibration algorithms with improved sample efficiency and computational cost is a key area of focus, especially for large datasets and models. Furthermore, research could concentrate on the development of parameter-free multicalibration methods to enhance practicality and usability. Finally, understanding the interplay between multicalibration and various fairness metrics, as well as exploring the potential for theoretical guarantees of multicalibration within the ERM framework for practical applications warrant future consideration.
More visual insights#
More on figures
🔼 This figure compares the test accuracy and maximum group-wise calibration error (smECE) of three different methods for training simple neural networks (MLPs) on three datasets. The methods include standard empirical risk minimization (ERM), ERM followed by the HKRR multicalibration algorithm, and ERM followed by the HJZ multicalibration algorithm. Each point represents a different hyperparameter setting for either HKRR or HJZ. The figure demonstrates that ERM often achieves nearly optimal accuracy and multicalibration error for MLPs.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.

🔼 This figure compares the test accuracy and maximum group-wise calibration error (smECE) of three different approaches for training MLPs on three datasets: standard empirical risk minimization (ERM), ERM followed by the HKRR multicalibration algorithm, and ERM followed by the HJZ multicalibration algorithm. Each point represents a different hyperparameter setting for HKRR or HJZ. The figure shows that ERM often achieves nearly optimal accuracy and multicalibration error, suggesting that explicit multicalibration post-processing may not always be necessary for well-calibrated models.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.

🔼 This figure compares the test accuracy and maximum group-wise calibration error (smECE) of simple neural networks (MLPs) trained using standard empirical risk minimization (ERM) and two multicalibration post-processing methods (HKRR and HJZ) across three datasets. Each point represents a different hyperparameter setting for the post-processing algorithms. The figure shows that ERM often achieves near-optimal accuracy and multicalibration error, suggesting multicalibration post-processing may not always be necessary.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.
🔼 This figure compares the test accuracy and maximum group-wise calibration error (smECE) of three different methods: ERM, HKRR, and HJZ. It demonstrates that on these datasets, standard ERM achieves nearly optimal accuracy and multicalibration error for MLPs. This suggests that additional multicalibration post-processing may not be as beneficial as initially expected.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.
🔼 This figure shows the test accuracy against the maximum group-wise calibration error for three different datasets. Each point represents a different hyperparameter setting for either HKRR or HJZ multicalibration post-processing algorithms. The results indicate that standard empirical risk minimization (ERM) often achieves near optimal accuracy and multicalibration error.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.

🔼 This figure compares the test accuracy and maximum group-wise calibration error (smECE) of three methods: standard empirical risk minimization (ERM), ERM followed by the HKRR algorithm, and ERM followed by the HJZ algorithm. The comparison is performed on three datasets (Credit Default, MEPS, and ACS Income) using simple neural networks. Each point in the scatter plots represents a different hyperparameter setting for the post-processing algorithms. The results show that ERM tends to achieve nearly optimal accuracy and calibration error, suggesting that in some cases, additional post-processing might not be needed. Appendix H includes similar plots for all datasets.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.

🔼 This figure displays the test accuracy versus the maximum group-wise calibration error (smECE) for simple neural networks trained on three different datasets. Each data point represents the performance of either the HKRR or HJZ multicalibration post-processing algorithm with varying hyperparameters. The results show that standard empirical risk minimization (ERM) achieves near optimal accuracy and multicalibration error for MLPs in this scenario.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.
🔼 This figure compares the test accuracy and maximum group-wise calibration error (smECE) for MLPs trained on three different datasets (Credit Default, MEPS, and ACS Income). Each point represents a different hyperparameter setting for either HKRR or HJZ multicalibration post-processing algorithms. The plot shows that standard empirical risk minimization (ERM) often achieves near-optimal results in both accuracy and multicalibration error, suggesting that additional post-processing might not always be necessary. More detailed plots for each dataset are available in the appendix.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.

🔼 This figure compares the test accuracy and maximum group-wise calibration error (smECE) of simple neural networks (MLPs) trained using three different methods: standard empirical risk minimization (ERM), ERM followed by the HKRR multicalibration algorithm, and ERM followed by the HJZ multicalibration algorithm. The results are averaged over five train/validation splits for three datasets: Credit Default, MEPS, and ACS Income. Each point represents a different hyperparameter setting for HKRR or HJZ. The figure shows that ERM achieves near-optimal accuracy and multicalibration error, suggesting that additional multicalibration post-processing may not always be necessary. Additional plots for each dataset are found in Appendix H.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.
🔼 This figure shows the test accuracy and maximum group-wise calibration error for three datasets (Credit Default, MEPS, and ACS Income). Three multicalibration post-processing algorithms (HKRR, HJZ) are compared against standard Empirical Risk Minimization (ERM). Each point represents a different hyperparameter setting for the post-processing algorithms. The results demonstrate that ERM often achieves accuracy and multicalibration error close to optimal for simple neural networks.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.
🔼 This figure displays the test accuracy against the maximum group-wise calibration error for simple neural networks trained on three different datasets: Credit Default, MEPS, and ACS Income. Each point represents a different hyperparameter setting for either the HKRR or HJZ multicalibration post-processing algorithms. The figure demonstrates that standard empirical risk minimization (ERM) often achieves nearly optimal accuracy and multicalibration error, suggesting multicalibration post-processing may not always be necessary for well-calibrated models.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.

🔼 This figure displays the results of a comparison between three methods for achieving multicalibration in simple neural networks on three different datasets. The x-axis represents the test accuracy, and the y-axis represents the maximum group-wise calibration error (smECE). Each point represents a different hyperparameter setting for either the HKRR or HJZ multicalibration algorithms. The figure shows that standard empirical risk minimization (ERM) often achieves nearly optimal accuracy and multicalibration without additional post-processing, suggesting that for well-calibrated models, additional multicalibration steps may not be necessary. Additional plots for each dataset are included in Appendix H of the paper.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.

🔼 This figure compares the test accuracy and maximum group-wise calibration error (smECE) of simple neural networks (MLPs) trained using three different methods: standard empirical risk minimization (ERM), ERM followed by HKRR, and ERM followed by HJZ. Each point represents a different hyperparameter setting for the post-processing algorithms (HKRR or HJZ). The results show that ERM achieves nearly optimal accuracy and multicalibration error, indicating that additional post-processing may not always be necessary.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.
🔼 This figure shows the test accuracy plotted against the maximum group-wise calibration error (smECE) for Multilayer Perceptrons (MLPs) trained on three different datasets (Credit Default, MEPS, and ACS Income). Each data point represents a different hyperparameter configuration for either the HKRR or HJZ multicalibration post-processing algorithms. The figure demonstrates that standard Empirical Risk Minimization (ERM) achieves near-optimal results in terms of both accuracy and multicalibration error for these simple models.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.

🔼 This figure compares the test accuracy and maximum group-wise calibration error (smECE) of three different methods for training simple neural networks (MLPs) on three different datasets. The three methods are: standard empirical risk minimization (ERM), ERM followed by the HKRR multicalibration algorithm, and ERM followed by the HJZ multicalibration algorithm. Each point on the plot represents the performance of one of the multicalibration algorithms with a specific hyperparameter setting. The figure shows that ERM often achieves accuracy and multicalibration error close to optimal.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.

🔼 This figure compares the performance of different multicalibration post-processing algorithms (HKRR and HJZ) against standard empirical risk minimization (ERM) for simple neural networks (MLPs) trained on three different datasets. The x-axis represents test accuracy, while the y-axis shows the maximum group-wise calibration error (smECE), which measures the worst-case calibration error among different subgroups. Each point on the plot represents a different configuration of the post-processing algorithm’s hyperparameters. The figure demonstrates that ERM often achieves near-optimal accuracy and multicalibration error, indicating that additional post-processing might not always be necessary.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.

🔼 This figure compares the test accuracy and maximum group-wise calibration error (smECE) of three different methods for training simple neural networks (MLPs) on three datasets: Credit Default, MEPS, and ACS Income. The three methods are standard empirical risk minimization (ERM), ERM followed by HKRR, and ERM followed by HJZ. Each point in the plot represents the performance of a single model trained with a particular set of hyperparameters. The x-axis represents test accuracy, and the y-axis represents the maximum group-wise calibration error, which measures how well the model is calibrated across different subgroups. The figure shows that standard ERM achieves nearly optimal accuracy and multicalibration error for MLPs, indicating that additional post-processing may not always be necessary to achieve good multicalibration.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.
🔼 This figure displays the trade-off between test accuracy and maximum group-wise calibration error (smECE) for Multilayer Perceptrons (MLPs) trained on three datasets: Credit Default, MEPS, and ACS Income. The x-axis represents the test accuracy, and the y-axis represents the maximum group-wise smECE. Each point in the scatter plot corresponds to a run of either the HKRR or HJZ multicalibration post-processing algorithm with a specific set of hyperparameters. The plot shows that standard empirical risk minimization (ERM) achieves nearly optimal accuracy and multicalibration error for MLPs, suggesting that additional multicalibration post-processing is often unnecessary. Similar plots for other datasets are provided in Appendix H.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.
🔼 This figure compares the test accuracy and maximum group-wise calibration error for simple neural networks trained on three datasets using three different methods: standard empirical risk minimization (ERM), ERM followed by HKRR, and ERM followed by HJZ. Each point represents a different hyperparameter setting for the post-processing algorithms. The figure shows that ERM alone achieves near optimal accuracy and calibration error in most cases.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.
🔼 This figure compares the test accuracy and maximum group-wise calibration error (smECE) of simple neural networks (MLPs) trained using standard empirical risk minimization (ERM) and two multicalibration post-processing algorithms (HKRR and HJZ) across three datasets (Credit Default, MEPS, and ACS Income). Each point represents a model trained with different hyperparameters. The figure shows that ERM achieves near-optimal accuracy and calibration error in most cases. Appendix H contains similar plots for all datasets.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.
🔼 This figure compares the test accuracy and maximum group-wise calibration error (smECE) for different hyperparameter settings of multicalibration post-processing algorithms (HKRR and HJZ) and standard empirical risk minimization (ERM) on three datasets: Credit Default, MEPS, and ACS Income. Each data point represents the results from one train-validation split. The results show that ERM achieves near-optimal accuracy and multicalibration error, suggesting multicalibration may not always be necessary.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.
🔼 This figure shows the test accuracy and maximum group-wise calibration error for simple neural networks trained on three datasets. Each point represents a model trained with empirical risk minimization (ERM) and then post-processed with either the HKRR or HJZ multicalibration algorithm, using different hyperparameter settings. It demonstrates that ERM alone often achieves near-optimal accuracy and multicalibration. Appendix H contains similar plots for other datasets.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.

🔼 This figure compares the test accuracy and maximum group-wise calibration error for simple neural networks trained on three datasets using standard empirical risk minimization (ERM) and two multicalibration post-processing algorithms (HKRR and HJZ). Each point represents a different hyperparameter setting for the post-processing algorithms. The results show that ERM often achieves nearly optimal accuracy and multicalibration, suggesting that additional post-processing may not always be necessary.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.

🔼 This figure compares the test accuracy and maximum group-wise calibration error (smECE) of simple neural networks (MLPs) trained using three different methods: standard empirical risk minimization (ERM), ERM followed by HKRR post-processing, and ERM followed by HJZ post-processing. Each point represents a model trained with a specific set of hyperparameters for the chosen post-processing method. The plots show that ERM often achieves near-optimal accuracy and calibration error, indicating that additional post-processing may not always be necessary.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.
🔼 This figure displays the results of a large-scale evaluation comparing three families of methods for multicalibration: standard ERM, ERM followed by recalibration, and ERM followed by explicit multicalibration. The x-axis represents test accuracy, and the y-axis represents the maximum group-wise calibration error (smECE) averaged across five train/validation splits for each algorithm and hyperparameter set. The plot demonstrates that ERM performs nearly optimally in terms of both accuracy and multicalibration error for simple neural networks (MLPs).
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.

🔼 This figure shows the test accuracy against the maximum group-wise calibration error for simple neural networks trained on three different datasets. Each data point represents the performance of either the HKRR or HJZ multicalibration post-processing algorithms using various hyperparameter settings. The results demonstrate that standard empirical risk minimization (ERM) often achieves nearly optimal accuracy and multicalibration error without requiring additional post-processing.
read the caption
Figure 1: Test accuracy vs. maximum group-wise calibration error (smECE) averaged over five train/validation splits for simple neural networks (MLPs) trained on Credit Default, MEPS, and ACS Income. Each point corresponds to the performance of the multicalibration post-processing algorithm HKRR (Hébert-Johnson et al., 2018) or HJZ (Haghtalab et al., 2023) with a different choice of hyperparameters. Standard empirical risk minimization (ERM) for MLPs achieves nearly optimal accuracy and multicalibration error. Similar plots for each dataset are in Appendix H.
More on tables

🔼 This table compares the performance of different multicalibration post-processing algorithms (HKRR, HJZ, Platt scaling, isotonic regression) against a standard ERM baseline on the MEPS dataset. It shows the ECE, max ECE, smECE, max smECE, and accuracy for various models (MLP, Random Forest, Logistic Regression, SVM, Decision Tree, Naive Bayes). The results highlight that well-calibrated models don’t significantly benefit from post-processing, while poorly calibrated models show improvements when applying multicalibration algorithms. The choice of evaluation metric (ECE vs smECE) impacts results.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.
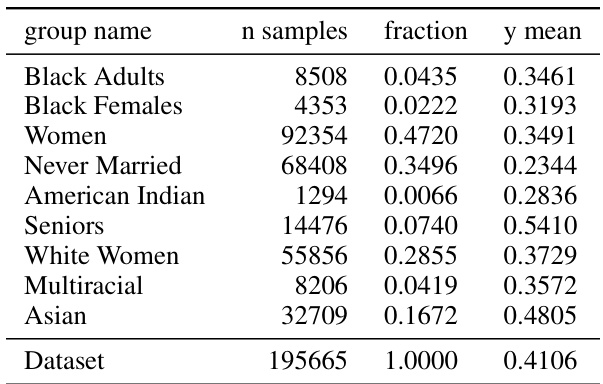
🔼 This table shows the different subgroups used in the ACS Income dataset experiments. For each subgroup, it provides the number of samples, the fraction of the total dataset represented by that subgroup, and the mean of the target variable (y) within that subgroup. The groups are defined by sensitive attributes such as race, marital status, and age to assess fairness and multicalibration in the model’s predictions.
read the caption
Figure 6: ACS Income groups.

🔼 This table presents the subgroups used in the Bank Marketing dataset experiments. Each row shows a subgroup name, the number of samples in that subgroup, the fraction of the total dataset represented by that subgroup, and the mean of the target variable (y) within that subgroup. The ‘Dataset’ row provides the total number of samples and the overall mean of the target variable.
read the caption
Figure 7: Bank Marketing groups.

🔼 This table shows the subgroups used in the multicalibration experiments on the Credit Default dataset. Each row represents a subgroup defined by one or more features (e.g., gender, age, marital status, education level). The table shows the number of samples in each subgroup, the fraction of the total dataset represented by the subgroup, and the mean of the outcome variable (y) for the subgroup.
read the caption
Figure 8: Credit Default groups.
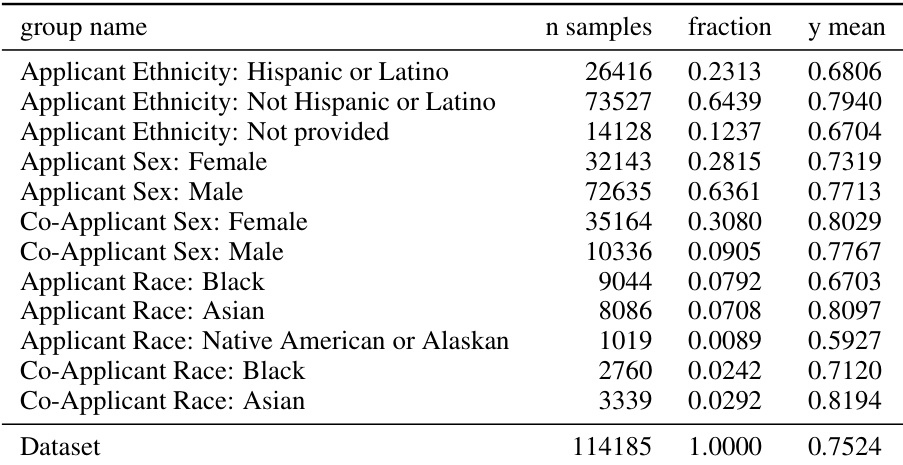
🔼 This table presents the subgroups considered for the HMDA dataset in the experiments. The table shows the group name, the number of samples in each group, the fraction of the entire dataset that each group represents, and the mean of the y-variable for each group. Note that the ‘Dataset’ row does not represent a group used in multicalibration post-processing; those aggregate metrics are not used to compute worst-group metrics.
read the caption
Figure 9: HMDA groups.
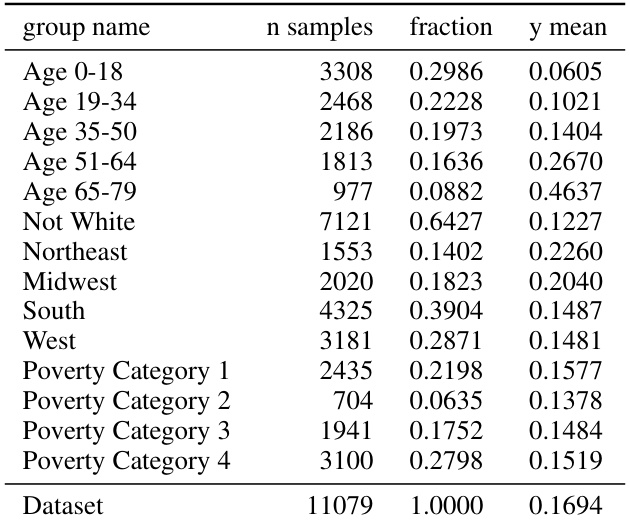
🔼 This table shows the subgroups used in the MEPS dataset for multicalibration experiments. These subgroups are defined by demographic features (age, race) and socioeconomic characteristics (poverty category, location). The table lists each subgroup’s name, number of samples, the fraction of the total dataset it represents, and the mean outcome value (y mean) for that subgroup.
read the caption
Figure 10: MEPS groups.

🔼 This table shows the alternate groups used for the ACS Income dataset in the experiments described in the paper. The groups are defined by one or a combination of features, focusing on demographic characteristics relevant to fairness considerations. The table lists each group’s name, number of samples, fraction of the total dataset, and the mean of the target variable (income) for that group.
read the caption
Figure 11: ACS Income alternate groups.

🔼 This table compares the performance of three families of methods for achieving multicalibration: standard ERM, ERM followed by recalibration, and ERM followed by explicit multicalibration. The results show that ERM alone is often a strong baseline and that multicalibration algorithms do not always improve worst-group calibration error. The choice of calibration metric (ECE vs. smECE) can also impact the choice of the best post-processing method.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.
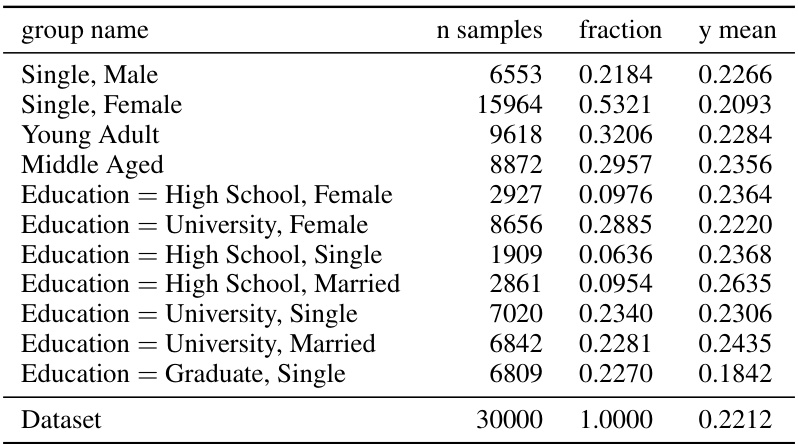
🔼 This table lists the subgroups used in the multicalibration experiments for the Credit Default dataset. Each row represents a subgroup defined by one or more features (e.g., gender, age, marital status, education level). The ’n samples’ column indicates the number of samples in each subgroup, ‘fraction’ shows the proportion of the whole dataset each subgroup represents, and ‘y mean’ shows the average outcome (positive label fraction) for the samples in the subgroup. These subgroups were chosen to represent different segments of the population where fairness concerns might be relevant.
read the caption
Figure 8: Credit Default groups.

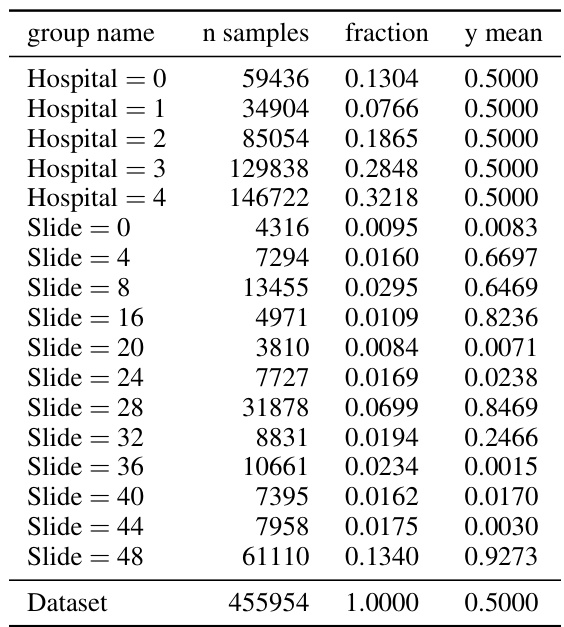
🔼 This table lists the subgroups used in the multicalibration experiments for the HMDA dataset. Each row represents a subgroup defined by one or more features (e.g., Applicant Ethnicity, Applicant Sex, Co-Applicant Sex, Applicant Race, Co-Applicant Race). The table shows the number of samples in each subgroup, the fraction of the total dataset that subgroup represents, and the average value of the dependent variable (y mean) within that subgroup. These subgroups are used to assess the model’s calibration across different demographic segments and help evaluate fairness-related concerns.
read the caption
Figure 9: HMDA groups.

🔼 This table compares the performance of different multicalibration post-processing algorithms (HKRR, HJZ) against standard ERM on the MEPS dataset, across various machine learning models. The results show that calibrated models (like MLP, random forests, logistic regression) do not benefit much from post-processing. Conversely, uncalibrated models (like SVM, decision trees, Naive Bayes) show improvements in max smECE with post-processing. The table also highlights the importance of metric choice (ECE vs smECE) in selecting the optimal algorithm.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.
🔼 This table compares the performance of three families of methods for multicalibration: standard ERM, ERM followed by recalibration, and ERM followed by explicit multicalibration algorithms. The comparison is made using four metrics: ECE, max ECE, smECE, and max smECE. The results show that ERM alone is often a strong baseline, and calibrated models often do not require post-processing. However, uncalibrated models benefit from post-processing. The choice of metric (ECE vs smECE) can affect which method is preferred.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.
🔼 This table compares the performance of three families of methods for multicalibration: standard ERM, ERM followed by recalibration, and ERM followed by explicit multicalibration. It shows that ERM alone is often a strong baseline, and that multicalibration algorithms do not always improve worst group calibration error. The table highlights the sensitivity of multicalibration algorithms to hyperparameter choices and suggests that traditional calibration methods can sometimes provide similar performance.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.
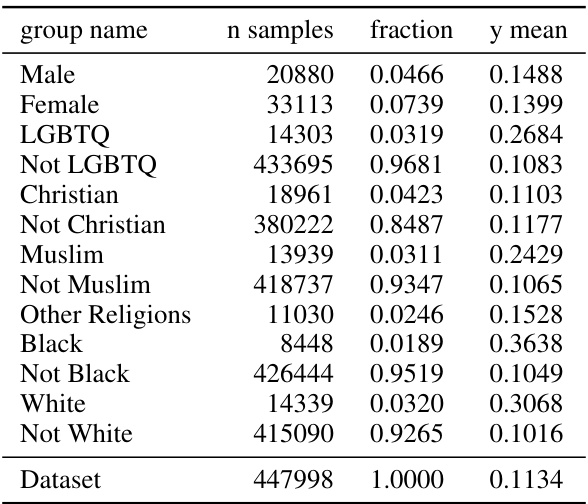
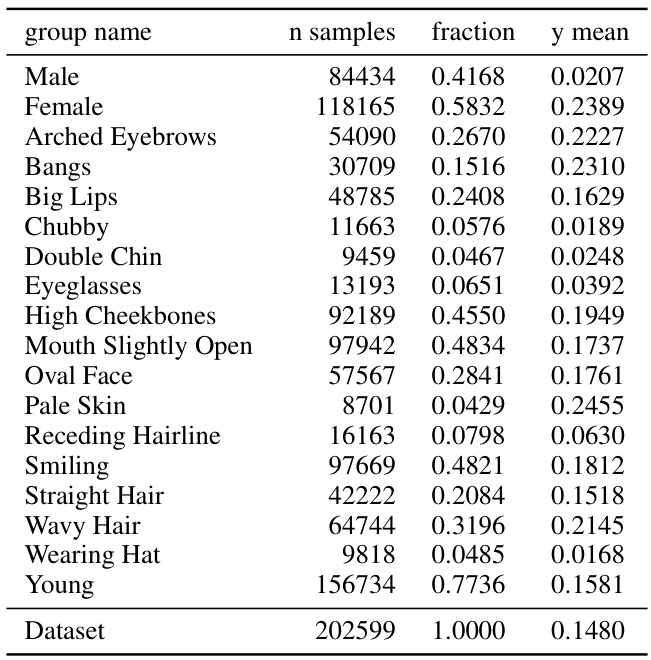
🔼 This table shows the different subgroups used in the Civil Comments dataset. Each row represents a subgroup defined by one or more features (e.g., gender, religious affiliation). The ’n samples’ column indicates the number of samples in each subgroup, ‘fraction’ shows the proportion of the total dataset each subgroup represents, and ‘y mean’ indicates the average of the target variable (toxicity) for each group. The dataset is imbalanced with some groups (like LGBTQ) being heavily overrepresented in positive labels.
read the caption
Figure 18: Civil Comments groups.
🔼 This table compares the performance of three families of methods for multicalibration: standard ERM, ERM followed by recalibration, and ERM followed by explicit multicalibration. It shows the ECE, max ECE, smECE, max smECE and accuracy for several models (MLP, Random Forest, SVM, Logistic Regression, Decision Tree, and Naive Bayes) on the MEPS dataset. The results highlight that calibrated models often don’t need additional multicalibration, while uncalibrated models benefit from post-processing. The choice of evaluation metric (ECE vs. smECE) can also impact the choice of best method.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.

🔼 This table compares the performance of three families of methods on the MEPS dataset: standard ERM, ERM followed by a classical recalibration method, and ERM followed by an explicit multicalibration algorithm. For each method, the table shows the ECE, max ECE, smECE, max smECE, and accuracy. The table highlights the fact that ERM alone is often a strong baseline, and that multicalibration algorithms do not always improve worst-group calibration error. The table also shows the importance of the choice of metric for selecting the best post-processing method. For example, choosing between ECE and smECE for decision trees can result in selecting different models.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.

🔼 This table compares the performance of three multicalibration post-processing algorithms (HKRR, HJZ, and isotonic regression) against the standard ERM baseline on the MEPS dataset. It shows the ECE, Max ECE, smECE, Max smECE, and Accuracy for various models (MLP, Random Forest, Logistic Regression, SVM, Decision Tree, Naive Bayes). The table highlights the subtle differences in the results based on the choice of the calibration metric (ECE vs. smECE). It shows that calibrated models perform similarly to post-processed models. However, uncalibrated models improve with post-processing. The choice of metric for decision trees impact the selection of the best model.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.
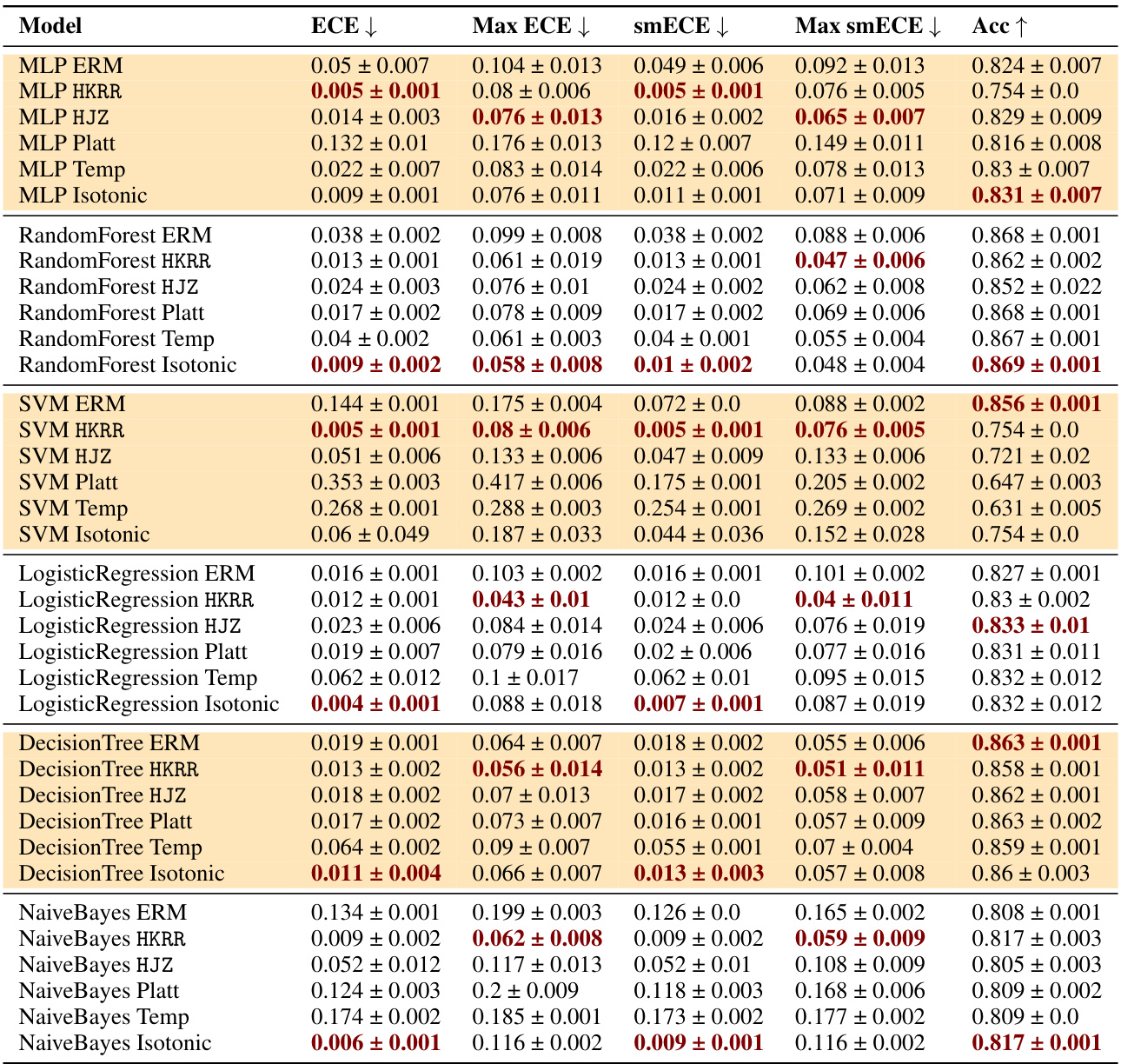
🔼 This table compares the performance of three families of methods for multicalibration: standard ERM, ERM followed by recalibration, and ERM followed by explicit multicalibration algorithms. It shows that ERM alone is a strong baseline for certain models, while multicalibration algorithms sometimes improve error for models that are not well-calibrated initially. The results highlight the importance of choosing the right evaluation metric and the sensitivity of multicalibration algorithms to hyperparameter selection. It’s a detailed performance breakdown for various ML models on MEPS dataset, showing ECE, Max ECE, smECE, Max smECE, and Accuracy metrics across three post-processing algorithm groups and standard ERM.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.

🔼 This table compares the performance of three families of methods for achieving multicalibration: standard ERM, ERM followed by recalibration, and ERM followed by explicit multicalibration. It shows the ECE, maxECE, smECE, max smECE, and accuracy for various models (MLP, Random Forest, SVM, Logistic Regression, Decision Tree, Naive Bayes) on the MEPS dataset. The results highlight that for well-calibrated models, additional multicalibration steps don’t significantly improve the worst-group calibration error. Conversely, for poorly calibrated models, multicalibration algorithms can improve the worst-group calibration error, although the impact may depend on the choice of calibration metric (ECE vs. smECE).
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.

🔼 This table presents a comparison of the performance of three families of methods for achieving multicalibration: standard ERM, ERM followed by classical recalibration, and ERM followed by explicit multicalibration algorithms. The results are shown for various machine learning models (MLP, Random Forest, SVM, Logistic Regression, Decision Tree, Naive Bayes) on the MEPS dataset. The table highlights that calibrated models often do not require additional post-processing for multicalibration, while uncalibrated models benefit from multicalibration post-processing. The choice of metric (ECE vs. smECE) for evaluating multicalibration can influence the selection of the best post-processing method.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.

🔼 This table compares the performance of three families of methods for achieving multicalibration: standard ERM, ERM followed by recalibration, and ERM followed by explicit multicalibration. The results show that ERM alone is often a strong baseline, and multicalibration algorithms do not always improve worst-group calibration error. The table highlights the sensitivity of multicalibration algorithms to hyperparameter choices and the effectiveness of traditional calibration methods.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.

🔼 This table shows the performance comparison of three families of methods for multicalibration: standard ERM, ERM followed by a classical recalibration method, and ERM followed by an explicit multicalibration algorithm. The results are presented as mean ± standard deviation for ECE, Max ECE, smECE, Max smECE, and Accuracy. The best-performing hyperparameters for HKRR and HJZ algorithms are selected based on validation max smECE. The table highlights that calibrated models (MLP, Random Forest, Logistic Regression) do not require post-processing to achieve multicalibration, whereas uncalibrated models (SVM, Decision Tree, Naive Bayes) significantly benefit from multicalibration post-processing. The choice of metric (ECE vs. smECE) is also shown to influence the selection of the best post-processing method for Decision Trees.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.

🔼 This table compares the performance of three families of methods for multicalibration: standard ERM, ERM followed by recalibration, and ERM followed by explicit multicalibration. It shows the ECE, max ECE, smECE, max smECE, and accuracy for different models (MLP, Random Forest, SVM, Logistic Regression, Decision Tree, Naive Bayes) on the MEPS dataset. The results highlight that models which are already well-calibrated often don’t benefit from further multicalibration post-processing and that the choice of calibration metric (ECE vs. smECE) can influence which algorithm is selected as optimal.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.
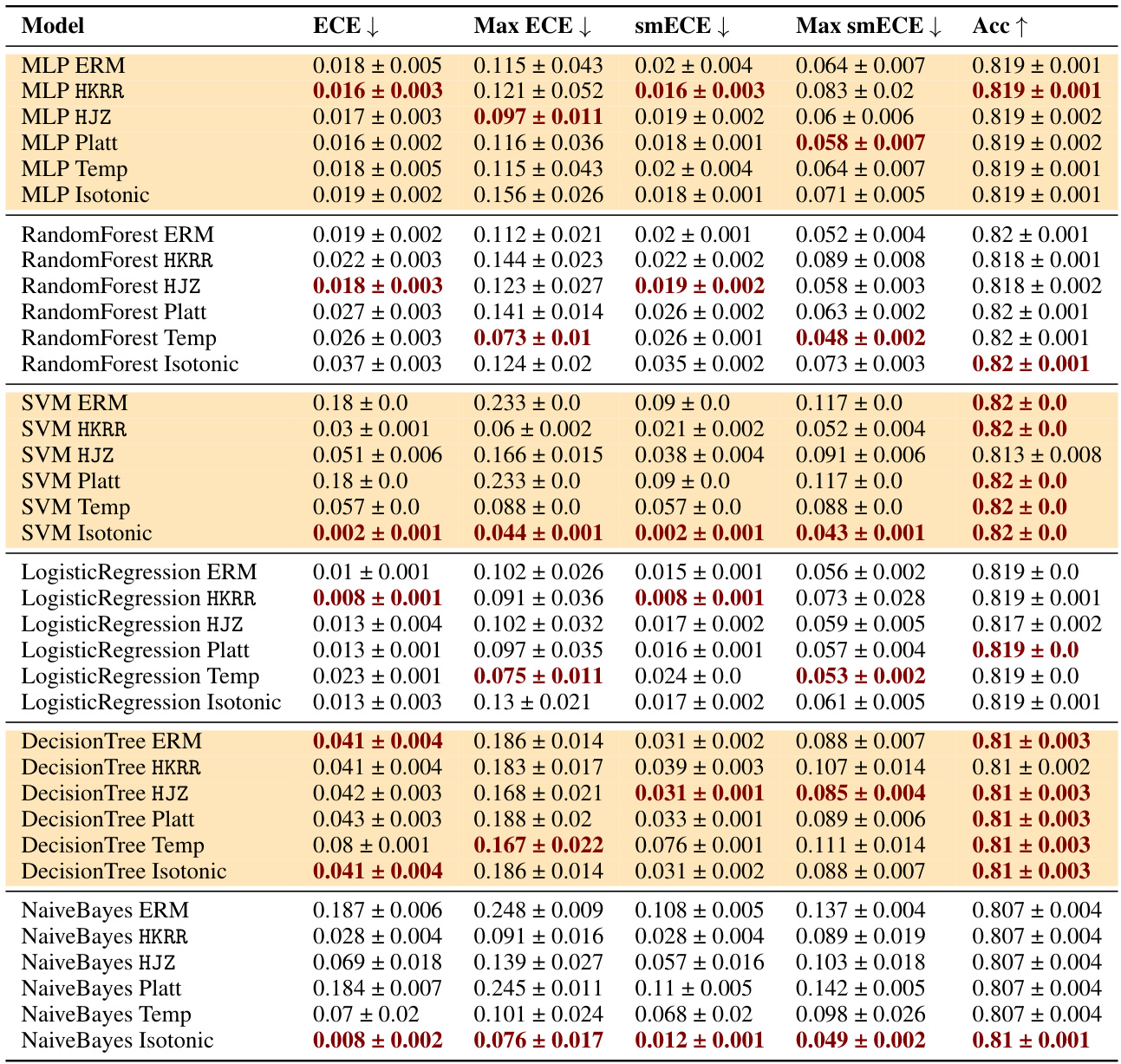
🔼 This table compares the performance of three families of methods for achieving multicalibration: standard ERM, ERM followed by a classical recalibration method, and ERM followed by an explicit multicalibration algorithm. The results are shown for multiple models (MLP, Random Forest, SVM, Logistic Regression, Decision Tree, Naive Bayes) on the MEPS dataset. The table highlights that models which are well-calibrated without post-processing (MLP, Random Forest, Logistic Regression) tend not to benefit from multicalibration, whereas uncalibrated models (SVM, Decision Trees, Naive Bayes) show improvements in worst-group calibration error with multicalibration post-processing. It also demonstrates the impact of the choice of calibration metric (ECE vs smECE) on the selection of the best method.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.
🔼 This table compares the performance of three multicalibration post-processing algorithms (HKRR, HJZ, and Isotonic Regression) against a standard ERM baseline on the MEPS dataset. It shows the ECE, max ECE, smECE, max smECE, and accuracy for various models. The results demonstrate that for well-calibrated models (like MLPs, random forests, and logistic regression), post-processing offers minimal to no improvement, while for uncalibrated models (SVMs, Decision Trees, Naive Bayes), multicalibration post-processing provides more significant gains. Notably, the choice between ECE and smECE as evaluation metrics can influence the selection of the best post-processing algorithm, highlighting the importance of metric selection.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.
🔼 This table shows the results of multicalibration post-processing algorithms (HKRR and HJZ) compared to the ERM baseline on the MEPS dataset. The best-performing hyperparameters for each algorithm were selected based on validation max smECE. The table highlights that calibrated models such as MLPs, random forests, and logistic regression benefit little from additional post-processing, while uncalibrated models such as SVMs, decision trees, and Naive Bayes see improvements. It also illustrates the impact of the choice of metric (ECE vs. smECE) on algorithm selection, demonstrating the need to carefully consider this choice in practice.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.
🔼 This table presents the results of an experiment comparing the performance of different multicalibration post-processing algorithms (HKRR, HJZ, Platt scaling, isotonic regression) against a standard ERM baseline for various machine learning models (MLP, Random Forest, SVM, Logistic Regression, Decision Tree, Naive Bayes) on the MEPS dataset. The table shows the average ECE (Expected Calibration Error), maximum ECE, average smECE (smoothed ECE), maximum smECE and test accuracy, each with standard deviations calculated from five independent train/validation splits. The results highlight the conditions under which multicalibration algorithms may or may not provide improvements over simpler methods like isotonic regression.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.
🔼 This table compares the performance of three families of methods for multicalibration: standard ERM, ERM followed by recalibration, and ERM followed by explicit multicalibration algorithms. It shows the impact of multicalibration post-processing on various machine learning models, highlighting that calibrated models often don’t need further processing, while uncalibrated ones benefit from multicalibration. The choice of metric for evaluating calibration error is also discussed, with an emphasis on the maximum calibration error across different subgroups.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.
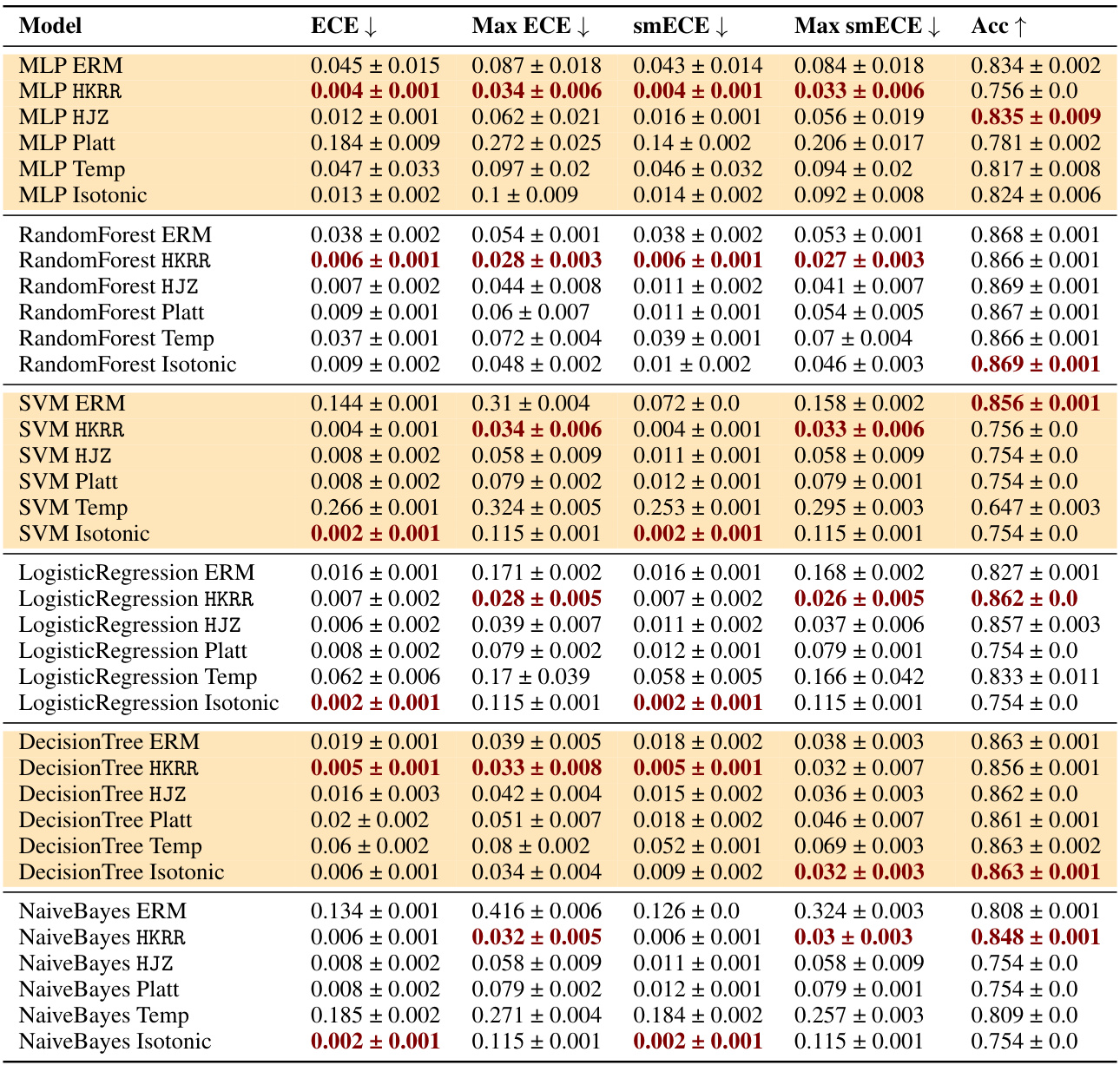
🔼 This table presents a comparison of the performance of three families of methods for achieving multicalibration on the MEPS dataset: standard ERM, ERM followed by a classical recalibration method, and ERM followed by an explicit multicalibration algorithm. The table shows the ECE, max ECE, smECE, max smECE, and accuracy for each method and model, highlighting the subtle differences in performance between methods and the importance of the choice of metric for evaluating results.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.

🔼 This table presents the results of comparing three families of methods for achieving multicalibration: standard ERM, ERM followed by recalibration, and ERM followed by explicit multicalibration. It shows the ECE, max ECE, smECE, max smECE and accuracy for several models (MLP, Random Forest, SVM, Logistic Regression, Decision Tree, Naive Bayes) on the MEPS dataset. The results highlight that models that are inherently well-calibrated (e.g., MLP, Random Forest, Logistic Regression) often do not benefit from additional multicalibration post-processing, while inherently uncalibrated models (e.g., SVM, Decision Tree, Naive Bayes) may see improvements using multicalibration. The table also illustrates the impact of choosing between the ECE and smECE metrics for selecting the best model.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.

🔼 This table presents a comparison of the performance of three multicalibration post-processing algorithms (HKRR, HJZ, and isotonic regression) against ERM on various machine learning models applied to the MEPS dataset. The best hyperparameters for each algorithm were selected based on validation max smECE. It highlights that well-calibrated models (MLP, Random Forest, Logistic Regression) may not require additional post-processing for multicalibration, while uncalibrated models (SVM, Decision Trees, Naive Bayes) benefit significantly from post-processing. The table further emphasizes that the choice of evaluation metric (ECE vs. smECE) influences algorithm selection for Decision Trees.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.
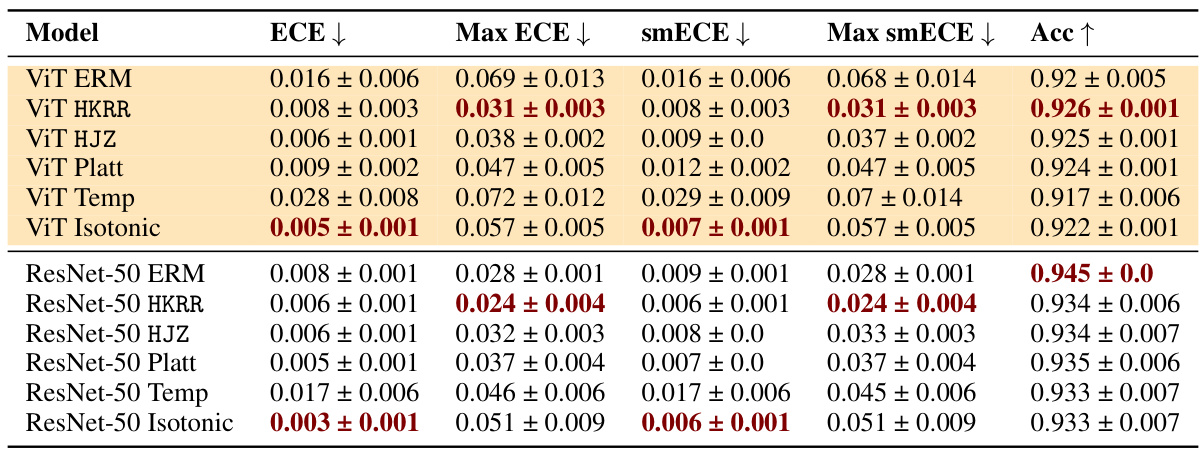
🔼 This table compares the performance of three families of methods for achieving multicalibration: standard ERM, ERM followed by a classical recalibration method, and ERM followed by an explicit multicalibration algorithm. The results are shown for multiple models (MLP, Random Forest, SVM, Logistic Regression, Decision Tree, Naive Bayes) on the MEPS dataset and using the metrics ECE, Max ECE, smECE, Max smECE and Accuracy. The table highlights how models that are already calibrated often don’t require additional multicalibration steps and emphasizes the sensitivity of multicalibration algorithms to hyperparameter choices and how choice of metric (ECE or smECE) can impact model selection.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.
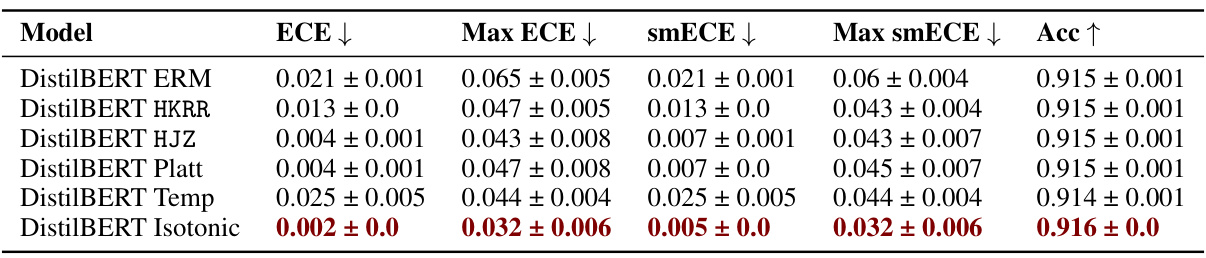
🔼 This table shows the test accuracy and maximum group-wise calibration error (smECE) for different machine learning models and post-processing methods on image and language datasets. It highlights the effectiveness of multicalibration post-processing in improving calibration, especially for large language models.
read the caption
Figure 4: Test accuracy vs. maximum group-wise calibration error (smECE) over three train/validation splits for ViT and DenseNet on Camelyon17, and DistilBERT on CivilComments. Multicalibration post-processing has scope for improvement in each setting, and does so with nearly no loss in accuracy. (Bottom): Impact of post-processing algorithms for Civil Comments (DistilBERT) and Amazon Polarity (ResNet-56). Multicalibration and isotonic regression both offer improvements to worst group calibration error. Full results are available in Appendix J.1.
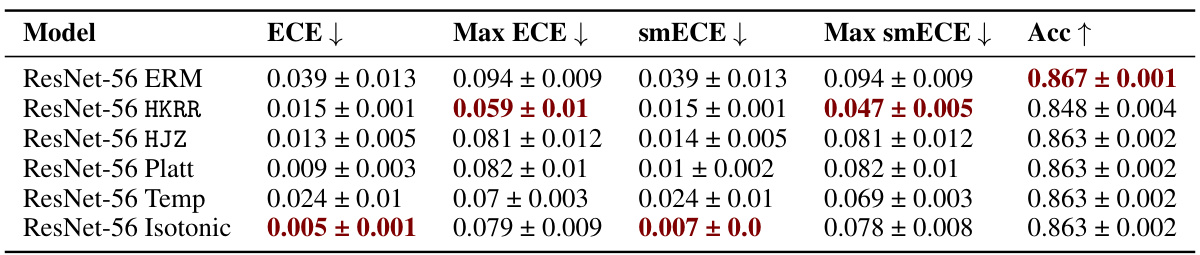
🔼 This table presents the results of applying multicalibration post-processing algorithms (HKRR and HJZ) and traditional calibration methods (Platt scaling, isotonic regression) to different machine learning models on the MEPS dataset. The best hyperparameters for each method, chosen based on validation performance, are reported. The table compares the performance of these methods across various metrics, including ECE, max ECE, smECE, max smECE, and accuracy. It highlights the finding that calibrated models, such as MLPs, random forests, and logistic regression, do not always benefit from further post-processing, and that the choice of metric (ECE vs. smECE) can significantly impact the selection of the best post-processing method. In contrast, uncalibrated models show improvements with multicalibration post-processing.
read the caption
Figure 2: Best performing HKRR and HJZ post-processing algorithm hyperparameters (selected based on validation max smECE) compared to ERM on the MEPS dataset. Calibrated models (MLP, random forest, logistic regression) need not be post-processed to achieve multicalibration. However, uncalibrated models (SVM, decision trees, naive Bayes) do benefit from multicalibration post-processing algorithms. Cells highlighted in blue show the importance of the choice of metric for selecting the best post-processing method for decision trees. Metric choice worst group ECE vs. worst group smECE can change which of ERM or HJZ is preferable.
Full paper#



















