↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Safe reinforcement learning (RL) is crucial for real-world applications but often suffers from sample inefficiency. Existing methods use a fixed sample size per iteration, leading to wasted samples in simple scenarios and insufficient exploration in complex ones. This creates a need for more efficient algorithms.
ESPO (Efficient Safe Policy Optimization) tackles this problem by dynamically adjusting the sample size based on the conflict between reward and safety gradients. It uses three optimization modes (reward maximization, cost minimization, and balance) to adapt the sampling strategy. This approach is theoretically proven to ensure convergence and stability while drastically improving sample efficiency and achieving better performance compared to state-of-the-art baselines on benchmark tasks. ESPO achieves substantial gains in sample efficiency, requiring 25-29% fewer samples and reducing training time by 21-38%.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses the critical issue of sample inefficiency in safe reinforcement learning. By introducing a novel sample manipulation technique, it significantly improves the efficiency and performance of existing safe RL algorithms. This contribution is highly relevant to researchers working on real-world applications of RL where safety is paramount, as it enables the development of more efficient and reliable safe RL agents. The theoretical analysis and empirical results provide a strong foundation for future research in this area, opening up new avenues for improving the sample complexity and stability of safe RL algorithms.
Visual Insights#
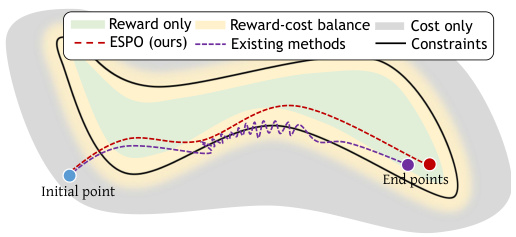
This figure illustrates the optimization trajectories of ESPO and existing safe RL methods across three optimization modes: reward-only, reward-cost balance, and cost-only. The different colored regions represent the dominance of each objective. ESPO’s trajectory (red dashed line) is smoother and more efficient, avoiding the oscillations seen in the existing methods (purple dashed line) which frequently cross boundaries between the optimization modes due to conflicts between safety and reward gradients. This highlights ESPO’s ability to dynamically adjust sample size based on gradient conflicts, leading to improved sample efficiency and stable optimization.
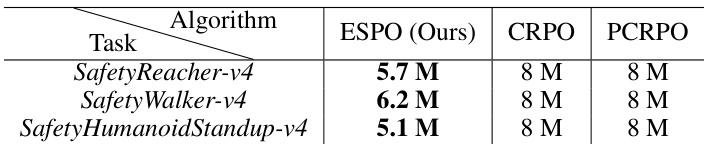
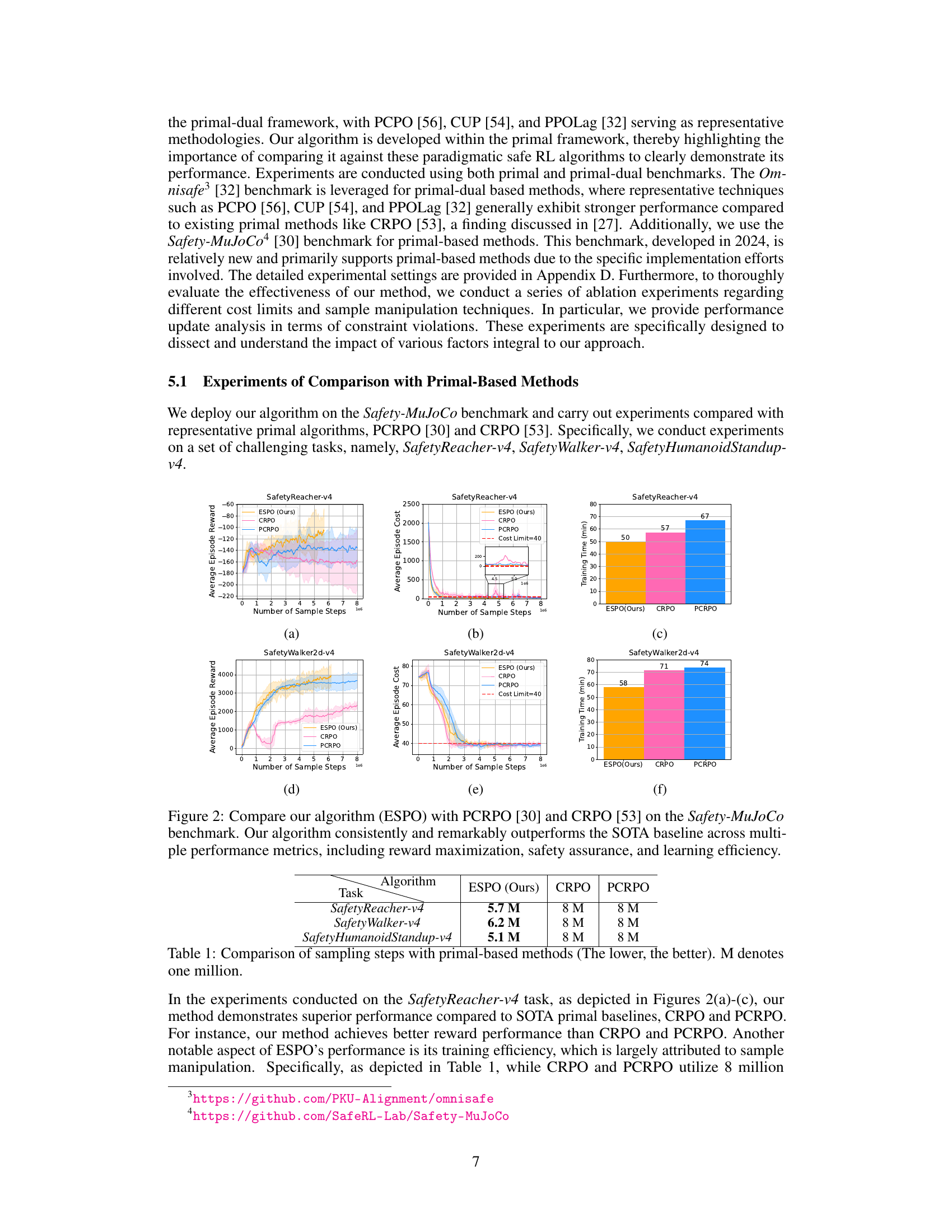
This table compares the number of sampling steps required by ESPO and two other primal-based safe RL algorithms (CRPO and PCRPO) across three different tasks from the Safety-MuJoCo benchmark. ESPO demonstrates superior sample efficiency, requiring fewer samples to achieve comparable or better performance.
In-depth insights#
Sample Manipulation#
The concept of ‘Sample Manipulation’ in reinforcement learning focuses on strategically altering the data used for training. Instead of using a fixed number of samples per iteration, this technique dynamically adjusts the sample size based on observed criteria, such as the conflict between reward and safety gradients. This adaptive approach aims to improve efficiency by reducing wasted samples in simple scenarios and enhancing exploration in complex situations where reward and safety objectives conflict. The core idea is to leverage gradient information to guide sample size adjustments, increasing the sample size when gradients conflict and decreasing it when alignment is observed. This dynamic sampling strategy is expected to reduce training time and improve sample complexity, leading to more efficient learning of safe and optimal policies. Theoretical analysis is essential to prove the convergence and stability of such methods, especially when dealing with complex constraints. The effectiveness of this technique hinges on the ability to accurately identify situations requiring increased exploration versus those allowing for efficient, reduced sampling. The success of ‘Sample Manipulation’ relies on carefully designing criteria for sample size adjustment that balance exploration, exploitation, and safety constraints.
Three-Mode Optimization#
The core idea of “Three-Mode Optimization” is to dynamically adapt the optimization strategy based on the interplay between reward and safety gradients. This adaptive approach enhances sample efficiency by avoiding wasted samples in simple scenarios and improving exploration in complex ones. The three modes — maximizing rewards, minimizing costs, and balancing the trade-off — allow for tailored sample size adjustment. Gradient alignment indicates a simpler optimization landscape, justifying fewer samples. Conversely, high gradient conflict necessitates more samples to resolve the conflict and achieve a stable balance between reward and safety. This dynamic sample manipulation is key to ESPO’s improved sample efficiency and optimization stability. The theoretical analysis supports this, proving convergence and providing sample complexity bounds. This three-mode strategy is not just an algorithmic tweak; it’s a fundamental shift in how safe RL handles conflicting objectives, offering a more efficient and robust approach than traditional methods.
ESPO Algorithm#
The Efficient Safe Policy Optimization (ESPO) algorithm is a novel approach to safe reinforcement learning that significantly improves sample efficiency. ESPO dynamically adjusts its sampling strategy based on the observed conflict between reward and safety gradients. This adaptive sampling technique avoids wasted samples in simple scenarios and ensures sufficient exploration in complex situations with high uncertainty or conflicting objectives. The algorithm uses a three-mode optimization framework: maximizing rewards, minimizing costs, and dynamically balancing the trade-off between them. This framework, coupled with the adaptive sampling, leads to substantial gains in sample efficiency and reduced training time, outperforming existing baselines by a considerable margin. Theoretically, ESPO guarantees convergence and improved sample complexity bounds, offering a robust and efficient solution for safe RL problems. The effectiveness of ESPO is demonstrated through experiments on various benchmarks, showcasing its ability to achieve superior reward maximization while satisfying safety constraints.
Theoretical Guarantees#
A strong theoretical foundation is crucial for any machine learning algorithm, and reinforcement learning (RL) is no exception. A section on “Theoretical Guarantees” would ideally delve into the mathematical underpinnings of the proposed safe RL method, providing rigorous proofs for its convergence, stability, and sample efficiency. This would involve demonstrating convergence rates, which quantify how quickly the algorithm approaches an optimal solution. Importantly, stability analysis would be needed to show that the algorithm remains robust to noise and uncertainties inherent in RL environments. Sample complexity bounds are also critical; they would specify the minimum number of samples required to achieve a certain level of performance, showcasing the algorithm’s efficiency compared to existing methods. Finally, the theoretical guarantees should consider the specific constraints of safe RL, rigorously proving that the algorithm satisfies safety constraints while maximizing rewards. A comprehensive theoretical analysis instills confidence in the algorithm’s reliability and performance and provides a deeper understanding beyond empirical results.
Future Work#
Future research directions stemming from this work on efficient safe reinforcement learning could explore several promising avenues. Extending the sample manipulation techniques to broader classes of safe RL algorithms, beyond primal-dual methods, would significantly expand the impact of this research. Investigating adaptive sample size strategies within different optimization landscapes could further refine the efficiency gains. Theoretical analysis should continue to provide stronger guarantees on convergence rates and sample complexity. Evaluating the robustness of the method across a wider variety of real-world environments, particularly those with significant uncertainties or high-dimensional state spaces, is also crucial for demonstrating the practical applicability of the proposed approach. Finally, developing more sophisticated conflict-resolution mechanisms within the three-mode framework could enhance the algorithm’s ability to handle complex trade-offs between reward maximization and safety constraints.
More visual insights#
More on figures
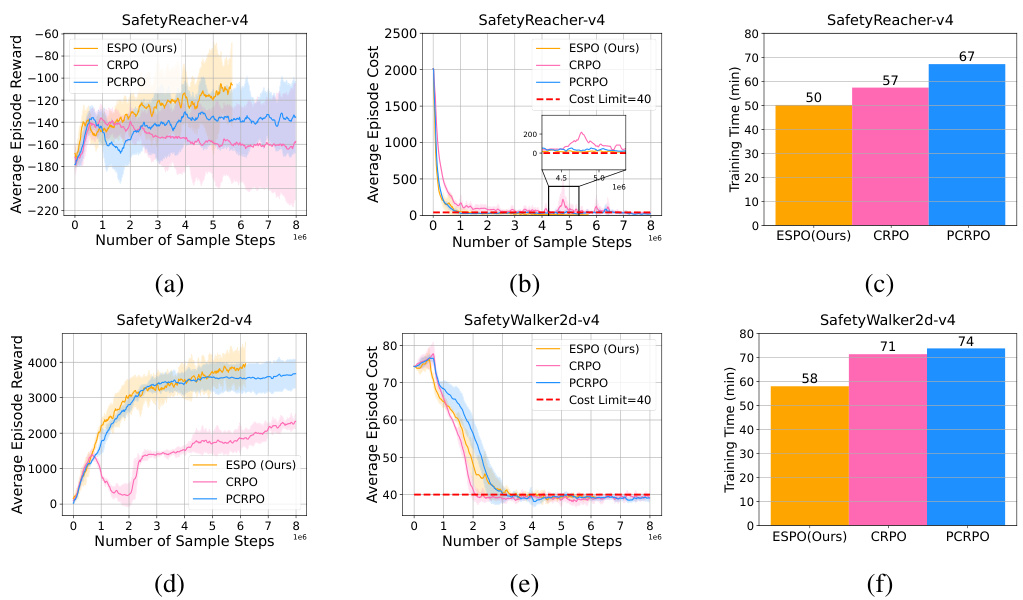
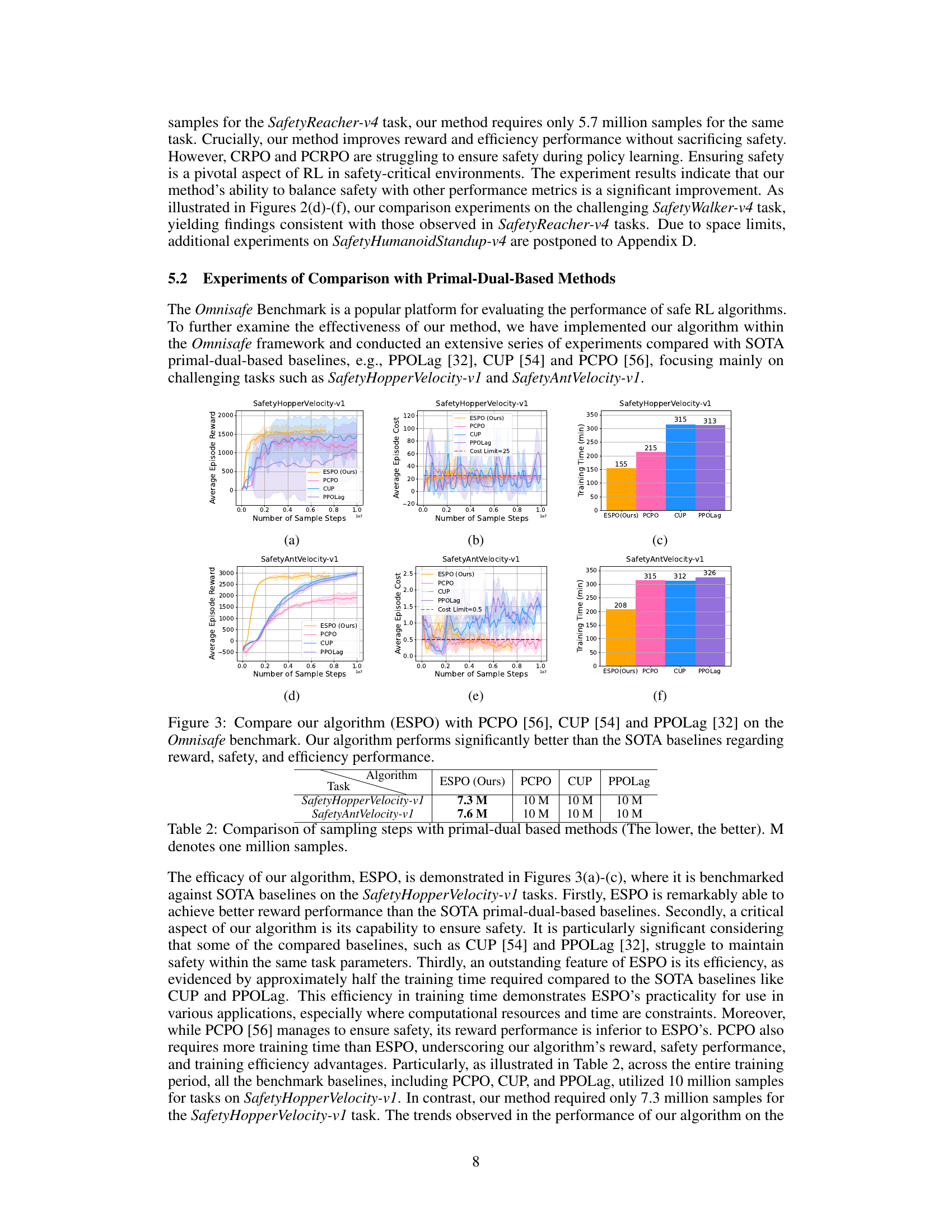
This figure compares the performance of the proposed ESPO algorithm with two state-of-the-art (SOTA) baselines, PCRPO and CRPO, across three different tasks within the Safety-MuJoCo benchmark. The results are presented in multiple subplots showing average episode reward, average episode cost, and training time (in minutes) for each algorithm on each task. ESPO consistently outperforms both PCRPO and CRPO in terms of reward maximization, maintaining safety (cost constraints), and showing significantly improved sample efficiency (fewer samples and faster training time).
This figure compares the performance of ESPO with two state-of-the-art primal-based safe RL algorithms (PCRPO and CRPO) across three different tasks from the Safety-MuJoCo benchmark. The plots show the average episode reward, average episode cost, and training time (in minutes) over the course of training, demonstrating that ESPO consistently achieves higher rewards while satisfying safety constraints, using significantly fewer samples and less training time.
This figure compares the performance of the proposed algorithm, ESPO, against two state-of-the-art (SOTA) baselines, PCRPO and CRPO, on three different tasks from the Safety-MuJoCo benchmark. The results demonstrate ESPO’s superiority across multiple metrics. Subfigures (a) and (d) show the average episode reward, showcasing ESPO’s superior reward maximization capabilities. Subfigures (b) and (e) illustrate the average episode cost, emphasizing ESPO’s robust safety assurance. Finally, subfigures (c) and (f) display the training time, highlighting ESPO’s improved learning efficiency. In summary, this figure provides strong empirical evidence of ESPO’s effectiveness in terms of reward performance, safety guarantees, and sample efficiency.
This figure presents a comparison of the proposed ESPO algorithm against two state-of-the-art (SOTA) primal-based safe reinforcement learning algorithms, PCRPO and CRPO, on three tasks from the Safety-MuJoCo benchmark. The results demonstrate that ESPO consistently outperforms the baselines in terms of average episode reward, average episode cost (i.e., safety), and training time. The improvement is significant across all three metrics, showcasing ESPO’s efficiency gains and enhanced safety capabilities.
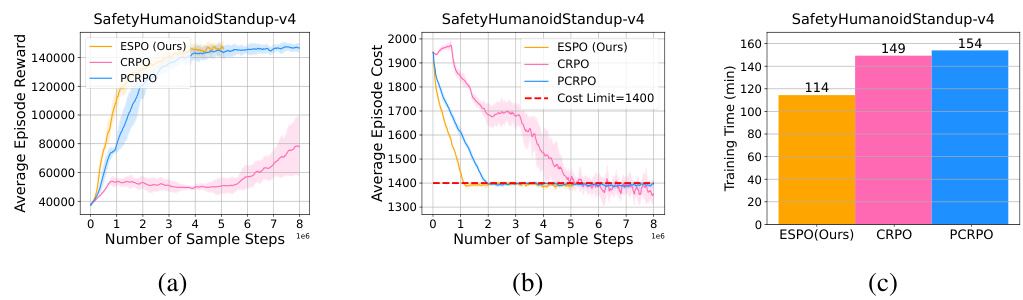
This figure compares the performance of ESPO with CRPO and PCRPO on the SafetyHumanoidStandup-v4 task, illustrating the average episode reward, average episode cost, and training time for each algorithm. It demonstrates that ESPO achieves a comparable reward to PCRPO while significantly outperforming CRPO in both reward and training time efficiency.
More on tables

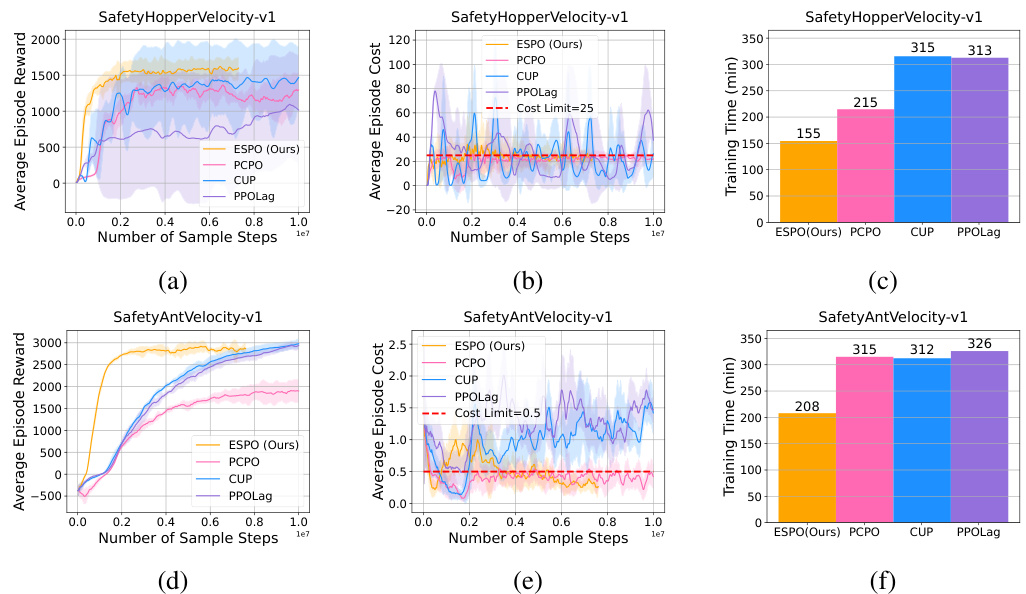
This table compares the number of samples required by ESPO and three primal-dual safe RL baselines (PCPO, CUP, PPOLag) to achieve a certain level of performance on two tasks from the Omnisafe benchmark (SafetyHopperVelocity-v1 and SafetyAntVelocity-v1). A lower number indicates better sample efficiency. The results show that ESPO requires significantly fewer samples than the baselines.

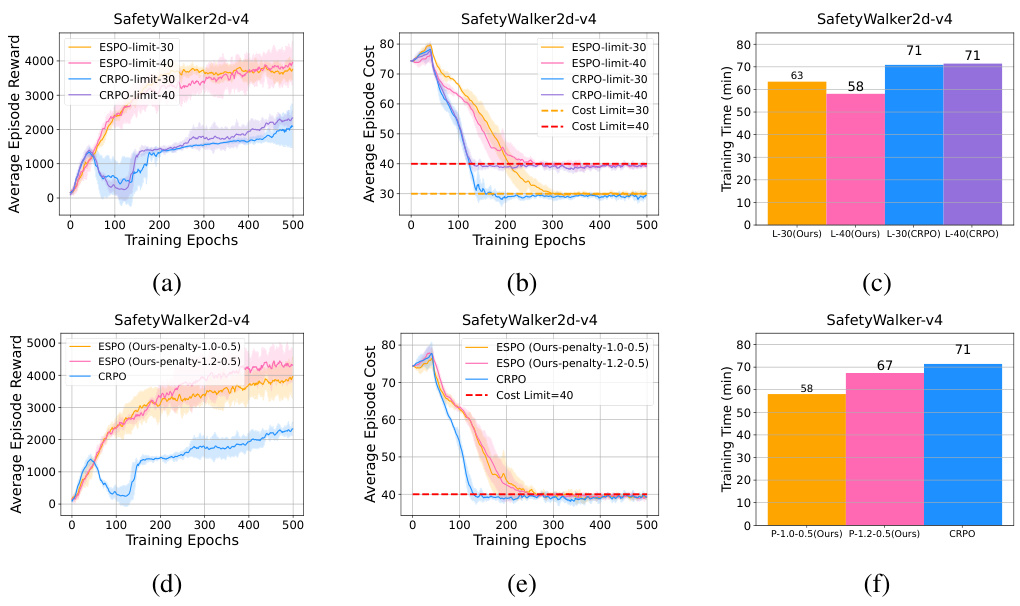
This table presents a comparison of the update styles between ESPO and CRPO algorithms for the SafetyHumanoidStandup-v4 task. It shows the number of times each algorithm focused solely on reward maximization, solely on cost minimization (due to safety violations), and simultaneously on both reward and cost. The results highlight the differences in optimization strategies employed by the two algorithms, which is further discussed in the paper.
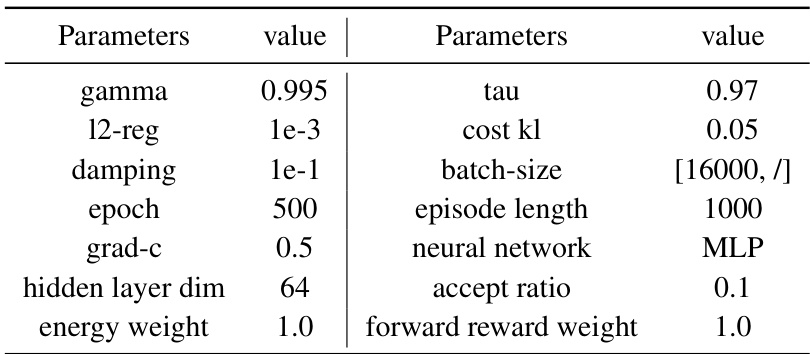
This table lists the key hyperparameters used for the experiments conducted on the Safety-MuJoCo benchmark. It includes parameters such as gamma, regularization strength (l2-reg), damping factor, epoch number, gradient clipping coefficient (grad-c), hidden layer dimensions in the neural network, acceptance ratio, energy weight, and forward reward weight. It also notes that the sample size in ESPO is determined dynamically by Algorithm 1 using Equations (7) and (6), where the base sample size (X) is set to 16000.

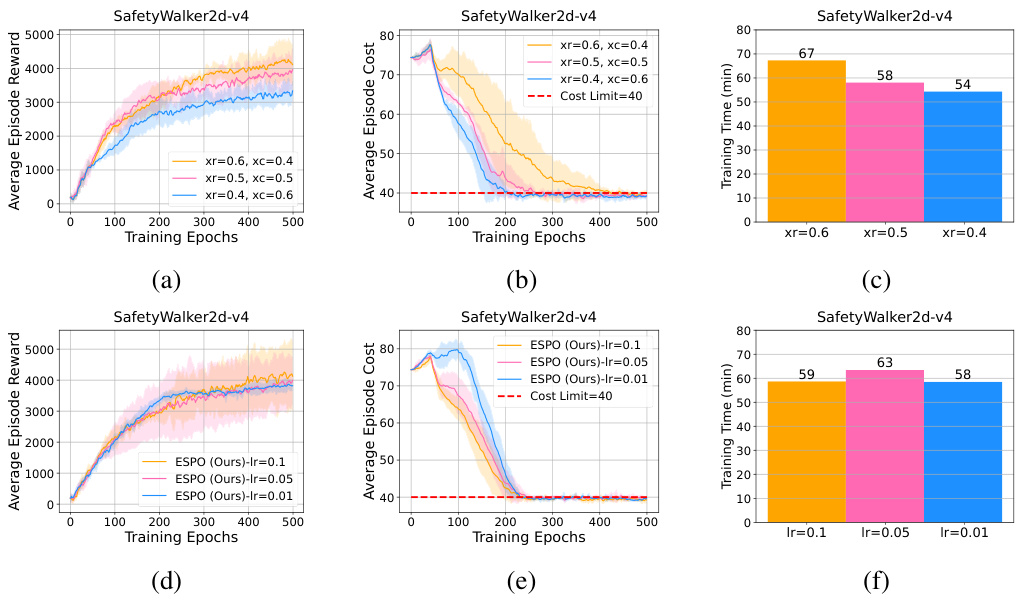
This table lists the sample parameters (ζ⁺, ζ⁻) used in the Omnisafe and Safety-MuJoCo experiments. These parameters influence the soft constraint region used in the three-mode optimization of the ESPO algorithm. The caption also cross-references the figures in the paper showing the results for each of the tasks listed.

This table lists the cost limit (b), positive slack (h+), and negative slack (h-) parameters used in the Safety-MuJoCo and Omnisafe benchmark experiments. It also cross-references the figures in the paper that display the results for each task.
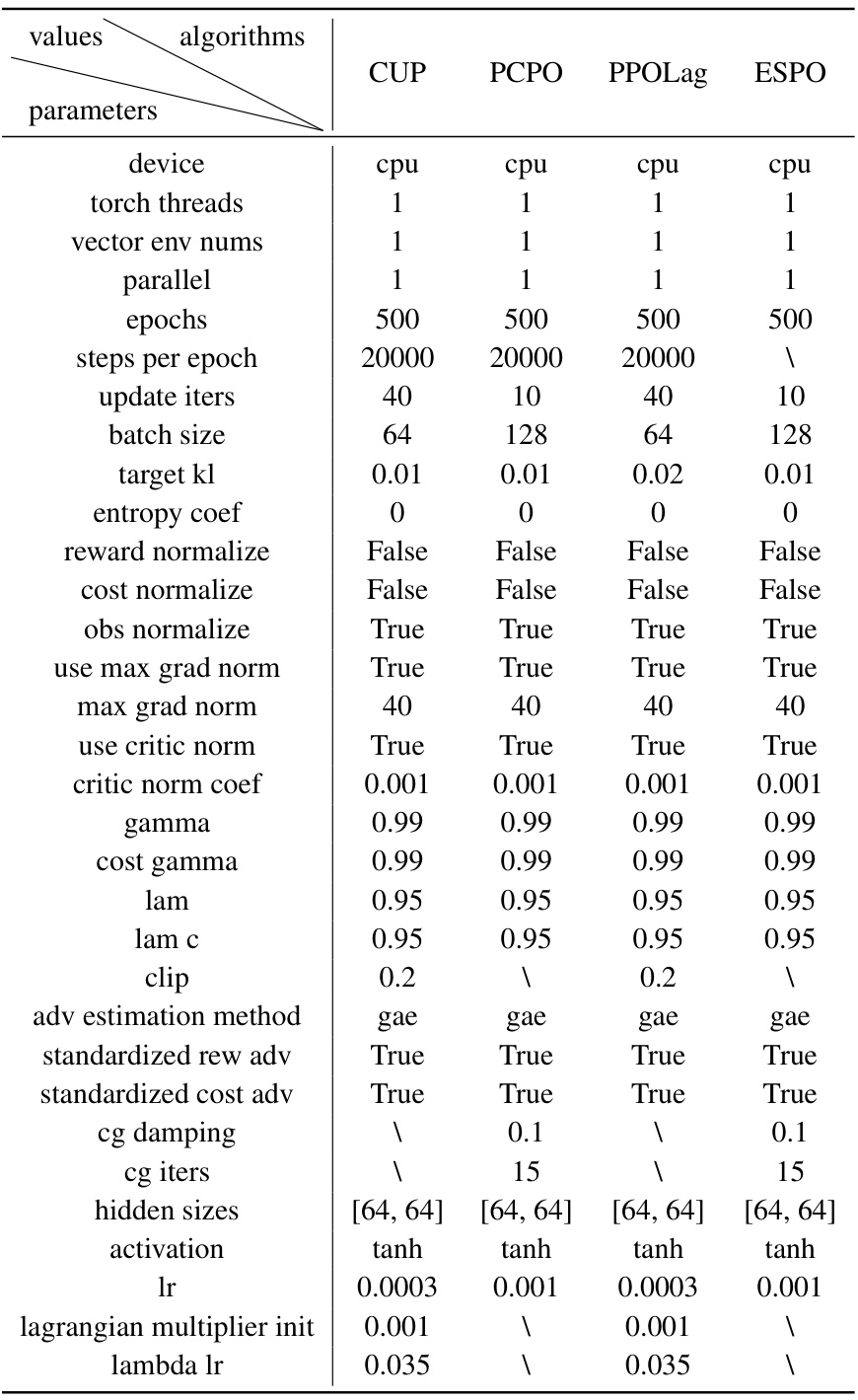
This table presents the hyperparameters used for the experiments conducted on the Omnisafe benchmark. It details the settings for ESPO and three other algorithms (CUP, PCPO, PPOLag). The table includes device, parallelisation specifics, epoch and step settings, hyperparameters related to the optimization process (target KL, entropy coefficient, gradient normalization, learning rates, etc.), and the method for advantage estimation. Importantly, it clarifies that ESPO’s sample size per epoch is dynamically adjusted using Equations (7) and (6) from Algorithm 1, and that baseline algorithms’ settings were consistent with the original Omnisafe benchmark and their performance was finely tuned for optimal results within the context of the benchmark.
Full paper#