TL;DR#
Many real-world reinforcement learning problems involve environments with latent factors that change over time. Existing meta-reinforcement learning (meta-RL) methods often struggle to adapt to these changes effectively. This paper addresses this issue by introducing DynaMITE-RL, a novel approach that models episode sessions—periods where the latent state remains constant.
DynaMITE-RL incorporates three key modifications to existing meta-RL algorithms: (1) Consistency of latent information within sessions, ensuring that the model makes use of the information accurately; (2) Session masking, focusing the model’s attention on relevant parts of the data during training; and (3) Prior latent conditioning, enabling the model to learn from temporal patterns in the changes of latent states. The results demonstrate that DynaMITE-RL significantly outperforms state-of-the-art meta-RL methods in various environments, including both discrete and continuous control tasks. This showcases the effectiveness of modeling temporal dynamics in handling environments with evolving latent contexts.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on reinforcement learning in dynamic environments. It introduces a novel approach that significantly improves performance in scenarios where latent factors change over time, a common challenge in real-world applications. The proposed framework, which incorporates session consistency, dynamics modeling of latent variables and session reconstruction masking, provides a robust solution for handling non-stationary latent states in both online and offline settings. This work opens up new avenues for addressing the challenges of temporal variation in RL applications such as robotics and recommender systems, where such variations are common.
Visual Insights#

🔼 This figure shows a graphical model and rollout of a dynamic latent contextual Markov decision process (DLCMDP). The left panel displays the model’s structure, highlighting the relationships between observed and latent variables such as states, actions, rewards, and latent contexts which change over time. The right panel illustrates a rollout of the DLCMDP, showing how sessions are defined by periods where the latent context remains fixed. Each session has a variable length, and transitions between sessions are governed by a latent transition function.
read the caption
Figure 1: (Left) The graphical model for a DLCMDP. The transition dynamics of the environment follows T(st+1,Mt+1 | St,at,mt). At every timestep t, an i.i.d. Bernoulli random variable, dt, denotes the change in the latent context, mt. Blue shaded variables are observed and white shaded variables are latent. (Right) A DLCMDP rollout. Each session i is governed by a latent variable m² which is changing between sessions according to a fixed transition function, Tm(m' | m). We denote li as the length of session i. The state-action pair (sį, a) at timestep t in session i is summarized into a single observed variable, x. We emphasize that session terminations are not explicitly observed.

🔼 This table presents the average single episode returns achieved by DynaMITE-RL and several other state-of-the-art meta-reinforcement learning algorithms across a diverse set of environments. The results highlight DynaMITE-RL’s superior performance, consistently achieving the highest average return and uniquely recovering the optimal policy in each environment. The number of seeds used for averaging varied slightly between environments.
read the caption
Table 1: Average single episode returns for DynaMITE-RL and other state-of-the-art meta-RL algorithms across different environments. Results for all environments are averaged across 5 seeds beside ScratchItch which has 3 seeds. DynaMITE-RL, in bold, achieves the highest return on all of the evaluation environments and is the only method able to recover an optimal policy.
In-depth insights#
Dynamic Latent Context#
The concept of “Dynamic Latent Context” introduces a significant advancement in reinforcement learning by addressing the limitations of static latent variable models. It acknowledges that in real-world scenarios, the underlying latent factors influencing an environment’s dynamics are not constant but evolve over time. This dynamism is crucial, as static models fail to capture the nuanced changes in an agent’s context, leading to suboptimal policies. The core idea is to model the latent context as a dynamic variable, allowing the agent to track its evolution and adjust its strategy accordingly. This involves effectively learning the dynamics of latent context transitions, allowing the agent to smoothly adapt its behavior to evolving conditions. Key challenges involve inferring the latent context from observed data, modeling the temporal structure of these changes (session consistency), and developing efficient learning algorithms to handle this increased complexity. Addressing these challenges will unlock the potential of reinforcement learning agents to effectively operate in dynamic, real-world environments.
Session-Based Consistency#
The concept of ‘Session-Based Consistency’ in the context of dynamic latent contextual Markov Decision Processes (DLCMDPs) introduces a crucial refinement to variational inference methods. It leverages the inherent property of DLCMDPs where latent states remain fixed within a ‘session’, a period between changes in the latent context. The approach introduces a consistency loss that penalizes discrepancies between the evolving posterior belief about the latent state during a session and the final posterior belief reached at the session’s conclusion. This penalty, therefore, enforces a monotonic improvement in the certainty of the model’s belief over time within the constant latent context. The practical implication is that the model learns to efficiently integrate observations and improve its estimates during each session, rather than potentially being distracted or misled by transitions to different contexts. By making the inference process more temporally coherent within a session, session-based consistency enhances the accuracy of the posterior and facilitates more effective policy learning. The approach’s effectiveness is underscored by experiments, showing clear improvements over baselines that don’t consider this form of consistency within the session structure.
Variational Inference#
Variational inference is a powerful technique for approximating intractable probability distributions, particularly relevant in complex machine learning models where exact inference is computationally prohibitive. The core idea is to approximate a complex, true posterior distribution with a simpler, tractable variational distribution. This is achieved by minimizing the Kullback-Leibler (KL) divergence between the two distributions, a measure of their dissimilarity. By minimizing this divergence, we effectively find the best-fitting variational distribution that captures the essential characteristics of the true posterior. A key advantage lies in its ability to handle high-dimensional data and complex models, making it suitable for diverse applications such as deep learning and Bayesian methods. However, the choice of the variational family is crucial, impacting the accuracy and efficiency of the approximation. Improper choices can lead to poor approximations or computational bottlenecks. Furthermore, the success hinges on the model’s ability to learn effective parameters for the variational distribution. Therefore, careful consideration of the variational family and appropriate optimization techniques are critical for successful implementation and achieving reliable results.
Meta-RL in DLCMDPs#
Meta-reinforcement learning (Meta-RL) in Dynamic Latent Contextual Markov Decision Processes (DLCMDPs) presents a unique challenge and opportunity. DLCMDPs model environments with latent states that evolve over time, unlike standard MDPs. This temporal evolution requires methods that can efficiently adapt to these changes, which is where Meta-RL excels. The core challenge lies in effectively inferring the latent context while simultaneously learning a policy robust to its variations. DynaMITE-RL addresses this by incorporating key modifications to existing Meta-RL algorithms: session consistency, session masking, and prior latent conditioning, all designed to exploit the temporal structure of sessions where the latent state remains constant. This approach is shown to significantly improve learning efficiency and performance compared to baselines on a variety of tasks, highlighting the potential of Meta-RL techniques to solve complex, dynamic real-world problems. The key advantage lies in tackling partially observable settings through structured modeling and inference, rather than treating the latent context as purely stochastic noise.
Ablation Studies#
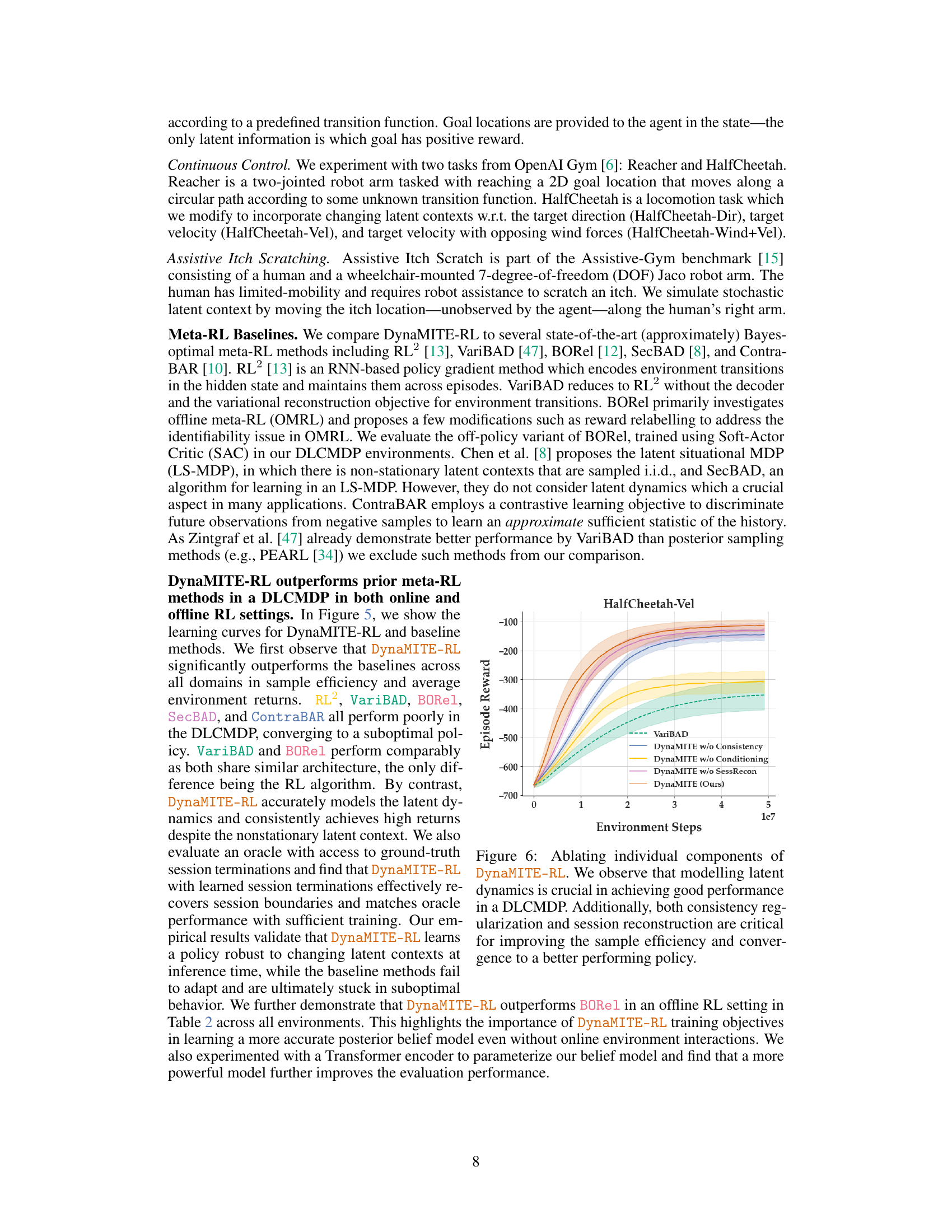
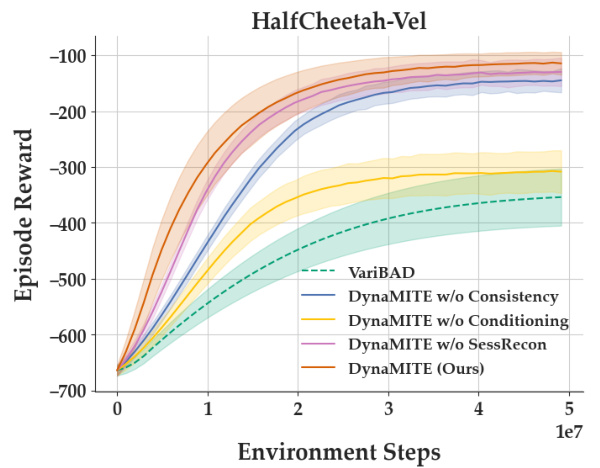
Ablation studies systematically remove components of a model to assess their individual contributions. In the context of DynaMITE-RL, this involved removing key elements: consistency regularization, latent belief conditioning, and session reconstruction masking. Removing consistency regularization resulted in suboptimal performance, highlighting its importance in improving posterior estimates by enforcing increasing information about the latent context within a session. Similarly, removing latent belief conditioning led to performance comparable to VariBAD, showing the crucial role of modeling latent dynamics for effective learning in dynamic environments. Lastly, omitting session reconstruction masking negatively impacted efficiency as the model unnecessarily attempted to reconstruct irrelevant transitions. These results strongly support the value of each proposed component in achieving DynaMITE-RL’s superior performance, demonstrating that they are not merely additive but synergistically work together to handle dynamic latent contexts effectively.
More visual insights#
More on figures
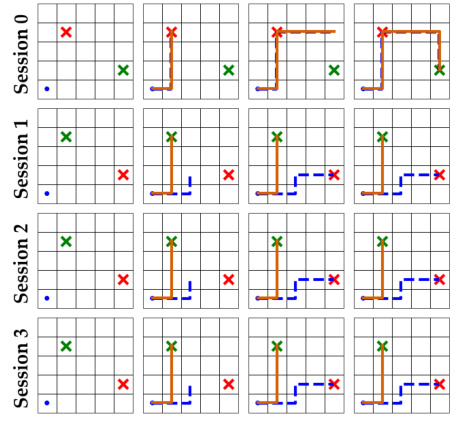
🔼 This figure compares the performance of VariBAD and DynaMITE-RL on a gridworld task where the goal location changes between sessions. VariBAD, which does not model the latent context dynamics, fails to adapt to these changes and gets stuck after reaching the goal in the first session. In contrast, DynaMITE-RL correctly infers the goal location transition and consistently reaches the goal in each session.
read the caption
Figure 2: VariBAD does not model the latent context dynamics and fails to adapt to the changing goal location. By contrast, DynaMITE-RL correctly infers the transition and consistently reaches the rewarding cell (green cross).

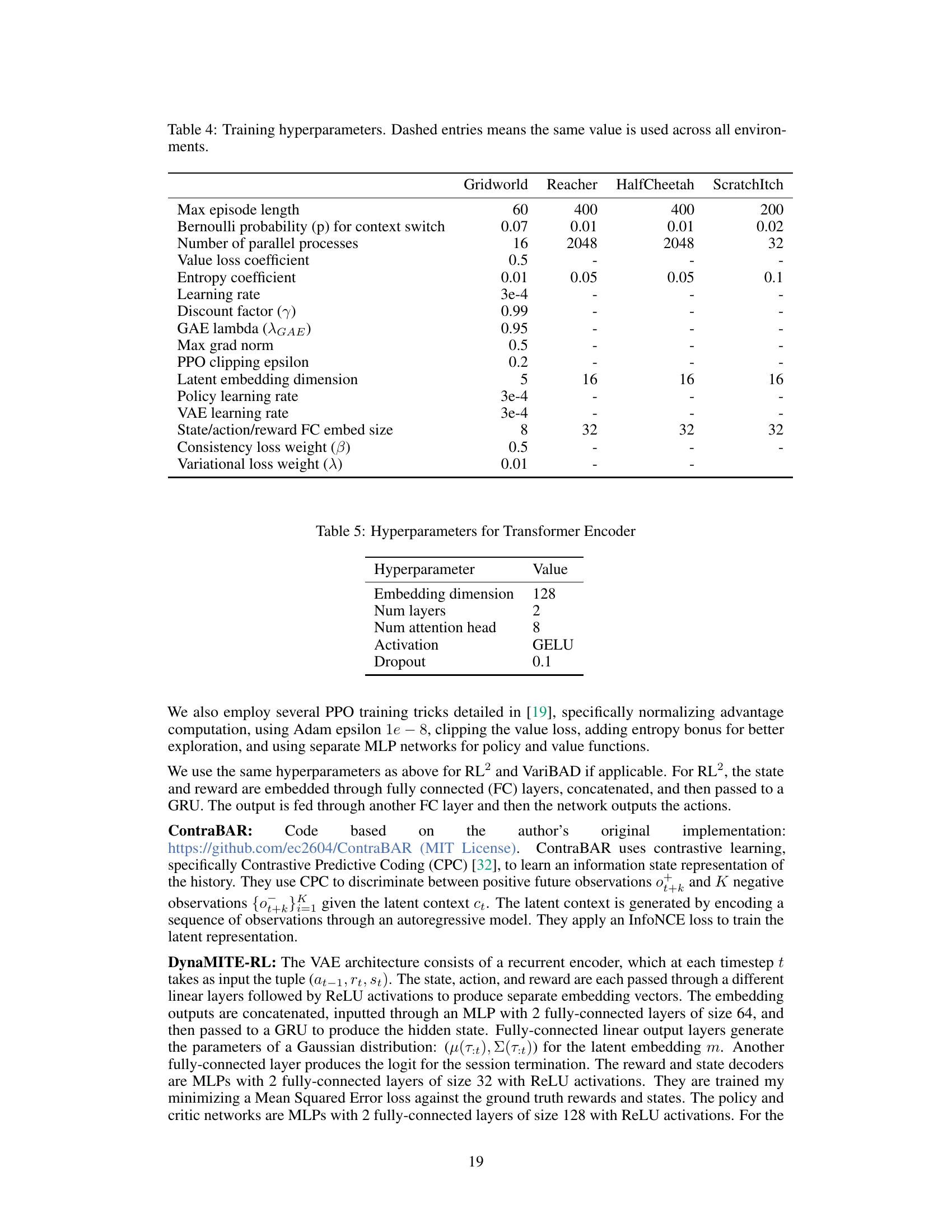
🔼 This figure shows the pseudocode for online training of DynaMITE-RL. The algorithm takes as input the environment, policy, critic, and belief model. It then collects DLCMDP episodes, trains the posterior belief model by maximizing ELBO, and trains the policy and critic with any online RL algorithm. The figure also shows the model architecture of DynaMITE-RL. The architecture consists of an inference network that takes as input the history of observations and outputs the posterior distribution over the latent context variables. The dynamics model takes as input the current state, action, and latent context and outputs the next state. The reward model takes as input the current state, action, and latent context and outputs the reward. The policy takes as input the current state and latent context and outputs the action. The critic takes as input the current state, action, and latent context and outputs the value.
read the caption
Figure 3: Pseudo-code (online RL training) and model architecture of DynaMITE-RL.

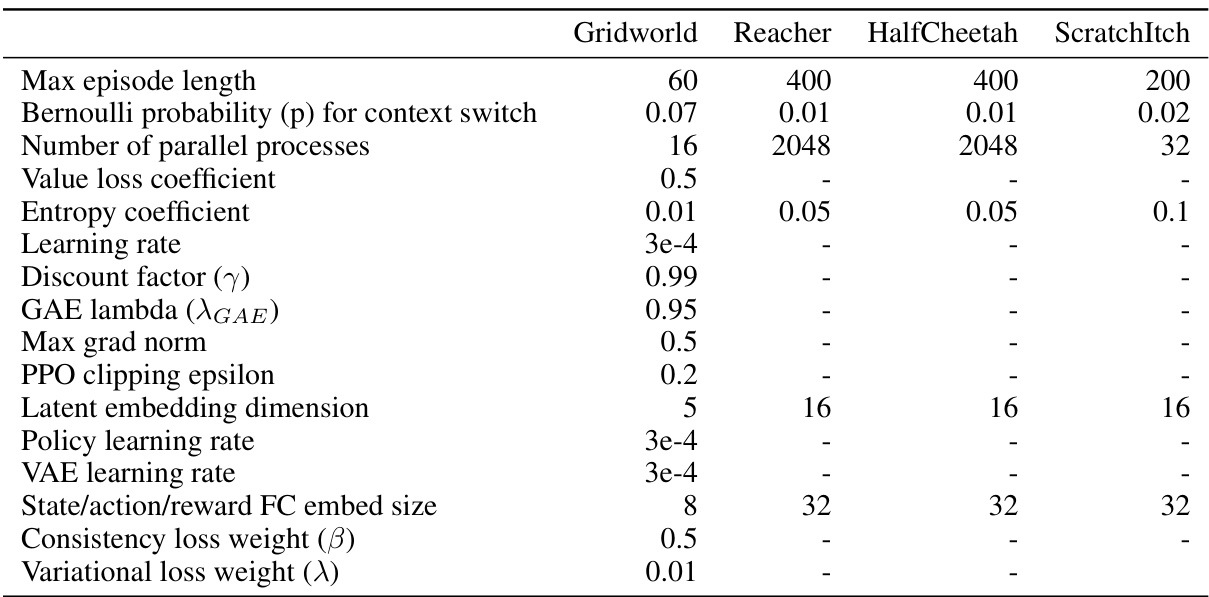
🔼 This figure shows four different reinforcement learning environments used to evaluate the DynaMITE-RL algorithm. The environments are designed to have changes in reward or dynamics between sessions, simulating real-world scenarios with non-stationary aspects. Specifically, the environments show (from left to right): a grid world with changing goal locations, a robotic arm reaching task with changing goal locations, a simulated cheetah running task with varying target velocities, and a robotic arm assisting a human in scratching an itch (where the location of the itch changes). These diverse scenarios showcase the ability of the DynaMITE-RL algorithm to adapt to dynamically changing environments.
read the caption
Figure 4: The environments considered in evaluating DynaMITE-RL. Each environment exhibits some change in reward and/or dynamics between sessions including changing goal locations (left and middle left), changing target velocities (middle right), and evolving user preferences of itch location (right).
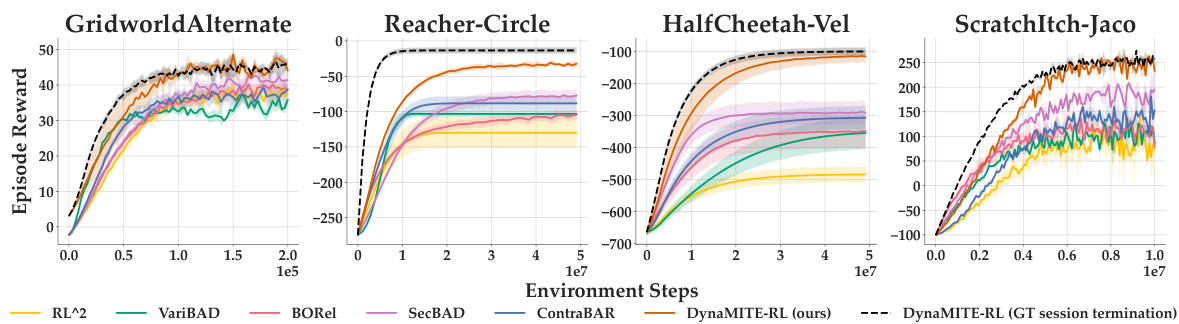
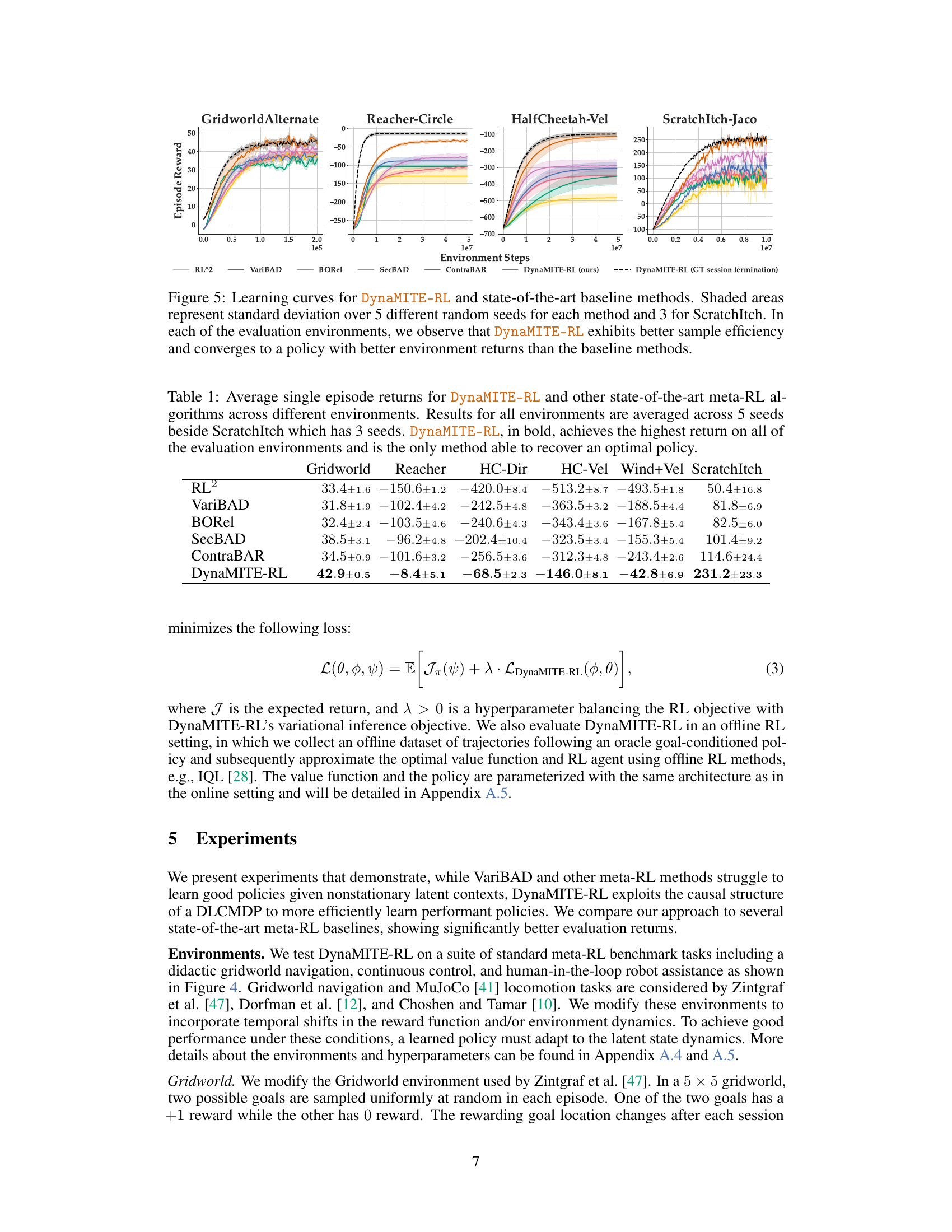
🔼 This figure shows the learning curves for DynaMITE-RL and several baseline methods across four different environments. The y-axis represents the episode reward, and the x-axis represents the number of environment steps. Shaded regions indicate the standard deviation across multiple random seeds. The results demonstrate that DynaMITE-RL achieves higher rewards and converges faster than the baselines in all four environments, highlighting its improved sample efficiency and performance.
read the caption
Figure 5: Learning curves for DynaMITE-RL and state-of-the-art baseline methods. Shaded areas represent standard deviation over 5 different random seeds for each method and 3 for ScratchItch. In each of the evaluation environments, we observe that DynaMITE-RL exhibits better sample efficiency and converges to a policy with better environment returns than the baseline methods.
🔼 This figure compares the learning curves of DynaMITE-RL against several state-of-the-art baseline methods across four different environments. The y-axis represents the episode reward, and the x-axis represents the number of environment steps. Shaded regions indicate the standard deviation across multiple random seeds. DynaMITE-RL consistently shows faster convergence and higher rewards compared to the baselines, highlighting its improved sample efficiency and superior performance.
read the caption
Figure 5: Learning curves for DynaMITE-RL and state-of-the-art baseline methods. Shaded areas represent standard deviation over 5 different random seeds for each method and 3 for ScratchItch. In each of the evaluation environments, we observe that DynaMITE-RL exhibits better sample efficiency and converges to a policy with better environment returns than the baseline methods.
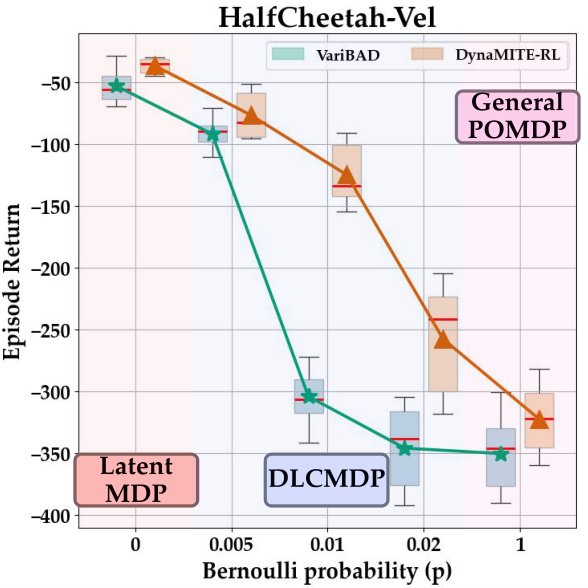
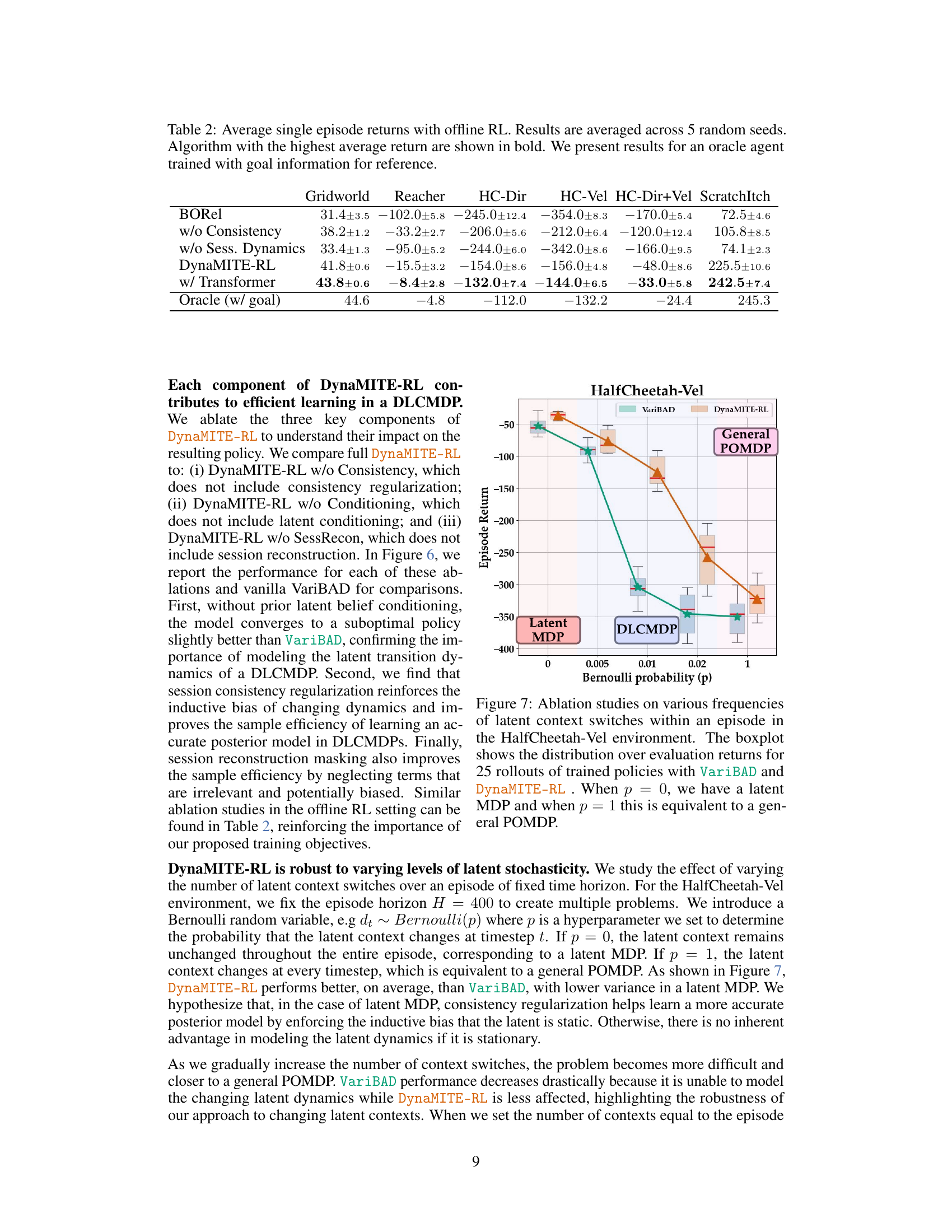
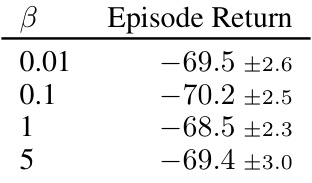
🔼 This figure shows the ablation study on various frequencies of latent context switches within an episode for the HalfCheetah-Vel environment. The boxplot displays the distribution of evaluation returns for 25 rollouts of trained policies using both VariBAD and DynaMITE-RL. The x-axis represents the Bernoulli probability (p) of a context switch at each time step. When p=0, there are no context switches (latent MDP), and when p=1, there’s a context switch at every step (general POMDP). The figure demonstrates the performance of both algorithms under varying degrees of latent context dynamism.
read the caption
Figure 7: Ablation studies on various frequencies of latent context switches within an episode in the HalfCheetah-Vel environment. The boxplot shows the distribution over evaluation returns for 25 rollouts of trained policies with VariBAD and DynaMITE-RL. When p = 0, we have a latent MDP and when p = 1 this is equivalent to a general POMDP.

🔼 This figure shows the pseudocode for the online RL training algorithm of DynaMITE-RL and its model architecture. The pseudocode outlines the steps involved in training the policy and critic using any online RL algorithm, collecting DLCMDP episodes, and training a posterior belief model. The architecture diagram illustrates the components of DynaMITE-RL: the inference network, dynamics model, reward model, policy, and critic. The inference network estimates the latent context variable and session termination. The dynamics and reward models predict the next state and reward given the current state, action, and latent context. The policy selects actions, and the critic evaluates the actions taken.
read the caption
Figure 3: Pseudo-code (online RL training) and model architecture of DynaMITE-RL.

🔼 This figure compares the learning curves of DynaMITE-RL and several state-of-the-art baseline methods across four different environments. The shaded regions represent the standard deviation over multiple runs, highlighting the consistency of DynaMITE-RL’s superior performance. DynaMITE-RL demonstrates better sample efficiency (faster learning) and achieves higher average rewards compared to the baselines.
read the caption
Figure 5: Learning curves for DynaMITE-RL and state-of-the-art baseline methods. Shaded areas represent standard deviation over 5 different random seeds for each method and 3 for ScratchItch. In each of the evaluation environments, we observe that DynaMITE-RL exhibits better sample efficiency and converges to a policy with better environment returns than the baseline methods.
More on tables

🔼 This table presents the average single episode returns achieved by DynaMITE-RL and several other state-of-the-art meta-reinforcement learning algorithms across five different simulated environments. The results are averaged over multiple random seeds (5 for most environments, 3 for ScratchItch). The table highlights DynaMITE-RL’s superior performance, consistently achieving the highest returns and uniquely recovering an optimal policy in all environments.
read the caption
Table 1: Average single episode returns for DynaMITE-RL and other state-of-the-art meta-RL algorithms across different environments. Results for all environments are averaged across 5 seeds beside ScratchItch which has 3 seeds. DynaMITE-RL, in bold, achieves the highest return on all of the evaluation environments and is the only method able to recover an optimal policy.
🔼 This table compares the average single episode returns achieved by DynaMITE-RL and several other state-of-the-art meta-reinforcement learning algorithms across a range of environments. The results are averaged over multiple runs (5 for most, 3 for ScratchItch). DynaMITE-RL consistently outperforms the baselines, achieving the highest return in every environment and being the only method able to find an optimal policy.
read the caption
Table 1: Average single episode returns for DynaMITE-RL and other state-of-the-art meta-RL algorithms across different environments. Results for all environments are averaged across 5 seeds beside ScratchItch which has 3 seeds. DynaMITE-RL, in bold, achieves the highest return on all of the evaluation environments and is the only method able to recover an optimal policy.
🔼 This table presents the average single episode returns achieved by DynaMITE-RL and several other state-of-the-art meta-reinforcement learning algorithms across various environments. The results are averaged over multiple random seeds (5 for most environments, 3 for ScratchItch). The table highlights that DynaMITE-RL consistently outperforms the other methods, achieving the highest average returns and uniquely achieving an optimal policy in all environments.
read the caption
Table 1: Average single episode returns for DynaMITE-RL and other state-of-the-art meta-RL algorithms across different environments. Results for all environments are averaged across 5 seeds beside ScratchItch which has 3 seeds. DynaMITE-RL, in bold, achieves the highest return on all of the evaluation environments and is the only method able to recover an optimal policy.
🔼 This table presents the average single episode returns achieved by DynaMITE-RL and several other state-of-the-art meta-reinforcement learning algorithms across a range of different environments. The results highlight DynaMITE-RL’s superior performance, consistently achieving the highest average return and being the only algorithm capable of recovering an optimal policy in all tested environments. The number of seeds used for averaging varied between 3 and 5 across the different environments.
read the caption
Table 1: Average single episode returns for DynaMITE-RL and other state-of-the-art meta-RL algorithms across different environments. Results for all environments are averaged across 5 seeds beside ScratchItch which has 3 seeds. DynaMITE-RL, in bold, achieves the highest return on all of the evaluation environments and is the only method able to recover an optimal policy.
Full paper#