TL;DR#
Current causal discovery methods often struggle with real-world datasets containing a mix of linear and nonlinear relationships, limiting their accuracy. Many existing techniques are restricted to datasets with only one type of relationship, leading to suboptimal results when applied to more complex scenarios. This creates a significant need for a more robust and versatile approach that can accurately identify causal links across different relationship types.
To address this, the authors propose Causal Discovery with Parent Score (CaPS). CaPS uses a novel unified criterion to identify topological ordering, regardless of the nature of relationships. A key innovation is the incorporation of a “parent score” metric that quantifies the strength of causal effects, accelerating the pruning process and improving the accuracy of predictions. Extensive experiments using synthetic and real-world data demonstrate that CaPS outperforms current state-of-the-art methods in accuracy and efficiency.
Key Takeaways#
Why does it matter?#
This paper is crucial because it presents CaPS, a novel algorithm that effectively handles both linear and nonlinear relationships in causal discovery, a significant improvement over existing methods which often assume pure linear or nonlinear relations. This addresses a critical limitation in real-world data analysis where mixed relationships are common, enabling more accurate causal inference and broader applicability across various domains. The introduction of the “parent score” further enhances the efficiency and accuracy of the algorithm.
Visual Insights#

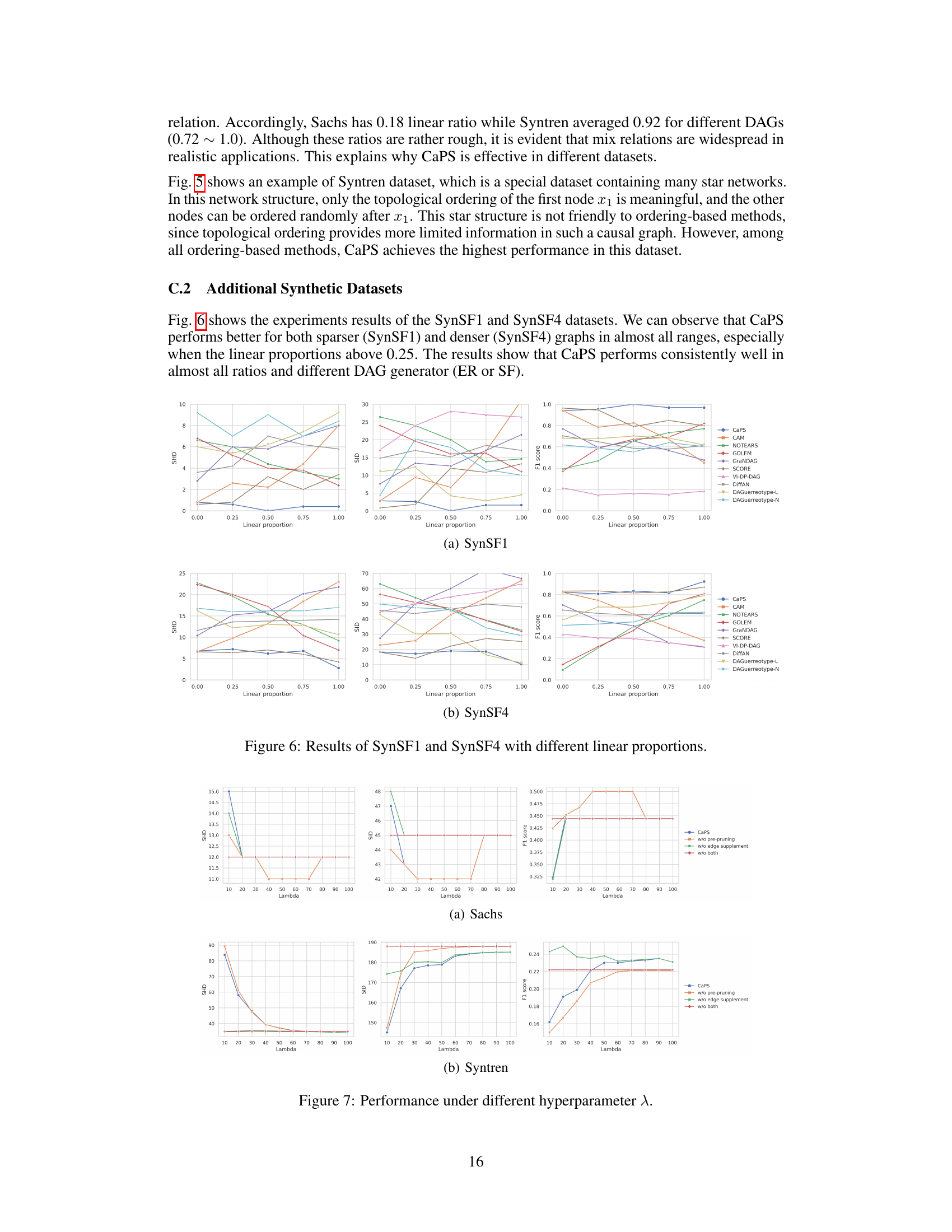
🔼 The figure compares the performance of three causal discovery methods (GOLEM, SCORE, and CaPS) on synthetic datasets with varying proportions of linear and nonlinear relationships. GOLEM is designed for linear relationships, SCORE for nonlinear relationships, and CaPS aims to handle both. The results show that GOLEM performs poorly when the linear ratio is low, SCORE performs poorly when the linear ratio is high, while CaPS shows consistent performance across different linear proportions.
read the caption
Figure 1: Performance of different solutions under datasets with different linear proportions. Since we don't know whether the real data is linear or nonlinear, it is difficult to choose an effective model. Thus, we need a method that works well in both linear and nonlinear and most possibly mixed cases.
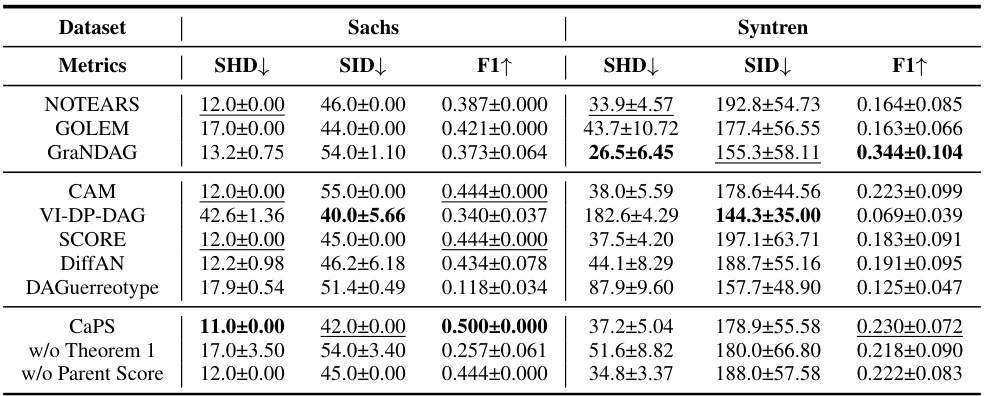
🔼 This table presents the performance of CaPS and other causal discovery methods on two real-world datasets: Sachs and Syntren. The metrics used to evaluate performance are Structural Hamming Distance (SHD), Structural Intervention Distance (SID), and F1 score. Lower SHD and SID values indicate better performance, while higher F1 scores indicate better performance. The table also includes ablation studies for CaPS, showing the impact of key components such as the topological ordering criterion and the parent score.
read the caption
Table 1: Results of real-world datasets, including three methods based on acyclicity constraint and five ordering-based methods. More baselines are given in Appendix C.4.
In-depth insights#
Causal Order Criterion#
A causal order criterion aims to establish a reliable sequence for causal relationships within a dataset. It’s crucial for causal discovery algorithms, as determining the correct order helps distinguish cause and effect, preventing the erroneous modeling of reversed relationships. Effective criteria often incorporate assumptions about the data’s underlying structure (e.g., linearity, specific noise distributions), but robust methods strive to be less sensitive to such assumptions, handling diverse datasets effectively. The ideal criterion would accurately reflect the strength of causal influence, potentially through metrics quantifying the average causal effect, facilitating efficient pruning of the causal graph and reducing computational complexity. Robustness and efficiency are key considerations when evaluating different causal order criteria.
Parent Score Metric#
The proposed “Parent Score Metric” offers a novel approach to causal discovery by quantifying the strength of causal relationships. Unlike existing methods that often rely on assumptions of purely linear or nonlinear relations, this metric leverages the average causal effect from a parent node to its children, providing a unified criterion for both linear and nonlinear scenarios. This is particularly valuable for real-world datasets, which frequently exhibit a mix of relationships. By incorporating the concept of parent score into the post-processing optimization phase, the algorithm is able to accelerate the pruning process and improve accuracy. The metric’s effectiveness stems from its ability to reflect the average causal effect regardless of the underlying functional form, thereby significantly improving the robustness and performance of causal discovery algorithms in complex datasets.
Unified Causal Learning#
Unified causal learning aims to overcome limitations of existing methods that focus solely on linear or nonlinear relationships. Current approaches often struggle when datasets contain a mixture of both. A unified framework could improve the accuracy and applicability of causal discovery, enabling analysis of real-world scenarios that are rarely purely linear or nonlinear. Key challenges include developing algorithms that can effectively handle diverse data types and integrating various identification criteria and assumptions within a single coherent model. This necessitates a comprehensive evaluation across diverse benchmark datasets and real-world applications to demonstrate the generalizability and robustness of the proposed solutions. A unified approach also promises to reduce the need for prior assumptions about the underlying data, making causal discovery more accessible and reliable across a broader range of scientific domains.
Synthetic Data Results#
A Synthetic Data Results section would ideally present a thorough evaluation of a causal discovery method’s performance on datasets with controlled characteristics. This would involve generating synthetic data with varying properties, such as the number of variables, the presence of both linear and nonlinear relationships, and different noise levels. Key results to highlight would include the accuracy metrics (SHD, SID, F1 score) achieved by the proposed method compared to established baselines. Visualizations like graphs showing performance trends across different data characteristics are crucial for understanding the method’s strengths and limitations. A discussion of how the method handles varying ratios of linear and nonlinear relations is vital, as this is often a challenge for existing causal discovery techniques. The analysis should not only focus on the overall performance, but also on the method’s ability to correctly identify causal directions and avoid false positives. A detailed analysis of the effect of varying data characteristics on the performance would strengthen the findings. Finally, the use of diverse data generation models (e.g., Erdos-Renyi, Scale-free) can offer insights into the robustness of the method across different causal structures.
Future Research#
Future research directions stemming from this ordering-based causal discovery method (CaPS) could explore several promising avenues. Extending CaPS to handle more complex causal relationships, such as those involving latent confounders or feedback loops, would significantly enhance its applicability to real-world scenarios. Investigating the impact of different noise distributions beyond the additive noise model assumed by CaPS is crucial to assess its robustness and generalizability. Furthermore, developing more efficient algorithms for high-dimensional data would be beneficial, potentially leveraging techniques like distributed computing or dimensionality reduction. Finally, a thorough exploration of CaPS’s theoretical limitations and a comparison with other causal discovery approaches under various scenarios would strengthen its position within the broader causal inference field. These enhancements could make CaPS a more versatile and reliable tool for diverse applications.
More visual insights#
More on figures

🔼 This figure compares the performance of three causal discovery algorithms: GOLEM (for linear relations), SCORE (for nonlinear relations), and the proposed CaPS algorithm (designed to handle both linear and nonlinear relations) on synthetic datasets with varying proportions of linear and nonlinear causal relationships. The results show that GOLEM performs poorly when the linear relation ratio is low, and SCORE performs poorly when the linear ratio is high. In contrast, CaPS demonstrates consistent performance across a wide range of linear proportions, highlighting its ability to effectively handle datasets with mixed linear and nonlinear relationships.
read the caption
Figure 1: Performance of different solutions under datasets with different linear proportions. Since we don't know whether the real data is linear or nonlinear, it is difficult to choose an effective model. Thus, we need a method that works well in both linear and nonlinear and most possibly mixed cases.
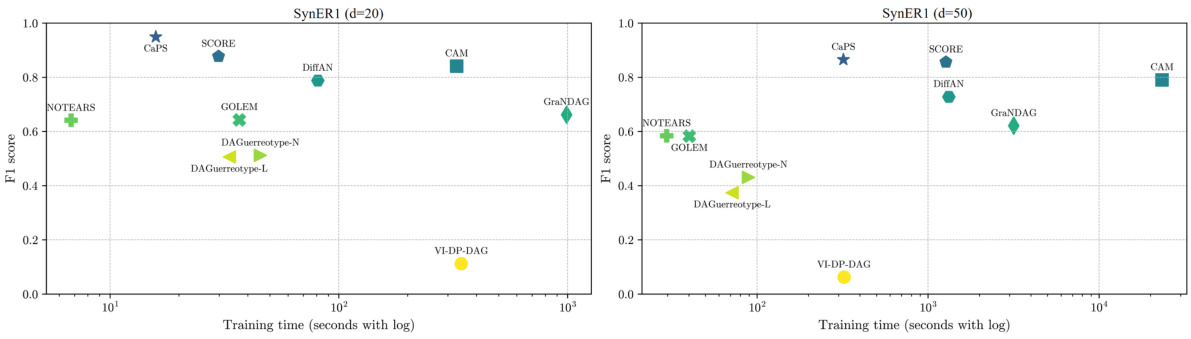
🔼 This figure compares the F1 score and training time of different causal discovery methods on the SynER1 dataset with larger-scale causal graphs (d=20 and d=50). The x-axis represents the training time (in seconds, logarithmic scale), and the y-axis represents the F1 score. It showcases CaPS’s competitive performance and training time compared to other methods, especially in larger graphs.
read the caption
Figure 3: F1 score and training time of SynER1 with larger-scale causal graph.

🔼 This figure visualizes the results of causal discovery on the SynER1 dataset, comparing the performance of CaPS (Causal Discovery with Parent Score) against a previous method. The leftmost panel shows the ground truth weighted directed acyclic graph (DAG) representing the true causal relationships between variables. The middle panel displays the DAG learned by a previous method, highlighting false predictions in red. The rightmost panel illustrates the DAG generated by CaPS, demonstrating fewer errors and a closer alignment to the ground truth. The color intensity in the heatmaps of the DAGs represents the strength of the causal effects, with darker colors indicating stronger effects. The quantitative metrics (SHD, SID, and F1 score) are shown for each DAG, reflecting the accuracy of the causal structure learning methods.
read the caption
Figure 4: Visualization on SynER1 dataset. Darker colors indicate stronger causal effects.
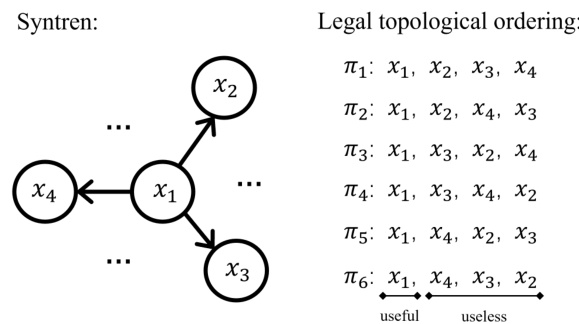
🔼 The figure displays the performance comparison of three causal discovery methods (GOLEM, SCORE, and CaPS) across synthetic datasets with varying proportions of linear and nonlinear relationships. GOLEM, designed for linear relations, performs poorly when the linear relation ratio is low. SCORE, designed for nonlinear relations, performs poorly when the linear ratio increases. In contrast, CaPS demonstrates consistent performance across the range of linear proportions, highlighting its ability to handle mixed linear and nonlinear relationships.
read the caption
Figure 1: Performance of different solutions under datasets with different linear proportions. Since we don't know whether the real data is linear or nonlinear, it is difficult to choose an effective model. Thus, we need a method that works well in both linear and nonlinear and most possibly mixed cases.

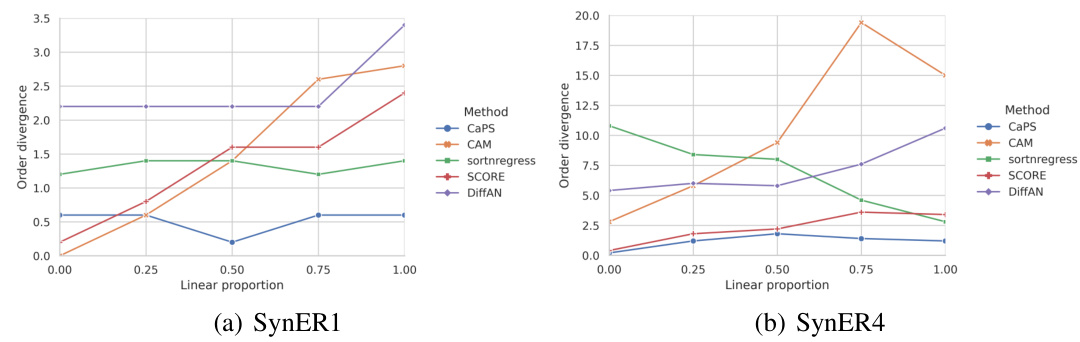
🔼 The figure displays the performance comparison of CaPS and eight other causal discovery methods across synthetic datasets SynER1 and SynER4. These datasets vary in the proportion of linear and nonlinear relationships, ranging from purely nonlinear (0.0) to purely linear (1.0). The plots show the SHD (Structural Hamming Distance), SID (Structural Intervention Distance), and F1 score for each method under different linear relationship ratios. This visualization helps assess how well each method performs across a spectrum of data characteristics, revealing its robustness to variations in data composition.
read the caption
Figure 2: Results of SynER1 and SynER4 with different linear proportions, where linear proportion equal to 0.0 means all relations are nonlinear and 1.0 means all relations are linear.

🔼 This figure shows the performance comparison of three causal discovery methods: GOLEM (for linear relations), SCORE (for nonlinear relations), and CaPS (the proposed method) on synthetic datasets with varying proportions of linear and nonlinear causal relations. The results demonstrate that GOLEM performs poorly when the linear relation ratio is low, and SCORE performs poorly when the linear relation ratio is high. In contrast, CaPS achieves relatively consistent performance across different linear relation ratios, indicating its effectiveness in handling datasets with both linear and nonlinear relations.
read the caption
Figure 1: Performance of different solutions under datasets with different linear proportions. Since we don't know whether the real data is linear or nonlinear, it is difficult to choose an effective model. Thus, we need a method that works well in both linear and nonlinear and most possibly mixed cases.

🔼 The figure shows the performance comparison of three causal discovery methods (GOLEM, SCORE, and CaPS) on synthetic datasets with varying proportions of linear and nonlinear relationships. GOLEM performs well only when the linear ratio is high, while SCORE performs well only when the nonlinear ratio is high. CaPS shows consistent performance across different linear ratios, demonstrating its ability to handle both linear and nonlinear relationships effectively.
read the caption
Figure 1: Performance of different solutions under datasets with different linear proportions. Since we don't know whether the real data is linear or nonlinear, it is difficult to choose an effective model. Thus, we need a method that works well in both linear and nonlinear and most possibly mixed cases.
🔼 This figure compares the performance of three causal discovery methods (GOLEM, SCORE, and CaPS) on synthetic datasets with varying proportions of linear and nonlinear relationships. GOLEM, designed for linear relationships, performs poorly when the linear ratio is low. SCORE, designed for nonlinear relationships, performs poorly when the linear ratio is high. CaPS, the proposed method in the paper, demonstrates robust performance across a wide range of linear proportions, highlighting its ability to handle datasets with mixed linear and nonlinear relationships.
read the caption
Figure 1: Performance of different solutions under datasets with different linear proportions. Since we don't know whether the real data is linear or nonlinear, it is difficult to choose an effective model. Thus, we need a method that works well in both linear and nonlinear and most possibly mixed cases.

🔼 The figure presents the performance comparison of CaPS and other state-of-the-art causal discovery methods on synthetic datasets SynER1 and SynER4. SynER1 represents sparser graphs, while SynER4 represents denser graphs. The x-axis shows the linear proportion in the datasets, ranging from 0.0 (all nonlinear) to 1.0 (all linear). The y-axis shows the performance metrics, namely SHD (Structural Hamming Distance), SID (Structural Intervention Distance), and F1 score. Lower SHD and SID values indicate better performance. Higher F1 scores indicate better performance. The figure illustrates how CaPS performs well across various linear proportions, outperforming other methods, especially in scenarios with mixed linear and nonlinear relations.
read the caption
Figure 2: Results of SynER1 and SynER4 with different linear proportions, where linear proportion equal to 0.0 means all relations are nonlinear and 1.0 means all relations are linear.

🔼 This figure displays the performance of various causal discovery methods on synthetic datasets (SynER1 and SynER4) with varying proportions of linear and nonlinear relationships. The x-axis represents the proportion of linear relationships, ranging from 0 (completely nonlinear) to 1 (completely linear). The y-axis shows the performance metrics SHD, SID, and F1 score. The figure illustrates how the performance of different methods changes as the ratio of linear to nonlinear relationships varies, highlighting the effectiveness of CaPS in handling both types of relationships well.
read the caption
Figure 2: Results of SynER1 and SynER4 with different linear proportions, where linear proportion equal to 0.0 means all relations are nonlinear and 1.0 means all relations are linear.
More on tables

🔼 This table presents the results of applying various causal discovery methods, including those based on acyclicity constraints and ordering-based approaches, to two real-world datasets: Sachs and Syntren. The metrics used to evaluate the performance of each method are the structural Hamming distance (SHD), the structural intervention distance (SID), and the F1 score. Lower SHD and SID values indicate better performance, while a higher F1 score signifies improved accuracy. The table allows for a comparison of the performance of CaPS against existing methods on real-world data, highlighting its strengths and weaknesses in different scenarios.
read the caption
Table 1: Results of real-world datasets, including three methods based on acyclicity constraint and five ordering-based methods. More baselines are given in Appendix C.4.

🔼 This table presents the results of applying various causal discovery methods on two real-world datasets: Sachs and Syntren. It compares the performance of CaPS against other state-of-the-art methods in terms of three metrics: Structural Hamming Distance (SHD), Structural Intervention Distance (SID), and F1 score. Lower SHD and SID values indicate better performance, while a higher F1 score represents better performance. The table also includes ablation studies for CaPS, showing the impact of key components of the method (Theorem 1 and parent score).
read the caption
Table 1: Results of real-world datasets, including three methods based on acyclicity constraint and five ordering-based methods. More baselines are given in Appendix C.4.
Full paper#