↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Existing research on Sharpness-Aware Minimization (SAM) mainly focuses on the sharpness metric near local minima, neglecting crucial aspects like early convergence and behavior with data anomalies. This creates limitations in understanding SAM’s effectiveness, particularly in non-convex scenarios and when dealing with scale-invariant problems common in deep learning architectures like LoRA. These limitations hinder the development of computationally efficient SAM variants for large-scale applications.
This paper introduces ‘balancedness’, a new metric, to analyze SAM’s global behavior, thereby addressing the above issues. The authors theoretically and empirically demonstrate that SAM promotes balancedness, and this regularization is data-responsive, impacting outliers more strongly. They leverage these insights to develop BAR, a resource-efficient SAM variant, which substantially improves test performance and saves over 95% of SAM’s computational overhead across various finetuning tasks on different language models. BAR represents a significant step towards making SAM more practical and scalable for large-scale deep learning applications.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in deep learning optimization and generalization. It introduces a novel perspective on Sharpness-Aware Minimization (SAM), addressing limitations in existing theoretical understanding. The proposed BAR algorithm offers a significant computational advantage, making SAM applicable to larger models, a major hurdle in current research. Furthermore, the study opens new avenues for investigating implicit regularization and its connection to data anomalies.
Visual Insights#

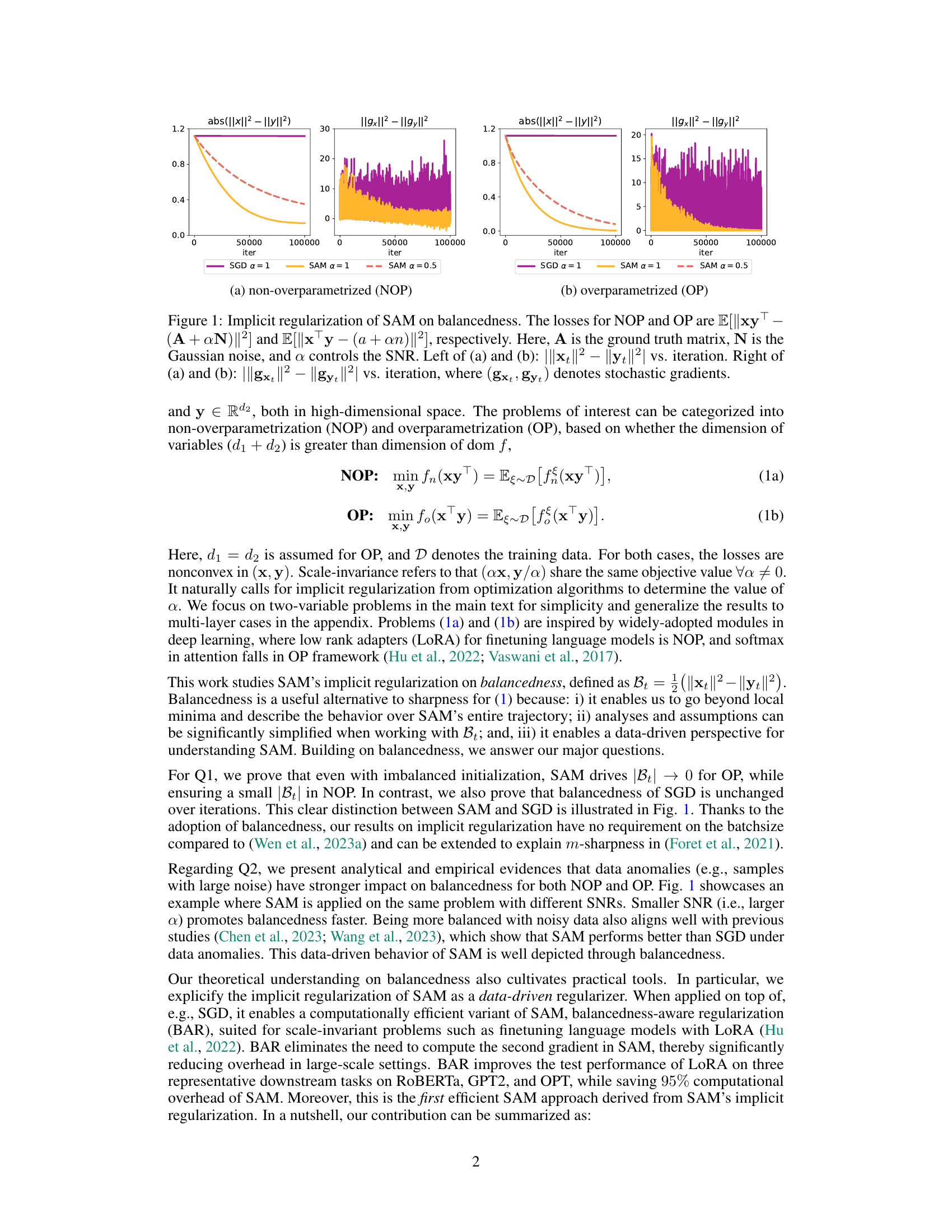
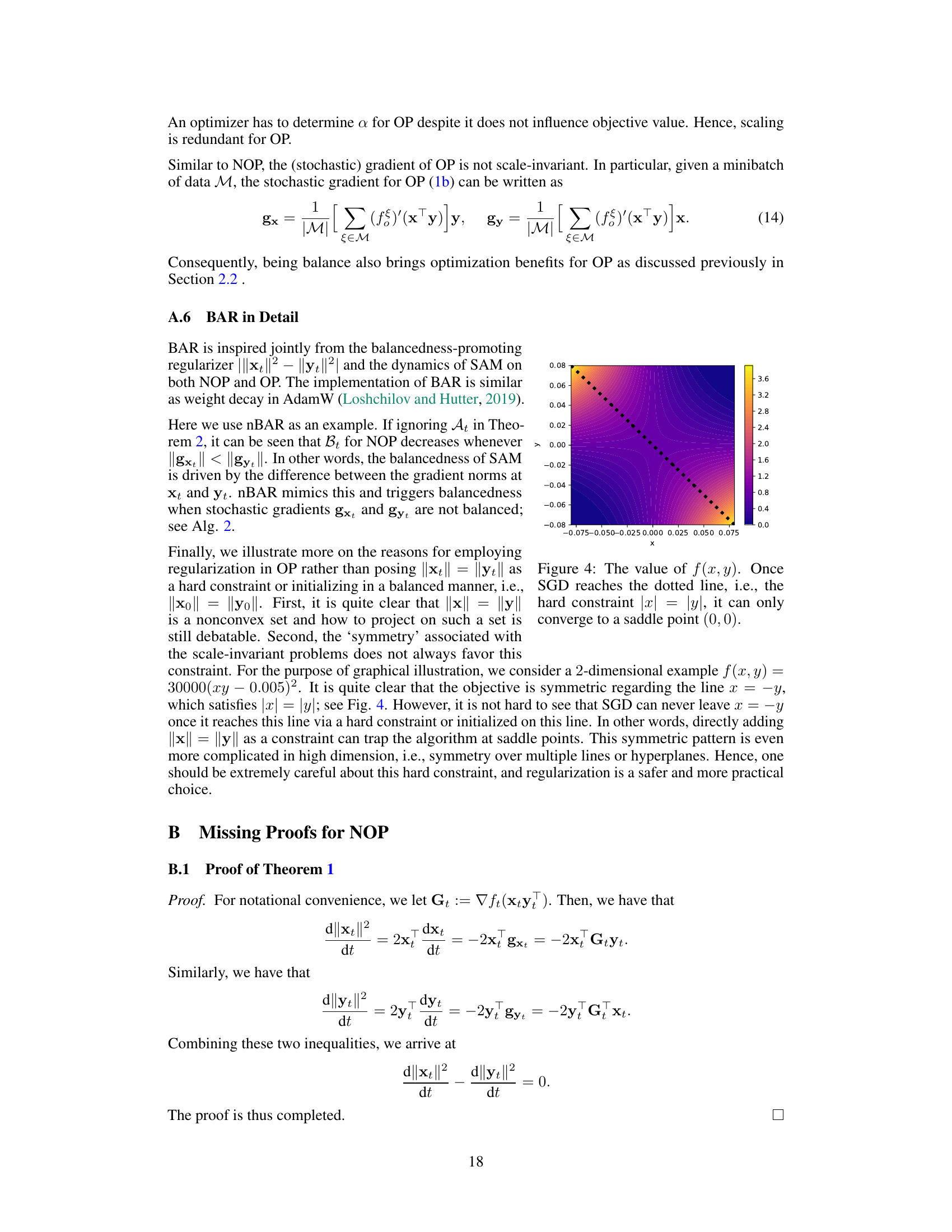
This figure demonstrates the implicit regularization of Sharpness-Aware Minimization (SAM) on balancedness, a new metric introduced in the paper. It shows the absolute difference between the squared norms of two variables (||xt||² - ||yt||²) and the difference between their gradient norms (||gxt||² - ||gyt||²) over training iterations for both non-overparametrized (NOP) and overparametrized (OP) problems. Different signal-to-noise ratios (SNR) are also tested. The results illustrate that SAM promotes balancedness (the difference approaches zero) while SGD does not, and this regularization effect is stronger when there are data anomalies (low SNR).

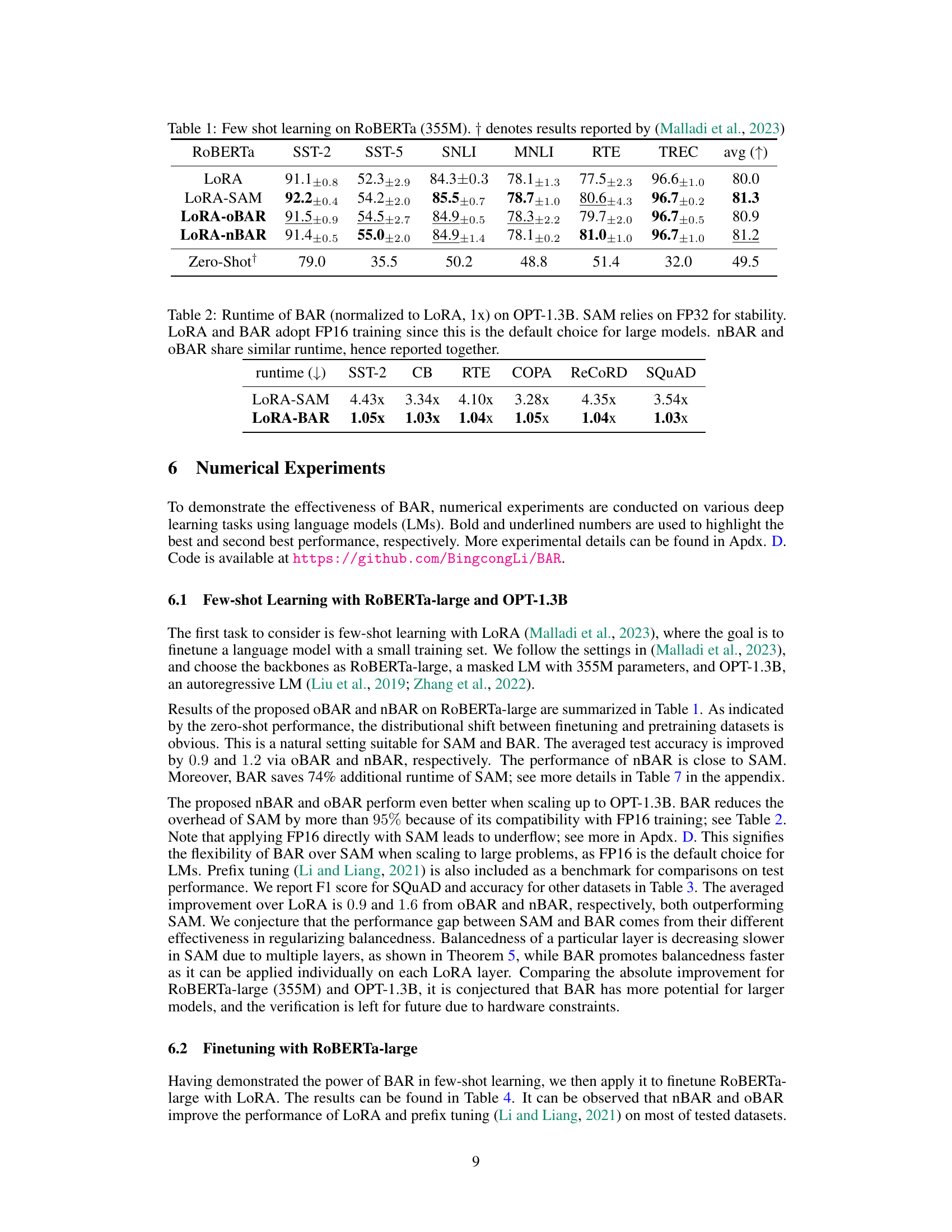
This table presents the results of few-shot learning experiments conducted on the RoBERTa-large language model (355M parameters). It compares the performance of LoRA (Low-Rank Adaptation), LoRA combined with SAM (Sharpness-Aware Minimization), and LoRA combined with the proposed BAR (Balancedness-Aware Regularization) methods. The results are shown for several downstream tasks (RTE, SST-2, SST-5, SNLI, MNLI, and TREC), with the average performance across tasks also provided. The ‘Zero-Shot’ row shows the performance without any fine-tuning, serving as a baseline.
In-depth insights#
SAM’s Implicit IR#
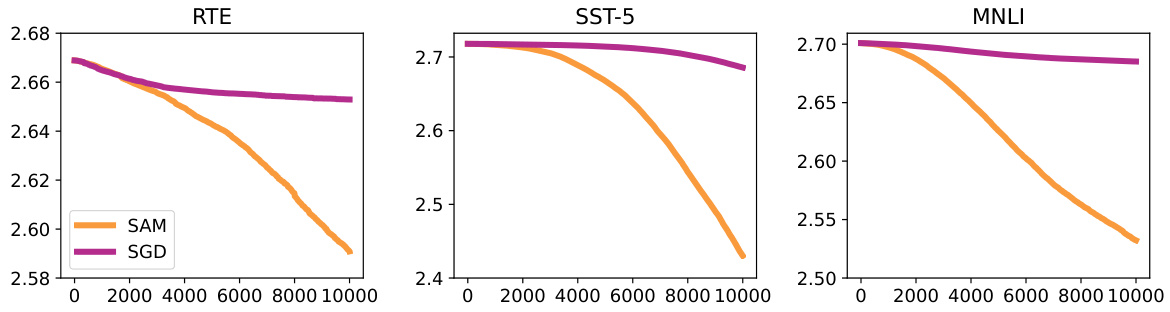
The core idea behind the paper is to explore the implicit regularization of Sharpness Aware Minimization (SAM). SAM’s implicit regularization (IR) is not well understood, especially regarding its global behavior and response to data anomalies. The authors introduce the concept of ‘balancedness’—the difference between the squared norms of two variable groups—to better capture SAM’s global dynamics. They show that SAM implicitly promotes balancedness, and this effect is data-dependent, with outliers exerting stronger influence. This observation aligns with the empirical success of SAM in handling outliers better than SGD. Leveraging this IR, the authors develop a computationally efficient variant of SAM called Balancedness-Aware Regularization (BAR), which achieves significant computational savings while maintaining or improving performance. The key contribution lies in explicating SAM’s IR through the lens of ‘balancedness’, leading to both theoretical understanding and practical improvements in model finetuning.
Balancedness Metric#
The paper introduces a novel metric called “balancedness” to analyze the implicit regularization in Sharpness-Aware Minimization (SAM). Unlike sharpness, which focuses on the local curvature around minima, balancedness measures the difference between the squared norms of two variable groups, offering a more global perspective on SAM’s behavior. This is particularly useful for scale-invariant problems, where the scale of variables doesn’t impact the objective function. The authors demonstrate that SAM implicitly promotes balancedness, and this regularization is data-responsive, meaning outliers have a stronger effect. This insight leads to a more efficient SAM variant, BAR, that directly regularizes balancedness, offering significant computational savings. Balancedness provides a richer understanding of SAM’s generalization capabilities than sharpness alone, especially in scenarios with data anomalies, and its introduction is a significant contribution of this work.
BAR: Efficient SAM#
The heading ‘BAR: Efficient SAM’ suggests a novel optimization algorithm, BAR, designed to improve the efficiency of Sharpness-Aware Minimization (SAM). BAR likely addresses SAM’s computational cost, a significant limitation hindering its broader application, particularly in large-scale models. The efficiency gains are likely achieved by leveraging the implicit regularization properties of SAM, specifically focusing on a new metric like ‘balancedness’ instead of directly optimizing sharpness. This strategic shift allows BAR to potentially reduce the computational overhead associated with second-order derivative calculations within SAM. The effectiveness of BAR would ideally be demonstrated through empirical results showcasing improved performance on benchmark tasks while significantly reducing training time compared to standard SAM. The development of BAR is a valuable contribution to the field, making the benefits of SAM more accessible for a wider range of applications. Further investigation into the precise mechanisms of BAR’s efficiency and its performance across diverse model architectures and datasets would provide deeper insights.
Scale-Invariant Focus#
A scale-invariant focus in a research paper would likely explore the impact of scaling on model performance and generalization. This often involves examining how the model behaves when input data or model parameters are multiplied by a scalar value. Key aspects might include analyzing the model’s sensitivity to scaling, exploring theoretical guarantees of scale invariance (if applicable), and demonstrating that performance is not significantly affected by such changes. The work could potentially introduce new techniques for designing or training scale-invariant models, leading to improved robustness and generalization. A key advantage is the potential for enhanced model transferability and adaptability to various datasets or domains. A significant challenge lies in mathematically characterizing and proving scale invariance, especially for complex models like deep neural networks. The paper might compare different optimization strategies under scaled conditions, providing valuable insights into the impact of scaling on optimization behavior and convergence.
Future Work: LoRA+#
The heading ‘Future Work: LoRA+’ suggests exploring extensions and improvements to the Low-Rank Adaptation (LoRA) technique. This could involve research into optimizing LoRA for various architectures beyond language models, such as computer vision or time-series data. Another avenue would be developing more efficient LoRA variants, potentially through advanced matrix factorization methods or exploring different low-rank approximation strategies. Addressing the limitations of LoRA concerning data anomalies and distributional shifts would also be crucial. This involves investigating how LoRA interacts with imbalanced or noisy data and devising strategies to mitigate this interaction. Finally, a formal theoretical analysis of LoRA+’s implicit regularization properties could provide deeper understanding and inform the design of future improvements. This could involve linking the properties of LoRA+ to concepts like sharpness or balancedness to improve its generalization capabilities.
More visual insights#
More on figures
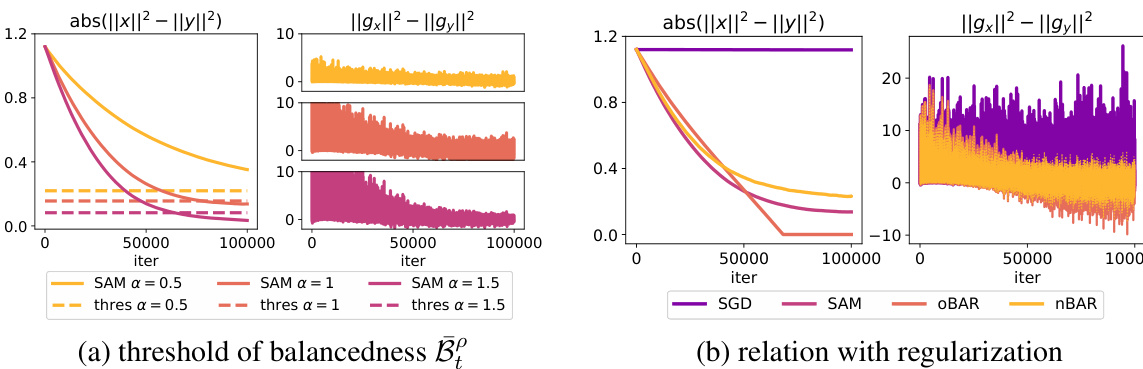
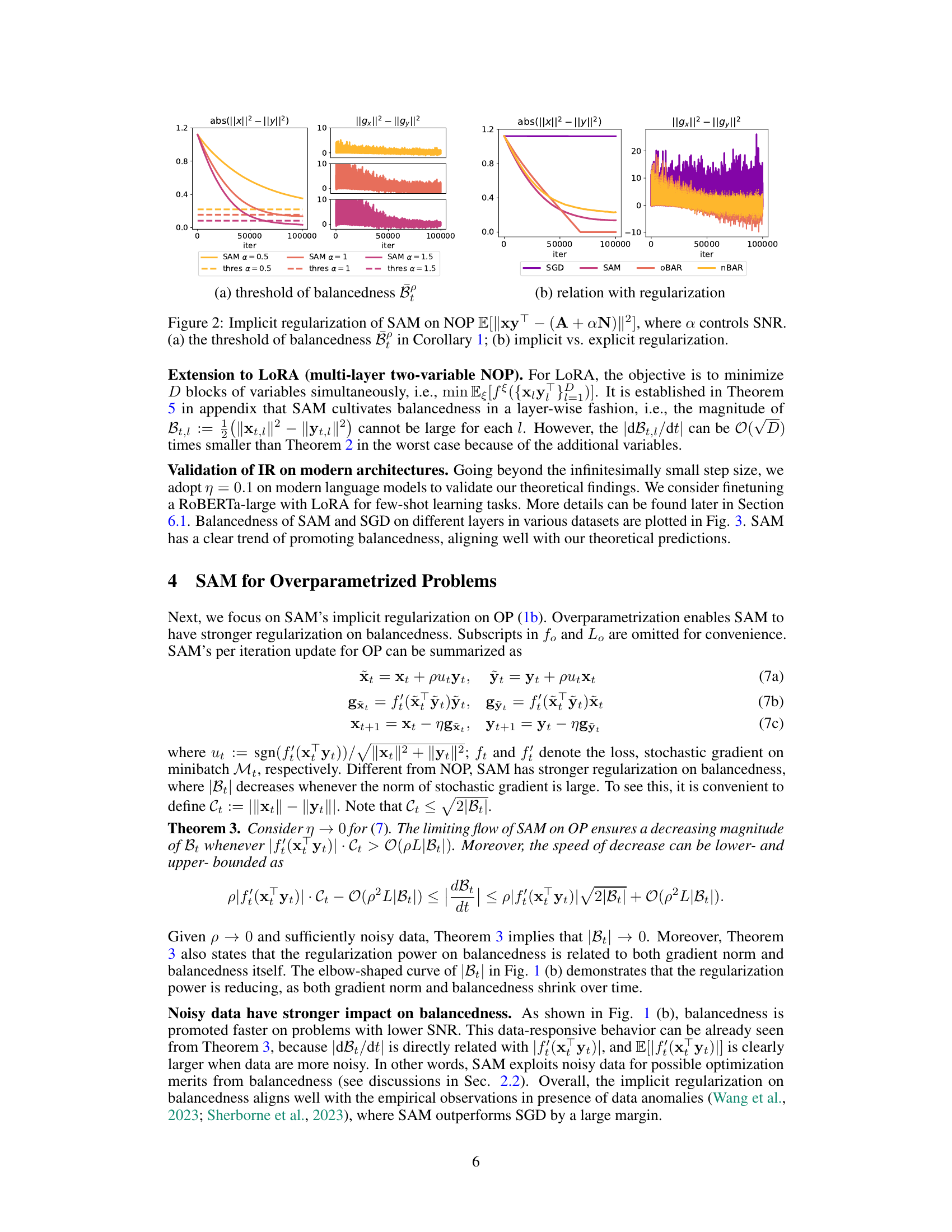
This figure illustrates the implicit regularization of Sharpness Aware Minimization (SAM) on balancedness for non-overparametrized problems. Panel (a) shows how the absolute difference between the squared norms of two variables (balancedness) changes over iterations for SAM and a thresholded version of SAM at different signal-to-noise ratios (SNR). The right side of (a) depicts the difference between the squared norms of the gradients of the two variables. Panel (b) compares the performance of SAM, SGD, and two proposed variants (OBAR, nBAR) that explicitly incorporate balancedness, again showing how the balancedness changes with iterations. In both cases, it is shown that SAM promotes balancedness, and that this effect is stronger in the presence of noise (lower SNR).
This figure demonstrates the implicit regularization of Sharpness-Aware Minimization (SAM) on balancedness, which is defined as the difference between the squared norms of two variables (x and y). The left panels show the absolute difference between the norms of x and y over training iterations for non-overparametrized (NOP) and overparametrized (OP) scenarios. The right panels display the corresponding difference in the norms of their gradients. The results illustrate that SAM promotes balancedness (the difference in norms approaches zero), and this effect is stronger when the signal-to-noise ratio (SNR) is lower (more noise).

This figure shows the implicit regularization of Sharpness Aware Minimization (SAM) on balancedness for both non-overparametrized (NOP) and overparametrized (OP) problems. The plots show the absolute difference between the squared norms of two variables (||xt||² - ||yt||²) and the difference between the squared norms of their gradients (|||gxt||² - ||gyt||²) over training iterations. Different subplots show the effect of varying signal-to-noise ratio (SNR). The results show that SAM promotes balancedness (i.e. equal norms), and this regularization is stronger for data with lower SNR.
More on tables

This table presents the results of few-shot learning experiments conducted using a RoBERTa-large language model (355M parameters). It compares the performance of different approaches: LoRA (Low-Rank Adaptation), LoRA combined with SAM (Sharpness-Aware Minimization), LoRA with oBAR (Overparametrized Balancedness-Aware Regularization), and LoRA with nBAR (Non-Overparametrized Balancedness-Aware Regularization). The results are shown for various downstream tasks (RTE, SST-2, SST-5, SNLI, MNLI, and TREC) and are reported as average accuracy with standard deviation. A zero-shot baseline is included for reference.
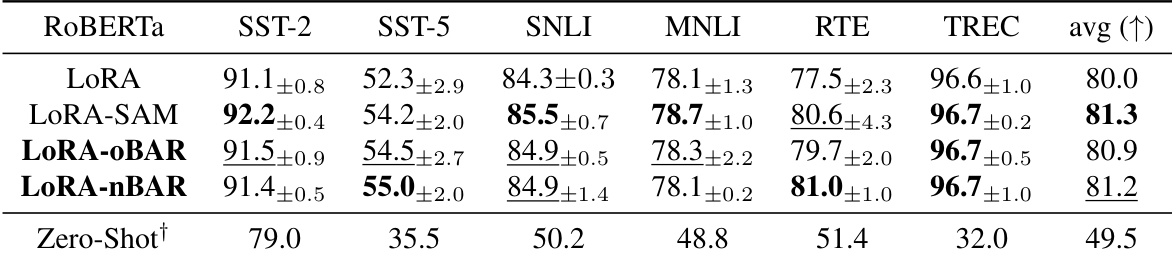
This table presents the results of few-shot learning experiments using the RoBERTa-large language model. The results compare the performance of LoRA (Low-Rank Adaptation) with three variations: LoRA-SAM (Sharpness-Aware Minimization), LoRA-oBAR (Overparametrized Balancedness-Aware Regularization), and LoRA-nBAR (Non-Overparametrized Balancedness-Aware Regularization). The table shows the average accuracy achieved on seven different downstream tasks (RTE, SST-2, SST-5, SNLI, MNLI, RTE, TREC), along with the zero-shot performance (without any fine-tuning) for comparison. The results demonstrate the effectiveness of BAR in achieving comparable or better performance than SAM while significantly reducing computational overhead.

This table shows the runtime of Balancedness-Aware Regularization (BAR) compared to LoRA and SAM on the OPT-1.3B model. The runtime is normalized relative to LoRA, with 1x representing the runtime of LoRA. The table highlights that BAR is significantly faster than SAM, while maintaining similar performance. The use of FP16 precision for LORA and BAR contributes to their speed advantage over SAM, which uses FP32 for stability reasons.
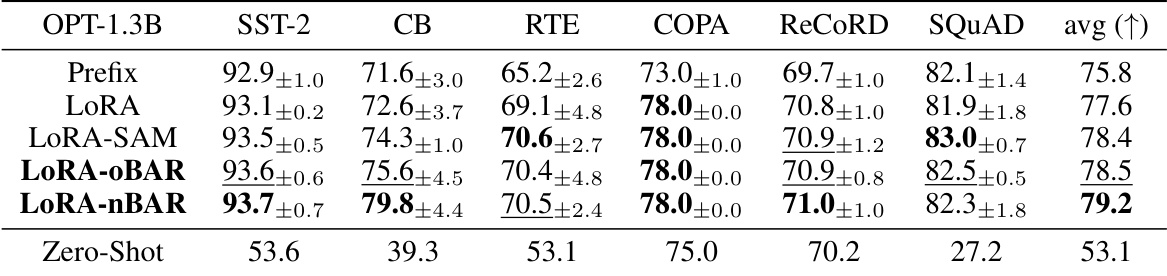
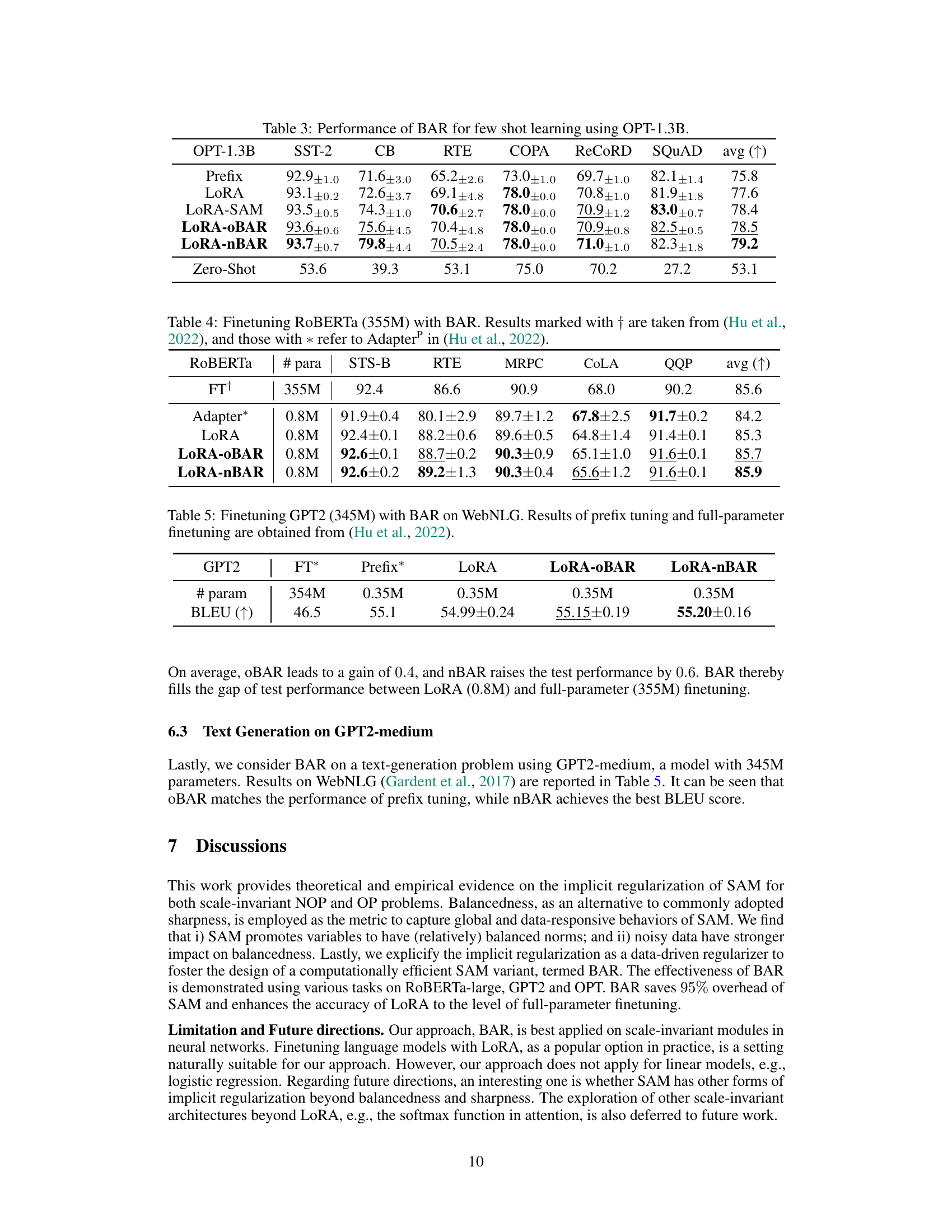
This table presents the results of few-shot learning experiments using the OPT-1.3B language model. The performance of LoRA (Low-Rank Adaptation), LoRA with SAM (Sharpness-Aware Minimization), LoRA with oBAR (Overparametrized Balancedness-Aware Regularization), and LoRA with nBAR (Non-Overparametrized Balancedness-Aware Regularization) are compared. The results are shown for several datasets (SST-2, CB, RTE, COPA, ReCoRD, and SQUAD), along with a zero-shot baseline. The average performance across all datasets is also given. The table highlights the improved performance of BAR compared to LoRA and LoRA with SAM, demonstrating BAR’s effectiveness in few-shot learning scenarios.
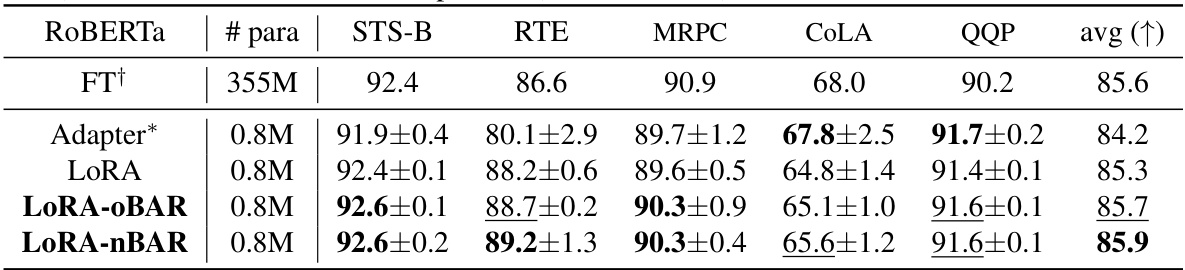
This table shows the results of finetuning a RoBERTa-large language model (355M parameters) using different methods: full finetuning (FT+), Adapter, LoRA, LoRA with OBAR, and LoRA with nBAR. The results are presented for several downstream tasks (STS-B, RTE, MRPC, CoLA, QQP) and an average score across all tasks. The table demonstrates the performance improvement of the proposed balancedness-aware regularization (BAR) methods compared to standard LoRA and other baselines.

This table shows the BLEU scores achieved by different methods for text generation on the WebNLG dataset using the GPT2-medium language model. It compares the performance of full fine-tuning (FT), prefix tuning, LoRA, LoRA with OBAR, and LoRA with nBAR. The results highlight the improved performance of LoRA when combined with BAR compared to standard LoRA and other methods.
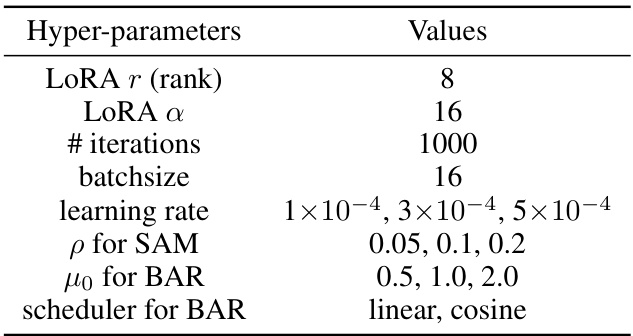
This table shows the hyperparameter settings used for few-shot learning experiments with the RoBERTa-large model. It lists the values tested for several key hyperparameters, including LoRA rank, LoRA alpha, number of training iterations, batch size, learning rate, sharpness parameter (p) for SAM, and the mu0 and scheduler values for BAR.
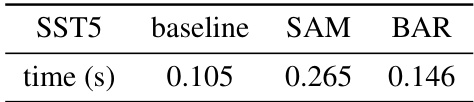
This table shows the per-iteration runtime for training a RoBERTa-large model on the SST5 dataset using three different optimization methods: a baseline method, Sharpness-Aware Minimization (SAM), and Balancedness-Aware Regularization (BAR). The results demonstrate the computational efficiency of BAR compared to SAM, while maintaining comparable performance.

This table shows the hyperparameters used for few-shot learning experiments with the RoBERTa-large model. The hyperparameters include the rank and scaling factor for LoRA, the number of training iterations, batch size, learning rate for the optimizer, the radius parameter (ρ) for SAM, the regularization coefficient (μ0) for BAR, and the scheduling strategy used for BAR (linear or cosine). These settings were likely tuned to optimize the performance of the model on the specific tasks.

This table compares the per-iteration runtime of three different optimization methods: baseline, SAM, and BAR, when fine-tuning the OPT-1.3B model on the RTE dataset. It highlights the significant reduction in runtime achieved by BAR compared to SAM while maintaining comparable precision using FP16.
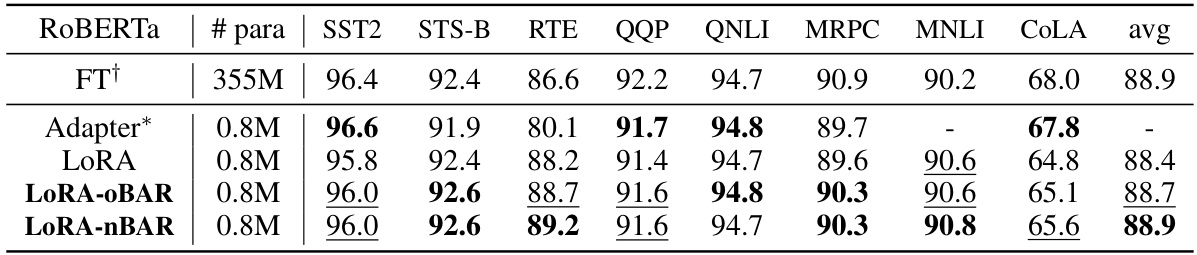
This table shows the results of finetuning a RoBERTa-large language model (355M parameters) using three different methods: LoRA, LoRA-OBAR, and LoRA-nBAR. The performance is evaluated on several downstream tasks, including STS-B, RTE, MRPC, MNLI, COLA, and QQP. The results are compared against a full finetuning approach (FT) and an Adapter-based approach. The table highlights the improved accuracy achieved by the proposed balancedness-aware regularization (BAR) methods while maintaining comparable efficiency to LoRA.

This table presents the results of applying Balancedness-Aware Regularization (BAR) to few-shot learning tasks using the OPT-1.3B language model. It compares the performance of BAR against LoRA (a low-rank adaptation technique), LoRA combined with SAM (Sharpness-Aware Minimization), and a zero-shot baseline. The results are shown for several different datasets and metrics, demonstrating the improvement in performance achieved by BAR.
Full paper#