Improved Guarantees for Fully Dynamic $k$-Center Clustering with Outliers in General Metric Spaces

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on dynamic clustering algorithms and handling outliers. It provides significant improvements over existing methods and opens up new avenues for research in handling continuous data updates efficiently. The general metric space applicability broadens its potential use in various data-intensive fields.

Visual Insights

#

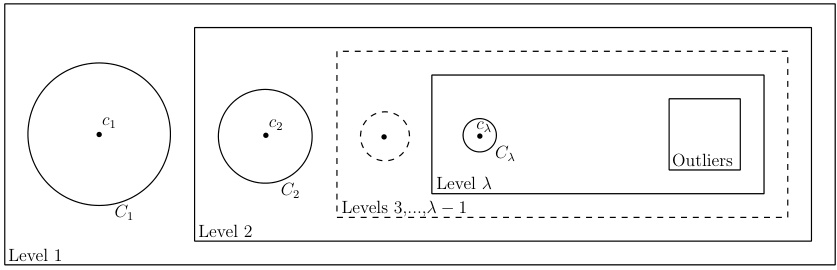
This figure illustrates the hierarchical structure of clusters generated by the offline k-center clustering algorithm with outliers. Each level represents a cluster, where the first λ levels (λ ≤ k) correspond to the k clusters found by the algorithm, and the final level represents the outliers. Level 1 contains the points closest to the first center chosen; level 2 contains the remaining points close to the second center, and so on. The algorithm iteratively constructs these levels until k clusters are found or no more points remain to be assigned. The outermost dashed box represents the entire dataset.

This table visually represents the output of the offline k-center clustering algorithm with outliers. Each of the first λ levels represents a cluster, where λ is less than or equal to k. Each cluster is a ball of radius 4r centered at a point c_i. The last level (λ+1) represents the outliers, i.e., the points that are not covered by any of the first λ clusters. The algorithm iteratively builds these levels, creating a hierarchical structure.

In-depth insights

#

Dynamic k-Center

#

Dynamic k-center clustering tackles the challenge of efficiently maintaining a k-center clustering solution as the underlying dataset undergoes continuous updates (insertions and deletions). This contrasts with the static k-center problem, which operates on a fixed dataset. The dynamic variant is crucial for real-world applications where data streams constantly change. Efficient update time is a key concern in dynamic k-center, requiring algorithms that can quickly adapt to changes without recomputing the entire solution from scratch. Approximation algorithms are often employed because finding optimal solutions in dynamic settings is computationally expensive. Approximation guarantees ensure the solution’s quality relative to the optimal solution, even with the dataset’s constant evolution. Further complicating the problem is the introduction of outliers, data points deviating significantly from the overall structure. Handling outliers requires algorithms that can effectively identify and exclude them, while maintaining the desired clustering quality. General metric spaces pose another significant challenge, demanding algorithms not reliant on specific distance function properties (unlike Euclidean space). This necessitates more sophisticated techniques to maintain approximate solutions efficiently in diverse data contexts.

Outlier Robustness

#

Outlier robustness is a critical aspect of clustering algorithms, especially when dealing with real-world datasets often containing noisy or irrelevant data points. The paper addresses this by exploring the k-center clustering problem with outliers, a model that explicitly allows for the exclusion of a certain number of points from the clustering process. The key challenge lies in balancing the need to achieve accurate clustering of the core data with the efficiency and effectiveness of handling the outliers. The proposed algorithm uses sampling-based techniques to identify potential outliers, ensuring that the core clustering remains unaffected by these noisy points. This approach provides strong theoretical guarantees of approximation quality. However, a deeper analysis is needed to understand the algorithm’s behavior and limitations under various outlier distributions and data characteristics. Furthermore, the algorithm’s scalability and efficiency should be examined in the context of large-scale datasets, where the computational cost of outlier detection could significantly impact performance. Finally, the impact of parameter choices such as the number of outliers allowed and the approximation factor on the algorithm’s output needs to be thoroughly evaluated. Practical experimentation across various real-world datasets is crucial to validate its effectiveness and robustness in diverse settings.

General Metric Space

#

The concept of “General Metric Space” in the context of k-center clustering with outliers is crucial because it extends the applicability of the algorithm beyond specific metric spaces like Euclidean space or those with bounded doubling dimension. Many real-world datasets don’t conform to these restrictive assumptions. A general metric space algorithm offers greater flexibility and broader applicability to diverse applications, such as those involving non-geometric data with custom distance functions. The key challenge addressed in such a context is the lack of structure inherent in general metric spaces, making the design and analysis of efficient algorithms considerably harder. The algorithm’s ability to provide approximation guarantees despite this lack of structure is a significant contribution, highlighting its practical relevance. Maintaining efficiency in the dynamic setting (insertions and deletions) for such a broad class of metric spaces presents additional significant theoretical challenges that are successfully overcome by this research.

Algorithm Analysis

#

The Algorithm Analysis section would critically assess the efficiency and effectiveness of the proposed dynamic k-center clustering algorithm. It would delve into the time complexity, focusing on both the amortized update time (per insertion or deletion) and any potential query times for retrieving the clustering solution. The analysis would need to rigorously justify the claimed O(e-3k6 log(k)log(Δ)) amortized update time, demonstrating how this bound is achieved across various scenarios, including the handling of outliers. Furthermore, the analysis should incorporate a discussion of the space complexity, detailing the data structures used and the memory requirements. A crucial aspect would be the approximation guarantees, proving the algorithm’s performance relative to the optimal (k, z)-center clustering solution. This might involve showing a (4+ε)-approximation ratio with high probability, along with a rigorous treatment of the outlier parameter (z) and its impact on approximation quality. The analysis would need to discuss any probabilistic components and justify the high probability claims. Finally, a comparative analysis, referencing existing dynamic k-center algorithms, would showcase the improvements and limitations of the novel approach.

Future Directions

#

Future research could explore several promising avenues. Extending the dynamic algorithm to handle more complex update operations, such as batch insertions or deletions, would enhance its practicality. Investigating the algorithm’s performance under various data distributions and metric space characteristics is crucial for a thorough understanding of its strengths and limitations. The current algorithm achieves a (4+ε) approximation; improving this approximation ratio, perhaps by refining the sampling techniques or data structure, is an open problem. A particularly interesting direction is adapting the algorithm for specific application domains, such as those with unique outlier characteristics or requiring fairness constraints. Finally, developing and empirically evaluating heuristics to improve the algorithm’s runtime could significantly enhance its performance in practical scenarios. These future directions would lead to a more robust and widely applicable fully dynamic k-center clustering algorithm.

More visual insights

#

More on figures

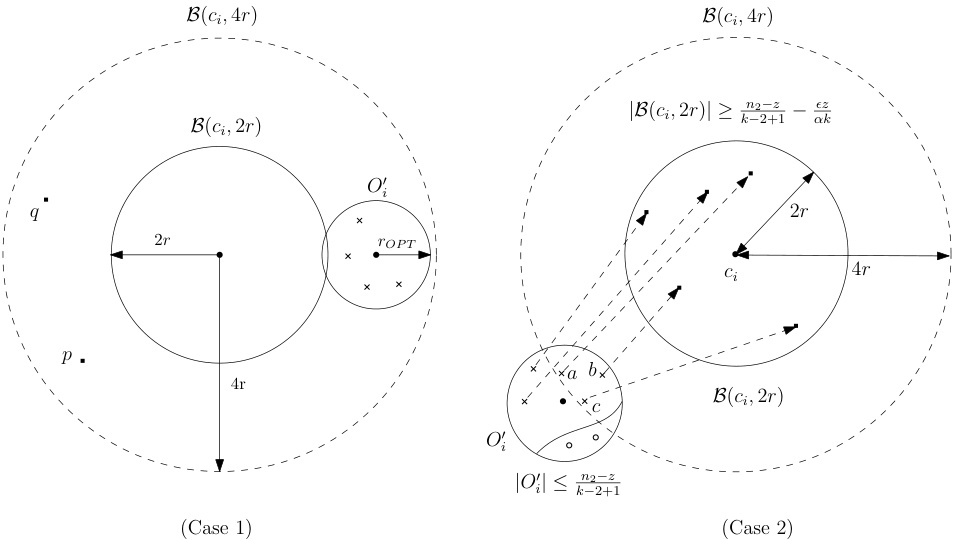
This figure illustrates two cases in the charging argument used to prove the approximation guarantee of the algorithm. Case 1 shows the situation where the ball B(ci, 2r) intersects a remaining modified optimal ball, allowing for a simple charging scheme. Case 2 addresses the scenario where B(ci, 2r) does not intersect any of the remaining modified optimal balls, requiring a more intricate charging argument and the introduction of artificial outliers.

This figure illustrates the hierarchical structure of the offline algorithm’s output. It shows how the algorithm creates a series of levels, each level representing a cluster obtained in an iteration. The first X levels represent the clusters found by the algorithm, while the last level (level λ+1) contains the remaining points that were not included in any cluster and are considered outliers. Each level uses a center and radius to define the cluster, and the clusters in higher levels only consider the points that remain after forming the clusters in lower levels. The process of iteratively constructing clusters and refining the sets of remaining points creates a hierarchical structure of levels reflecting the clustering result.

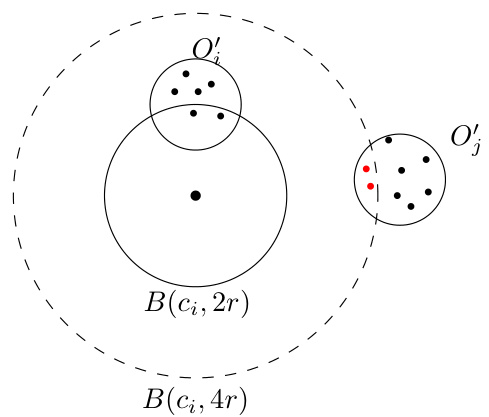
This figure illustrates the proof of a 6-approximation for the discrete version of the k-center problem with outliers. In the first part, before the deletion of the center cᵢ, cᵢ is used as the center of the cluster, and the cluster radius is 4r. After cᵢ is deleted, the second part shows that an arbitrary point p within a radius of 2r from the old center cᵢ can replace cᵢ as the new center. A cluster with p as its center and radius 6r can cover the same points that were originally covered by the cluster with center cᵢ and radius 4r.

More on tables

This table visually represents the output of the offline k-center clustering algorithm with outliers. It shows how the algorithm constructs at most k+1 levels. Each of the first k levels represents a cluster, while the last level (k+1) contains the outliers that are not covered by the k clusters. Each level i contains a cluster Ci, built iteratively in the i-th iteration of the algorithm. The algorithm stops either when k clusters have been created or when all points are clustered. The figure helps in understanding the hierarchical structure used in the fully dynamic algorithm.

This procedure handles both insertion and deletion of points. For each radius r in R, it checks if the current operation is an insertion or deletion. If it’s an insertion, it calls the INSERT procedure; otherwise, it calls the DELETE procedure. After updating the time, it checks for any postponed level constructions due to previous failures and triggers OFFLINECLUSTER if necessary.

Full paper

#