Accelerating Relative Entropy Coding with Space Partitioning

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it significantly accelerates relative entropy coding (REC), a crucial technique in neural compression, making it more practical for various applications. The proposed space partitioning method improves runtime and bitrate, broadening REC’s applicability and opening new avenues for research in efficient neural compression.

Visual Insights

#

This figure compares the standard REC algorithm with the proposed space partitioning approach. The standard approach involves a random search (red dots) to find samples aligning with the target distribution Q (green dot). The proposed method partitions the search space and reweights each partition, resulting in a more efficient search that reduces runtime by focusing on more relevant areas.

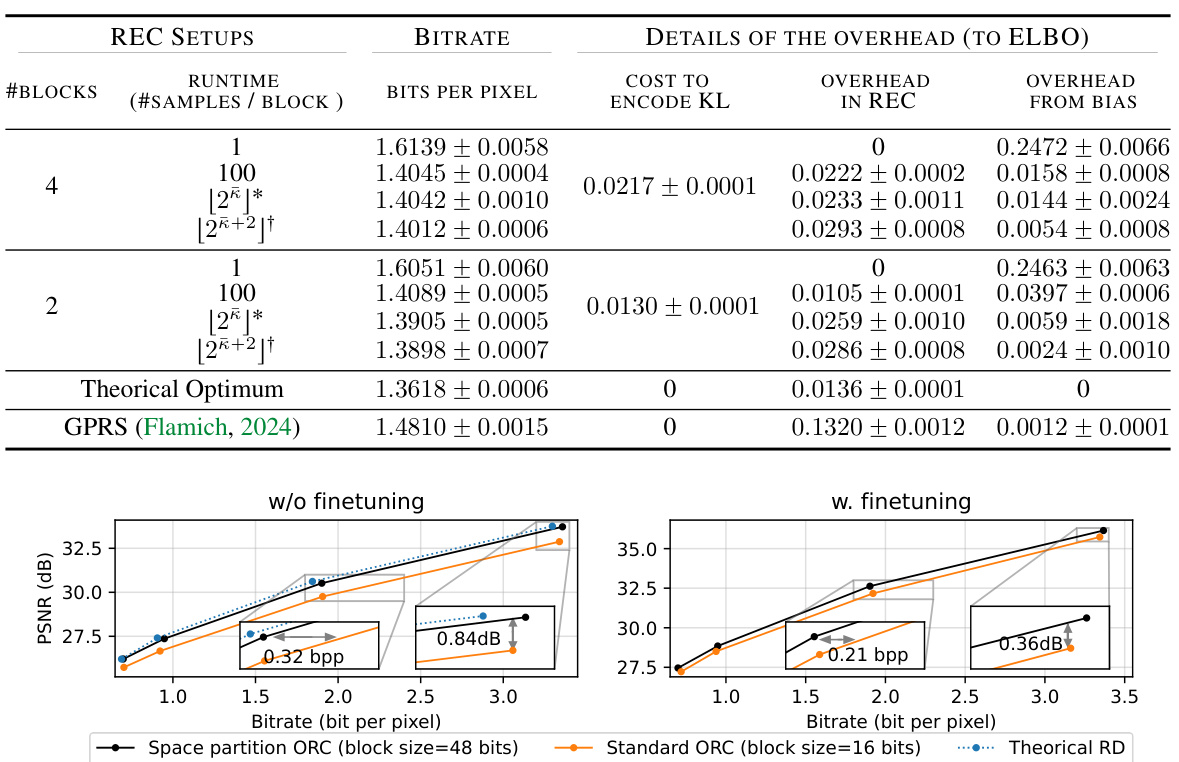
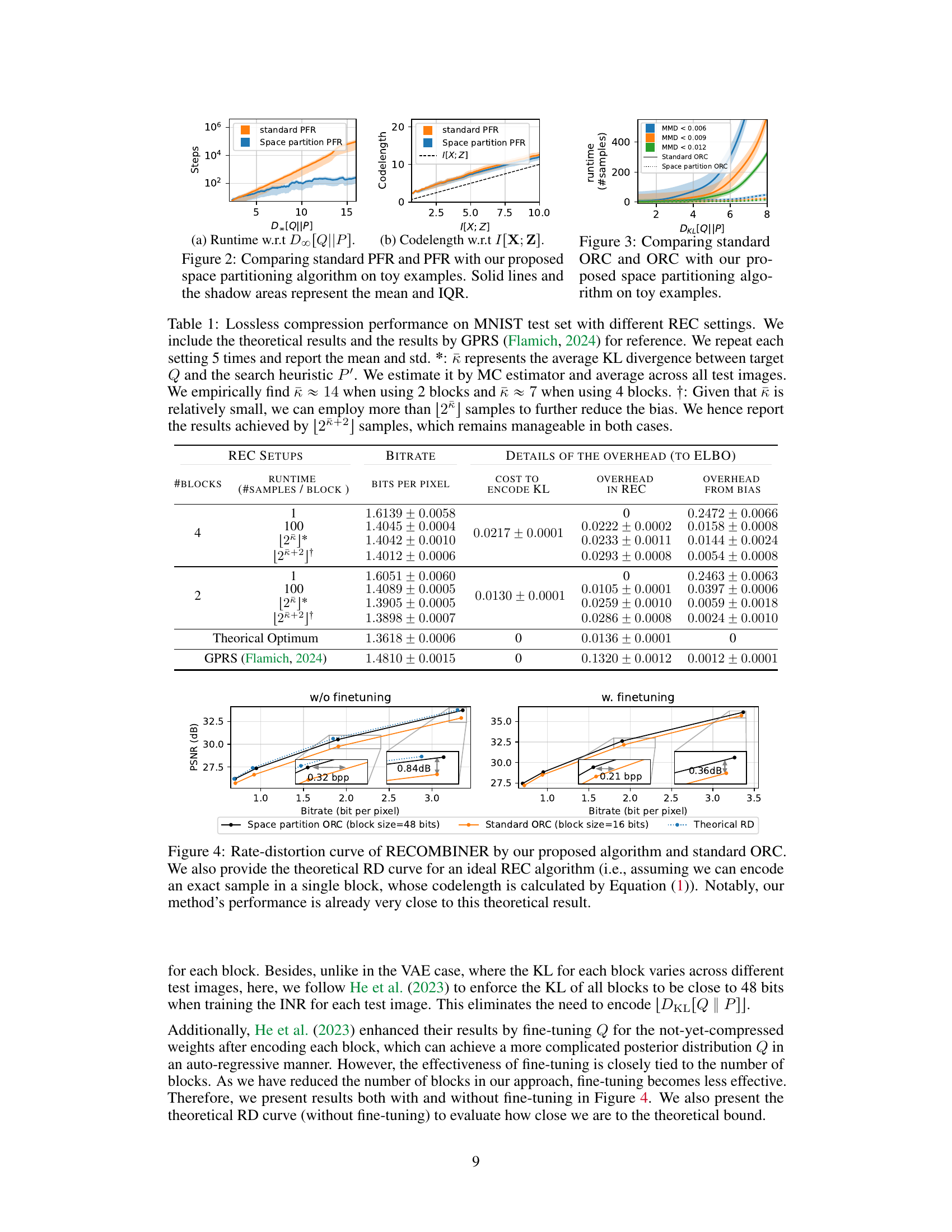
This table presents the results of lossless compression experiments on the MNIST dataset using different relative entropy coding (REC) settings. It compares the bitrate and runtime of the proposed space partitioning method against standard methods, including a theoretical optimum and GPRS. The table shows the impact of the number of blocks and samples per block on performance, and notes the estimation of KL divergence and resulting bias.

In-depth insights

#

REC Acceleration

#

The research paper explores methods for accelerating Relative Entropy Coding (REC), a technique used in neural compression. A key challenge with REC is its computationally expensive encoding process, which often scales exponentially with the KL divergence between the coding and target distributions. The paper addresses this by introducing a novel space-partitioning scheme. This approach strategically divides the encoding space into smaller regions, allowing for a more targeted and efficient search during encoding. Theoretical analysis demonstrates that this method maintains a near-optimal codelength while significantly reducing runtime. The effectiveness of this approach is empirically validated with experiments across synthetic datasets and real-world applications using VAEs and INRs, showing substantial improvements in compression efficiency, often exceeding previous methods. Space partitioning emerges as a crucial component in making REC more practical, particularly in high-dimensional scenarios where traditional methods become computationally prohibitive. However, the authors also acknowledge that their method’s efficiency depends on certain assumptions, particularly related to factorized mutual information, and there is room for future improvements by relaxing such restrictions.

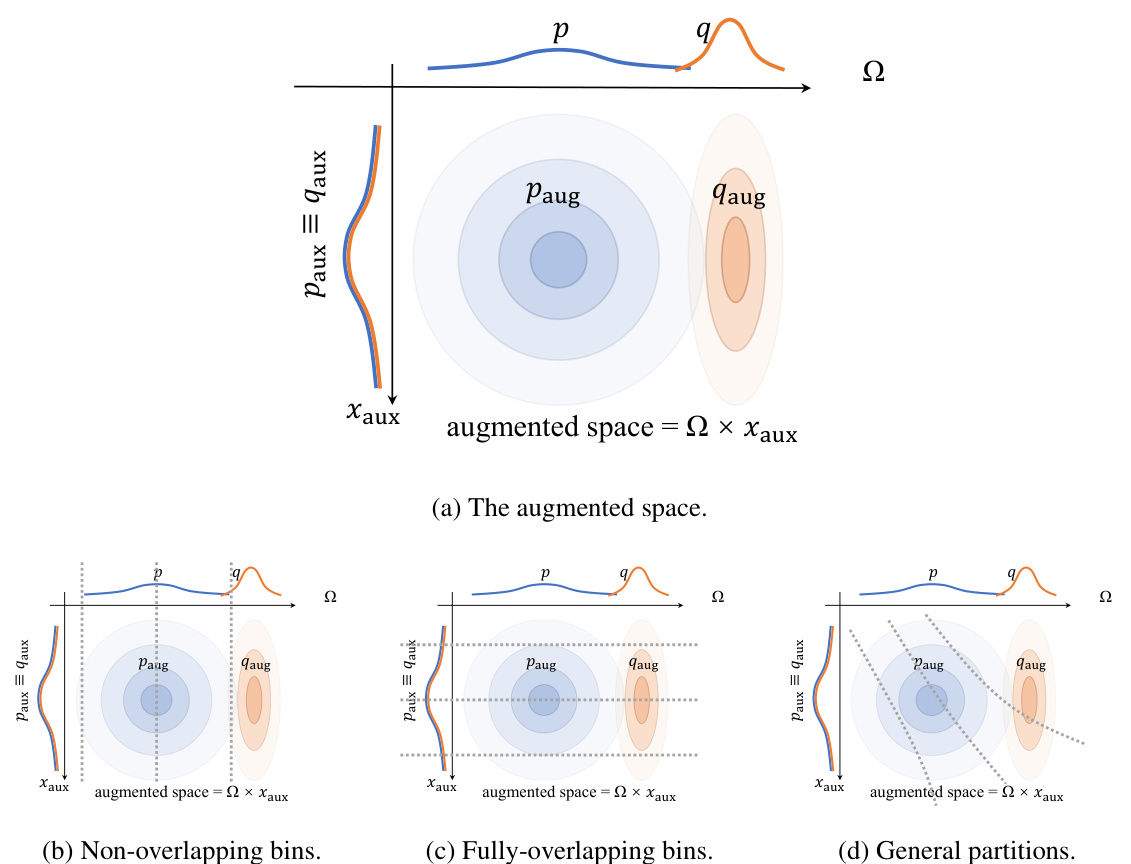
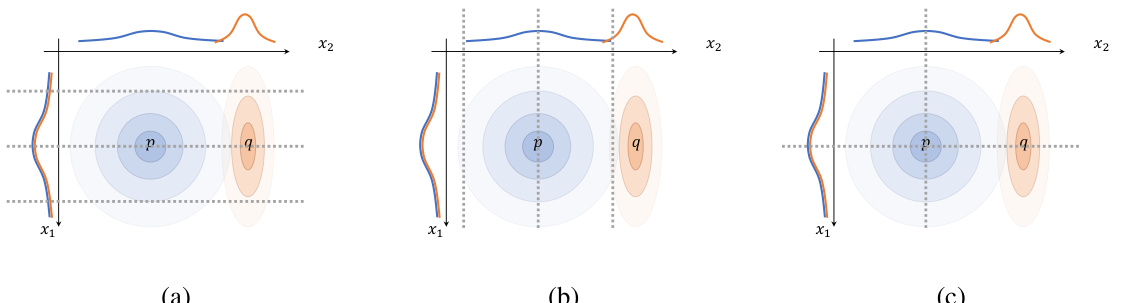
Space Partitioning

#

The core idea of “Space Partitioning” in this relative entropy coding (REC) acceleration method involves strategically dividing the continuous latent space into distinct regions or bins. This partitioning isn’t arbitrary; it’s guided by the target distribution (Q) and coding distribution (P). The goal is to create a search heuristic that prioritizes exploring regions where Q is most concentrated, thus reducing the computational cost associated with finding Q-distributed samples from P. This is achieved by reweighting the bins based on their relative importance under Q, making it more likely to sample from high-probability areas. The efficiency gain is evident in that fewer samples need to be drawn and evaluated to find a sufficiently close approximation. Different strategies for partitioning and weight assignment are explored, demonstrating flexibility in this approach, with the choice often influenced by the balance between computational efficiency and the desired accuracy of the final sample.

PFR/ORC Enhancements

#

The heading ‘PFR/ORC Enhancements’ suggests improvements to the Poisson Functional Representation (PFR) and Ordered Random Coding (ORC) algorithms, likely focusing on efficiency and practicality. PFR’s main drawback is its unpredictable runtime, making it unsuitable for real-time applications. ORC addresses this by introducing a fixed number of iterations, but this introduces bias. Therefore, improvements might involve novel search heuristics within the algorithms’ core processes or modifications to the underlying probability distributions to reduce the number of iterations needed for convergence. A focus on space partitioning is a likely strategy for achieving faster runtimes, possibly by prioritizing exploration of high-probability regions, which could dramatically reduce computation. Furthermore, managing the inherent trade-off between speed and bias in ORC is a crucial aspect of any enhancement, potentially involving adaptive methods to dynamically adjust the number of iterations based on the observed data characteristics. Finally, enhancements may include theoretical analysis demonstrating improved convergence rates or reduced bias compared to standard PFR/ORC, with experimental validation showcasing improved speed and/or accuracy on benchmark datasets.

Codelength Analysis

#

A rigorous codelength analysis is crucial for evaluating the efficiency of any compression scheme. In the context of relative entropy coding (REC), this involves carefully examining the number of bits required to encode a random sample from a target distribution, given a shared coding distribution between sender and receiver. The analysis should account for various factors, such as the Kullback-Leibler (KL) divergence between the distributions, dimensionality, and the computational cost of the encoding algorithm. A successful codelength analysis would demonstrate that the proposed REC method achieves a codelength that is close to the theoretical lower bound (e.g., mutual information), while maintaining reasonable computational efficiency. Bounds on the expected codelength, including extra costs due to space partitioning or search heuristics, would strengthen the analysis. Furthermore, a comparison of the proposed method’s codelength with existing REC techniques is necessary to showcase its relative improvement. Finally, the analysis should consider both the average and worst-case codelength scenarios, providing a comprehensive understanding of the algorithm’s performance under varying conditions. A thoughtful analysis would also include detailed proofs of theoretical claims and address potential limitations of the analysis itself, like assumptions made about the distribution, or the independence of samples.

Future of REC

#

The future of relative entropy coding (REC) hinges on addressing its current limitations, primarily the high computational cost. Research should focus on developing more efficient algorithms, potentially leveraging advanced search heuristics beyond space partitioning, or exploring alternative coding frameworks entirely. Combining REC with other compression techniques may yield synergistic benefits, leading to improved compression ratios and speed. Hardware acceleration through specialized processors or dedicated circuitry could dramatically improve REC’s performance. Furthermore, exploring the theoretical limits of REC and identifying novel applications in areas like lossless neural compression and high-dimensional data compression will be crucial. Finally, developing robust methods for handling non-factorized distributions and efficiently managing the overhead associated with side information is essential to expand REC’s practical applicability.

More visual insights

#

More on figures

This figure illustrates the difference between standard REC and REC with space partitioning. The standard REC algorithm randomly samples from the prior distribution P, often wasting time on samples that don’t contribute to finding a sample that matches the target distribution Q. The proposed space partitioning method divides the search space and adjusts the prior P to a new distribution P’, which is more closely aligned to Q. This results in faster encoding because fewer samples are needed to find a sample similar to the target distribution.

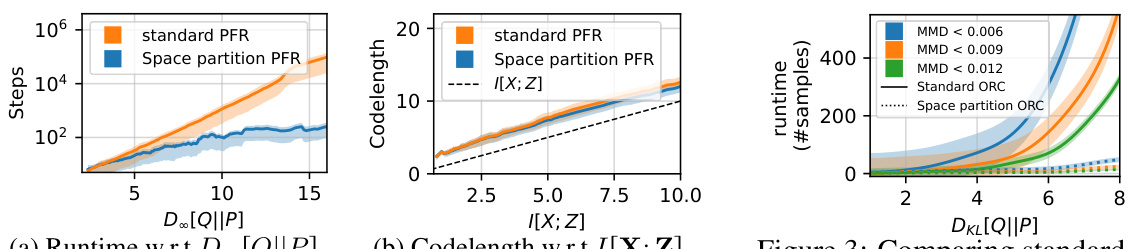
This figure compares the performance of the standard Poisson Functional Representation (PFR) algorithm with the proposed space-partitioning PFR algorithm on synthetic 5D Gaussian examples. The left panel shows the runtime (number of steps) versus the Rényi-∞ divergence between the target and coding distributions. The middle panel displays codelength versus mutual information. The right panel illustrates runtime versus Rényi-∞ divergence for approximate sampling, categorized by the maximum mean discrepancy (MMD) between the encoded samples and the target distribution. The plots demonstrate that the proposed space-partitioning approach significantly reduces runtime while maintaining comparable codelength in both exact and approximate sampling scenarios.

This figure illustrates the difference between standard REC and the proposed space partitioning REC. In standard REC, many samples are drawn from the prior distribution P before finding a sample aligning with target distribution Q. The proposed method partitions the space and adjusts the prior, which leads to more relevant samples and faster runtime.

This figure illustrates the difference between the standard REC algorithm and the proposed space partitioning method. The standard method randomly samples from the prior distribution P until a sample is found that is sufficiently close to the target distribution Q. The proposed method first partitions the space into smaller grids and then reweights the grids based on the target distribution. This results in the samples being drawn from a modified prior distribution that is better aligned with the target distribution, leading to faster encoding times.

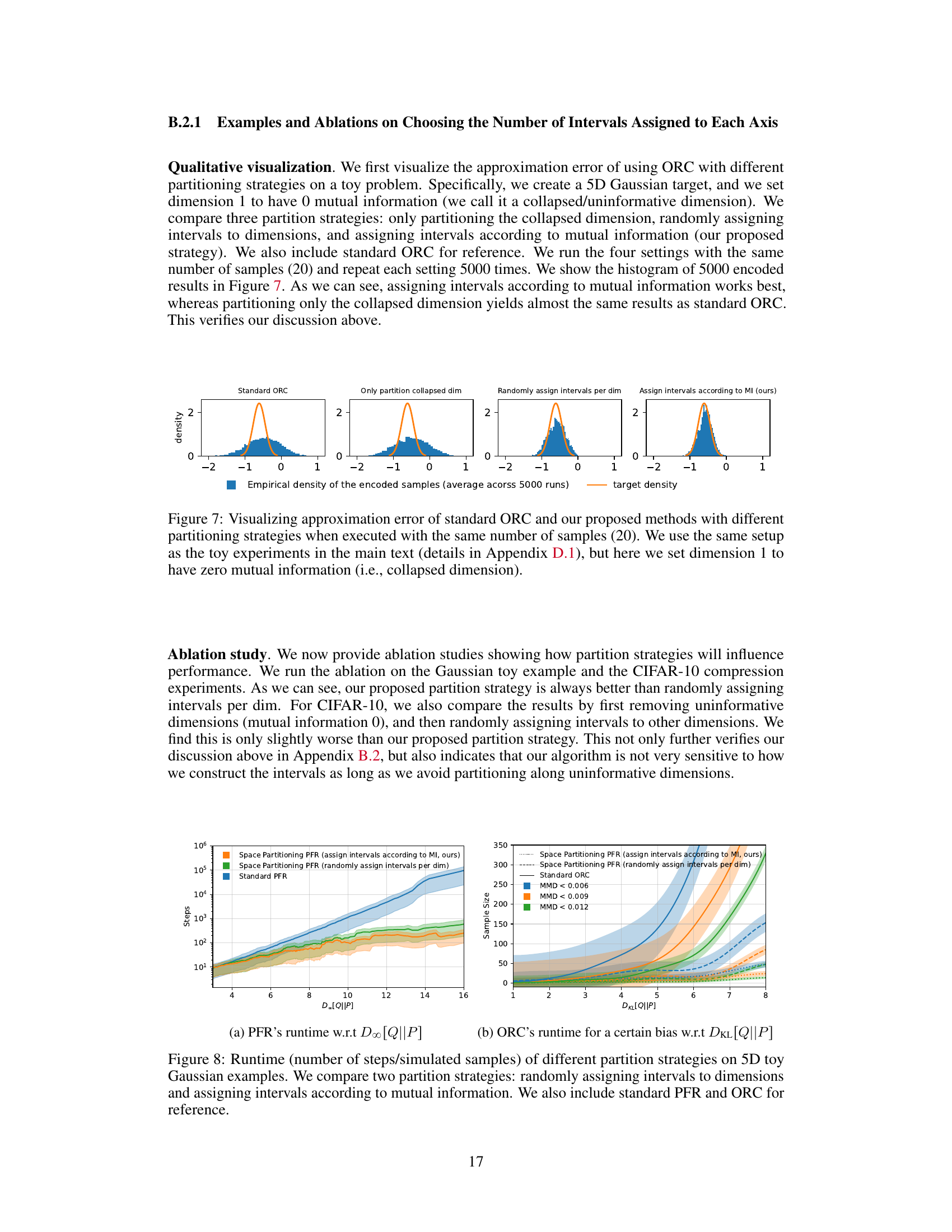
This figure compares the performance of standard ORC and three variations of the proposed space partitioning method for encoding samples from a 5D Gaussian distribution. The key difference between methods is how space is partitioned: only partitioning the ‘collapsed’ dimension (dimension with zero mutual information), random assignment of partitions, and assigning partitions according to mutual information. The figure shows histograms of the empirical densities of the encoded samples across 5000 runs for each method, with the target density overlaid in orange for comparison. The results show that assigning intervals according to mutual information outperforms other approaches.

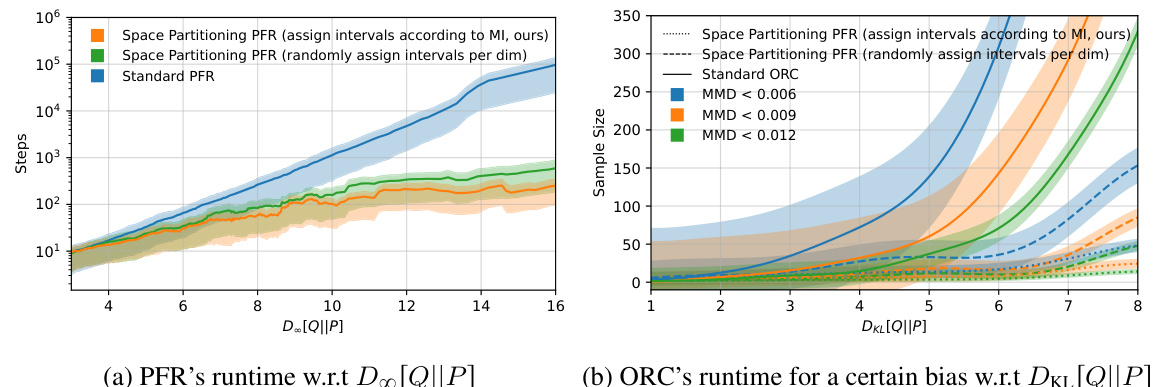
This figure compares the runtime and codelength of the standard Poisson Functional Representation (PFR) algorithm with the proposed space partitioning PFR algorithm. The experiment uses 5D synthetic Gaussian examples. The plots show that the space partitioning method significantly reduces the runtime while maintaining similar codelength compared to the standard PFR, especially as the KL divergence between the target and coding distributions increases.

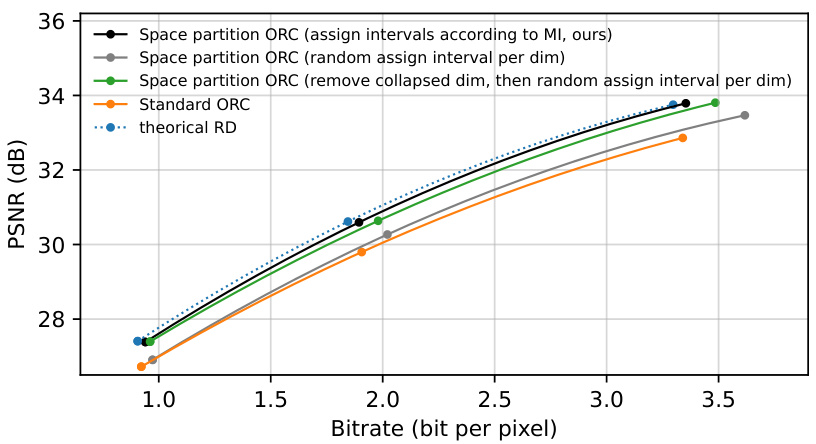
This figure compares the rate-distortion performance of the proposed space-partitioning algorithm with different partitioning strategies on the CIFAR-10 dataset using the RECOMBINER codec. It shows that the proposed method which assigns intervals according to mutual information performs best. The results highlight the algorithm’s robustness to the choice of partitioning strategy as long as uninformative dimensions are handled appropriately.

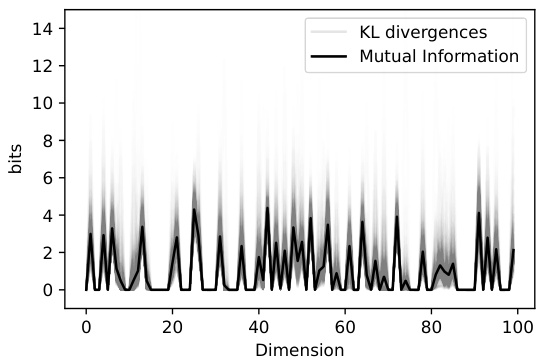
This figure shows the relationship between the dimension-wise mutual information and KL divergence for each test image. The KL divergence values are concentrated around the mutual information values. A zero mutual information value in a dimension results in a zero KL divergence in that dimension. This concentration is key for the space partitioning strategy’s runtime reduction because a close alignment between the mutual information and KL divergence leads to more efficient searching within the relevant regions of the space.

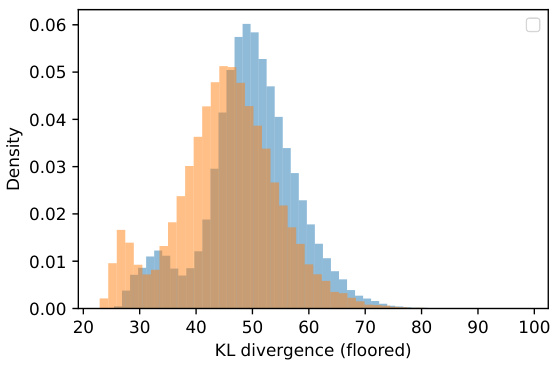
This histogram shows the distribution of the KL divergence for each block in a 2-block setup estimated from 60,000 MNIST training images. The slight difference between the two distributions is solely due to the random splitting of the latent space into blocks, highlighting the randomness in this process.

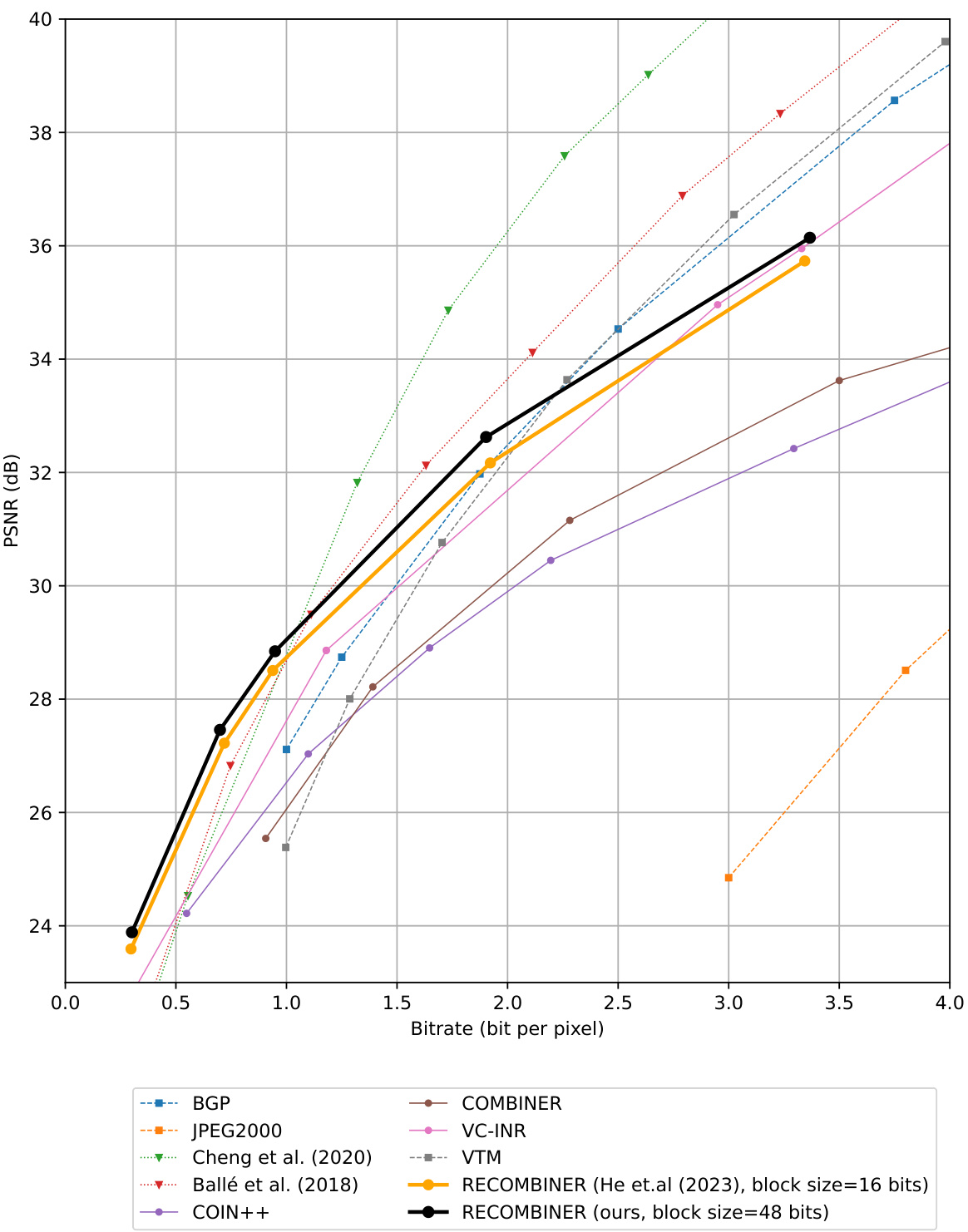
This figure compares the rate-distortion performance of the proposed algorithm with RECOMBINER and other codecs (classical, VAE-based, and INR-based) on CIFAR-10. The x-axis represents the bitrate, and the y-axis represents the PSNR. Solid lines indicate INR-based codecs, dotted lines represent VAE-based codecs, and dashed lines show classical codecs. The result demonstrates that the proposed method improves the performance of RECOMBINER.

Full paper

#