↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Large diffusion models are computationally expensive, hindering their use in resource-limited settings. Quantization, particularly 1-bit binarization, is a promising compression method, but applying it to diffusion models is challenging due to the models’ complex architecture and the inherent difficulty of representing rich generative features using only binary values. Existing methods struggle with full binarization, often leading to significant performance degradation.
BiDM tackles this challenge head-on with two key innovations: Timestep-friendly Binary Structure (TBS) and Space Patched Distillation (SPD). TBS leverages the temporal correlation of features across timesteps to improve representation efficiency in the binarized model. SPD addresses the spatial aspect by using a full-precision model as a guide for training, focusing on local image features during the optimization. This two-pronged approach enables BiDM to achieve the first successful full 1-bit binarization, significantly outperforming the state-of-the-art with remarkable efficiency gains and maintaining image generation quality.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on diffusion models, particularly those focused on model compression and efficient inference. By achieving full 1-bit quantization, it opens new avenues for deploying these powerful models on resource-constrained devices. It also provides valuable insights into handling the unique challenges of applying extreme quantization to generative models, and offers novel techniques such as the Timestep-friendly Binary Structure and Space Patched Distillation that are likely to influence future research in this area.
Visual Insights#

This figure illustrates the BiDM model’s architecture, highlighting its two key components: the Timestep-friendly Binary Structure (TBS) and the Space Patched Distillation (SPD). TBS, shown on the top half, addresses the temporal aspect of diffusion models by using learnable activation binarizers and cross-timestep connections to handle the highly timestep-correlated activation features. SPD, depicted in the bottom half, focuses on the spatial aspect by using patch-wise distillation to overcome challenges in matching binary features during the training process. The diagram visually represents how TBS improves the DM architecture temporally, and SPD enhances optimization spatially.
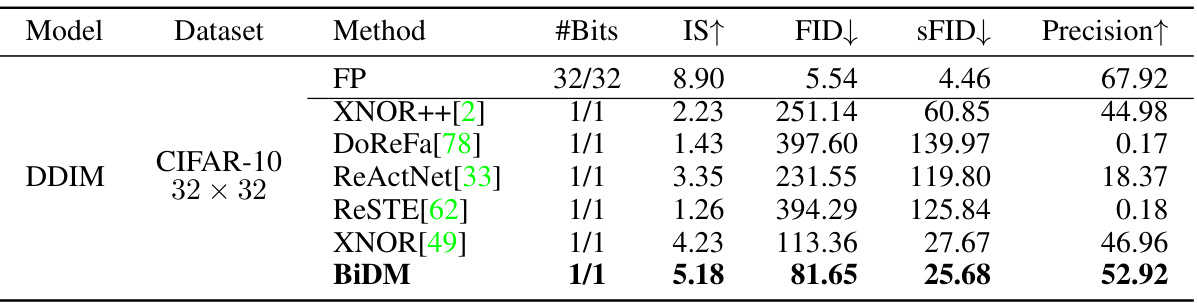
This table presents a comparison of different binarization methods applied to the DDIM model on the CIFAR-10 dataset. It shows the impact of various methods on image generation quality, measured using Inception Score (IS), Fréchet Inception Distance (FID), and Sliding Fréchet Inception Distance (sFID). The results are compared to a full-precision (32-bit) model, offering insight into the effectiveness of different 1-bit quantization techniques in preserving generative capabilities.
In-depth insights#
BiDM: 1-bit DM Limit#
The heading “BiDM: 1-bit DM Limit” suggests a research paper focusing on pushing the boundaries of quantization in diffusion models. BiDM likely represents a novel method achieving full binarization, meaning both weights and activations are quantized to only 1 bit. This is a significant achievement as 1-bit quantization (binarization) is the most extreme form of compression, typically resulting in substantial performance degradation in generative models like diffusion models (DMs). The paper likely details BiDM’s techniques to mitigate this issue, possibly involving architectural modifications or novel training strategies to maintain or even improve generation quality despite the severe data representation limitations. The “1-bit DM Limit” suggests the research either reaches the practical limit of binarization for DMs or proposes a method that significantly outperforms existing approaches, setting a new state-of-the-art for binarized DMs. The paper would likely benchmark BiDM against existing quantization methods for diffusion models, showcasing its superiority in terms of storage efficiency, inference speed, and surprisingly perhaps, even generative performance. The implications are significant, potentially enabling the deployment of DMs on resource-constrained devices such as mobile phones or embedded systems.
Timestep-Friendly TBS#
The concept of “Timestep-Friendly Binary Structure” (TBS) in the context of binarizing diffusion models addresses the challenge of maintaining high-quality image generation despite the significant information loss inherent in 1-bit quantization. The key insight is the temporal correlation of activation features within diffusion models, where features across consecutive timesteps exhibit high similarity. TBS leverages this correlation. Instead of using static binary quantizers, it incorporates learnable activation binarizers that dynamically adapt to the changing activation ranges across timesteps. This dynamic adaptation helps preserve richer information during binarization. Furthermore, TBS introduces cross-timestep feature connections, allowing information from preceding timesteps to enhance the representation capacity of the current timestep’s binarized features. This helps compensate for information loss due to extreme quantization, ultimately enabling higher-quality image generation with fully binarized diffusion models. The use of learnable components within TBS makes it adaptable and allows the model to implicitly learn optimal quantization strategies during training, thereby maximizing performance given the severe constraints of 1-bit representation.
Space Patched Distillation#
The proposed Space Patched Distillation (SPD) method cleverly addresses the challenges of conventional distillation when applied to fully binarized diffusion models. Conventional distillation struggles because the highly discrete nature of binarized features makes precise alignment with full-precision counterparts difficult. SPD ingeniously tackles this by dividing the feature maps into patches and applying attention-guided loss calculations patch-wise. This localized approach allows the model to prioritize the most crucial details, rather than focusing on minor discrepancies across the entire feature map. This spatial focus is particularly important for generative models like diffusion models, which exhibit spatial locality in their image generation process. SPD effectively guides the optimization of binarized features by using the full-precision model as a supervisor, providing a more nuanced guidance that the general L2 loss methods cannot provide. This spatial patching strategy enhances the learning process, leading to improved accuracy and efficiency in the binarized diffusion model.
BiDM Efficiency Analysis#
The BiDM Efficiency Analysis section would be crucial for demonstrating the practical impact of the proposed binarization method. It should present a detailed breakdown of both inference and training efficiency gains. For inference, quantifiable metrics such as FLOPS (floating-point operations per second), memory usage, and latency should be compared against baseline full-precision and other binarization methods. The analysis should highlight the speedup achieved and address any trade-offs between accuracy and efficiency. In the training efficiency aspect, the comparison should include training time, memory consumption during training, and potentially energy efficiency. Any overhead associated with the proposed Timestep-friendly Binary Structure (TBS) and Space Patched Distillation (SPD) should be carefully analyzed and justified in terms of their impact on overall training efficiency. Crucially, the section must present results showing that the speed/memory gains do not come at the cost of significant performance degradation; otherwise, the practical value of BiDM would be questionable.
BiDM Limitations#
BiDM, while achieving impressive results in fully binarizing diffusion models, exhibits limitations. Training efficiency is impacted by the introduction of Timestep-friendly Binary Structure and Space Patched Distillation, increasing computational demands compared to standard binarization methods. The reliance on distillation for optimization poses challenges, especially as matching binary and full-precision features remains difficult. Despite advancements, the method’s generalizability across diverse datasets and model architectures needs further validation. The accuracy improvements are significant but not perfect and may vary depending on specific datasets. Finally, the deployment efficiency relies on specialized libraries and hardware optimization, potentially limiting its immediate practical use in all settings. Further research is needed to address these limitations and improve training efficiency while broadening its applicability.
More visual insights#
More on figures

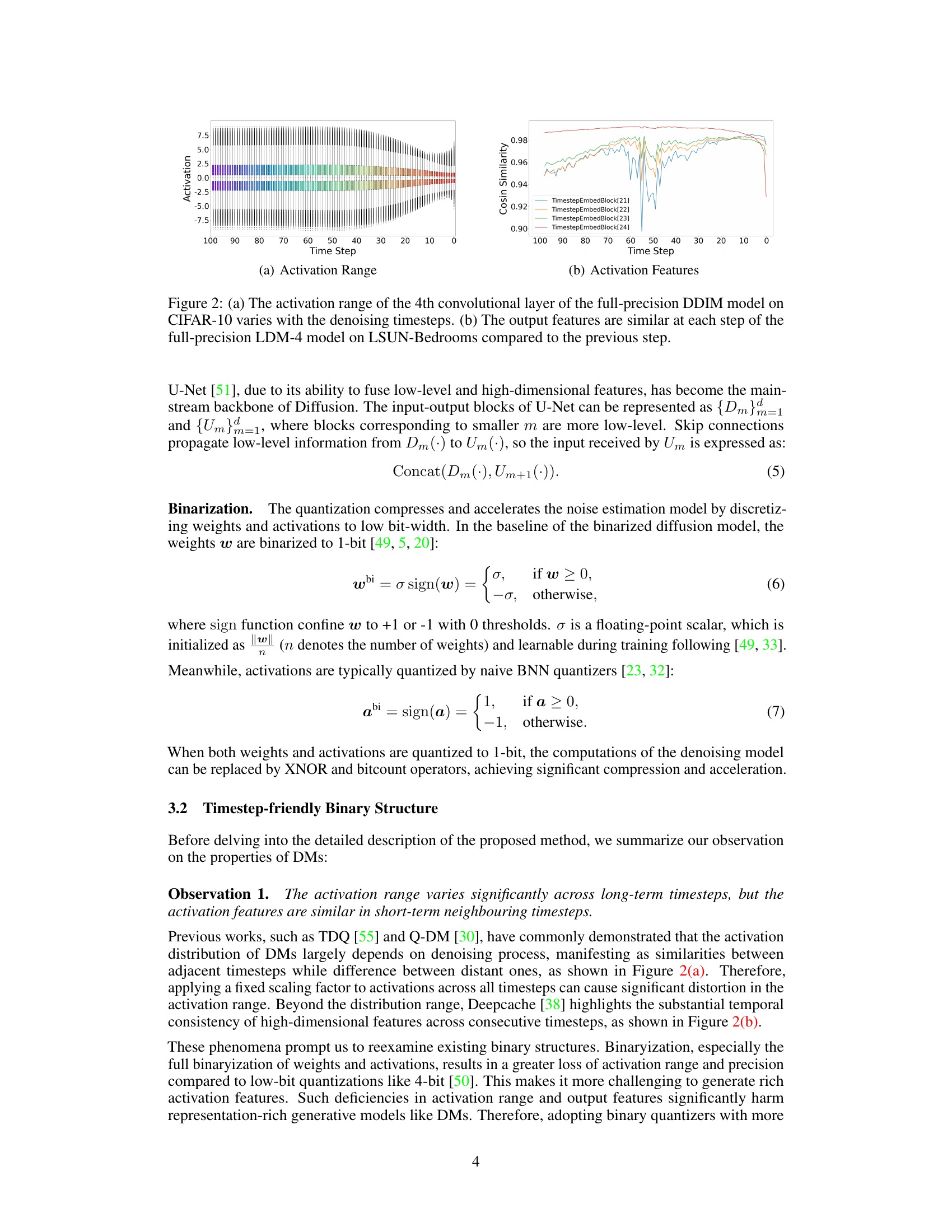
This figure shows two subfigures. (a) demonstrates the activation range variation in a convolutional layer of a DDIM model across different denoising timesteps, revealing a dynamic range. (b) illustrates that output features across consecutive timesteps in an LDM model maintain high similarity, indicating temporal consistency.

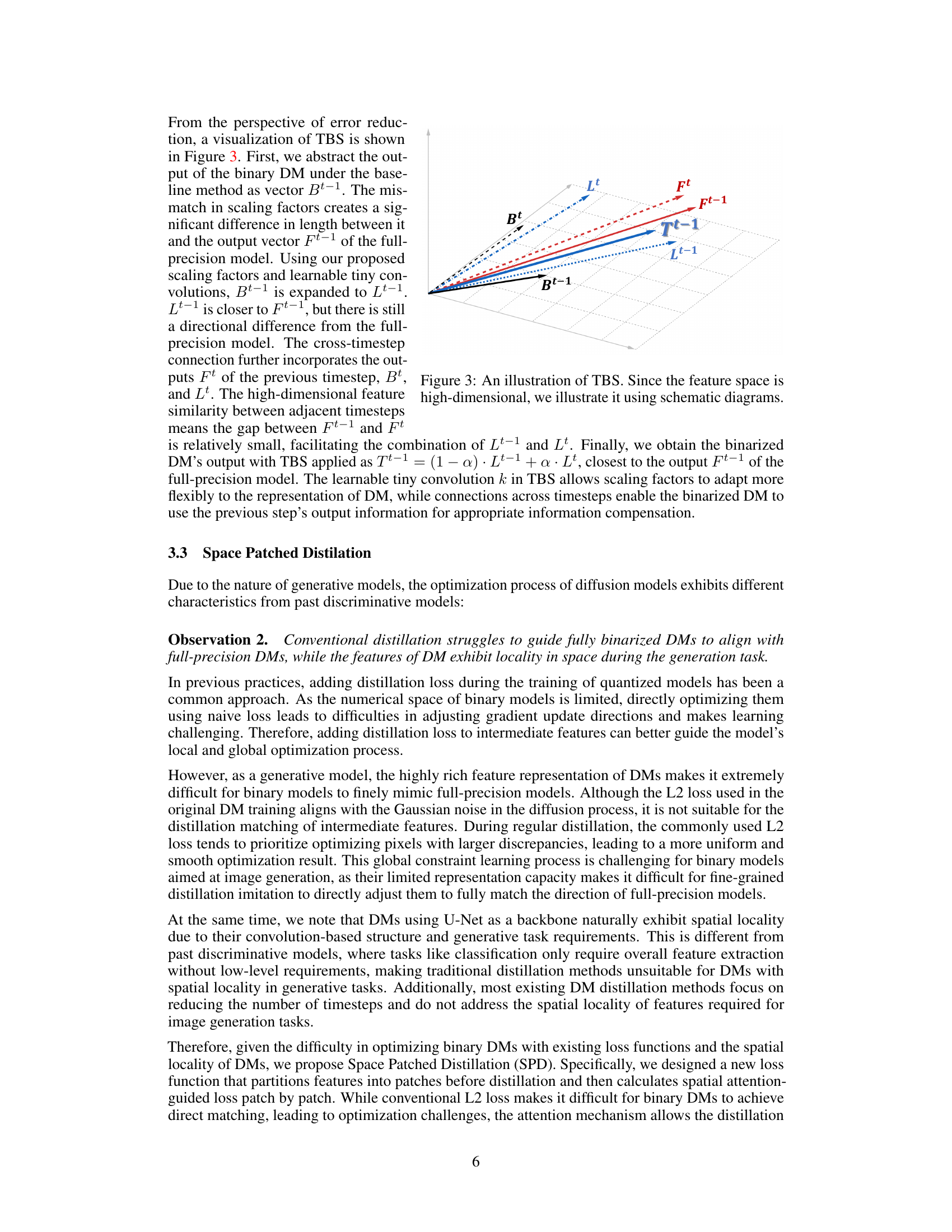
This figure illustrates the Timestep-friendly Binary Structure (TBS) method used in BiDM. It shows how TBS reduces error by using learnable scaling factors and cross-timestep connections. The black dashed line represents the output of the binary DM under the baseline method (Bt-1). The red dashed line represents the output of the full-precision model (Ft-1). The blue dotted line represents the expanded output after applying TBS scaling factors (Lt-1). The blue solid arrow shows the combination of Lt-1 and Lt (from the previous timestep), resulting in Tt-1, which is closer to the full-precision model’s output (Ft-1) than Bt-1.

This figure visualizes the output of the last TimeStepBlock in a Latent Diffusion Model (LDM) trained on the LSUN-Bedrooms dataset. It compares the output of a full-precision model (FP32), the difference between the full-precision and a binarized model (Diff), and the output after applying the proposed Space Patched Distillation (SPD) method (SPD). The visualization shows that SPD helps to reduce the difference between the full-precision and binarized model outputs, suggesting its effectiveness in improving the accuracy of binarized diffusion models.

This figure shows sample images generated by different methods, including several baselines (XNOR++, ReActNet, ReSTE, XNOR) and BiDM, the proposed method. The W1A1 setting signifies that both weights and activations are binarized to 1-bit. The figure visually demonstrates BiDM’s significant improvement over the baselines, producing clear and recognizable images, unlike the noisy or meaningless outputs from the other methods. This highlights the effectiveness of BiDM in achieving high-quality image generation despite the extreme compression of binarization.

This figure shows the training loss curves for eight different training settings (denoted by numbers 1 through 8), corresponding to the settings described in Table 9 of the paper. The left subplot (a) plots the training loss against the number of training iterations, while the right subplot (b) plots the training loss against the training time (in seconds). The different lines represent different settings, allowing for a comparison of training convergence speed and efficiency across various configurations.

This figure compares the image generation results of BiDM with several baseline methods (XNOR++, ReActNet, ReSTE, and XNOR) on the LSUN-Bedrooms dataset. Each row represents a different method, and the images in each row are samples generated by that method. The figure visually demonstrates the superior image generation quality achieved by BiDM compared to the baselines. The baseline methods show various artifacts, such as blurry images or incomplete object generation, while BiDM generates more realistic and coherent bedroom images.

This figure displays the image generation results from several different models on the LSUN-Churches dataset. The models compared include XNOR++, ReActNet, ReSTE, XNOR, and the authors’ proposed BiDM model. Each row shows the output of a different model. The goal is to visually compare the image quality generated by different binarization techniques against the authors’ proposed method (BiDM). The difference in the quality of generated images highlights the effectiveness of the BiDM approach.

This figure shows the image generation results of different methods on the FFHQ dataset. The top row shows the results of XNOR++, followed by ReActNet, ReSTE, XNOR, and BiDM. The image quality improves significantly as we move down the rows to BiDM, indicating the superior performance of BiDM in generating high-quality images even with full binarization.
More on tables

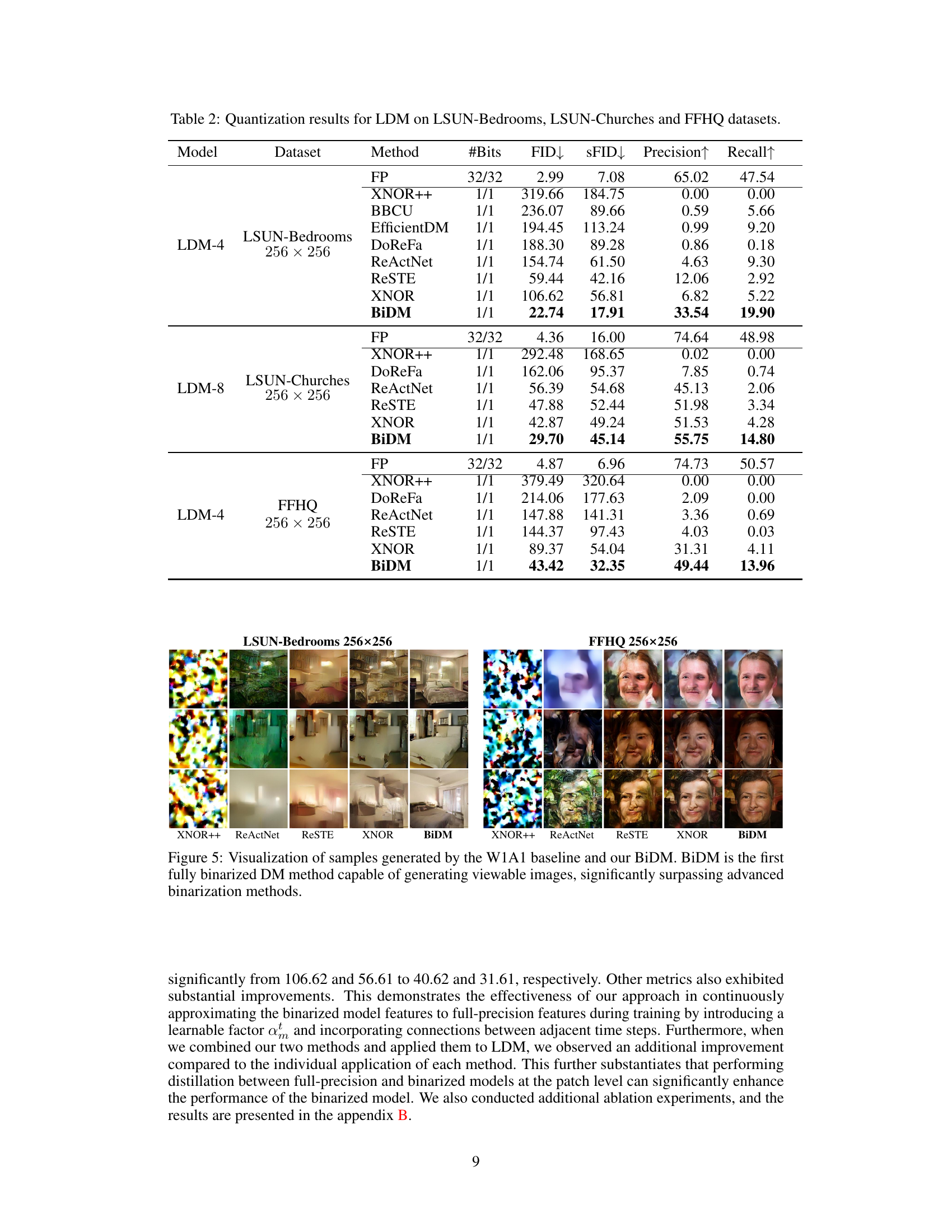
This table presents the results of quantization experiments on three different datasets using the Latent Diffusion Model (LDM). It compares the performance of the proposed BiDM method against various baseline methods across different metrics, including FID, sFID, Precision, and Recall. The datasets used are LSUN-Bedrooms, LSUN-Churches, and FFHQ, all at a resolution of 256 x 256. The #Bits column shows the number of bits used for quantization, demonstrating the extreme compression capabilities of BiDM, which is fully binarized (1 bit). The results illustrate the significant improvement achieved by BiDM in generating high-quality images compared to other methods, highlighting its advantages in terms of both accuracy and efficiency.

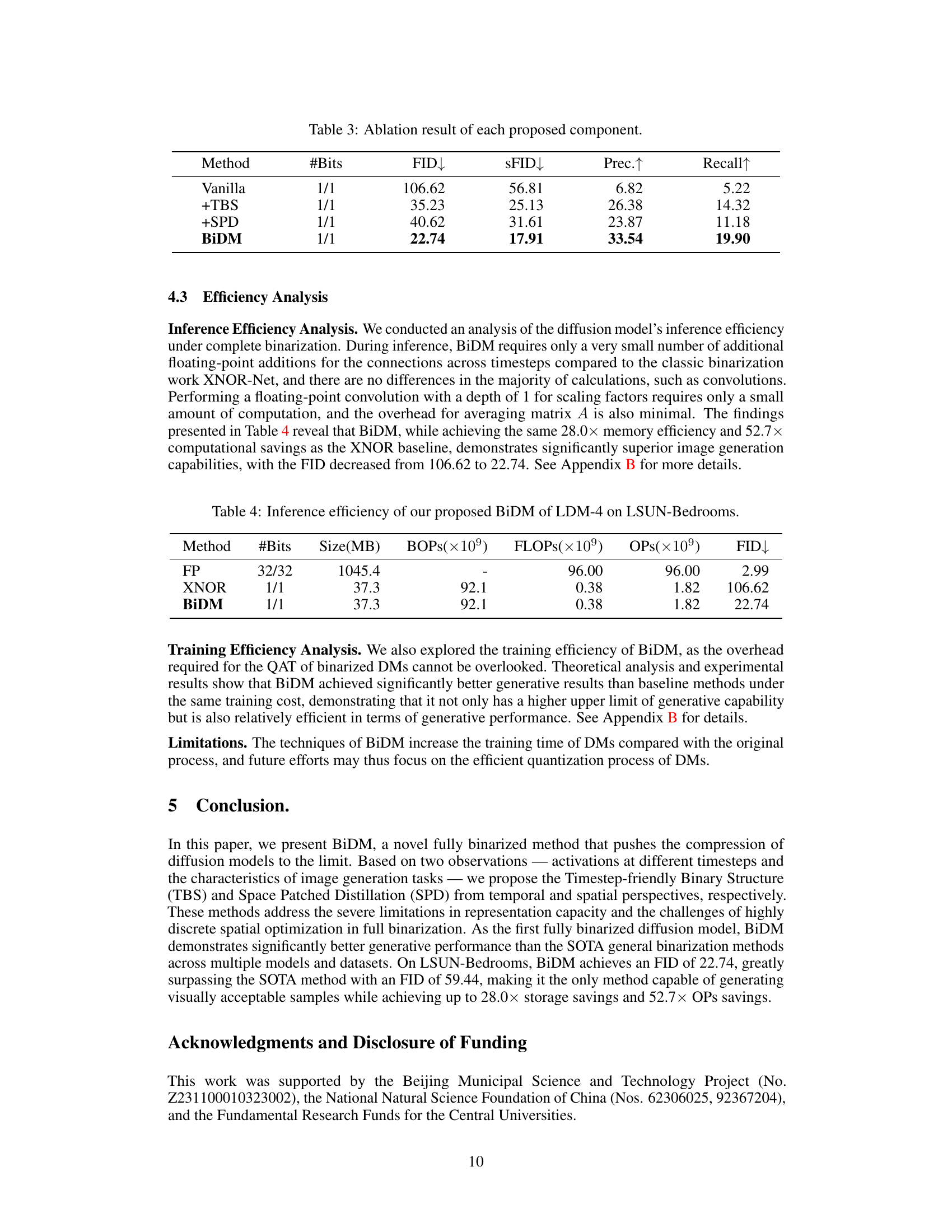
This table presents the ablation study results of the proposed BiDM method on the LSUN-Bedrooms dataset. It shows the impact of each component (TBS and SPD) on the FID, sFID, Precision, and Recall metrics. The ‘Vanilla’ row shows the results with only the baseline binarization, while subsequent rows show incremental improvements with the addition of TBS and SPD. The final row, BiDM, represents the combination of both techniques showing the cumulative performance gains.

This table presents the inference efficiency comparison between the full-precision model (FP), the XNOR baseline, and the proposed BiDM model. It shows the number of bits, model size, binary operations per second (BOPs), floating point operations (FLOPs), total operations (OPs), and Fréchet Inception Distance (FID). The table highlights that BiDM achieves significant improvements in FID while maintaining comparable memory and computational efficiency to the XNOR baseline.

This table presents the ablation study results focusing on the impact of making the scaling factor ‘k’ learnable within the XNOR baseline network. It compares the performance metrics (FID, sFID, Precision, Recall) of the original XNOR baseline (Vanilla) against the modified version where ‘k’ is learnable. The results highlight a significant improvement in FID and sFID when ‘k’ is learnable, indicating the effectiveness of this modification.

This table presents the ablation study results on the impact of varying the number of TBS (Timestep-friendly Binary Structure) connections in the BiDM model. It shows that adding cross-timestep connections consistently improves the model’s performance across different metrics (FID, sFID, Precision, Recall), with optimal results being achieved with either 1 or 8 connections.

This table presents the Ablation Study results of different distillation strategies used in BiDM. Specifically, it compares the performance of using the L2 loss function versus the proposed Space Patched Distillation (SPD) loss function. The results are evaluated using FID, sFID, Precision, and Recall metrics. The table shows that SPD outperforms the L2 loss, demonstrating the effectiveness of the proposed SPD method in improving the model’s ability to align with the full-precision model during optimization.

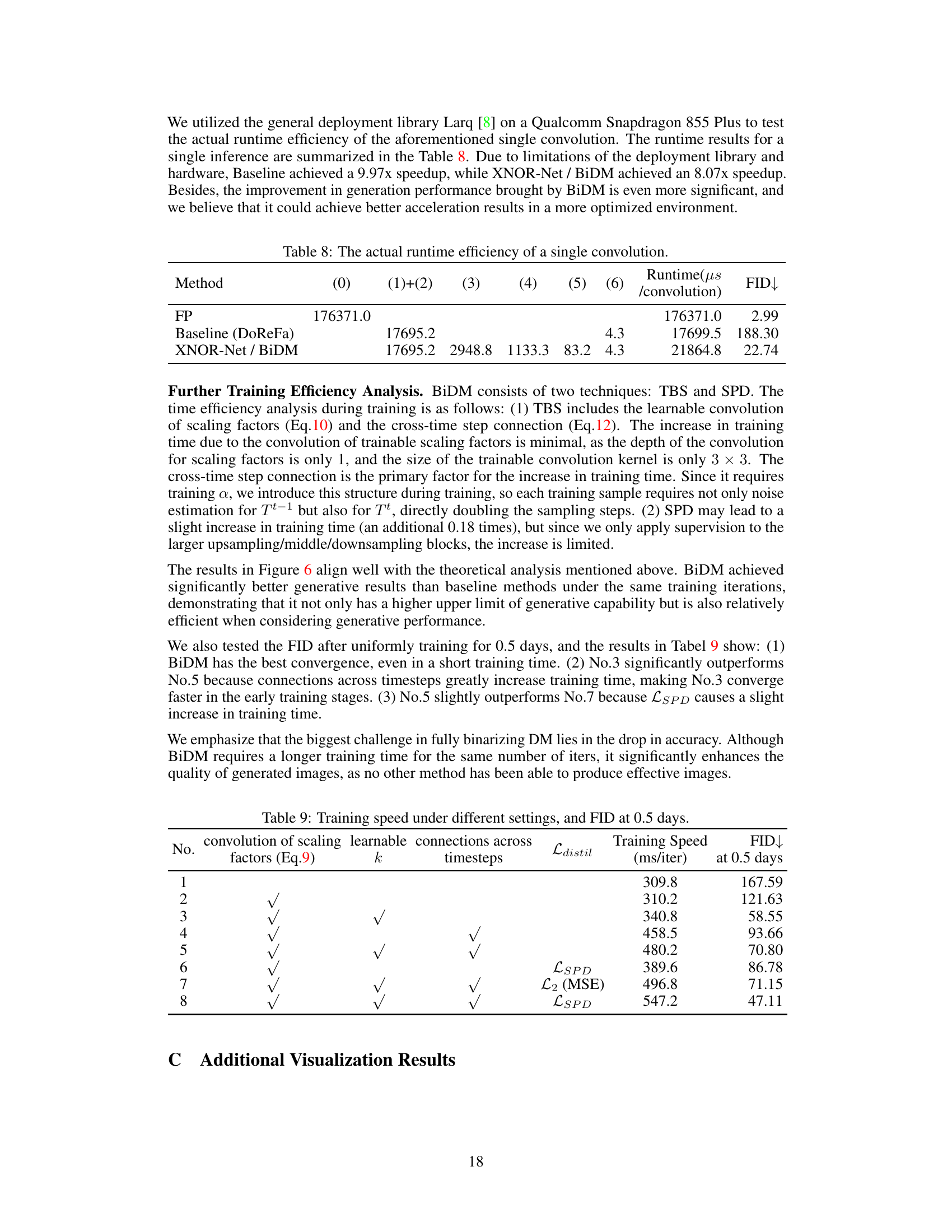
This table shows the actual runtime efficiency (in microseconds) of a single convolution operation for different methods: FP (full precision), Baseline (DoReFa), and XNOR-Net/BiDM (the proposed method). It also lists the FID (Fréchet Inception Distance) for each method, demonstrating the tradeoff between speed and accuracy. BiDM shows a significant reduction in FID compared to the baseline, indicating improved image generation quality, while also showing improved speed compared to the full-precision method. The runtime is measured on a Qualcomm Snapdragon 855 Plus.
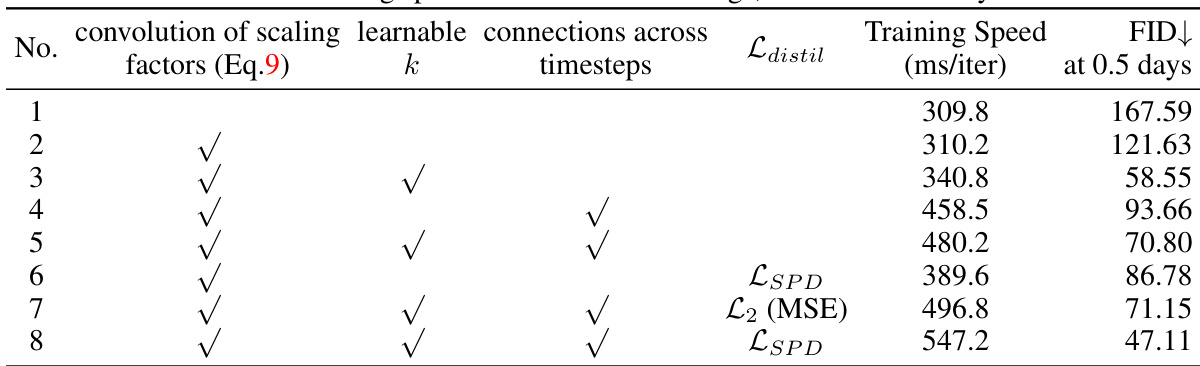
This table presents the results of quantization experiments performed on three different datasets using the Latent Diffusion Model (LDM). It compares the performance of different quantization methods (including the proposed BiDM) across various metrics such as Fréchet Inception Distance (FID), Sliding Fréchet Inception Distance (sFID), Precision, and Recall, for different bit-widths (#Bits). The results highlight the improvements achieved by BiDM over the existing state-of-the-art binarization methods.
Full paper#