TL;DR#
Transformers are powerful deep learning models, but their learning processes are not fully understood. A key challenge is that their training often converges to suboptimal solutions, i.e., local minima, rather than the optimal global minimum. The paper tackles this problem by examining the relationship between data properties (assuming Markovian input sequences) and model initialization. Early works have investigated these connections using this perspective to study in-context learning. However, a comprehensive analysis highlighting the role of initialization is missing.
This paper focuses on single-layer transformers with first-order Markov chain inputs. Using gradient flow analysis, it proves that the model’s convergence depends critically on the data’s ‘switching factor’ and initialization. Importantly, it establishes precise conditions for convergence to either global or local minima, and offers practical guidelines for parameter initialization to enhance the likelihood of achieving a globally optimal solution. The findings are backed by empirical evidence and clearly highlight the crucial role of initialization.
Key Takeaways#
Why does it matter?#
This paper is crucial because it provides a novel understanding of how transformer models learn, specifically focusing on the role of initialization and data properties. This has significant implications for improving training efficiency and model performance. The analysis sheds light on the complex interactions between initialization, data characteristics, and the resulting model behavior, which is critical for both theoretical and practical advancements in transformer-based models. It also identifies key open problems for future research.
Visual Insights#

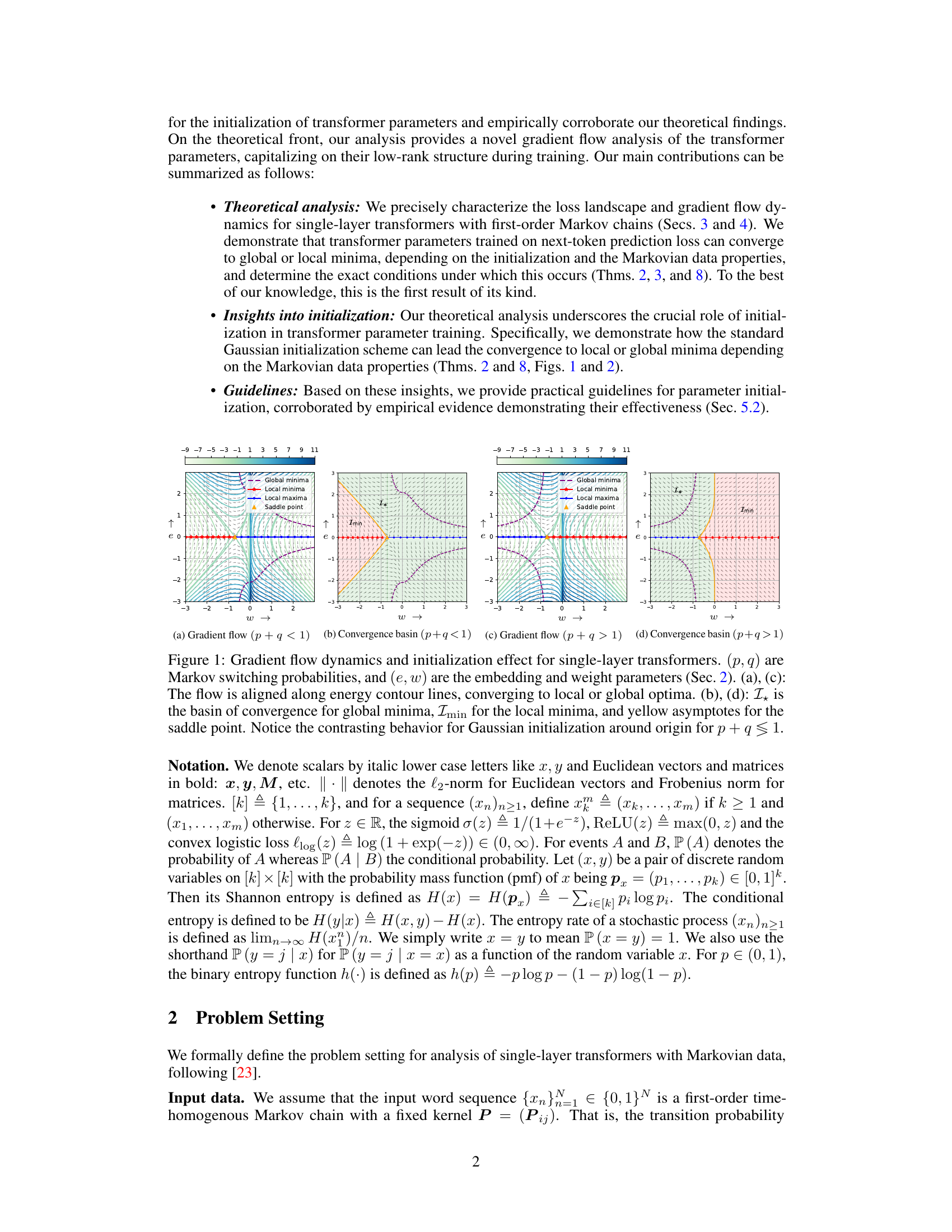
🔼 This figure visualizes the gradient flow dynamics and the effect of initialization on the convergence of single-layer transformers trained on next-token prediction loss. It shows how the convergence to either global or local minima depends on the Markov switching probabilities (p, q) and the initialization of the embedding and weight parameters (e, w). The gradient flow is shown to align with energy contour lines, leading to different optima depending on the initial conditions. The convergence basins for global and local minima, as well as saddle points, are also illustrated. The figure highlights that the behavior near the origin differs significantly depending on whether the sum of the Markov switching probabilities (p+q) is less than or equal to 1.
read the caption
Figure 1: Gradient flow dynamics and initialization effect for single-layer transformers. (p, q) are Markov switching probabilities, and (e, w) are the embedding and weight parameters (Sec. 2). (a), (c): The flow is aligned along energy contour lines, converging to local or global optima. (b), (d): Ix is the basin of convergence for global minima, Imin for the local minima, and yellow asymptotes for the saddle point. Notice the contrasting behavior for Gaussian initialization around origin for p + q ≤ 1.

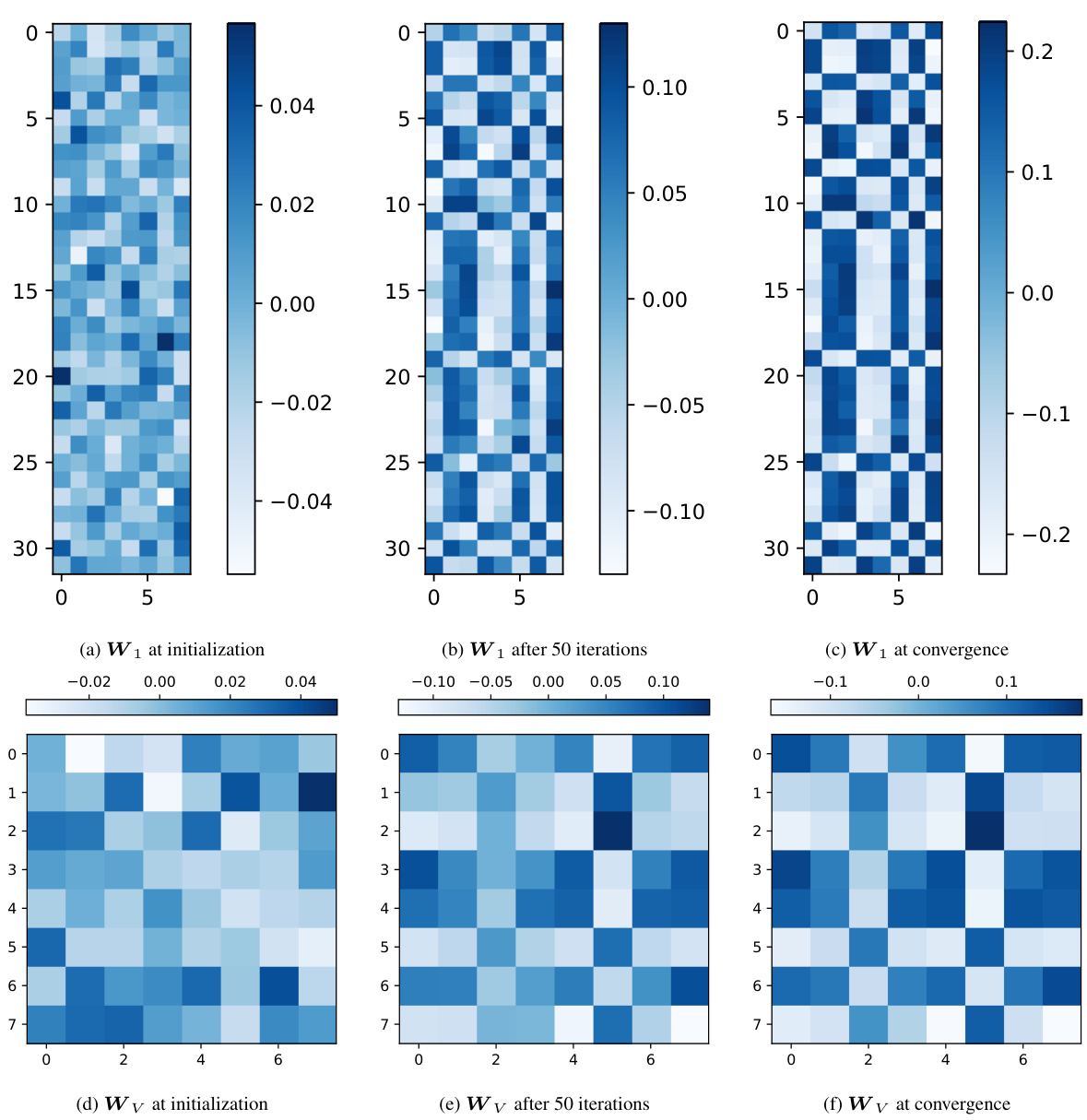
🔼 This table lists the parameters used in the single-layer transformer architecture described in the paper, along with their corresponding matrix shapes. The shapes are expressed in terms of the embedding dimension (d) and the sequence length (N). This table provides a concise summary of the parameter dimensions for those familiar with transformer architectures.
read the caption
Table 1: Parameters in the transformer architecture with their shape.
In-depth insights#
Transformer Dynamics#
Analyzing transformer dynamics involves understanding how these models learn and adapt to data. Understanding the loss landscape is crucial; it reveals the existence of local and global minima, influencing the model’s convergence. Initialization strategies significantly impact the training process, potentially leading to convergence to local minima, hindering optimal performance. Gradient flow analysis provides insights into the trajectory of parameter updates during training. Studying these dynamics helps in improving initialization techniques to promote convergence to global minima and enhance performance, and potentially to design more robust and efficient training algorithms that navigate the complex loss landscape effectively. Research in this area helps to reveal the implicit biases of transformers, furthering our understanding of why and how these models perform so well in various tasks.
Markov Chain Impact#
The impact of employing Markov chains in analyzing transformer models hinges on their ability to capture the sequential nature of data. By modeling input sequences as Markov chains, researchers gain a valuable tool for understanding how transformers process information and learn long-range dependencies. This approach allows for a more formal mathematical analysis of the learning dynamics, loss landscapes, and convergence properties of the models. This is particularly beneficial when dealing with complex sequential data, where traditional methods may fall short. Furthermore, this perspective simplifies the analysis of the attention mechanism. However, the choice of Markov chain order (first-order, higher-order) significantly impacts the accuracy and tractability of the model, posing a trade-off between model complexity and analytical feasibility. Limitations exist in the scope of Markov chain models, as they may not fully encompass all the nuances of transformer architecture and learning behavior. Despite these limitations, the Markov chain approach offers valuable insights into the workings of these powerful models and guides further research into their fundamental characteristics.
Initialization Effects#
The study’s focus on initialization effects in transformer models reveals crucial insights into the model’s learning dynamics. The choice of initialization significantly impacts whether the model converges to a global minimum or gets stuck in a suboptimal local minimum. This is particularly important for first-order Markov chains, where the data’s structure heavily influences the loss landscape. Gaussian initialization, while common, can hinder convergence to the global optimum, leading to subpar performance. This highlights a need for more sophisticated initialization strategies tailored to the data characteristics and the desired model behavior. The findings underscore the importance of not only the architecture and training process but also initialization’s subtle, yet profound effect. The authors demonstrate that careful selection of initialization parameters based on theoretical findings can guide the model toward optimal solutions and improve overall performance. This work sheds light on a previously underestimated aspect of training transformers, paving the way for advanced techniques in optimizing model performance.
Gradient Flow Analysis#
Gradient flow analysis offers a powerful lens to understand the learning dynamics of transformer models, particularly their convergence behavior. By viewing gradient descent as a continuous-time process, this approach reveals the trajectory of parameter updates over time. Analyzing the gradient flow unveils crucial information about the loss landscape, including the identification of critical points such as local minima, global minima, and saddle points. Furthermore, gradient flow analysis provides insights into the effects of parameter initialization, showcasing how different initializations can lead to vastly different convergence outcomes, potentially resulting in the model getting trapped in local minima. In the context of transformers, understanding the gradient flow on low-rank manifolds may offer considerable simplification in analyzing the learning dynamics, which are inherently high dimensional and complex. Ultimately, gradient flow analysis is a valuable tool for both theoretical analysis and practical guidance in training more effective transformer models, suggesting optimal initialization strategies and illuminating how model architecture interacts with the learning process itself.
Future Research#
The paper’s conclusion points towards exciting avenues for future research. A key area is extending the theoretical analysis to more complex scenarios. This includes investigating higher-order Markov chains, moving beyond the first-order model explored here, and examining multi-state Markov chains, going beyond binary input data. Another important direction is to analyze the learning dynamics in deeper transformer models. The current work focuses on single-layer transformers; scaling the theoretical framework to deeper networks presents a significant challenge but offers potential for deeper insights into their behavior. Finally, investigating the impact of different initialization strategies, beyond the standard Gaussian initialization and the proposed guidelines, could further illuminate the training dynamics and convergence properties of transformers, potentially yielding more effective and robust training methods. Empirically validating these extensions is crucial; while this paper provides compelling empirical results for a simplified setting, broader, more realistic experiments are needed to confirm the generalizability of these findings.
More visual insights#
More on figures

🔼 This figure visualizes the gradient flow dynamics for a single-layer transformer with canonical parameters (e, w, a) ∈ R³, where ‘a’ represents the attention scalar. Panels (a) and (c) show the gradient flow for p+q < 1 and p+q > 1, respectively, illustrating how the flow converges to either local or global minima depending on the initialization and the Markov data properties. Panels (b) and (d) display the corresponding energy manifold and minima locations, further highlighting the influence of initialization and data properties on the convergence behavior.
read the caption
Figure 2: Gradient flow dynamics for the canonical parameters θ = (e, w, a) ∈ R³ with the attention scalar a. Notice the contrasting behavior for Gaussian initialization around origin for p + q smaller and greater than one. For an enhanced view of the flow near the origin, please refer to Fig. 5.
🔼 This figure shows the gradient flow dynamics and the effect of initialization for single-layer transformers. It visualizes how the parameters (embedding ’e’ and weight ‘w’) converge to either global or local minima depending on the Markov switching probabilities (‘p’ and ‘q’). Panels (a) and (c) show the gradient flow aligned with energy contours, while panels (b) and (d) illustrate the basins of convergence for different optima. A key observation is the contrasting behavior of Gaussian initialization around the origin for cases where p+q is less than or equal to 1.
read the caption
Figure 1: Gradient flow dynamics and initialization effect for single-layer transformers. (p, q) are Markov switching probabilities, and (e, w) are the embedding and weight parameters (Sec. 2). (a), (c): The flow is aligned along energy contour lines, converging to local or global optima. (b), (d): Ix is the basin of convergence for global minima, Imin for the local minima, and yellow asymptotes for the saddle point. Notice the contrasting behavior for Gaussian initialization around origin for p + q ≤ 1.

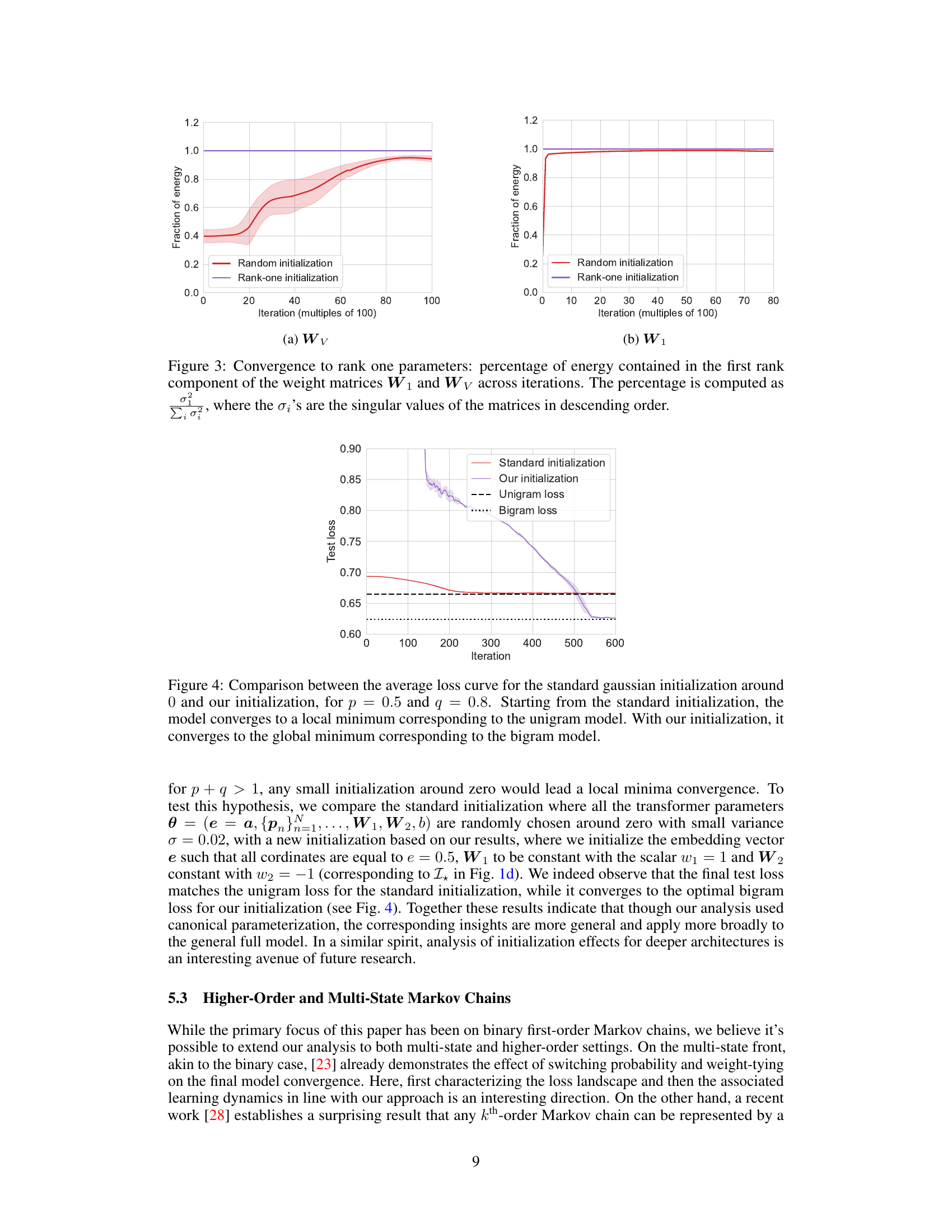
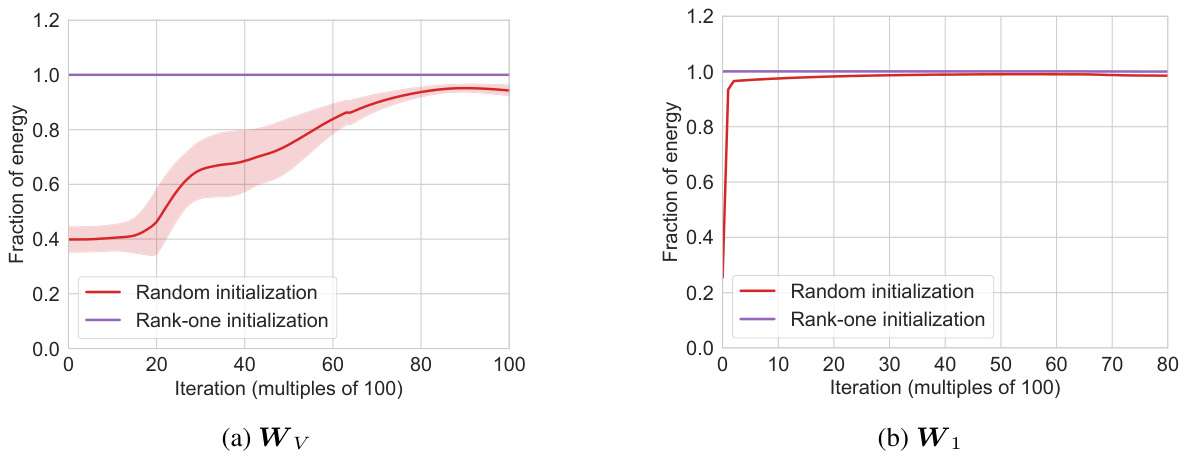
🔼 This figure compares the training loss curves for a single-layer transformer model trained on a first-order Markov chain with p=0.5 and q=0.8, using two different initialization methods: standard Gaussian initialization and the initialization strategy proposed in the paper. The results demonstrate that the standard initialization leads to convergence to a local minimum representing a unigram model, while the proposed initialization converges to the global minimum corresponding to the true bigram model.
read the caption
Figure 4: Comparison between the average loss curve for the standard gaussian initialization around 0 and our initialization, for p = 0.5 and q = 0.8. Starting from the standard initialization, the model converges to a local minimum corresponding to the unigram model. With our initialization, it converges to the global minimum corresponding to the bigram model.
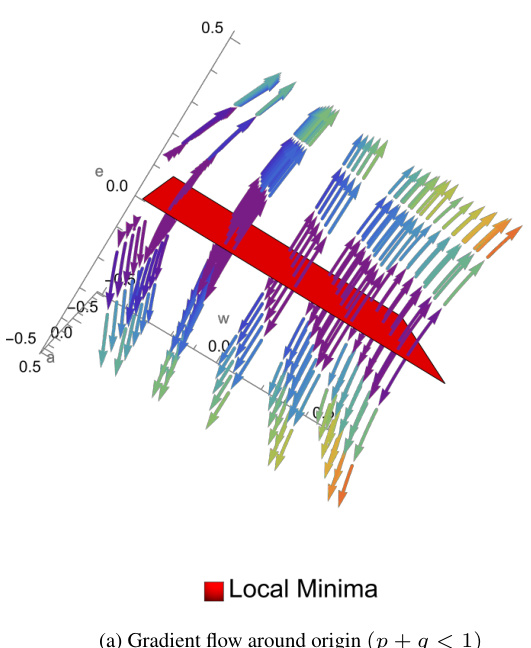
🔼 This figure shows the gradient flow dynamics for a single-layer transformer with canonical parameters (e, w, a) ∈ R³, where ‘a’ represents the attention scalar. The left two subfigures (a and b) illustrate the gradient flow for p+q < 1 and the right two subfigures (c and d) illustrate the flow for p+q >1. The contrasting behavior of Gaussian initialization around the origin for these two cases is highlighted. For a more detailed view of the flow near the origin, the reader is referred to Figure 5.
read the caption
Figure 2: Gradient flow dynamics for the canonical parameters θ = (e, w, a) ∈ R³ with the attention scalar a. Notice the contrasting behavior for Gaussian initialization around origin for p + q smaller and greater than one. For an enhanced view of the flow near the origin, please refer to Fig. 5.
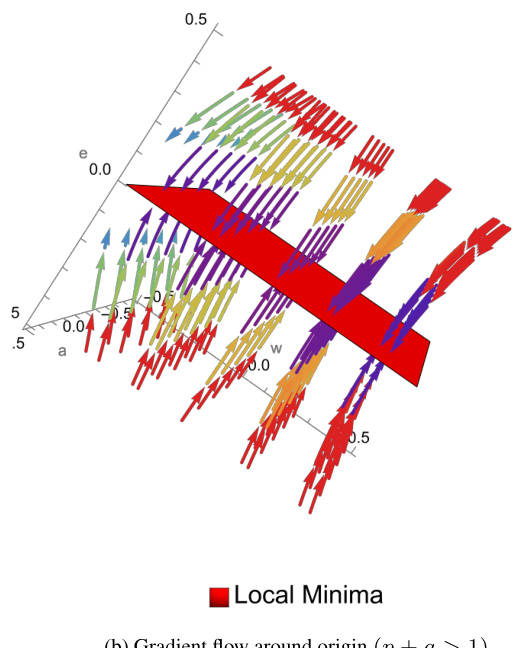
🔼 This figure shows gradient flow dynamics for single-layer transformers with first-order Markov chains. The parameters are (e, w, a), representing embedding, weight, and attention, respectively. The plots illustrate how the gradient flow behaves differently depending on the switching factor (p+q) and initial parameter values. Notably, the behavior differs significantly for Gaussian initialization near the origin; it contrasts between p+q > 1 and p+q < 1. Figure 5 provides a closer look at the dynamics near the origin.
read the caption
Figure 2: Gradient flow dynamics for the canonical parameters θ = (e, w, a) ∈ R³ with the attention scalar a. Notice the contrasting behavior for Gaussian initialization around origin for p + q smaller and greater than one. For an enhanced view of the flow near the origin, please refer to Fig. 5.
🔼 This figure shows the gradient flow dynamics and the effect of initialization on the convergence of single-layer transformers trained on next-token prediction loss. The plots visualize the gradient flow (a, c) and convergence basins (b, d) in the parameter space (embedding parameter ’e’ and weight parameter ‘w’) for different Markov switching probabilities (‘p’ and ‘q’). The behavior of the system changes depending on whether the sum of switching probabilities (p+q) is less than or greater than 1. For p+q ≤ 1, Gaussian initialization around the origin leads to convergence to global minima; for p+q > 1, Gaussian initialization can lead to local minima.
read the caption
Figure 1: Gradient flow dynamics and initialization effect for single-layer transformers. (p, q) are Markov switching probabilities, and (e, w) are the embedding and weight parameters (Sec. 2). (a), (c): The flow is aligned along energy contour lines, converging to local or global optima. (b), (d): Ix is the basin of convergence for global minima, Imin for the local minima, and yellow asymptotes for the saddle point. Notice the contrasting behavior for Gaussian initialization around origin for p + q ≤ 1.

🔼 This figure shows the gradient flow dynamics and the effect of initialization on single-layer transformers’ convergence to either local or global minima. The plots visualize how the gradient flow (aligned along energy contour lines) converges depending on the Markov switching probabilities (p,q) and the transformer parameters (embedding (e) and weight (w)). Panels (a) and (c) illustrate gradient flow for different (p,q) values. Panels (b) and (d) show the convergence basins (regions of initialization leading to specific optima) for the same (p,q) values, highlighting the role of initialization in reaching either global or local minima.
read the caption
Figure 1: Gradient flow dynamics and initialization effect for single-layer transformers. (p, q) are Markov switching probabilities, and (e, w) are the embedding and weight parameters (Sec. 2). (a), (c): The flow is aligned along energy contour lines, converging to local or global optima. (b), (d): Ix is the basin of convergence for global minima, Imin for the local minima, and yellow asymptotes for the saddle point. Notice the contrasting behavior for Gaussian initialization around origin for p + q ≤ 1.
Full paper#