↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Diffusion models are leading image generation methods, but training them efficiently remains a challenge. Prior work showed bounds polynomial in dimension and error, making large-scale training computationally expensive. This study addresses this limitation focusing on the sample complexity (how many data points are needed) of training score-based diffusion models using neural networks. The core problem lies in accurately estimating score functions at various time steps during the diffusion process. Inaccurate estimation leads to poor sample quality.
The researchers tackle this by introducing a new, more robust measure for score estimation. Instead of focusing on the traditional L2 error metric, they use an outlier-robust metric. This new approach significantly improves sample complexity bounds. They show exponential improvements in the dependence on Wasserstein error and depth of the network, and show a polylogarithmic dependence on the dimension, providing a major advancement in training efficiency. This has significant implications for building high-quality generative models more efficiently.
Key Takeaways#
Why does it matter?#
This paper is crucial because it significantly improves our understanding of training diffusion models, a dominant approach in image generation. The exponential improvement in sample complexity bounds, particularly concerning Wasserstein error and depth, directly impacts the efficiency and scalability of training these models. This opens avenues for creating more efficient and higher-quality generative models, which is highly relevant to the current AI research landscape.
Visual Insights#
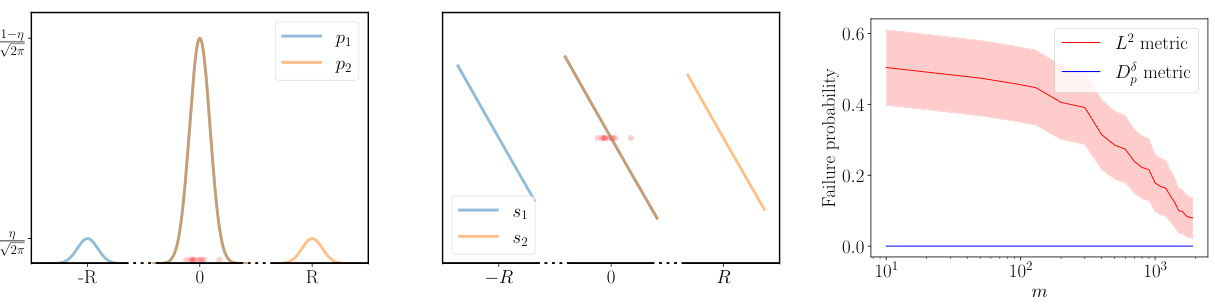
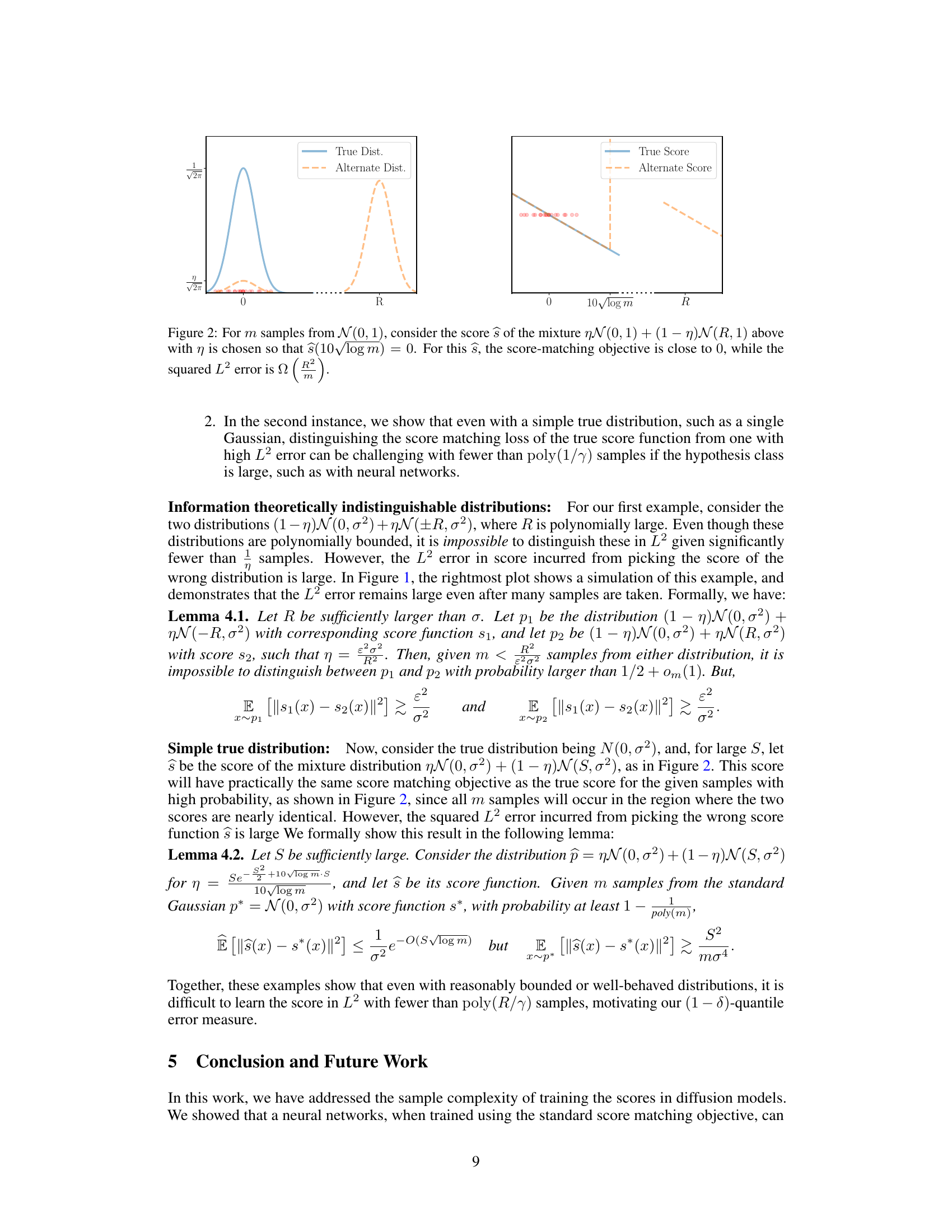
This figure shows an example where it is difficult to learn the score in L2, even though learning to sufficient accuracy for sampling is possible. The left panel shows two distributions p1 and p2, which are very similar to each other. Despite this, the score functions s1 and s2 are quite different. The right panel illustrates how the probability that the empirical risk minimizer (ERM) has error larger than 0 scales with the number of samples (m). This probability is significantly higher for the L2 metric compared to the proposed Do metric.
Full paper#