What do Graph Neural Networks learn? Insights from Tropical Geometry

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it bridges the gap in our understanding of Graph Neural Networks (GNNs), addressing fundamental questions about their capabilities that have remained elusive. It provides theoretical insights into GNN expressivity and efficiency, potentially leading to the design of more efficient and powerful GNN architectures. The findings are relevant to a broad range of researchers working with GNNs across diverse applications and promote deeper understanding of their underlying mathematical foundations.

Visual Insights

#

This figure summarizes the key theoretical contributions of the paper. It highlights the use of tropical geometry to analyze ReLU message-passing neural networks (MPNNs). The figure shows that the work characterizes the class of functions learned by ReLU MPNNs, establishes bounds on their geometric complexity, introduces new architectures, and characterizes their decision boundaries. These contributions address limitations of existing methods, such as the Weisfeiler-Lehman (WL) test, for understanding the capabilities of GNNs.

This table compares the complexity of four different ReLU MPNN architectures (Local, Global, Constant, and Hybrid) and a previous method from existing works for representing tropical signomial functions (TSFs). It details the number of message passing layers, feedforward layers, and the order of learnable parameters required for each architecture. The table highlights the trade-offs between different approaches in terms of efficiency and complexity.

In-depth insights

#

ReLU MPNNs

#

The core of this research paper revolves around understanding the functional capabilities of ReLU MPNNs (Rectified Linear Unit Message Passing Neural Networks). The authors leverage tropical geometry to characterize the class of functions these networks can learn, demonstrating an equivalence between ReLU MPNNs, ReLU Feedforward Networks (FNNs), Tropical Rational Signomial Maps (TRSMs), and Continuous Piecewise Linear Maps (CPLMs). This equivalence is a significant finding, as it connects the expressive power of MPNNs to well-established mathematical frameworks. Furthermore, the study delves into the geometric complexity of ReLU MPNNs, providing the first general upper and lower bounds on the number of linear regions these networks can represent. This analysis reveals crucial insights into the impact of architectural choices (aggregation and update functions) on the model’s complexity. Importantly, the research also examines the decision boundaries formed by ReLU MPNNs in node and graph classification tasks, providing a novel perspective on their decision-making process. Overall, this work offers a significant step towards a deeper theoretical understanding of the expressiveness, complexity, and decision boundaries of ReLU MPNNs, bridging the gap between practical implementations and fundamental theoretical limits.

Tropical Geometry

#

The application of tropical geometry to analyze graph neural networks (GNNs) offers a novel perspective. Tropical geometry’s focus on piecewise linear functions aligns well with the ReLU activation functions commonly used in GNNs. This allows researchers to leverage the established mathematical tools of tropical geometry to characterize the class of functions that GNNs can learn. By framing GNN computations within the tropical semiring, the authors gain a powerful framework for understanding and bounding their expressivity. This approach contrasts with the traditional Weisfeiler-Lehman (WL) hierarchy, which primarily focuses on the limitations of GNNs. Instead, tropical geometry helps to reveal the capabilities and complexities of GNNs, such as their geometric complexity (number of linear regions). This is a crucial step towards a deeper understanding of their generalization properties and how architectural choices impact their performance. The theoretical equivalence demonstrated between ReLU GNNs, tropical rational signomial maps, and continuous piecewise linear functions is significant. This equivalence provides valuable insights for designing more efficient and expressive GNN architectures. The ability to transfer knowledge and techniques from tropical geometry to the field of GNNs is promising and opens new avenues for future research.

Expressivity Bounds

#

Expressivity bounds in the context of graph neural networks (GNNs) are crucial for understanding their capabilities and limitations. Tight bounds help determine the class of functions a GNN can learn, which is essential for knowing its potential applications and avoiding overfitting. The Weisfeiler-Lehman (WL) test provides a theoretical framework for assessing GNN expressivity, showing that many GNNs are limited by the 1-WL test. However, practical GNNs often employ non-injective activation functions (like ReLU), making the direct application of the WL test inadequate. Research into expressivity bounds for these practical models often explores alternative approaches, such as using tropical geometry or focusing on the number of linear regions a GNN can distinguish. Establishing lower and upper bounds reveals the fundamental limits of a given GNN architecture, highlighting potential areas for improvement through architectural modifications or by incorporating additional mechanisms. The relationship between depth, width, and the number of parameters is also critical, informing trade-offs in complexity and computational cost. Ultimately, a deeper understanding of expressivity bounds allows for the design of more powerful and efficient GNNs tailored for specific tasks, and provides valuable insights into GNNs’ potential and limitations.

Novel Architectures

#

The research paper explores novel graph neural network (GNN) architectures designed to enhance expressivity and efficiency. The core idea revolves around leveraging the strengths of both feedforward and message-passing paradigms, creating hybrid models. The proposed architectures aim to overcome limitations in existing GNNs by addressing the trade-offs between depth, number of parameters, and computational cost. One key innovation is the introduction of architectures that achieve comparable expressiveness to feedforward networks (FNNs) but with fewer layers and parameters. The theoretical analysis uses tropical geometry to illuminate the underlying mathematical properties of these novel designs and provides crucial insights into their expressiveness. The results suggest that carefully designed architectures can achieve a beneficial balance of model complexity and computational efficiency, paving the way for more powerful and resource-efficient GNN models. A significant contribution is the demonstration of how different aggregation operators (e.g., coordinate-wise max) influence the geometric complexity of the network, offering guidance on architecture design. These findings are expected to shape future research in developing and understanding GNNs, potentially leading to more advanced and scalable models.

Decision Boundary

#

The section on “Decision Boundary” delves into the geometric interpretation of how ReLU MPNNs classify data points. It leverages tropical geometry, establishing a link between the decision boundary and tropical hypersurfaces. This allows for an analysis of the boundary’s structure in terms of the number of connected regions it divides the input space into, relating it to the network’s complexity. The authors characterize the decision boundaries for both node and graph classification tasks, highlighting the differences between the two and providing insights into the underlying mechanisms. The focus on integer-weighted ReLU MPNNs simplifies the analysis, enabling a cleaner connection with the tropical geometric framework. The decision boundary is shown to be contained within a specific tropical hypersurface, thereby connecting the network’s function to the geometric properties of the boundary. This provides a valuable tool for understanding and improving the performance and interpretability of these models.

More visual insights

#

More on figures

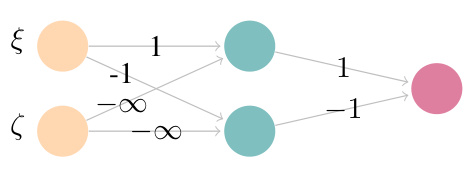
This figure shows two neural network gadgets. The left gadget uses a control input (ζ) to either pass or filter an input (ξ) through the network. The right gadget outputs the maximum of its two inputs.

This figure shows two neural network gadgets used in the paper’s algorithms. The left gadget is a selection gadget that uses a control input to either pass or filter an input value. The right gadget is a comparison gadget that outputs the maximum of two input values.

This figure shows the Broadcast and Selection gadgets used in the paper’s proposed algorithms. The left panel illustrates the Broadcast gadget, which replicates input monomials across nodes in a fully connected graph. The right panel shows the Selection gadget, a neural network that filters these replicated monomials to distribute them evenly among nodes, facilitating efficient comparisons within the algorithms.

Full paper

#