Amortized Eigendecomposition for Neural Networks

↗ arXiv ↗ Hugging Face

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working with neural networks that involve eigendecomposition. It presents a novel, efficient approach that significantly speeds up training while maintaining accuracy, opening up possibilities for new applications of deep learning in areas previously limited by computational constraints. The introduction of the amortized eigendecomposition and its theoretical justifications could inspire new research in optimizing computationally expensive operations within neural networks.

Visual Insights

#

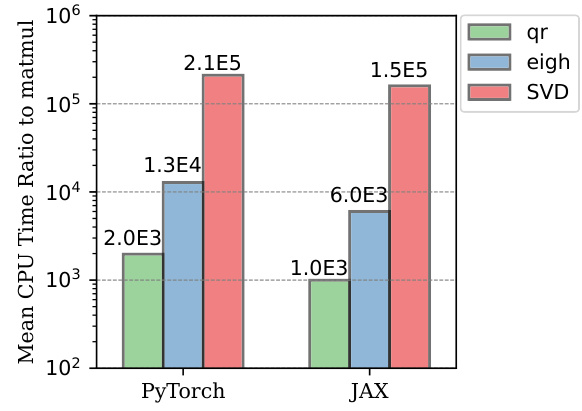
🔼 This figure compares the computation time of QR decomposition, eigenvalue decomposition (eigh), and singular value decomposition (svd) against matrix multiplication. The comparison uses 10000x10000 matrices, with execution times averaged over 100 runs, in PyTorch and JAX. It demonstrates that eigendecomposition and SVD are significantly slower than QR decomposition and matrix multiplication, highlighting a key computational challenge addressed in the paper.

read the caption

Figure 1: A comparison that illustrates the forward execution time of three linear algebra operations: qr, eigh, and svd, when performed on a 10000 × 10000 matrix using PyTorch and JAX. The presented values represent the mean ratios of the execution time relative to that of matrix multiplication (matmul) of 100 runs.

🔼 The table compares the execution time per iteration for three different tasks: nuclear norm regularization, latent-space PCA, and low-rank GCN. For each task, three different backbones are used: a baseline backbone with only reconstruction loss, a backbone with traditional eigendecomposition (eigh/svd), and a backbone using the proposed amortized eigendecomposition method. The table shows the execution times for each backbone (t0, t1, and t2 respectively), as well as the speedup of the amortized eigendecomposition method relative to the traditional method (t1-t0)/(t2-t0). The results demonstrate significant speed improvements using the proposed method.

read the caption

Table 1: Evaluation of execution times per iteration on three tasks.

In-depth insights

#

Amortized Eigen-Decomp

#

Amortized eigendecomposition offers a novel approach to address the computational bottleneck of traditional eigendecomposition methods within neural network training. By introducing an additional loss term, the eigen loss, it relaxes the requirement for exact eigendecomposition, replacing it with more computationally efficient QR decomposition at each iteration. This significantly accelerates training while maintaining accuracy. The theoretical analysis demonstrates that the desired eigenpairs are obtained as optima of the eigen loss. Empirical studies across various applications, including nuclear norm regularization, latent-space PCA, and graph adversarial learning, showcase substantial improvements in training efficiency without sacrificing the quality of results. The amortized approach efficiently integrates eigendecomposition into the neural network training process, overcoming computational limitations and unlocking new potential for advanced deep learning applications. This technique provides a valuable alternative for situations where traditional methods prove computationally prohibitive.

Neural Eigen-Loss

#

A neural eigen-loss would represent a novel approach to integrate eigendecomposition directly into the neural network training process. Unlike traditional methods that decouple eigendecomposition as a separate pre- or post-processing step, a neural eigen-loss would embed the eigen-objective as part of the main loss function. This would likely involve representing eigenvectors using a differentiable parameterization, such as QR decomposition, and defining a loss that penalizes deviations from the desired eigen-properties. This approach offers several potential advantages: increased training efficiency by avoiding the computationally expensive iterative methods used in standard eigendecomposition, smoother optimization dynamics via gradient-based methods, and seamless integration with automatic differentiation tools. However, there are potential challenges. Designing an effective and numerically stable neural eigen-loss requires careful consideration: the choice of parameterization significantly affects the optimization landscape, potential issues with gradient vanishing/exploding in deep networks, and the need to ensure that the optimization process reliably converges to the true eigenvectors. Moreover, the impact of the eigen-loss on overall network training stability requires comprehensive empirical analysis. Theoretical analysis of the loss function’s properties, particularly concerning convergence guarantees and optimization efficiency, is also crucial. Successful implementation would lead to novel neural network architectures capable of efficiently leveraging spectral information and potentially opening doors to new applications such as improved spectral graph neural networks and fast, efficient low-rank approximations.

Convergence Analysis

#

A convergence analysis in a machine learning context typically evaluates how quickly and accurately a model’s parameters approach their optimal values during training. It often involves examining the model’s loss function over iterations. Key aspects include the rate of convergence (linear, superlinear, etc.), the impact of hyperparameters on the speed and stability of convergence, and the final level of accuracy achieved. Analyzing convergence curves (plots of loss versus iterations) helps to identify potential issues like slow convergence, oscillations, or premature halting. Theoretical guarantees on convergence are highly valued, but often depend on specific assumptions about the model and data. Empirical experiments using various optimization algorithms (e.g., SGD, Adam) are crucial for validating convergence behavior in practice and demonstrating its robustness under various conditions. Different metrics beyond loss functions (e.g., accuracy, precision, recall) might be utilized to assess convergence depending on the specific task. A comprehensive convergence analysis is essential for understanding a model’s learning dynamics and its performance capabilities.

Computational Speedup

#

This research paper focuses on accelerating eigendecomposition within neural network training. A core challenge is the significant computational cost of standard eigendecomposition algorithms, which slows down training. The proposed solution, amortized eigendecomposition, replaces the expensive eigendecomposition with a more affordable QR decomposition, significantly improving speed. This is achieved by introducing an additional loss term called ’eigen loss’, which guides the QR decomposition towards the desired eigenpairs. Empirical results demonstrate substantial speed improvements across various applications, including nuclear norm regularization, latent-space PCA, and graph adversarial training, with minimal impact on accuracy. The key innovation lies in realizing that exact eigendecomposition at every training iteration is unnecessary, and that a less computationally intensive approximation suffices. This represents a substantial breakthrough in integrating eigendecomposition into deep learning, previously hindered by its high computational demands. The paper provides strong theoretical justification for the approach and a thorough empirical validation.

Future Research

#

Future research directions stemming from this amortized eigendecomposition method could explore several promising avenues. Extending the approach to handle complex matrices and non-symmetric matrices is crucial for broader applicability in various deep learning tasks. Investigating the impact of different regularization techniques and loss functions on the accuracy and efficiency of the method warrants further study. A thorough analysis of the method’s scalability to extremely large-scale datasets and networks is necessary to assess its practical viability for real-world applications. Moreover, combining this technique with other optimization strategies, such as adaptive gradient methods, could lead to even greater efficiency gains. Finally, exploring applications in domains beyond those examined in this paper, such as reinforcement learning and graph neural networks, would unveil the full potential of this novel approach to eigendecomposition in neural network training.

More visual insights

#

More on figures

🔼 This figure compares three different loss functions for finding eigenvectors of a 2D symmetric matrix. It shows how the trace loss suffers from rotational symmetry, leading to many optimal solutions, while Brockett’s cost function and a convex trace loss break this symmetry and yield unique optima corresponding to the true eigenvectors. The plots illustrate the loss function landscapes with contour lines, highlighting the optimal points (red stars).

read the caption

Figure 2: An illustration on disrupting the rotational symmetry of the trace loss. We aim to solve eigenvectors for a 2-dimensional symmetric matrix A = \begin{pmatrix} 0.3 & 0.2\\ 0.2 & 0.1 \end{pmatrix}, with three loss functions. We parameterize an orthonormal matrix U = \begin{pmatrix} x\\ y \end{pmatrix} subject to the constraint x² + y² = 1. The plot displays the contours of the landscapes of three different loss functions as they vary with x and y: (a) trace loss tr(UAUT), (b) Brockett's cost function tr(MUAUT) where M = diag(1,0.2) and (c) convex loss function tr(f(U AUT)) where f is an element-wise exponential function. The feasible area of the constraint is depicted with a black circle. The red stars signify the optima of the loss in the feasible area. The dashed grey lines represent the true eigenvector direction of A. We see that, the trace loss results in infinitely many optimal solutions due to its rotational symmetry. In contrast, both Brockett's cost function and the convex loss function reshape the optimization landscape, breaking this symmetry and leading to the identification of the correct eigenvectors.

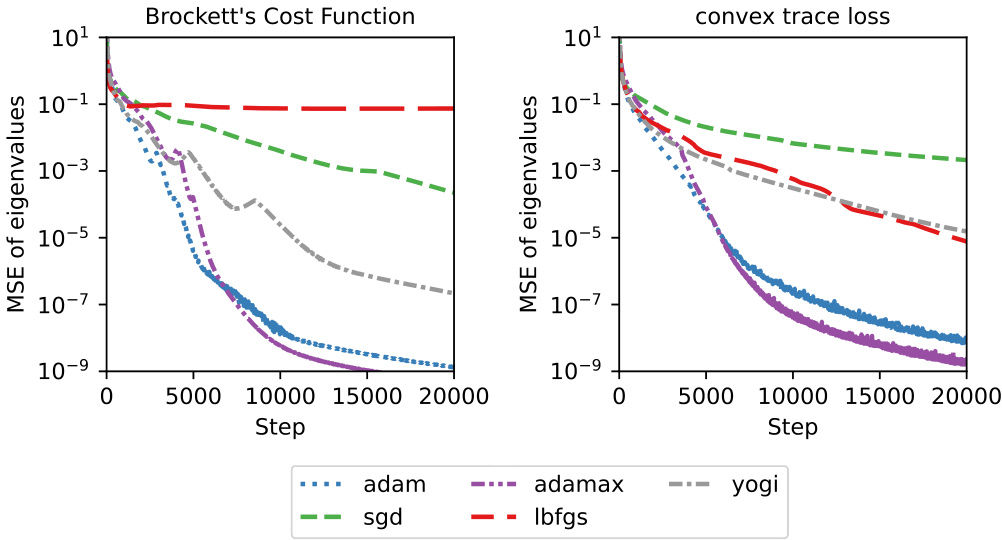
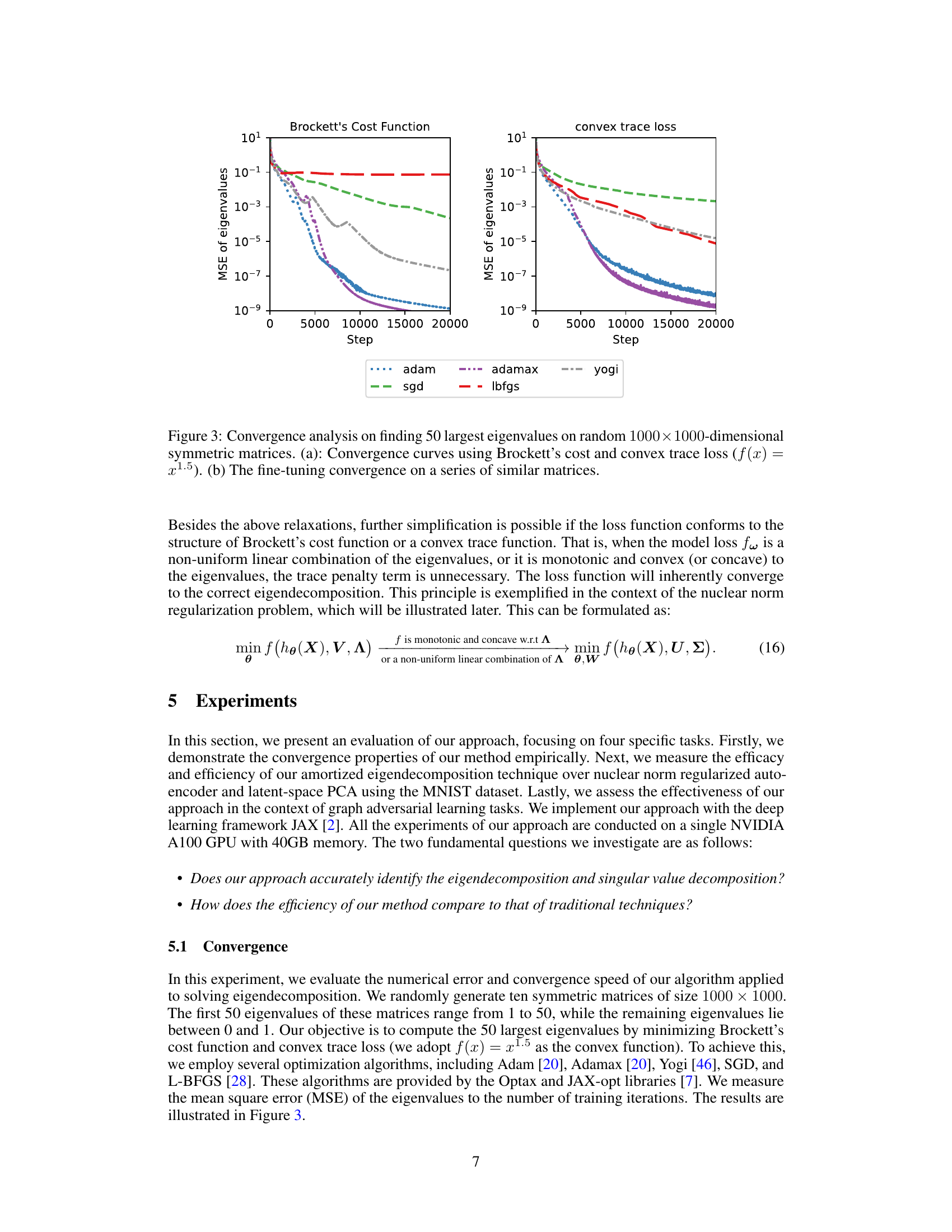
🔼 This figure shows the convergence speed and accuracy of different optimization algorithms in finding the top 50 eigenvalues of random 1000x1000 symmetric matrices using two different loss functions: Brockett’s cost function and a convex trace loss function. Subfigure (a) compares the convergence curves of various optimizers (Adam, Adamax, Yogi, SGD, L-BFGS) for both loss functions. Subfigure (b) demonstrates the fine-tuning capability of the approach on a sequence of similar matrices, highlighting the stability and robustness of the method.

read the caption

Figure 3: Convergence analysis on finding 50 largest eigenvalues on random 1000×1000-dimensional symmetric matrices. (a): Convergence curves using Brockett’s cost and convex trace loss (f(x) = x1.5). (b) The fine-tuning convergence on a series of similar matrices.

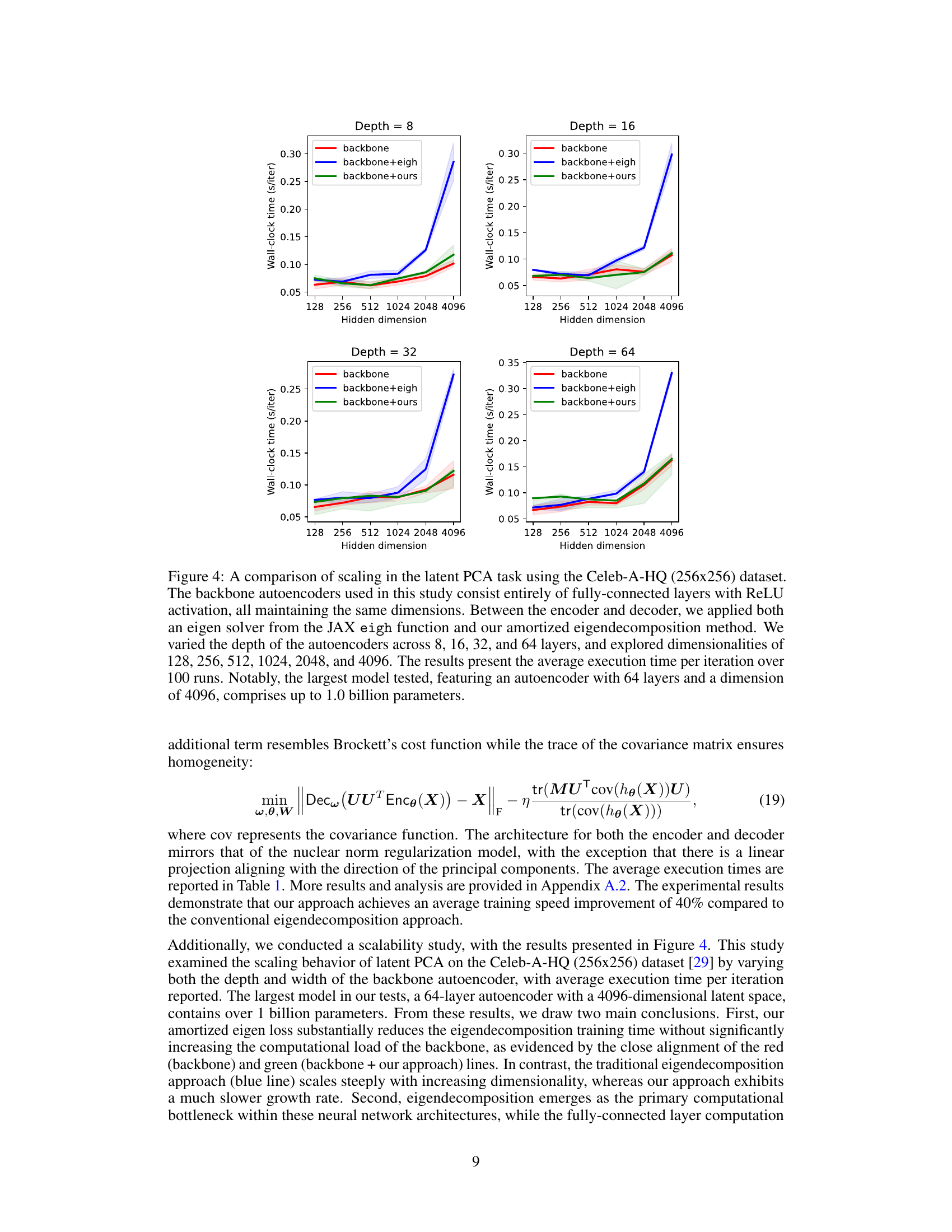
🔼 This figure compares the performance of different autoencoder architectures in a latent PCA task using the Celeb-A-HQ dataset. It shows the wall-clock time per iteration for various hidden dimensions and depths of the autoencoder. The comparison includes a baseline autoencoder, one with JAX’s eigh function for eigendecomposition, and one using the proposed amortized eigendecomposition method. The results highlight the significant speedup achieved by the proposed method, particularly for larger and deeper models.

read the caption

Figure 4: A comparison of scaling in the latent PCA task using the Celeb-A-HQ (256x256) dataset. The backbone autoencoders used in this study consist entirely of fully-connected layers with ReLU activation, all maintaining the same dimensions. Between the encoder and decoder, we applied both an eigen solver from the JAX eigh function and our amortized eigendecomposition method. We varied the depth of the autoencoders across 8, 16, 32, and 64 layers, and explored dimensionalities of 128, 256, 512, 1024, 2048, and 4096. The results present the average execution time per iteration over 100 runs. Notably, the largest model tested, featuring an autoencoder with 64 layers and a dimension of 4096, comprises up to 1.0 billion parameters.

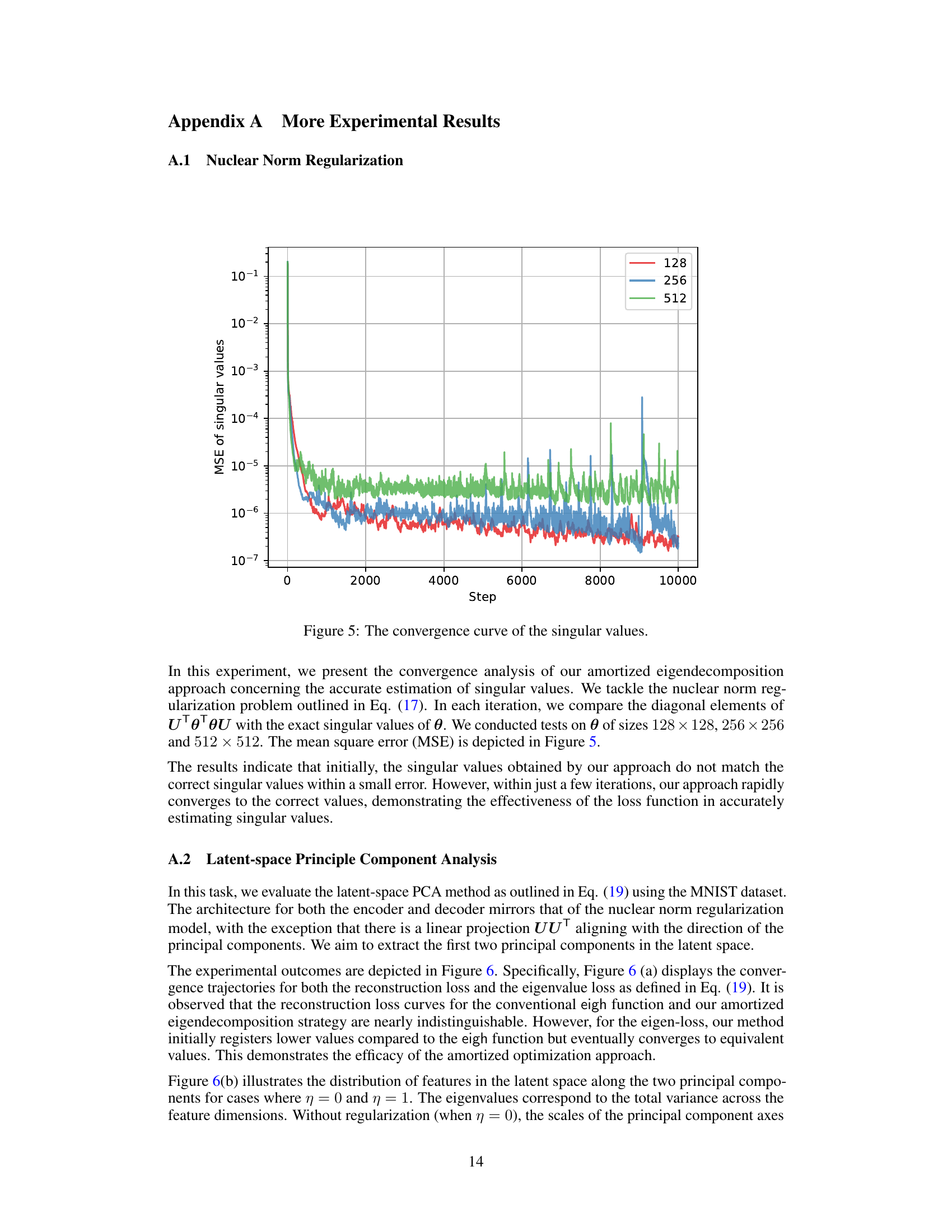
🔼 This figure shows the convergence analysis of the amortized eigendecomposition approach for estimating singular values in the nuclear norm regularization problem. Three different hidden layer dimensions (128, 256, and 512) are used, and the mean squared error (MSE) between the estimated singular values and the exact singular values is plotted against the number of training steps. The results demonstrate that the method converges rapidly to the exact singular values, even with high dimensionality.

read the caption

Figure 5: The convergence curve of the singular values.

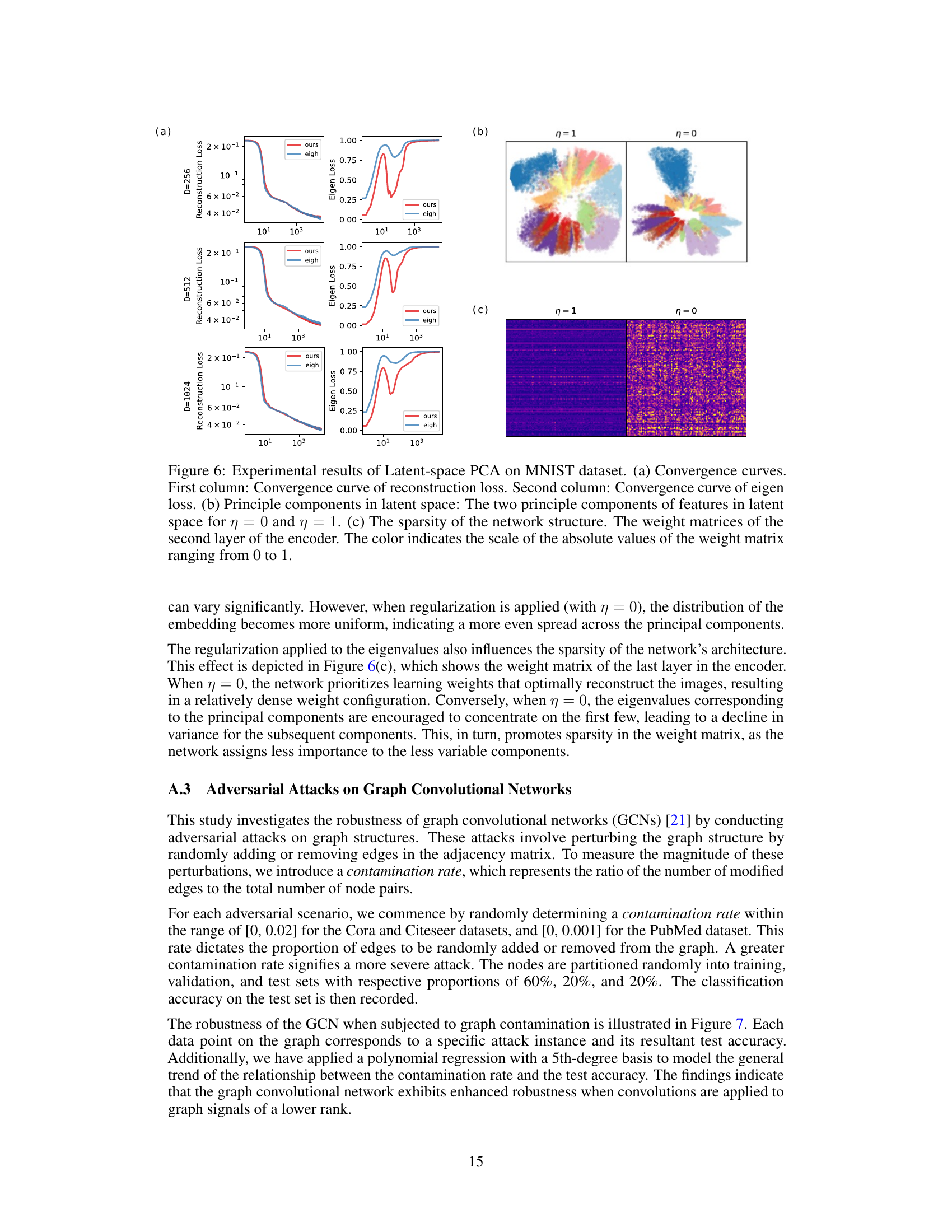
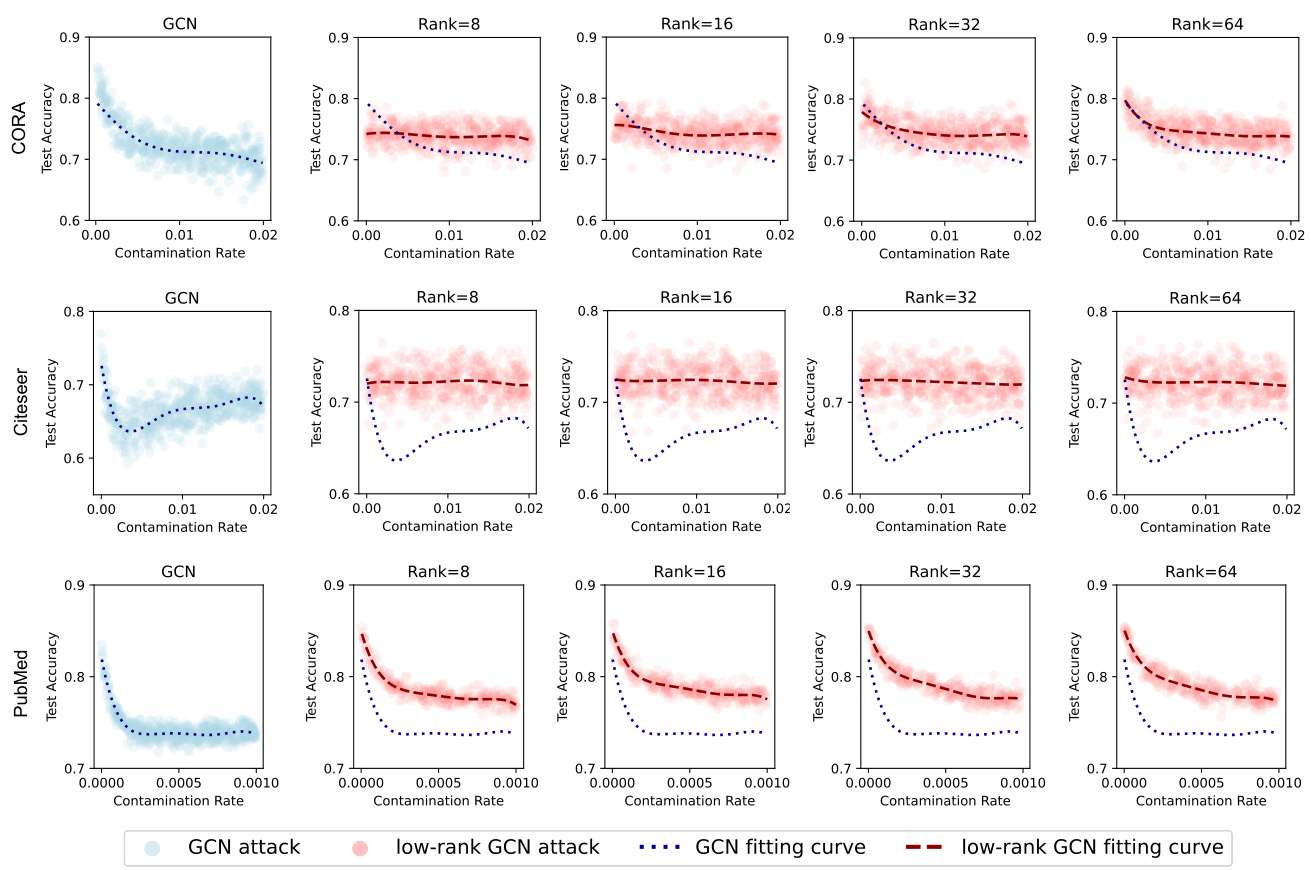
🔼 This figure presents the experimental results of the Latent-space Principle Component Analysis (PCA) on the MNIST dataset. It shows the convergence of both reconstruction and eigen losses for different hidden dimensions (256, 512, 1024). The visualization of the latent space, with two principle components, for both regularized (η=1) and unregularized (η=0) cases, illustrates the effect of regularization. Finally, the sparsity of the network weight matrices (second layer of the encoder) is shown, highlighting the differences in sparsity between regularized and unregularized scenarios.

read the caption

Figure 6: Experimental results of Latent-space PCA on MNIST dataset. (a) Convergence curves. First column: Convergence curve of reconstruction loss. Second column: Convergence curve of eigen loss. (b) Principle components in latent space: The two principle components of features in latent space for η = 0 and η = 1. (c) The sparsity of the network structure. The weight matrices of the second layer of the encoder. The color indicates the scale of the absolute values of the weight matrix ranging from 0 to 1.

🔼 This figure shows the convergence analysis of the proposed amortized eigendecomposition approach in finding eigenvalues. Subfigure (a) presents convergence curves for Brockett’s cost function and a convex trace loss function using several optimization algorithms (Adam, Adamax, Yogi, SGD, and L-BFGS). Subfigure (b) demonstrates the fine-tuning convergence behavior on a series of similar matrices, further highlighting the robustness and efficiency of the approach. The results illustrate that the method accurately and efficiently finds the eigenvalues even with fine-tuning on similar matrices.

read the caption

Figure 3: Convergence analysis on finding 50 largest eigenvalues on random 1000 × 1000-dimensional symmetric matrices. (a): Convergence curves using Brockett’s cost and convex trace loss (f(x) = x1.5). (b) The fine-tuning convergence on a series of similar matrices.

Full paper

#