↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Vector Symbolic Architectures (VSAs) are used in neuro-symbolic AI to perform symbolic manipulations on vectors, but existing VSAs face issues with computational complexity or numerical stability. Many VSAs were designed before deep learning became popular and thus do not easily integrate with modern deep learning systems. This limits their use in various applications.
This paper introduces the Hadamard-derived Linear Binding (HLB), a novel VSA designed for improved computational efficiency and numerical stability. HLB uses the Walsh Hadamard transform to achieve linear time complexity, avoiding the O(d log d) complexity associated with the Fourier transform used in other VSAs. Experimental results show that HLB outperforms or matches existing VSAs in both classical VSA tasks and in deep-learning applications, such as extreme multi-label classification and a cryptographic privacy application. HLB is shown to be numerically stable and shows advantages in both classical and recent deep learning tasks.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel and efficient vector symbolic architecture, HLB, that offers improvements over existing methods in both classical and deep-learning applications. Its linear time complexity and numerical stability make it particularly attractive for resource-constrained environments and large-scale applications. The research opens up new avenues for integrating symbolic and sub-symbolic AI, a crucial area of current research.
Visual Insights#
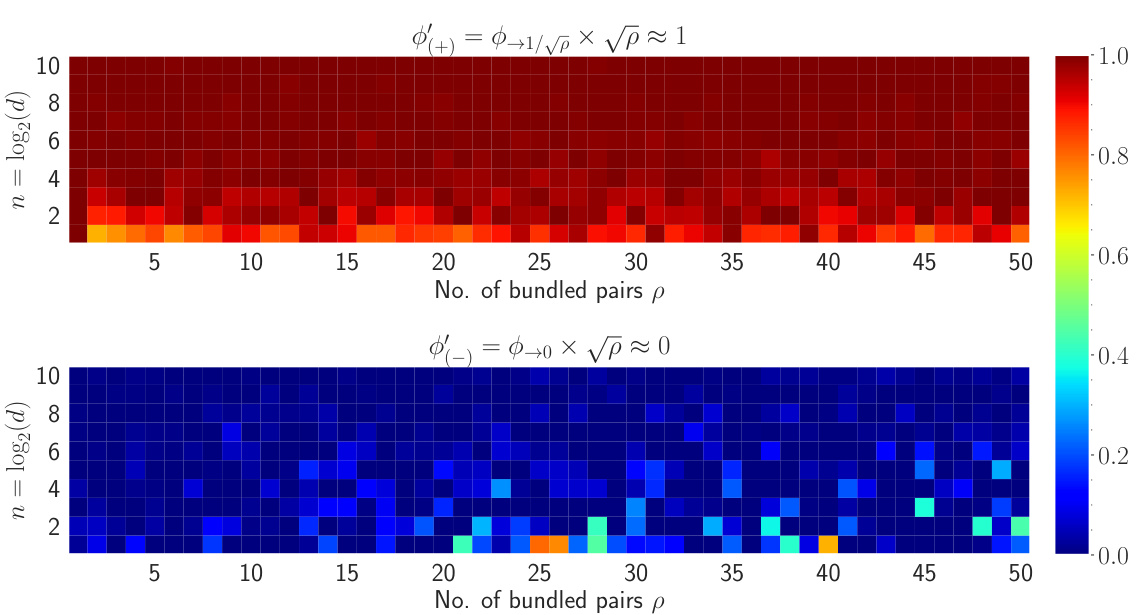
This figure shows the results of an empirical study that compares the corrected cosine similarity scores ($ \phi^{(+)}\text{ and }\phi^{(-)}$) for different numbers of vector pairs (p) and dimensions (d=2^n). The heatmaps show that the corrected cosine similarity for positive cases ($ \phi^{(+)}$) is close to 1, and for negative cases ($ \phi^{(-)}$) is close to 0. This indicates the effectiveness of the proposed method in accurately identifying whether a vector has been bound to a VSA or not when the number of bundled vector pairs is known.
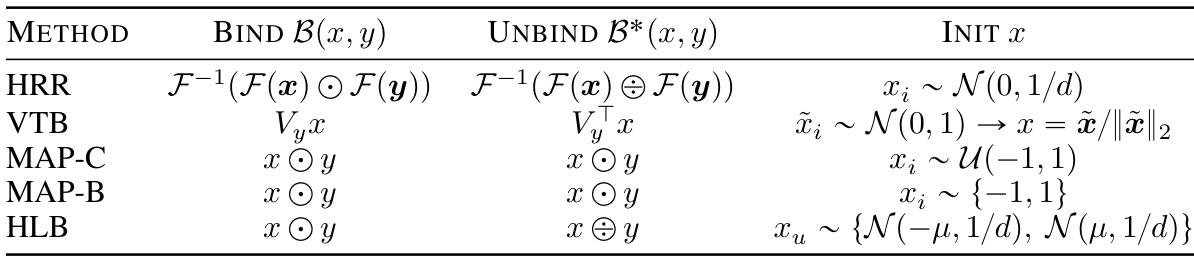
This table summarizes the binding and unbinding operations, as well as the vector initialization for five different vector symbolic architectures (VSAs): HRR, VTB, MAP-C, MAP-B, and the novel HLB method proposed in the paper. It highlights the key differences in their mathematical formulations and how these differences affect their computational efficiency and performance. The table shows that the HLB method is related to the HRR, but uses the Hadamard transform instead of the Fourier transform, leading to simplification. While MAP has a similar structure, the difference in the unbinding operation greatly impacts the performance. The VTB is presented as a recently developed state-of-the-art method for comparison.
In-depth insights#
Hadamard Binding#
Hadamard binding, a novel approach in vector symbolic architectures (VSAs), leverages the Hadamard transform for efficient and numerically stable binding and unbinding operations. Its key advantage lies in its O(d) time complexity, a significant improvement over other VSAs that often scale with O(d log d) or O(d²). This efficiency is achieved by replacing the computationally expensive Fourier transform, commonly used in holographic reduced representations (HRRs), with the Hadamard transform, simplifying calculations while maintaining desirable properties like associativity and commutativity. The method’s numerical stability stems from the use of only +1 and -1 values in the Hadamard matrix, mitigating the potential instability issues associated with the Fourier transform. The introduction of a projection step further enhances accuracy by reducing noise accumulation, a critical factor in maintaining the fidelity of symbolic manipulations within VSAs. Empirical results demonstrate its competitive performance against existing VSAs on classical benchmark tasks and shows promise in deep learning applications. Overall, Hadamard binding presents a compelling alternative in VSAs, combining computational efficiency and numerical robustness.
VSA Deep Learning#
The integration of Vector Symbolic Architectures (VSAs) with deep learning is a promising area of research, aiming to bridge the gap between symbolic reasoning and connectionist learning. VSAs offer unique advantages for representing and manipulating symbolic information within a vector space, allowing for neuro-symbolic AI. Key challenges lie in efficiently integrating VSAs into the differentiable framework of deep learning, addressing potential numerical stability issues, and achieving competitive performance compared to purely connectionist approaches. Promising directions include exploring various VSA binding operations within differentiable neural networks, developing novel loss functions tailored to the VSA representation, and investigating their application to tasks like knowledge representation and reasoning, natural language processing, and robot control. Successful integration would likely require a careful consideration of the computational complexity of VSA operations and finding ways to improve their numerical stability within deep learning models. The ultimate goal is to create hybrid systems that leverage the strengths of both VSAs and deep learning, leading to more robust, explainable, and powerful AI systems.
HLB Advantages#
The Hadamard-derived Linear Binding (HLB) offers several key advantages. Computational efficiency is a major plus, boasting O(d) complexity for binding, a significant improvement over other VSAs. This efficiency stems from its use of the Hadamard transform, avoiding the O(d log d) complexity of Fourier-based methods. Numerical stability is another benefit, as HLB utilizes only {-1, 1} values, preventing the instability issues associated with irrational numbers in Fourier transforms. Performance in classic VSA tasks and deep learning applications is comparable to or surpasses existing methods such as HRR and VTB, demonstrating its effectiveness across various domains. Furthermore, theoretical properties of HLB make it a strong choice; it maintains neuro-symbolic properties while achieving linear time complexity. Simple gradient calculations contribute to its success in deep learning applications. The improved noise handling further enhances its robustness and accuracy.
Classic VSA Tasks#
The section on “Classic VSA Tasks” evaluates the performance of the novel Hadamard-derived Linear Binding (HLB) architecture against existing Vector Symbolic Architectures (VSAs) on established benchmark tasks. The focus is on accuracy in retrieving bound vectors, a core functionality of VSAs. The experimental setup involves creating bundles of vector pairs and then testing the ability of each VSA to correctly retrieve a specific vector given its paired vector and the bundle. HLB demonstrates comparable performance to state-of-the-art methods, such as the Holographic Reduced Representation (HRR) and Vector-Derived Transformation Binding (VTB), significantly outperforming simpler methods like Multiply-Add-Permute (MAP). This comparison provides a strong validation of HLB’s effectiveness in handling fundamental VSA operations, highlighting its potential for broader neuro-symbolic applications.
Future of HLB#
The Hadamard-derived Linear Binding (HLB) method shows considerable promise for neuro-symbolic AI. Its linear time complexity and numerical stability, unlike some previous methods, are key advantages. Future work could explore HLB’s applications in more complex tasks such as reasoning and planning, potentially combining it with advanced deep learning architectures. Extending HLB to handle variable-length sequences efficiently, is also crucial. Further investigation into the theoretical properties of HLB, especially concerning noise accumulation in large-scale bindings, warrants further research. Exploring different initialization strategies beyond the Mixture of Normal Distribution (MiND) could improve performance and robustness. Finally, the development of efficient hardware implementations of HLB would be highly beneficial for real-world applications requiring low-latency processing.
More visual insights#
More on figures
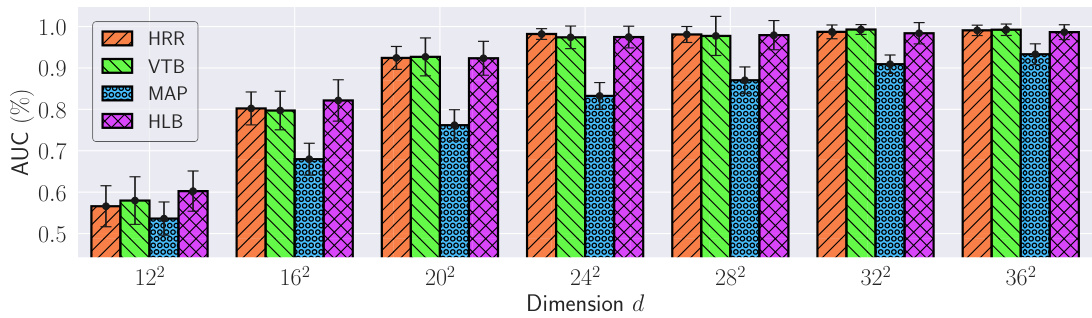
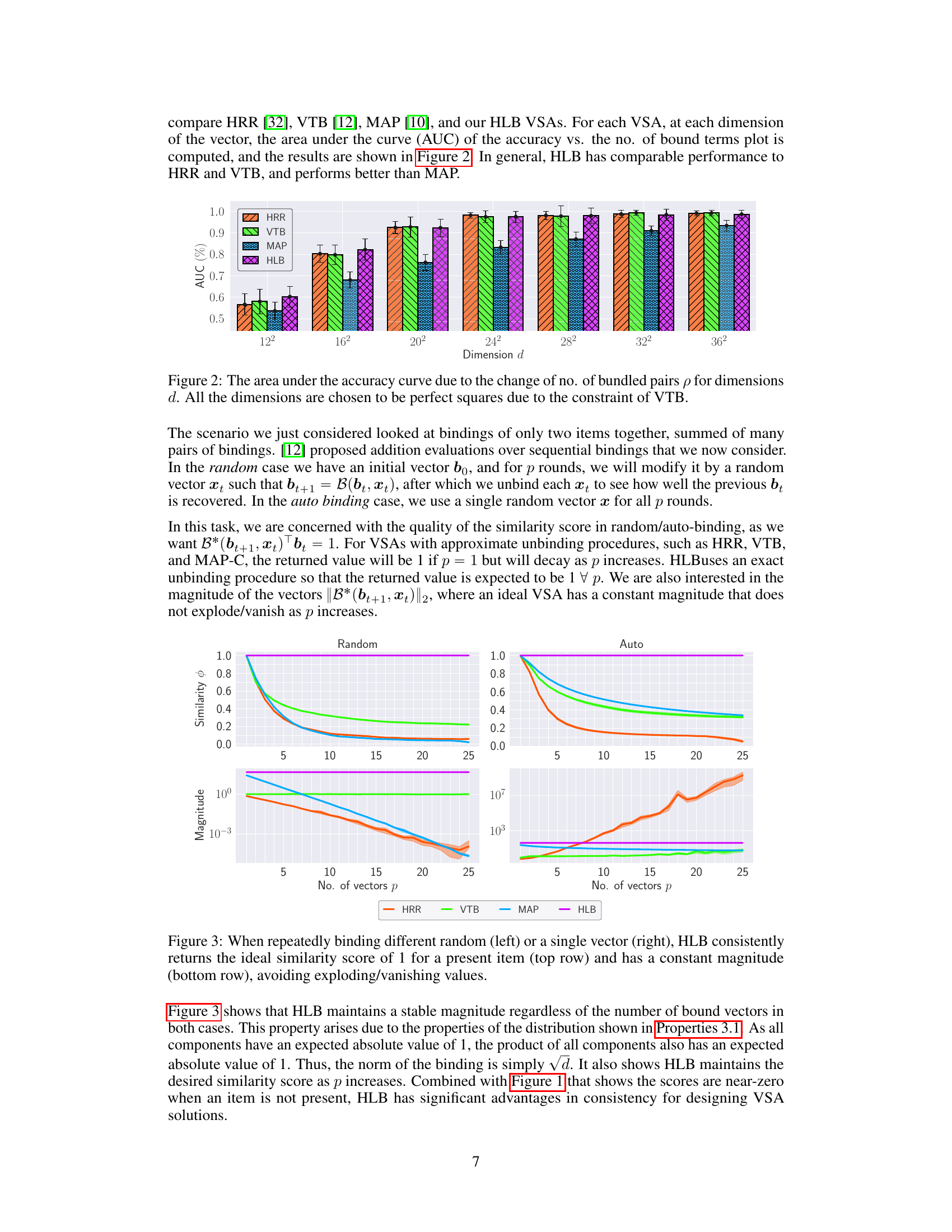
This figure shows the area under the curve (AUC) of the accuracy versus the number of bundled pairs for different vector dimensions (d). It compares the performance of four different Vector Symbolic Architectures (VSAs): HRR, VTB, MAP, and the proposed HLB. The dimensions are chosen as perfect squares to accommodate the requirements of the VTB method. The AUC provides a summary measure of each VSA’s performance across various numbers of bundled vector pairs.
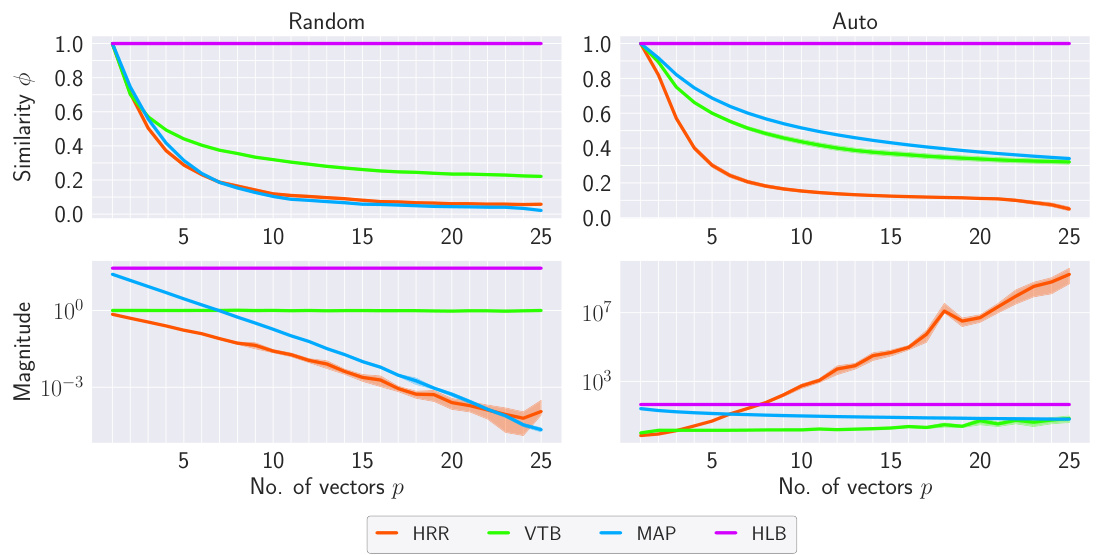
This figure shows the results of an experiment where different VSAs (HRR, VTB, MAP, and HLB) were repeatedly used to bind either a different random vector or a single vector in each round. The top row shows the similarity score between the original vector and the retrieved vector. The bottom row shows the magnitude of the retrieved vector. The figure demonstrates that HLB consistently maintains a similarity score close to 1 and a constant magnitude, even with a large number of repeated bindings. This contrasts with the other VSAs, which show a decline in similarity and/or instability in magnitude as the number of bindings increases. This indicates that HLB is more robust and reliable for tasks involving repeated binding operations.
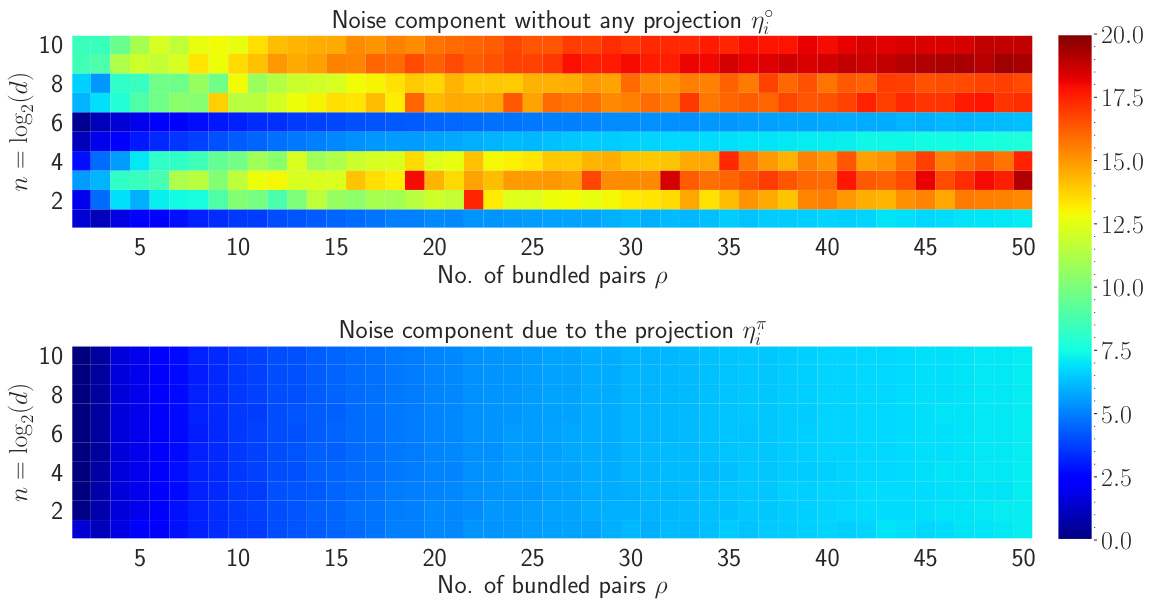
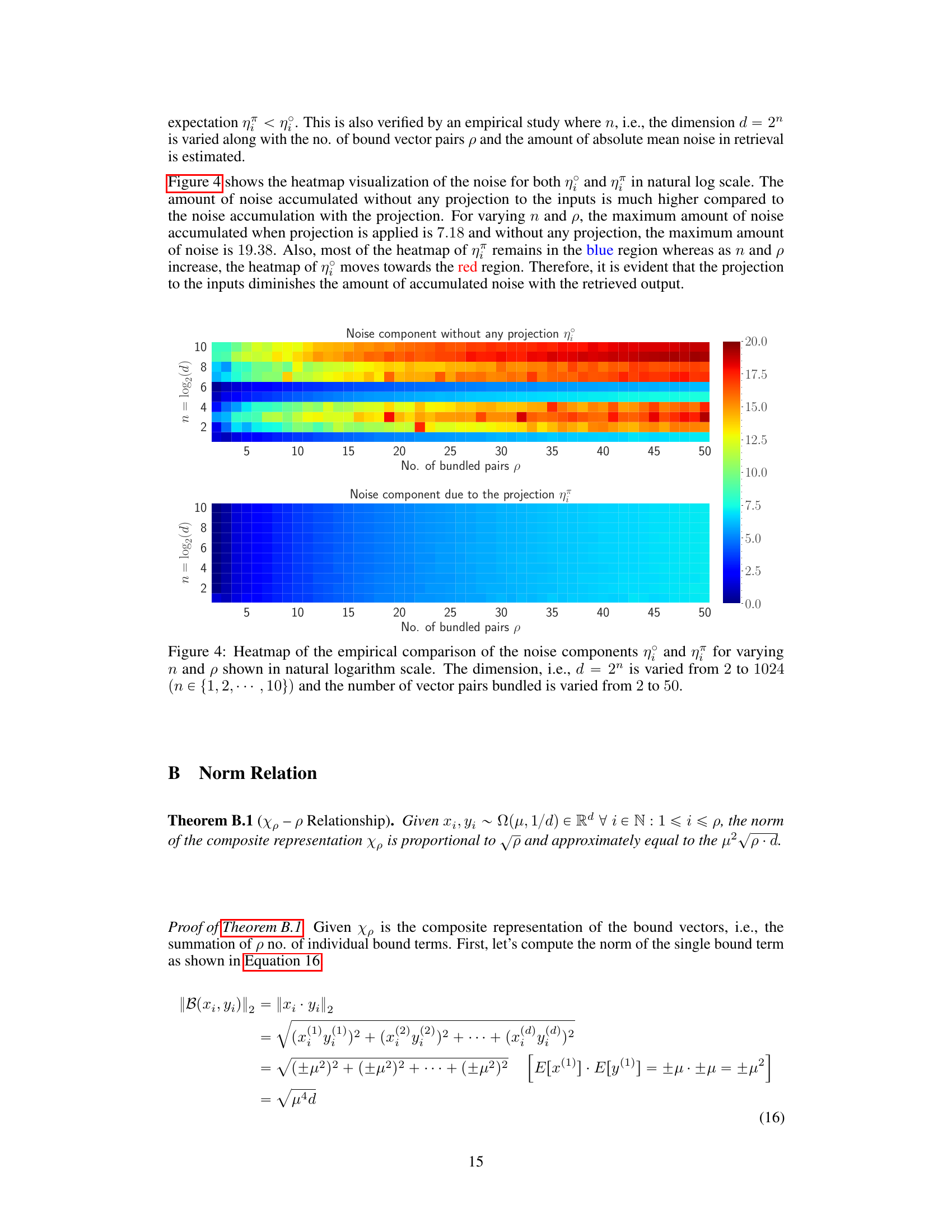
This figure shows the heatmap visualization of the noise for both η and η in natural log scale. The amount of noise accumulated without any projection to the inputs is much higher compared to the noise accumulation with the projection. For varying n and p, the maximum amount of noise accumulated when projection is applied is 7.18 and without any projection, the maximum amount of noise is 19.38. Also, most of the heatmap of η remains in the blue region whereas as n and p increase, the heatmap of η moves towards the red region. Therefore, it is evident that the projection to the inputs diminishes the amount of accumulated noise with the retrieved output.
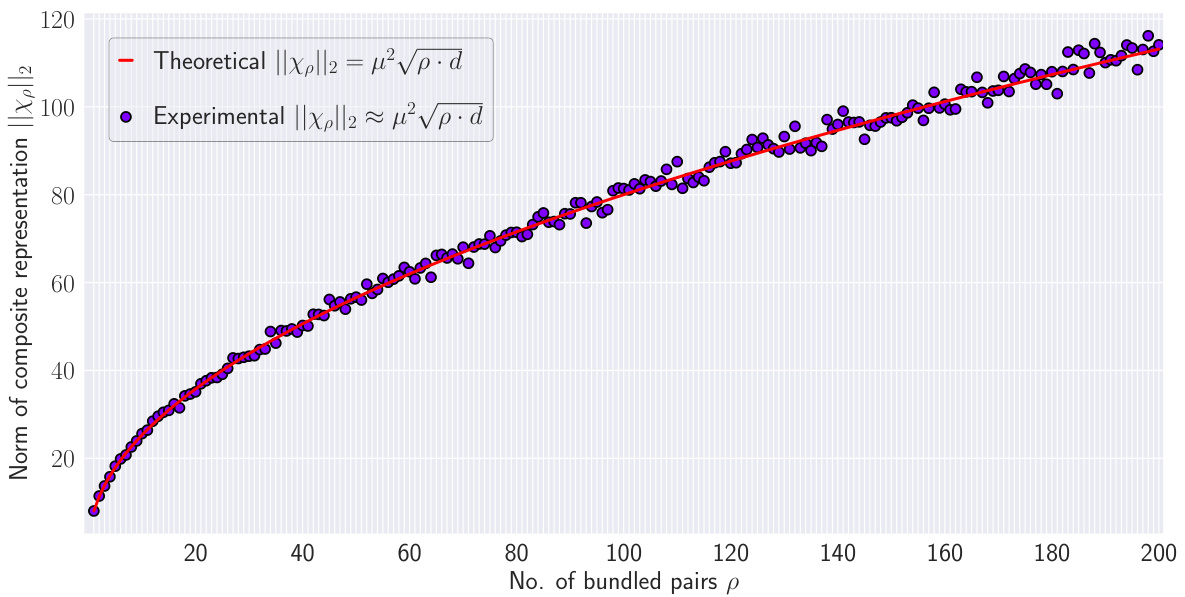
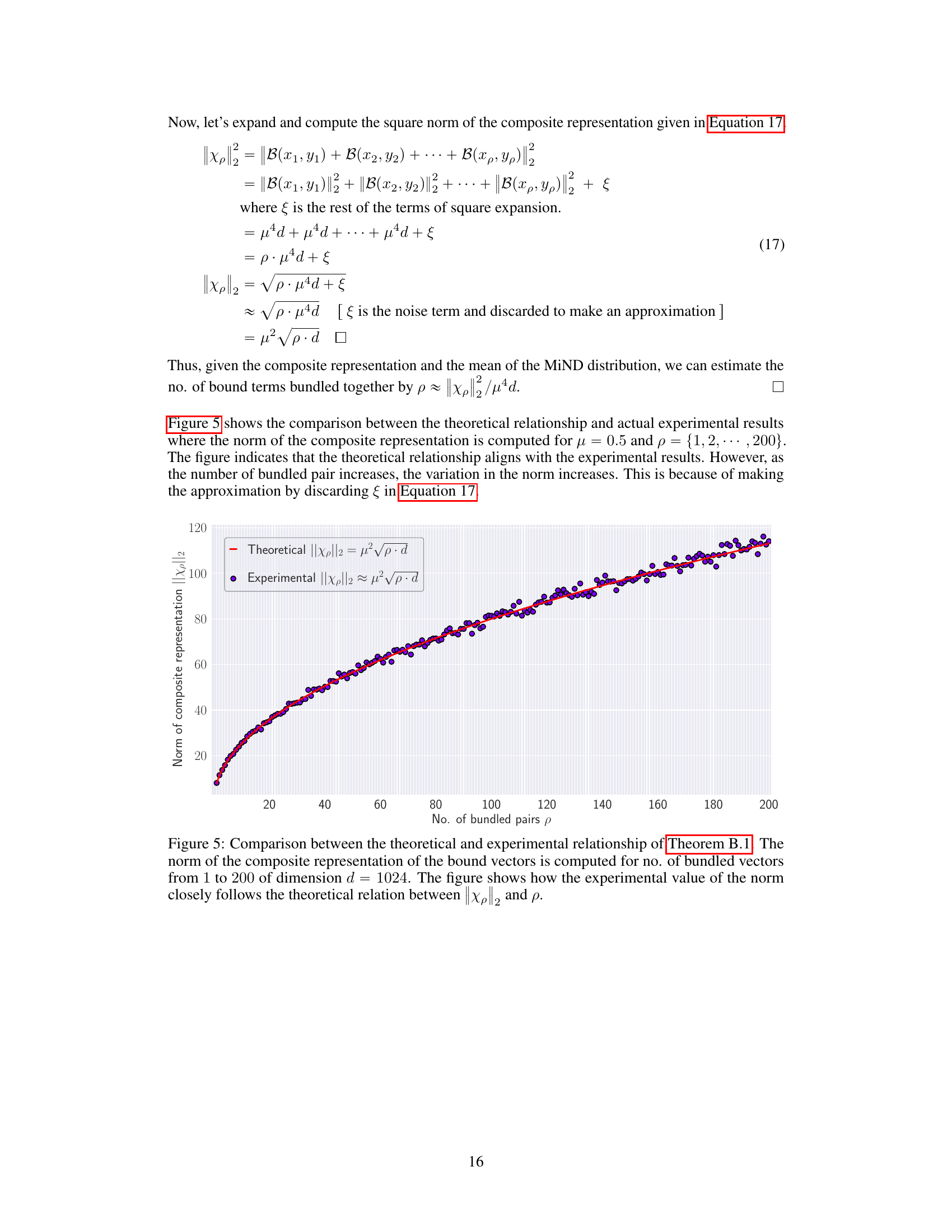
This figure empirically validates Theorem B.1, which states that the norm of the composite representation (||Xp||2) is proportional to the square root of the number of bundled vector pairs (√p). The graph plots the theoretical norm (red line) against the experimentally obtained norm (purple dots) for 200 bundled pairs of vectors in a 1024-dimensional space. The close agreement between the theoretical prediction and experimental results supports the theorem, showing that the approximation holds well even for a substantial number of bound vectors. Slight deviations are observed, particularly at higher values of p, likely due to the approximation made in the theorem’s derivation (discarding noise terms).
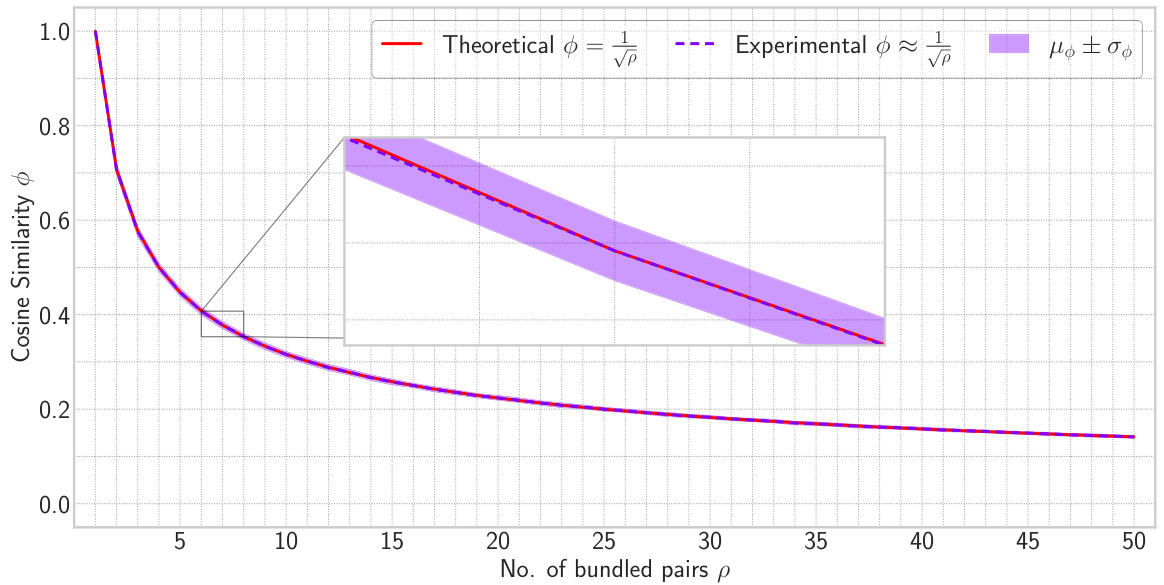
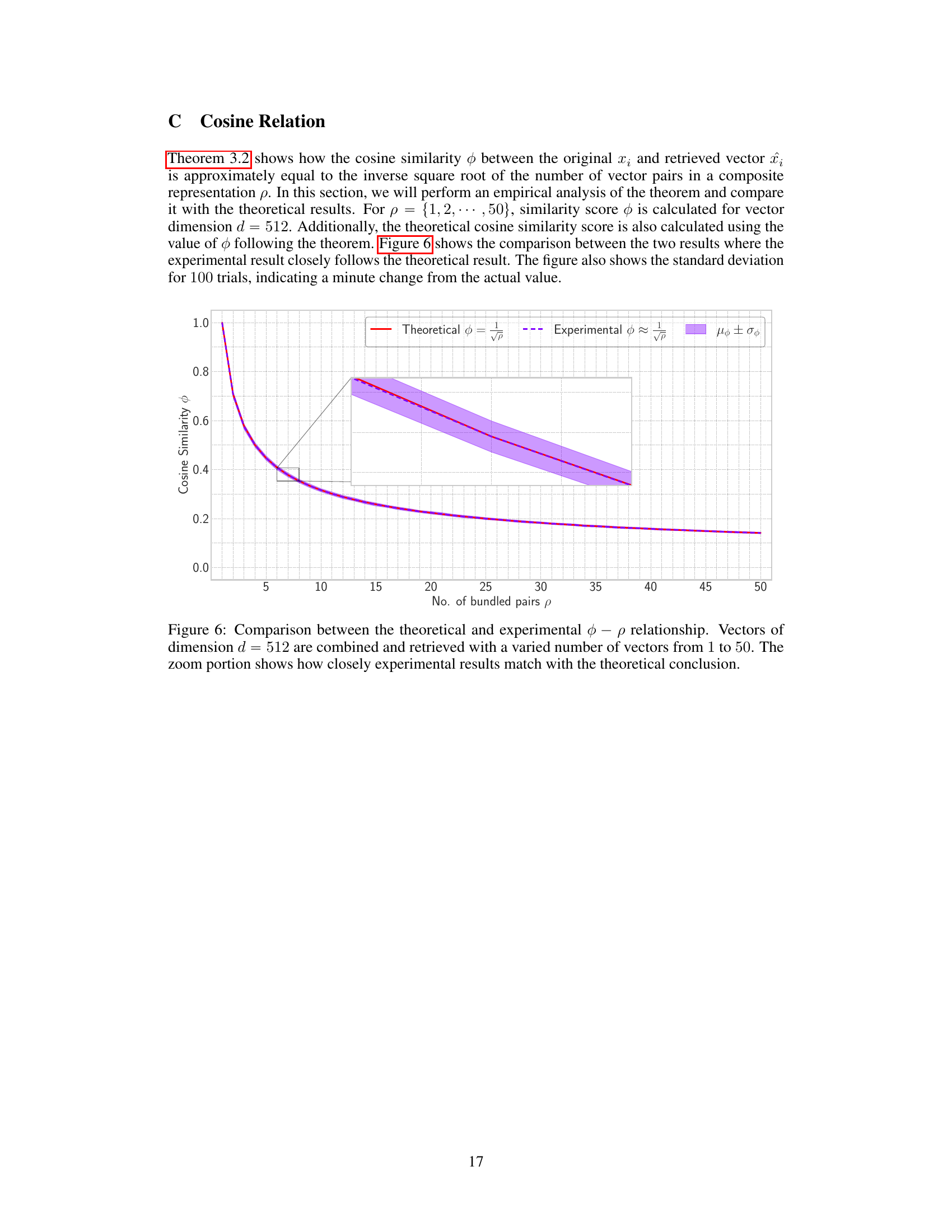
This figure compares the theoretical and experimental results of the relationship between cosine similarity (φ) and the number of bundled pairs (p). The theoretical relationship, derived from Theorem 3.2, predicts that cosine similarity decreases proportionally to the inverse square root of the number of bundled pairs. The experimental results, obtained through simulations, closely follow the theoretical prediction, with the shaded region showing the standard deviation. The zoomed inset highlights the close agreement between theoretical and experimental values.
More on tables
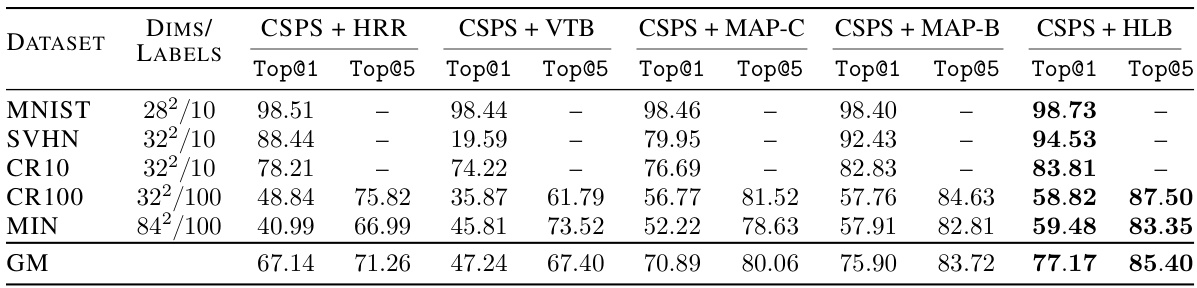
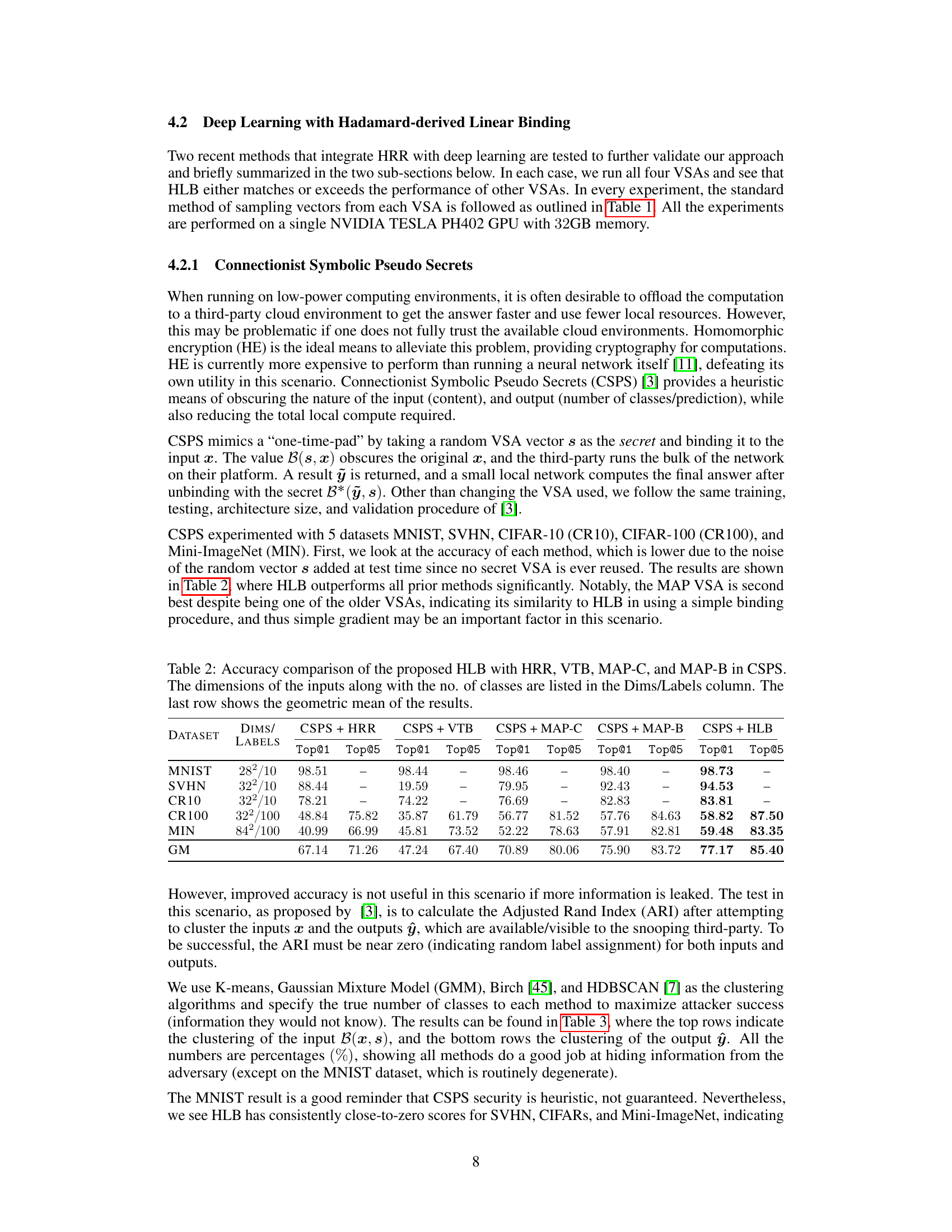
This table compares the accuracy of five different VSAs (HLB, HRR, VTB, MAP-C, and MAP-B) on five different datasets (MNIST, SVHN, CR10, CR100, and MIN) when used within the Connectionist Symbolic Pseudo Secrets (CSPS) framework. The accuracy is measured using Top@1 and Top@5 metrics, representing the percentage of times the correct class is ranked within the top 1 and top 5 predictions respectively. The geometric mean (GM) across all datasets and metrics is also calculated and shown in the last row for comparison.
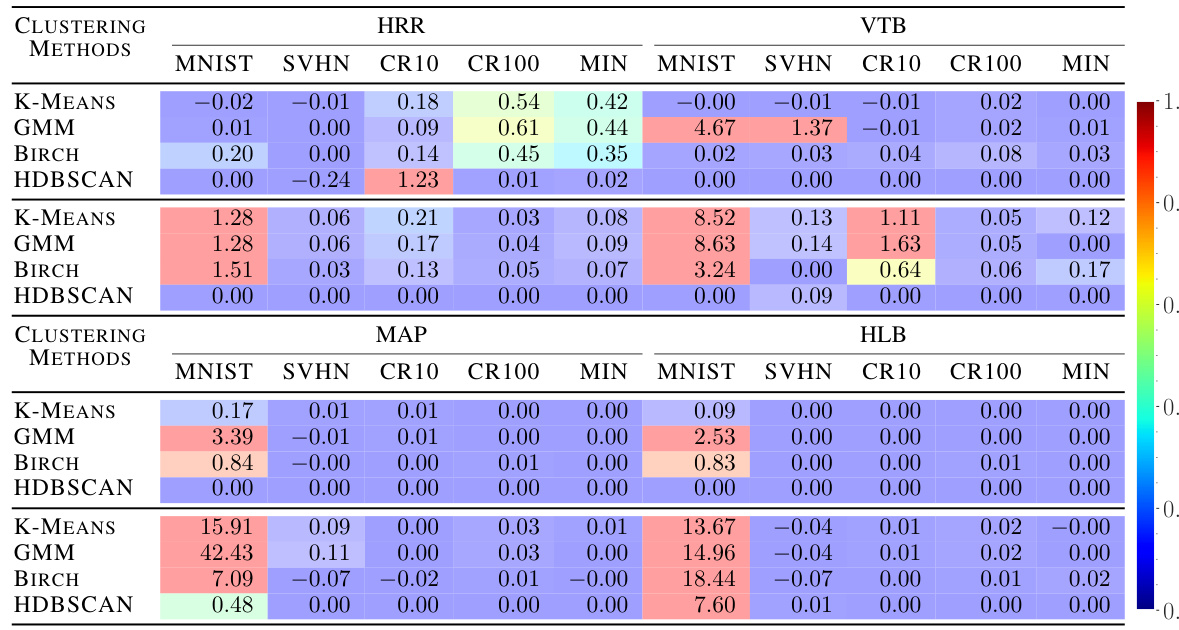
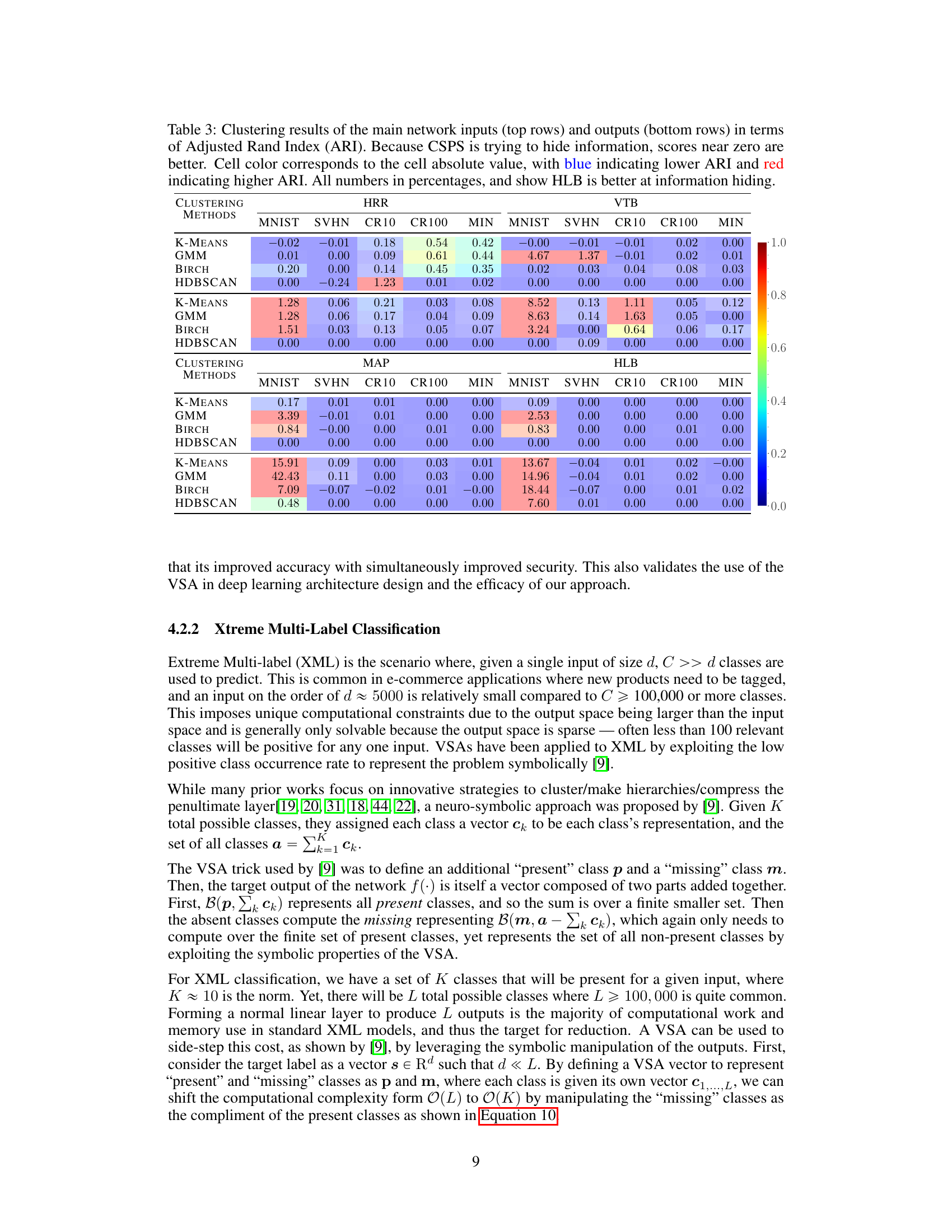
This table presents the results of clustering experiments conducted on the inputs and outputs of the Connectionist Symbolic Pseudo Secrets (CSPS) model. The goal of CSPS is to protect data privacy by obscuring the input and output. The Adjusted Rand Index (ARI) measures the similarity between the true cluster assignments and the clusters produced by the clustering algorithms. Lower ARI scores indicate better protection. The table compares the performance of four different vector symbolic architectures (VSAs): HRR, VTB, MAP, and HLB across five different datasets. The color-coding of the cells highlights the magnitude of the ARI, with darker blue indicating better privacy preservation.
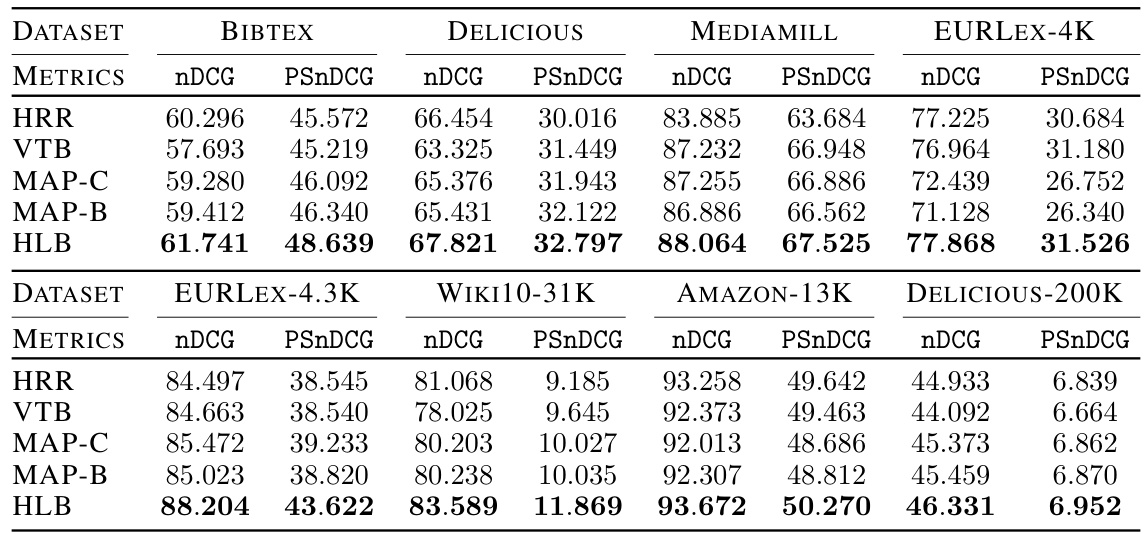
This table presents the results of extreme multi-label classification experiments using four different vector symbolic architectures (VSAs): HRR, VTB, MAP-C, MAP-B, and the proposed HLB. The performance is evaluated across eight datasets using two metrics: Normalized Discounted Cumulative Gain (nDCG) and Propensity-Scored nDCG (PSnDCG). The table highlights that the HLB consistently achieves the best performance across all datasets and metrics, establishing a new state-of-the-art (SOTA).
Full paper#