A Globally Optimal Portfolio for m-Sparse Sharpe Ratio Maximization

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it provides a globally optimal solution to the challenging problem of maximizing the Sharpe ratio with sparsity constraints. This addresses a critical need in portfolio optimization, where managing a large number of assets is impractical. The method’s efficiency and theoretical guarantees make it a valuable tool for researchers and practitioners.

Visual Insights

#

This figure displays the results of a simulation to validate the global optimality of the proposed proximal gradient algorithm (PGA). The left panel shows the normalized error of the iterative sequence (||v^(k)-v*||₂/||v*||₂) against the iteration number. The right panel shows the normalized error of the function value (|f(v^(k))-f(v*)|/|f(v*)|) against the iteration number. Both plots demonstrate the convergence of the PGA to the global optimum.

This table presents the Sharpe ratios achieved by eleven different portfolio optimization methods across six benchmark datasets. The methods include a naive 1/N strategy, several existing methods (SPOLC, SSPO, S1, S2, S3, SSMP, MAXER, IPSRM-D, PLCT), and the proposed mSSRM-PGA with three different sparsity levels (m=10, 15, 20). Two different time window sizes (T=60 and T=120) are considered. The table allows for a comparison of the Sharpe ratios generated by each method under different sparsity constraints and time window settings.

In-depth insights

#

m-Sparse SR Max

#

The heading ’m-Sparse SR Max’ likely refers to a method for maximizing the Sharpe Ratio (SR) while enforcing sparsity. The ’m’ denotes a constraint limiting the number of non-zero elements in the portfolio weight vector to at most ’m’ assets, thus creating a sparse portfolio. This sparsity is crucial for practical portfolio management, reducing transaction costs and simplifying portfolio administration. The ‘SR Max’ indicates that the goal is to find the portfolio that maximizes the Sharpe Ratio under this sparsity constraint. This is a challenging optimization problem because of the non-convex nature of the SR and the combinatorial nature of the sparsity constraint. The paper likely proposes a novel algorithm to tackle this problem, possibly by transforming the problem into a more tractable form (e.g., quadratic programming) and leveraging techniques that handle non-convexity and sparsity efficiently. A key contribution might be a guarantee of global or at least local optimality, which would be a significant advancement over existing heuristic methods. The algorithm’s performance would then be empirically evaluated using both synthetic and real-world financial datasets, showcasing its effectiveness in achieving high SR values with manageable portfolio size. Ultimately, the ’m-Sparse SR Max’ methodology would offer a practical and theoretically sound approach for portfolio optimization in situations where a limited number of assets are preferred.

PGA Algorithm

#

The Proximal Gradient Algorithm (PGA) is a crucial element in this research paper, designed to tackle the challenges of m-sparse Sharpe Ratio Maximization. This problem is inherently complex due to its non-convex nature, caused by the m-sparse constraint. The core idea of PGA is to iteratively approach the solution by combining a gradient descent step to minimize a quadratic approximation of the objective function, followed by a proximal operator. This proximal operator efficiently handles the non-smooth, non-convex m-sparse constraint, ensuring the solution remains feasible. The algorithm’s convergence is rigorously analyzed and proven to achieve a globally optimal solution under specified conditions, leveraging the Kurdyka-“Lojasiewicz (KL) property of the objective function. Convergence rates are also established, showcasing the algorithm’s efficiency. The practical significance of PGA lies in its ability to solve a real-world problem in finance; it allows for the construction of sparse portfolios which are both computationally efficient and lead to optimal risk-adjusted returns. Finally, the algorithm’s flexibility is highlighted, suggesting its adaptability to other optimization problems with semi-algebraic structures.

Global Optimality

#

The concept of ‘global optimality’ in the context of portfolio optimization is crucial. The paper focuses on achieving the best possible Sharpe ratio, not just a locally optimal solution. Finding a globally optimal m-sparse Sharpe ratio is challenging due to the non-convex nature of the problem and the m-sparse constraint. The authors cleverly transform the fractional optimization problem into an equivalent quadratic programming problem, making it more tractable. Their proposed Proximal Gradient Algorithm (PGA) leverages the Kurdyka-Łojasiewicz property to guarantee convergence to a globally optimal solution under specific conditions. This is a significant contribution as it provides a theoretically sound method for achieving true optimality. The algorithm’s efficiency and ability to handle realistic constraints are also highlighted. However, the global optimality guarantee hinges on certain conditions, such as the existence of a portfolio with a positive expected return. Further research could explore relaxation of these conditions and the algorithm’s robustness in more complex market scenarios.

Real-World Tests

#

A robust evaluation of any portfolio optimization strategy necessitates real-world testing. This involves applying the model to actual financial market data, assessing its performance against various benchmarks, and considering transaction costs and other realistic constraints. Real-world tests reveal the practical applicability and limitations of a model far more effectively than simulations. A key aspect is the choice of benchmark datasets; using diverse and representative data spanning different market conditions is crucial. The evaluation metrics should be comprehensive, including not only Sharpe ratios but also cumulative wealth, maximum drawdown, and turnover rates. A thorough analysis of results should discuss factors affecting performance, such as market regimes and model parameter choices. Furthermore, sensitivity analysis concerning transaction costs and the impact of various constraints (such as sparsity or short-selling restrictions) provides additional insights into the method’s robustness. Ultimately, the success of a real-world test lies in its ability to demonstrate the strategy’s effectiveness in generating consistent and risk-adjusted returns in a dynamic market environment.

Future Works

#

Future research could explore extending the m-sparse Sharpe Ratio Maximization (mSSRM) framework to handle non-differentiable numerators and denominators in fractional optimization problems. This would significantly broaden the applicability of the method to a wider range of portfolio optimization and machine learning challenges. Investigating alternative optimization algorithms beyond the Proximal Gradient Algorithm (PGA), such as stochastic gradient methods or second-order methods, could potentially improve the efficiency and scalability of mSSRM, especially for high-dimensional datasets. A rigorous analysis of the algorithm’s robustness to noise and model misspecification is crucial for practical applications. Further research should explore the impact of various regularization techniques and their influence on the sparsity and performance of the resulting portfolio. Finally, empirical studies comparing the performance of mSSRM against other state-of-the-art sparse portfolio optimization methods across different market conditions and asset classes would provide valuable insights and strengthen the method’s practical relevance.

More visual insights

#

More on tables

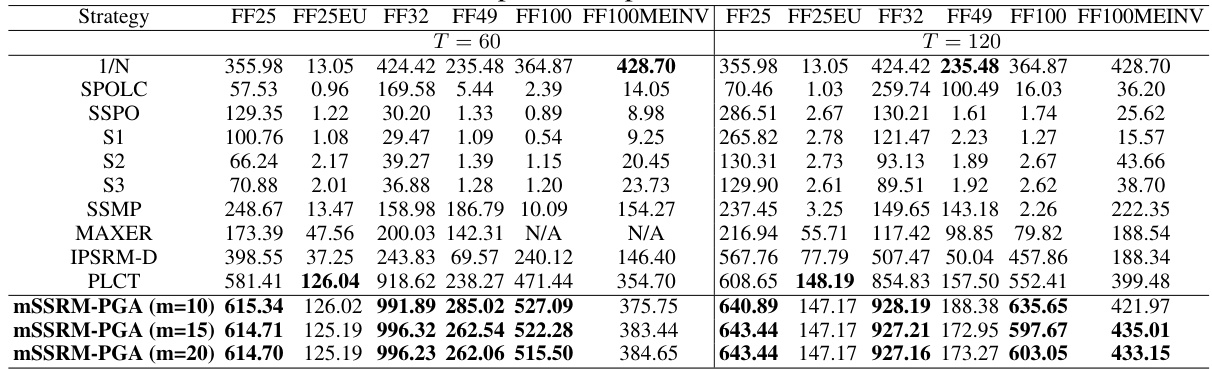
This table presents the final cumulative wealth achieved by eleven different portfolio optimization methods across six benchmark datasets. The methods include a naive 1/N strategy and several state-of-the-art techniques, compared against the proposed mSSRM-PGA method with varying sparsity levels (m=10, 15, 20). The results are shown for two different time window sizes (T=60 and T=120) to simulate different portfolio rebalancing frequencies. The table allows for comparison of portfolio performance based on cumulative wealth, providing insights into the overall profitability of each method.

This table presents the sparsity of portfolios generated by the mSSRM-PGA algorithm for different sparsity levels (m = 10, 15, 20) and time window sizes (T = 60, 120). The mean and standard deviation (STD) of the cardinality of the support set of ŵ(t) (|supp(ŵ(t))|) are shown for six different real-world benchmark datasets. This shows how the algorithm’s generated portfolios maintain sparsity even with varying parameters and datasets.

This table presents the results of simulation experiments conducted to validate the global optimality of the proposed Proximal Gradient Algorithm (PGA). Ten experiments were run, each with 500 iterations of PGA using three different initializations (0N, 1N/N, and 1n). The table displays the normalized errors of the iterative sequence (||v(k) - v*||2/||v*||2) and the normalized errors of the function value (|f(v(k)) - f(v*)|/|f(v*)|) at the 500th iteration for each of the ten experiments. These normalized errors measure how close the algorithm’s solution at the 500th iteration is to the true globally optimal solution, providing evidence for the effectiveness of the PGA in achieving global optimality.

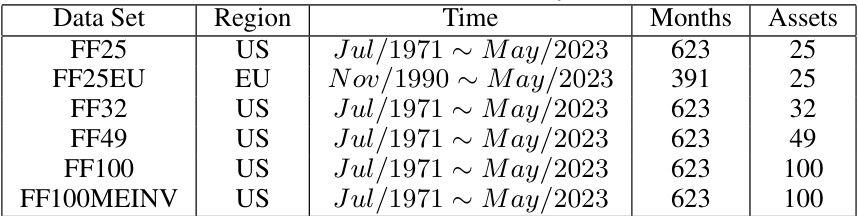
This table presents information about six real-world monthly benchmark datasets used in the paper’s experiments. For each dataset, it lists the region (US or EU), the time period covered, the number of months in the time period, and the number of assets included.

This table presents a comparison of the performance of SDP Relaxation and the proposed mSSRM-PGA algorithm on six benchmark datasets. The results show the final cumulative wealth and Sharpe ratios achieved by each method for different sparsity levels (m=10,15,20) with a time window of 60 periods (T=60). This helps assess the effectiveness of mSSRM-PGA compared to an alternative approach.

This table shows the average running time (in seconds) for each of the 11 portfolio optimization methods across six benchmark datasets. The running time is measured for a single period of optimization. The datasets used are FF25, FF25EU, FRENCH32, FF49, FF100, and FF100MEINV. The methods compared include SPOLC, SSPO, S1, S2, S3, SSMP, MAXER, IPSRM-D, PLCT, SDP Relaxation, and the proposed mSSRM-PGA. The table provides insights into the computational efficiency of each method.

Full paper

#