↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Training large language models (LLMs) is computationally expensive, especially as model sizes grow. Existing memory-efficient methods often compromise performance or lack theoretical guarantees. This paper addresses these issues by introducing Online Subspace Descent (OSD), a new optimization technique that leverages low-rank structures for efficient training. Existing methods, like GaLore and Sketchy, rely on expensive SVD for projection, hindering scalability. Furthermore, the convergence of these methods depends on specific update rules which limits applicability.
OSD addresses these problems by using online PCA instead of SVD to dynamically update the subspace, significantly reducing computational overhead. Importantly, the paper provides a convergence guarantee for OSD for a large class of optimizers. This theoretical guarantee expands the applicability beyond specific algorithms. Empirical results show that OSD achieves lower perplexity and better downstream task performance than current state-of-the-art low-rank training methods across different model sizes, closing the gap with full-rank baselines.
Key Takeaways#
Why does it matter?#
This paper is important because it offers a novel solution to the memory limitations of training large language models (LLMs). By introducing Online Subspace Descent, it provides a more efficient training method that closes the performance gap with full-rank baselines. This is especially crucial given the growing size and complexity of LLMs, pushing the boundaries of current computational resources. The convergence guarantee provided is a significant theoretical contribution, advancing the understanding of subspace descent optimizers. Furthermore, the method’s flexibility and ease of implementation make it practical for broader adoption.
Visual Insights#

This figure displays the validation perplexity achieved by three different methods (AdamW (8bit), Ours (AdamW 8bit), and GaLore (AdamW 8bit)) during the training of a 1B parameter LLaMA model with a sequence length of 256 and a rank of 512. The x-axis represents the training steps (up to 10K steps), and the y-axis represents the validation perplexity. The figure demonstrates how the perplexity changes over the training process for each method. This allows for a comparison of the different approaches’ effectiveness in reducing perplexity during model training.
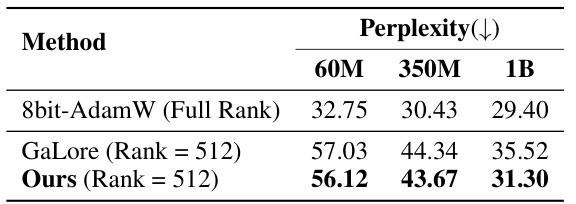
This table presents the perplexity results for pretraining a 1B parameter LLaMA model using different methods. The training involved a sequence length of 256 and ran for 10,000 steps. Perplexity is reported as the average of the last 10 steps of training. The baseline optimizer used for comparison is 8-bit AdamW.
In-depth insights#
LLM Memory Limits#
Large language models (LLMs) are computationally expensive, and their memory requirements are a significant bottleneck. The memory needed to store the model’s parameters and activations grows rapidly with model size, leading to limitations on training and inference. Efficient training techniques like low-rank adaptation, quantization, and gradient checkpointing are crucial to mitigate these issues. However, these methods often involve trade-offs, reducing model accuracy or increasing training time. Hardware advancements such as specialized memory architectures and improved parallel processing are also vital to push LLM memory boundaries further. Research into novel model architectures that require less memory, while maintaining or even improving performance, is a critical area of ongoing exploration in the field.
Online Subspace Descent#
Online Subspace Descent presents a novel approach to memory-efficient training of large language models (LLMs). It addresses the limitations of existing methods that rely on periodic Singular Value Decomposition (SVD) for subspace projection by employing online Principal Component Analysis (PCA). This dynamic update strategy offers significant advantages: it avoids the computational cost of SVD, making training more efficient, and allows for adaptive subspace selection, potentially leading to faster convergence. The method’s flexibility is highlighted by its compatibility with various optimizers, further enhancing its practicality. Theoretical analysis provides a convergence guarantee for arbitrary update rules of the projection matrix, underscoring the robustness of the approach. The experimental results, showing lower perplexity and improved downstream task performance compared to state-of-the-art baselines, validate the effectiveness of Online Subspace Descent as a memory-efficient LLM training technique. The trade-off between rank and performance is also explored, providing valuable guidance for practical applications.
Hamiltonian Convergence#
The concept of “Hamiltonian Convergence” in the context of optimization algorithms for large language models (LLMs) offers a powerful framework for analyzing the dynamic behavior of memory-efficient training methods. It leverages the Hamiltonian formalism from physics, representing the optimization process as a dynamical system with a Hamiltonian function. Convergence is then analyzed by examining the behavior of this Hamiltonian function over time. This approach has several advantages. First, it provides a unified way to understand various optimizers, establishing connections between seemingly disparate methods. Second, it offers a pathway to proving convergence guarantees, even for non-convex objective functions, a significant challenge in LLM training. The focus on the Hamiltonian allows for rigorous mathematical analysis, potentially leading to the development of more robust and efficient optimization strategies. By carefully studying the evolution of the Hamiltonian, researchers can gain deeper insights into the learning dynamics, identifying potential bottlenecks and suggesting improvements. The core idea is to design optimizers that exhibit a monotonic decrease in the Hamiltonian, ultimately ensuring convergence toward optimal model parameters. This approach is especially valuable in the context of subspace descent methods, where the projection of the gradient onto a lower-dimensional subspace plays a crucial role. The Hamiltonian framework facilitates a more precise understanding of how these projection techniques affect the convergence behavior, paving the way for improved memory-efficient LLM training.
Online PCA Updates#
Online Principal Component Analysis (PCA) offers a compelling approach to dynamically adapt low-rank approximations in large-scale machine learning. Its key advantage lies in efficiently updating the projection matrix without the computational burden of full singular value decomposition (SVD) at each iteration. This is crucial for memory-efficient training of large language models (LLMs), as SVD becomes prohibitively expensive for high-dimensional parameter spaces. By using online PCA, the method can incrementally incorporate new gradient information, leading to a more responsive and adaptive low-rank approximation of the gradient. The continuous update of the projection matrix allows the optimization process to effectively navigate the parameter space, avoiding the limitations of periodic SVD updates that might lag behind the evolving gradient dynamics. This approach enhances the algorithm’s ability to capture the most significant directions within the data, effectively mitigating the memory constraints without significant performance loss. The theoretical analysis is critical to understanding the convergence properties, especially for non-convex functions which are common in training deep neural networks. The balance between computational efficiency and convergence guarantees makes online PCA updates a powerful tool in tackling the challenges of scaling up machine learning algorithms to ever larger model sizes.
Future Research#
The ‘Future Research’ section of this paper offers exciting avenues for extending the work on memory-efficient LLMs. Further investigation into alternative projection matrix update methods is crucial, exploring techniques beyond online PCA to potentially accelerate convergence and enhance performance. The impact of weight decay on the dynamic subspace descent algorithm also requires thorough analysis, as it may significantly influence the optimization process. Combining low-rank gradients with dynamic low-rank weights, such as in Mixture of Experts models, could dramatically increase training efficiency and model capacity. Finally, the authors rightly point out the need to explore the applicability of this framework beyond language modeling, potentially impacting diverse areas like computer vision and other deep learning tasks. This broad range of potential future work highlights the significant contribution of the paper and its potential for substantial advancements in the field.
More visual insights#
More on figures
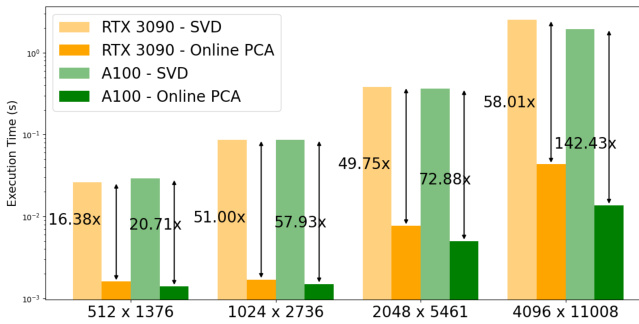
This figure compares the execution time of singular value decomposition (SVD) and online principal component analysis (PCA) for updating the projection matrix in the Online Subspace Descent algorithm. It shows that online PCA is significantly faster than SVD, especially for larger matrices, which is crucial for efficient training of large language models. The speed advantage of online PCA allows for parallel updates, minimizing training overhead.
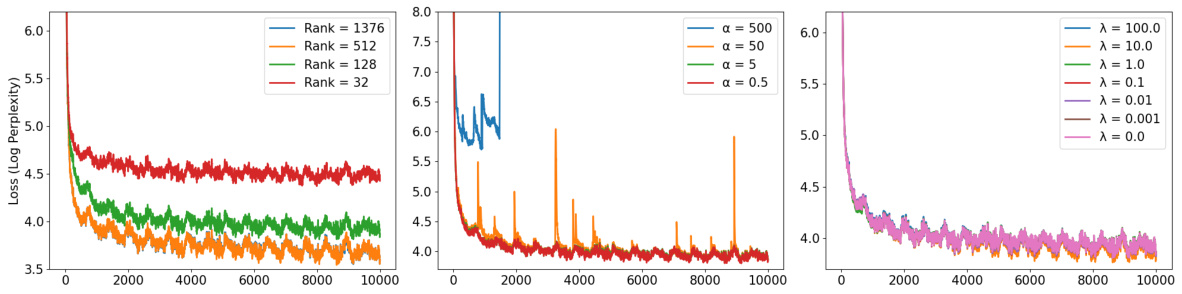
This figure shows the loss curves for three hyperparameter sweeps during the training of a 60M parameter LLaMA model. The leftmost plot shows how loss changes with different ranks of the projection matrix. The middle plot demonstrates the impact of the α parameter (which controls the update speed of the projection matrix) on the loss. Finally, the rightmost plot illustrates how loss varies based on the λ parameter, which handles regularization in the PCA update of the projection matrix.
More on tables

This table shows the perplexity results for different combinations of optimizers used for updating the model weights (Wt) and the projection matrix (Pt) in the Online Subspace Descent method. The experiment is conducted on the LLaMA 60M model with a sequence length of 1024 using the C4 dataset. The table compares the performance of Online Subspace Descent against GaLore, showing that different combinations of optimizers can lead to varying performance levels. The abbreviations Adaf. and Adam refer to Adafactor and 8-bit AdamW respectively.

This table presents the results of pretraining a 7B parameter LLaMA model on the C4 dataset for 10,000 steps using both the Galore and the proposed Online Subspace Descent methods. It compares the final perplexity achieved (lower is better, indicating better model performance) and the wall-clock time (in hours) required for training. The table highlights that Online Subspace Descent achieves a lower perplexity and a faster training time than Galore.

This table presents the results of downstream task evaluations on a 7B parameter Language Model. The model was evaluated on six tasks from the GLUE benchmark: MRPC, RTE, SST-2, MNLI, QNLI, and QQP. The table compares the performance of the proposed ‘Ours’ method against the baseline Galore method, reporting the average score across all six tasks. The scores likely represent accuracy or F1-scores, common metrics for these tasks, showcasing the relative performance improvement achieved by the proposed method on various downstream applications of the language model.
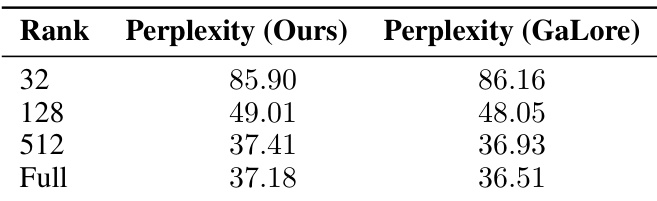
This table presents the results of an ablation study on the rank of the Online Subspace Descent method. It shows the perplexity achieved by the method at different ranks (32, 128, 512) and compares it to the perplexity obtained with the full rank model and GaLore method. The results demonstrate that higher ranks lead to lower perplexity, closing the gap to the full-rank baseline, but the improvement diminishes with increasing rank.

This table presents the perplexity results of the LLaMA 60M model trained on the C4 dataset with a sequence length of 1024. Different combinations of optimizers are used for updating the model weights (Wt) and the projection matrix (Pt). The table compares the performance of different optimizer combinations (e.g., Lion + Lion, Adafactor + Adafactor, AdamW8bit + AdamW8bit) and their Galore counterparts. Adaf. is an abbreviation for Adafactor, and Adam refers to 8bit-AdamW.
Full paper#



















