↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Simple bilevel optimization problems involve minimizing an upper-level function while satisfying the optimal solution of a lower-level function. Existing methods struggle to find precise solutions due to the inherent complexity of these problems. This often results in settling for approximate solutions, but even these are difficult to obtain using standard first-order methods.
This paper addresses this by proposing a novel approach, FC-BiO (Functionally Constrained Bilevel Optimizer). FC-BiO cleverly transforms the bilevel problem into a functionally constrained one. By doing so, the authors develop methods capable of finding near-optimal solutions. This is a significant contribution because it provides both theoretical guarantees and practical algorithms that are demonstrably better than previously available methods. The algorithm’s effectiveness is validated through numerical experiments demonstrating its superior performance on benchmark problems.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on bilevel optimization problems. It highlights the fundamental difficulties in finding exact solutions and proposes novel near-optimal algorithms that address these challenges. This work opens avenues for developing more efficient methods in various machine learning and AI applications, advancing the state-of-the-art in simple bilevel optimization.
Visual Insights#
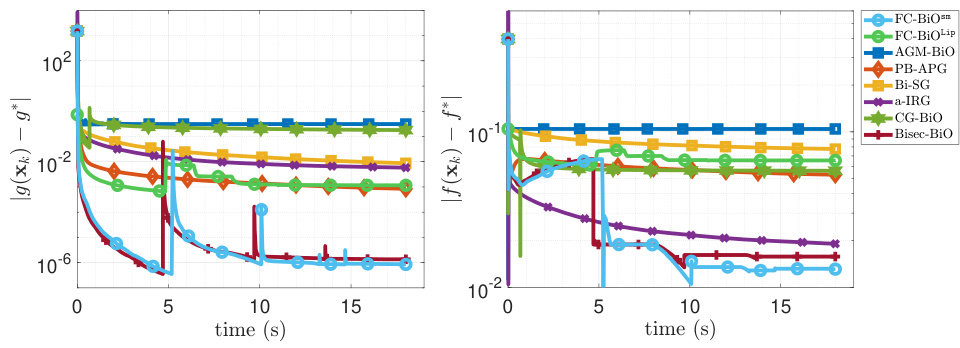
This figure compares the performance of the proposed algorithm (FC-BiO) with several other algorithms (FC-BiOLip, AGM-BIO, PB-APG, Bi-SG, a-IRG, CG-BIO, and Bisec-BiO) on solving Problem (11), a simple bilevel problem with smooth objectives. The x-axis represents the computation time, and the y-axis shows the difference between the current objective values and the optimal value for both the upper-level function (f(x) - f*) and the lower-level function (g(x) - g*). The plot demonstrates how quickly each algorithm converges towards the optimal solution.
Full paper#



















