↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world machine learning tasks suffer from long-tailed data distributions: a skewed distribution with many classes having only a few samples and a few classes having many samples. Semi-supervised learning (SSL) which uses both labeled and unlabeled data can improve the performance in this case, but most SSL methods assume a balanced label distribution which is not realistic. Long-tailed semi-supervised learning (LTSSL) is therefore a challenging problem.
This paper introduces a new method called Continuous Contrastive Learning (CCL). CCL uses a probabilistic framework that unifies several recent approaches to long-tailed learning and extends it to the semi-supervised setting. CCL leverages a class-balanced contrastive loss, using both labeled and unlabeled data. Key to CCL’s success is the use of smoothed pseudo-labels generated from the model to help address the challenges of learning with imbalanced unlabeled data. The experimental results demonstrated that CCL consistently outperforms state-of-the-art methods across several datasets.
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles the critical problem of long-tailed semi-supervised learning, a common challenge in real-world applications where labeled data is scarce and imbalanced. The proposed CCL method significantly outperforms existing approaches, offering a more robust solution for various real-world scenarios and opening new avenues for research in improving representation learning and handling diverse label distributions.
Visual Insights#
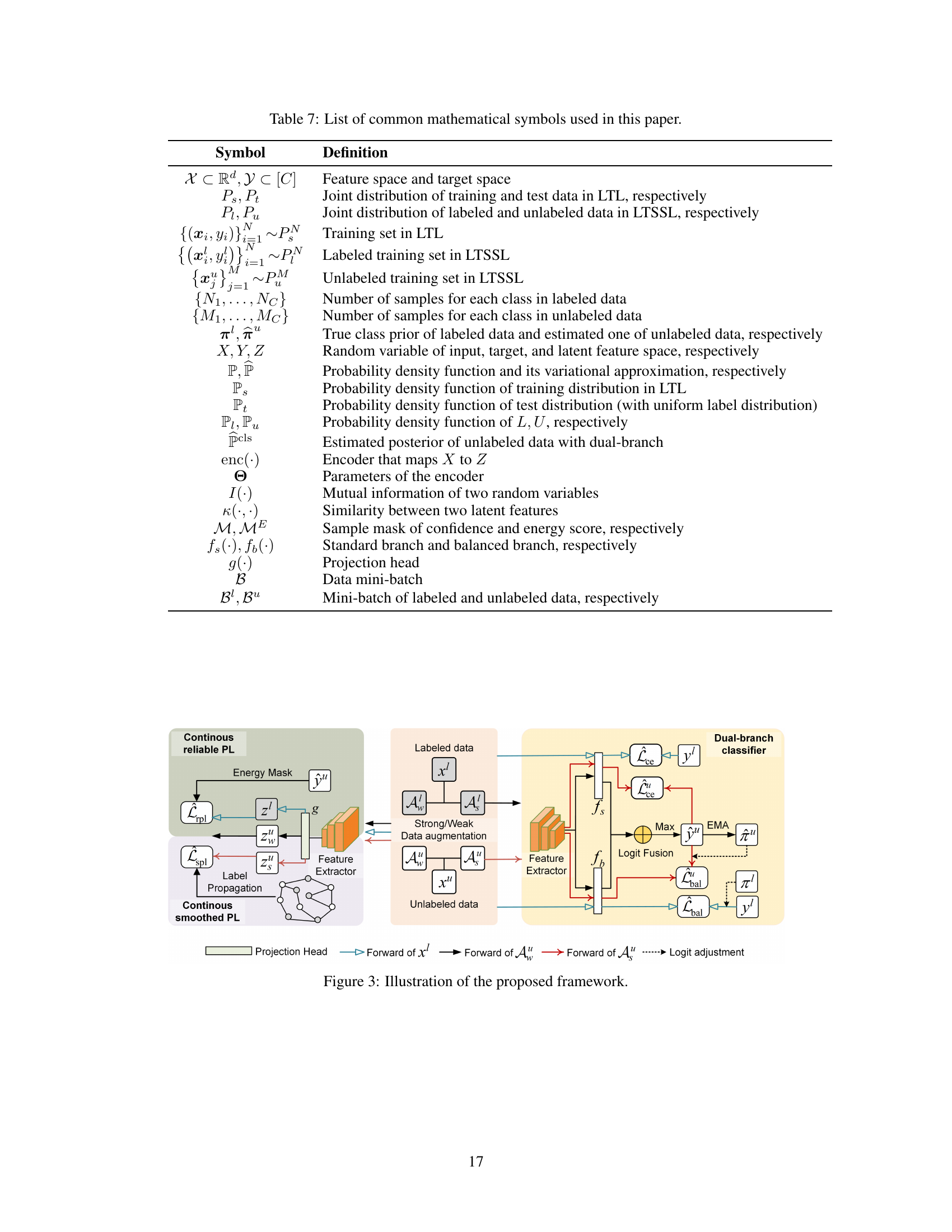
This figure illustrates the overall framework of the proposed CCL method. It consists of two main parts: the classification part and the contrastive learning part. The classification part utilizes logit rectification of the classifier by class prior estimated with a dual-branch. For the contrastive learning part, the energy score is used to select reliable unlabeled data, which are merged with labeled data for continuous contrastive loss to ensure calibration. Besides, information of labeled data and unlabeled data are used in a decoupled manner while maintaining the constraints of aligning features in the contrastive learning space, thereby forming a smoothed contrastive loss.
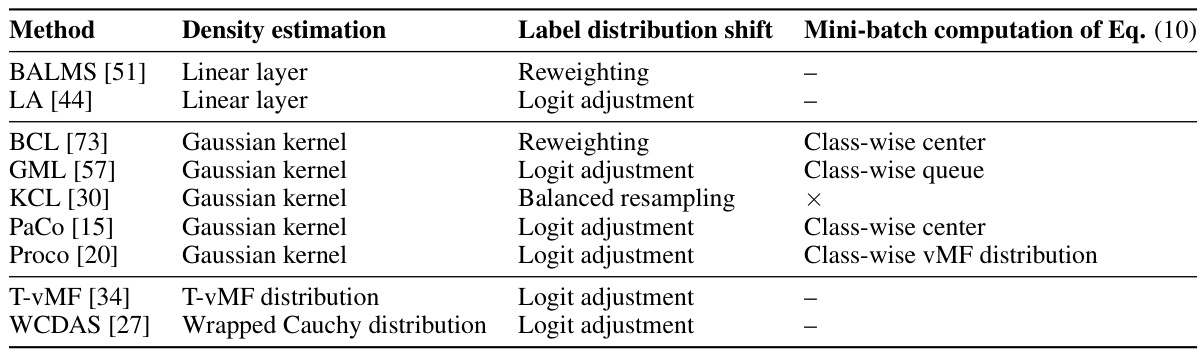
This table categorizes several popular long-tail learning methods based on three key aspects: the approach used for density estimation (linear layer, Gaussian kernel, etc.), how they address label distribution shift (reweighting, logit adjustment, etc.), and their mini-batch computation strategy for a specific equation in the paper. The table shows how these methods relate to the proposed framework in the paper.
In-depth insights#
LTSSL Framework#
The proposed LTSSL framework offers a novel probabilistic approach to address the challenges of long-tailed semi-supervised learning. It unifies several existing long-tail learning methods, providing a theoretical foundation for understanding their connections and limitations. The framework leverages Gaussian kernel density estimation to derive a class-balanced contrastive loss, effectively handling class imbalance in both labeled and unlabeled data. A key innovation is the introduction of continuous contrastive learning (CCL), which utilizes reliable and smoothed pseudo-labels to improve representation learning and mitigate confirmation bias, a common problem in semi-supervised settings. Progressive estimation of the underlying label distribution further enhances the robustness of the model by adapting to diverse unlabeled data distributions. The framework demonstrates improved performance across multiple datasets, highlighting the value of its probabilistic approach and continuous contrastive learning strategy in achieving state-of-the-art results in LTSSL.
CCL Algorithm#
The Continuous Contrastive Learning (CCL) algorithm, as described in the research paper, presents a novel approach to long-tailed semi-supervised learning. CCL addresses the issue of biased pseudo-label generation, a common problem in semi-supervised settings with imbalanced data, by progressively estimating the underlying label distribution and aligning model predictions with this distribution. A key innovation is the use of continuous pseudo-labels, derived from model predictions and propagated labels, to improve the reliability of the unlabeled data. Unlike prior methods, CCL explicitly focuses on representation learning, leveraging an information-theoretic framework to learn effective representations and unify various recent long-tail learning proposals. The algorithm incorporates a class-balanced contrastive loss, enhanced by Gaussian kernel density estimation, and further refined with a complementary contrastive loss to improve representation quality. The dual-branch training scheme allows for both balanced and standard classification training, mitigating the harmful effects of strictly balanced training on representation learning. CCL’s comprehensive experimental evaluation demonstrates consistent outperformance over state-of-the-art methods across multiple datasets, showcasing its robustness and effectiveness in handling real-world scenarios with varying label distributions.
Empirical Results#
An Empirical Results section should present a thorough evaluation of the proposed method, comparing its performance against relevant baselines and state-of-the-art techniques. The results should be presented clearly and concisely, using tables and figures to visualize key findings. Quantitative metrics such as accuracy, precision, recall, and F1-score should be reported, along with statistical significance tests to ensure robustness. The experiments should be designed to address specific research questions and evaluate different aspects of the model’s performance under varied conditions. A detailed description of the experimental setup, including datasets, hyperparameters, and training procedures, must be provided to ensure reproducibility. Discussion of the results should highlight both strengths and limitations, offering interpretations of the findings, explaining unexpected outcomes, and drawing conclusions that answer the research questions. The Empirical Results section should be well-structured, logical, and insightful, providing compelling evidence to support the paper’s claims.
Ablation Study#
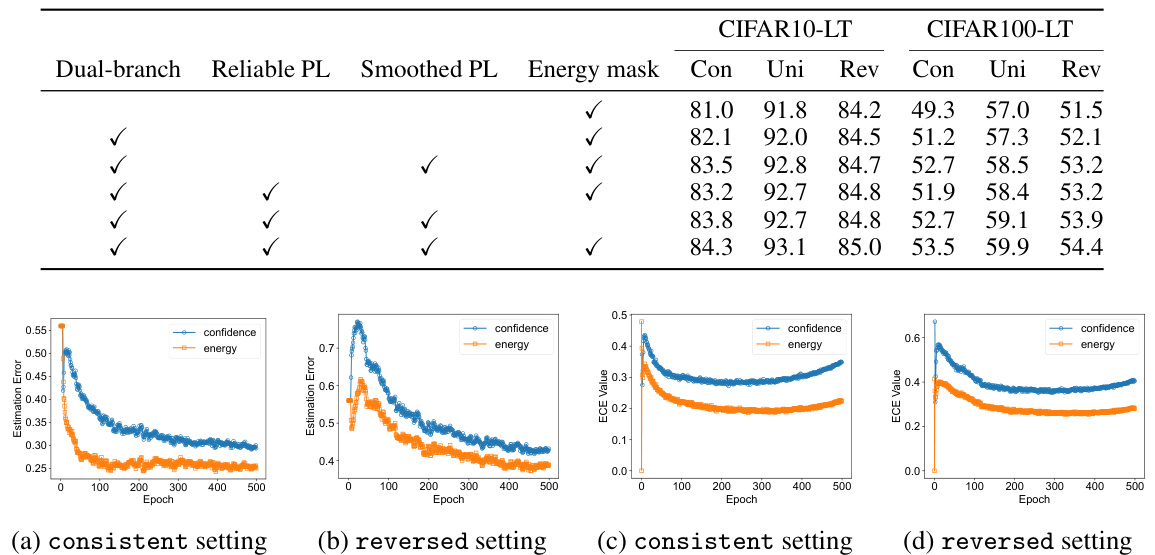
An ablation study systematically removes components of a model or system to determine their individual contributions. In a machine learning context, this could involve removing layers from a neural network, disabling specific regularization techniques, or altering aspects of the training process. The goal is to isolate the impact of each element, providing valuable insights into model design and performance. A well-conducted ablation study helps answer crucial questions such as: which parts are essential for achieving high accuracy, what are the trade-offs between different components, and where the model is most sensitive. Results are typically presented in a tabular format, showing performance metrics with and without each removed component. Careful interpretation is needed, as interactions between components can complicate the analysis. A robust ablation study provides strong evidence for the importance of specific design choices, contributing significantly to the understanding of the model’s workings and potentially guiding future improvements.
Future Works#
Future work could explore several promising avenues. Extending CCL to other semi-supervised learning paradigms beyond FixMatch, such as those employing consistency regularization or pseudo-labeling methods, would broaden its applicability and robustness. Investigating the effect of different kernel functions within the proposed probabilistic framework is also warranted, as different kernels might offer different performance characteristics for various datasets. A theoretical analysis of the framework’s convergence properties would provide a deeper understanding of its behavior. This could involve proving theoretical bounds on the generalization error or examining the impact of hyperparameters on convergence speed and stability. Analyzing the scalability of CCL to extremely large-scale datasets like the full ImageNet is crucial. This might involve exploring efficient training strategies or distributed training approaches. Finally, a thorough investigation of the model’s sensitivity to noise and outliers in both labeled and unlabeled data should be conducted, aiming to develop strategies to improve resilience and accuracy under less-than-ideal data conditions.
More visual insights#
More on figures

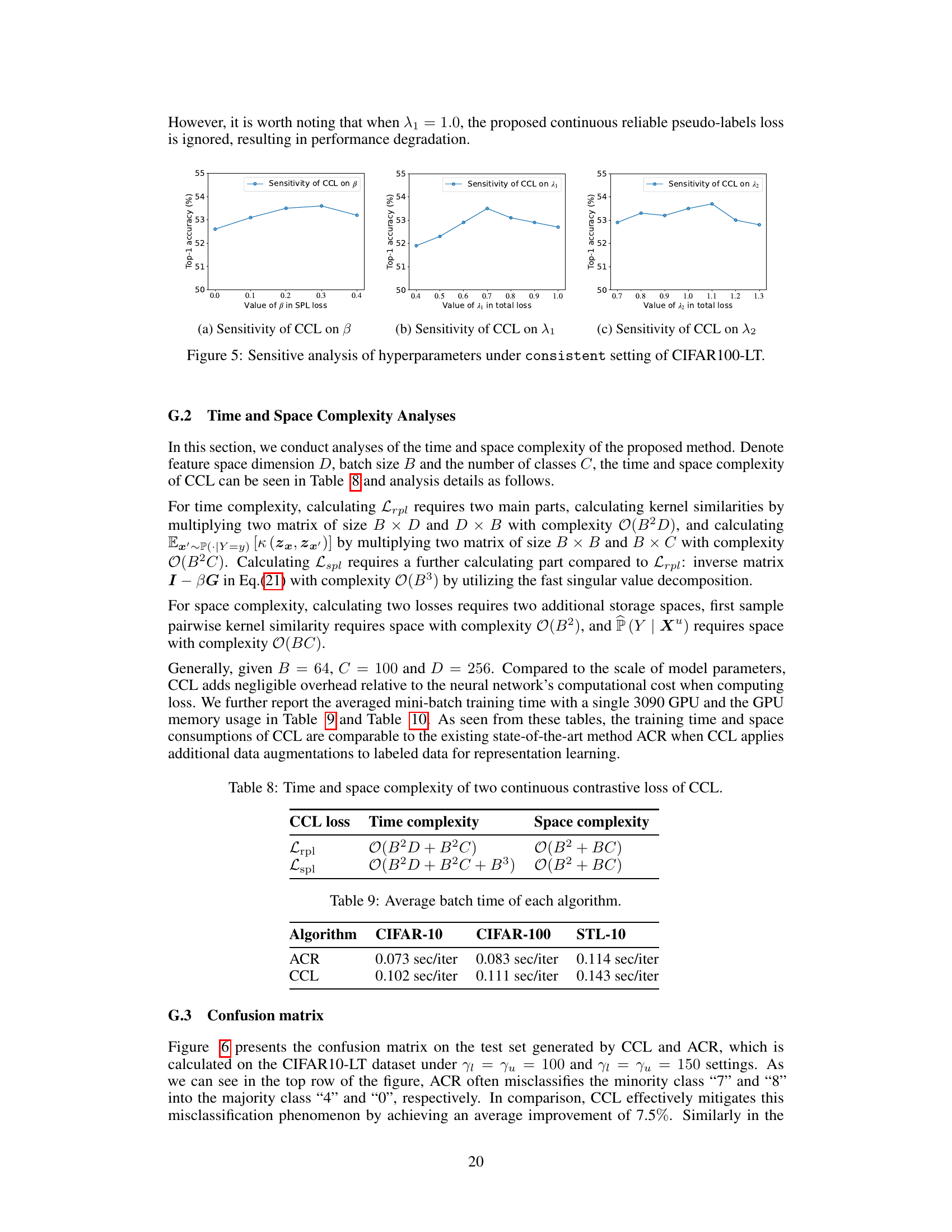
This figure presents a sensitivity analysis of three key hyperparameters in the CCL model: beta (β), lambda1 (λ₁), and lambda2 (λ₂). Each subplot shows how the top-1 accuracy changes as the value of a specific hyperparameter varies while holding others constant. The x-axes represent the range of values tested for each hyperparameter, and the y-axis displays the corresponding top-1 accuracy. The consistent setting of the CIFAR100-LT dataset was used for this analysis. The results illustrate the robustness of CCL to changes in these hyperparameters within a reasonable range.

The figure illustrates the overall framework of the proposed CCL method. It shows the dual-branch classifier, logit fusion, and the components for continuous reliable and smoothed pseudo-labels, including data augmentation, energy mask, and label propagation. The different branches, labeled and unlabeled data processing, and the merging of different loss functions (classification loss, continuous reliable pseudo-label loss, and continuous smoothed pseudo-label loss) are clearly shown. The figure provides a visual representation of how the different parts of the CCL algorithm interact to learn representations from both labeled and unlabeled data, especially in the long-tailed setting.
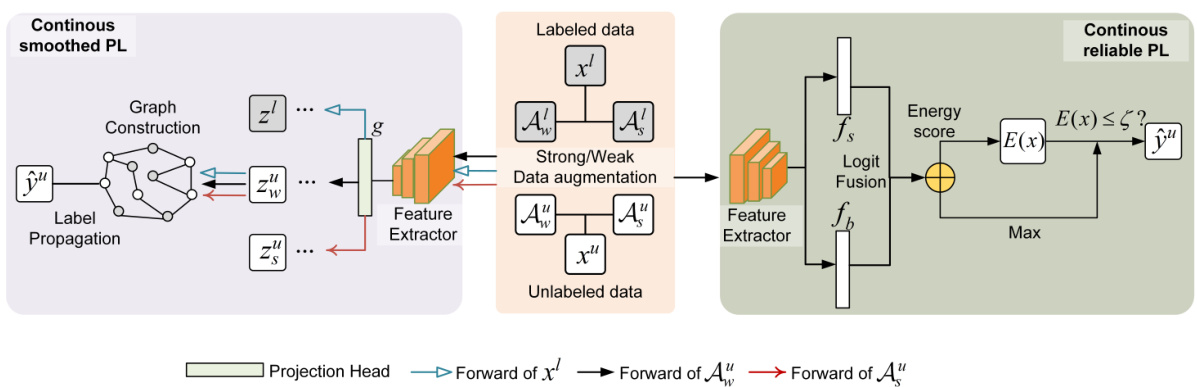
This figure illustrates the overall framework of the proposed Continuous Contrastive Learning (CCL) method. It shows the data flow, highlighting the key components: dual-branch classifiers (fs and fb), feature extractors, projection head (g), data augmentation techniques (Aw and As), energy score-based filtering for reliable pseudo-labels, and label propagation for smoothed pseudo-labels. The figure visualizes how labeled and unlabeled data are processed, and how the balanced classification loss, reliable continuous contrastive loss, and smoothed continuous contrastive loss are integrated to optimize the model’s performance.
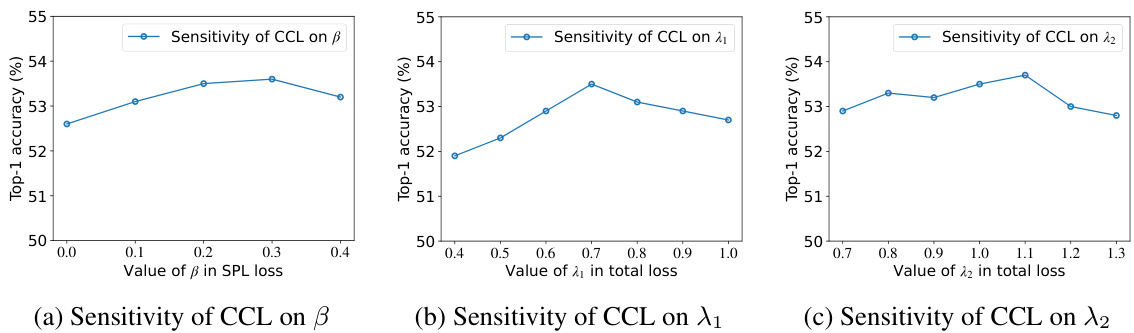
This figure shows the sensitivity analysis of three hyperparameters in the CCL model on the CIFAR100-LT dataset under a consistent setting. Three sub-figures display the effect of varying beta (β) in the smoothed pseudo-labels loss, lambda1 (λ₁) in the total loss, and lambda2 (λ₂) in the total loss, respectively, on the top-1 accuracy. The plots illustrate the robustness of the model’s performance to changes in these hyperparameters within a certain range, demonstrating the stability and effectiveness of the proposed approach.
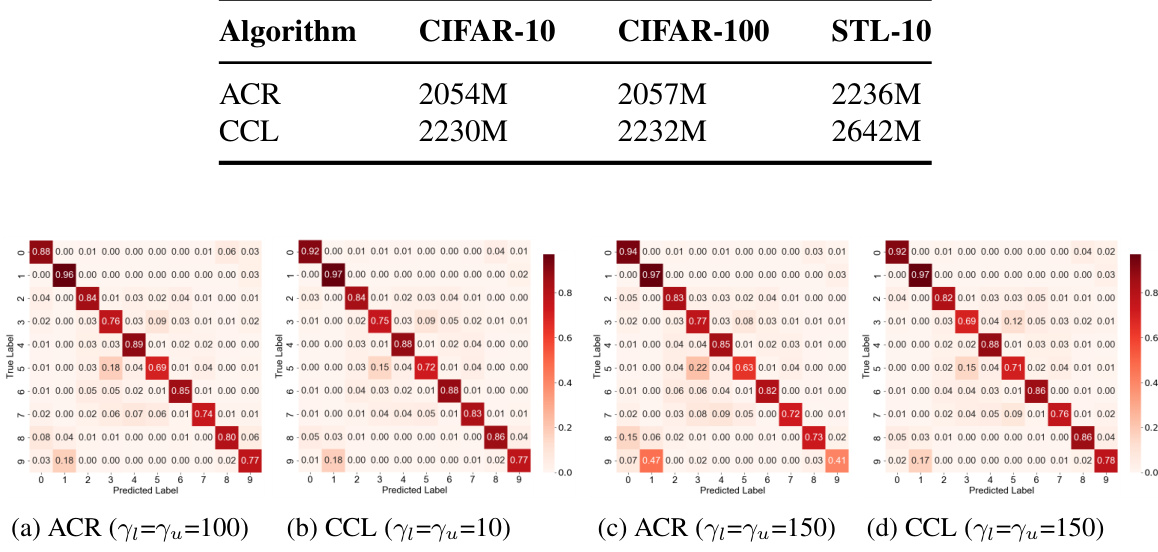
This figure displays confusion matrices for both ACR and CCL methods, applied to the CIFAR10-LT dataset under different settings of imbalance ratio (γl = γu = 100 and γl = γu = 150). The matrices visually represent the model’s performance in correctly classifying images, showing the counts of true positive and false positive classifications for each class. By comparing the matrices, the improvement of CCL over ACR in accurately classifying images (especially those in minority classes) is evident.
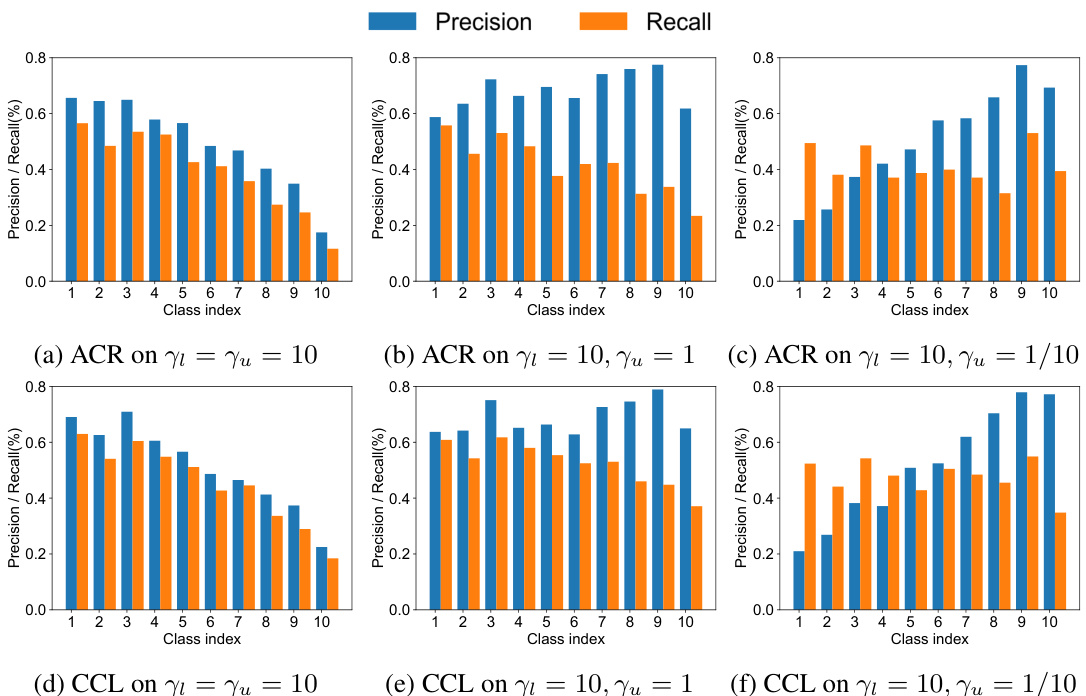
This figure shows the precision and recall of pseudo-labels generated by ACR and CCL on the CIFAR100-LT dataset under different settings of labeled and unlabeled data distributions. The consistent setting implies that both labeled and unlabeled data follow the same long-tailed distribution. The uniform setting means the unlabeled data distribution is uniform, whereas the reversed setting means the unlabeled data has an inverted long-tailed distribution. The figure visually compares the performance of ACR and CCL in terms of precision and recall across different class indexes under various data distribution settings.

This figure compares the precision and recall of pseudo-labels generated by ACR and CCL on the CIFAR100-LT dataset under different label distribution scenarios. It presents six subplots, two for each scenario (consistent, uniform, reversed). Each subplot shows the precision and recall for each of the ten classes (grouped from the original 100), allowing for a direct comparison of the two methods across various conditions of label distribution. This visualization aids in understanding the performance differences between the two methods, and how their ability to generate reliable pseudo-labels varies under different levels of class imbalance and label distribution shifts.

This figure uses t-SNE to visualize the learned representations from ACR and CCL on the CIFAR-10-LT dataset. The visualizations are shown for two different imbalance ratios (γι = γυ = 100 and γι = γυ = 150). Each point represents a data point from the test set, and the color indicates its true class label. The red circles highlight areas where the classification boundaries are less well-defined in ACR, indicating that CCL produces more distinct clusters and better separation of classes, particularly for those with imbalanced data representation.
More on tables
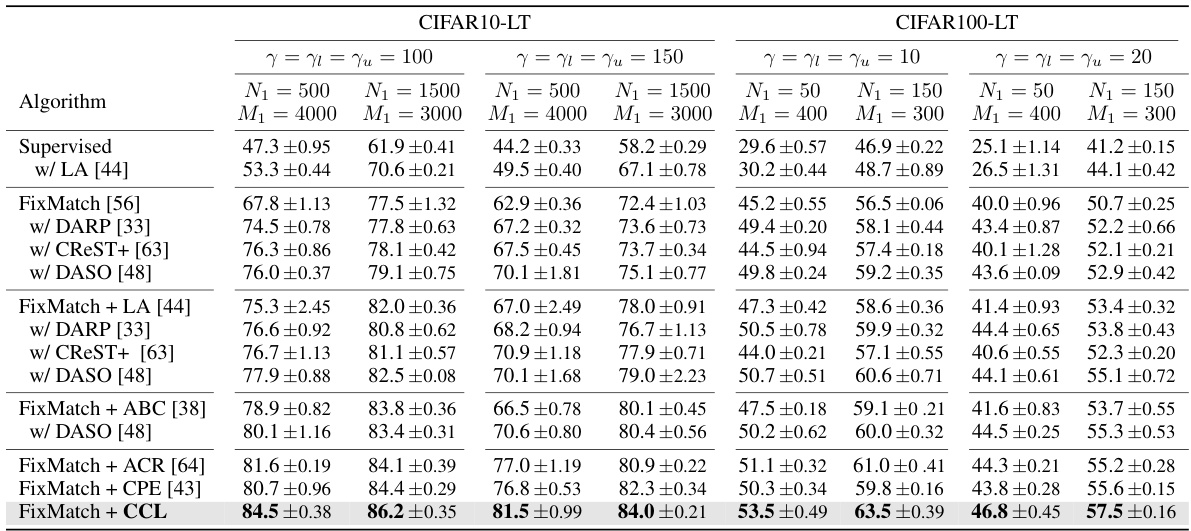
This table presents the test accuracy results for different semi-supervised long-tailed recognition methods on CIFAR10-LT and CIFAR100-LT datasets. The experiments were conducted under consistent settings, meaning that the imbalance ratio of labeled and unlabeled data is the same. The table shows the performance of several baselines (FixMatch, FixMatch with various improvements) and the proposed CCL method under various hyperparameter settings. The best-performing method for each configuration is highlighted in bold.

This table presents the test accuracy results of several algorithms on CIFAR10-LT and STL10-LT datasets under inconsistent settings, where the imbalance ratio of labeled data (γι) is different from that of unlabeled data (γu). The results show the performance under different γι and γu values, with the best results highlighted in bold.

This table shows the test accuracy results of different algorithms under various inconsistent settings (where the imbalance ratio of labeled data is not equal to that of unlabeled data). It presents results for two datasets (CIFAR10-LT and STL10-LT) with different labeled data imbalance ratios (γι) and various unlabeled data imbalance ratios (Yu), highlighting the robustness of the algorithms in handling real-world scenarios with data distribution shifts. The best-performing algorithm for each setting is indicated in bold.

This table presents the test accuracy results on the ImageNet-127 dataset for various long-tailed semi-supervised learning methods. The results are categorized by image size (32x32 and 64x64 pixels) and the method used. The best-performing method for each category is highlighted in bold, showcasing the relative performance of different approaches in long-tailed recognition tasks.
This table provides a comparison of several popular long-tail learning methods. It shows how these methods can be viewed through the lens of the proposed probabilistic framework, highlighting their approaches to density estimation (how they approximate the distribution of data), how they handle label distribution shift (differences between the training and test data distributions), and the mini-batch computation method used. The framework helps to unify seemingly different approaches by showing their commonalities.

This table provides a comparison of various long-tail learning methods, categorized by their approach to density estimation, handling of label distribution shifts, and mini-batch computation. It highlights how these methods relate to the proposed probabilistic framework introduced in the paper.

This table shows the average time taken to process one batch of data for different algorithms (ACR and CCL) across three different datasets (CIFAR-10, CIFAR-100, and STL-10). The results show the computational efficiency of each algorithm for a given batch size.
Full paper#