↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current methods for quantifying uncertainty in deep learning, like Deep Ensembles, often provide unreliable estimates, especially when dealing with unexpected data. This is a significant problem for applications requiring high reliability, such as autonomous vehicles or medical diagnosis. There’s also a need for methods that offer theoretical justifications, rather than relying solely on empirical observations.
This paper introduces Credal Deep Ensembles (CreDEs), which predict probability intervals instead of single probabilities. This addresses the issue of uncertainty estimation by representing the uncertainty as a set of probabilities (credal set), which accounts for various possible data distributions. CreDEs show improved test accuracy, better calibration, and superior out-of-distribution detection compared to existing methods, demonstrating the effectiveness and robustness of the proposed approach.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel approach to uncertainty quantification in deep learning, addressing limitations of existing methods. CreDEs improve accuracy and calibration, providing more reliable predictions, especially in out-of-distribution scenarios. This is highly relevant to safety-critical applications and opens new avenues for research in robust AI and reliable uncertainty estimation.
Visual Insights#

This figure compares the proposed Credal Deep Ensembles (CreDEs) with traditional Deep Ensembles (DEs). CreDEs use Credal-Set Neural Networks (CreNets) that output probability intervals for each class, forming a credal set representing uncertainty. DEs, in contrast, use standard neural networks (SNNs) and average their single probability distribution outputs. The figure illustrates this difference using a probability simplex, showing how CreDEs’ interval predictions create a credal set (a region in the simplex) compared to DEs’ single-point predictions. The aggregation method for CreDEs is also briefly described.

This table presents the results of test accuracy and expected calibration error (ECE) for both Deep Ensembles (DEs) and Credal Deep Ensembles (CreDEs) on three image datasets (CIFAR10, CIFAR100, and ImageNet). The results are averaged over 15 independent runs and highlight the superior performance of CreDEs in terms of higher accuracy and lower ECE.
In-depth insights#
Credal Deep Ensembles#
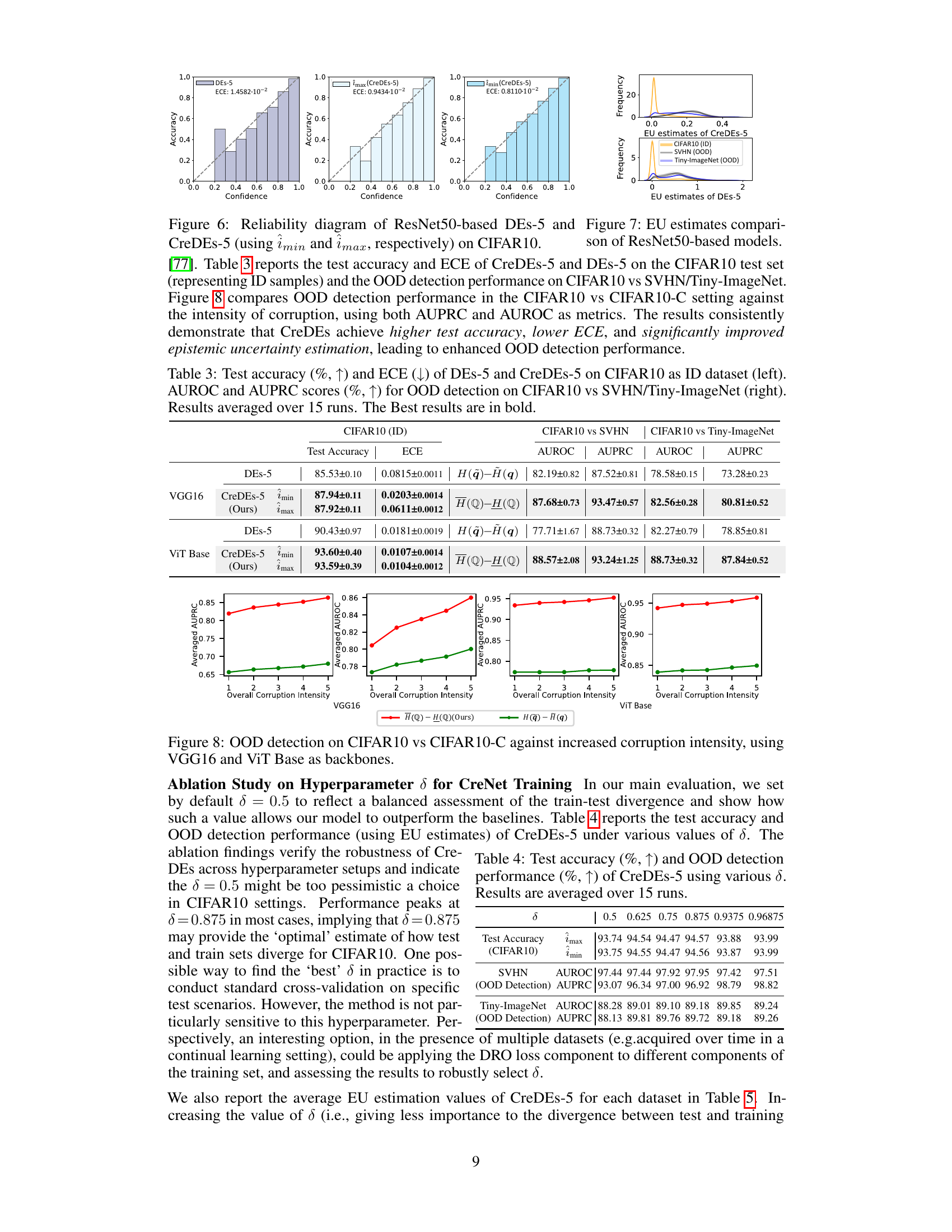
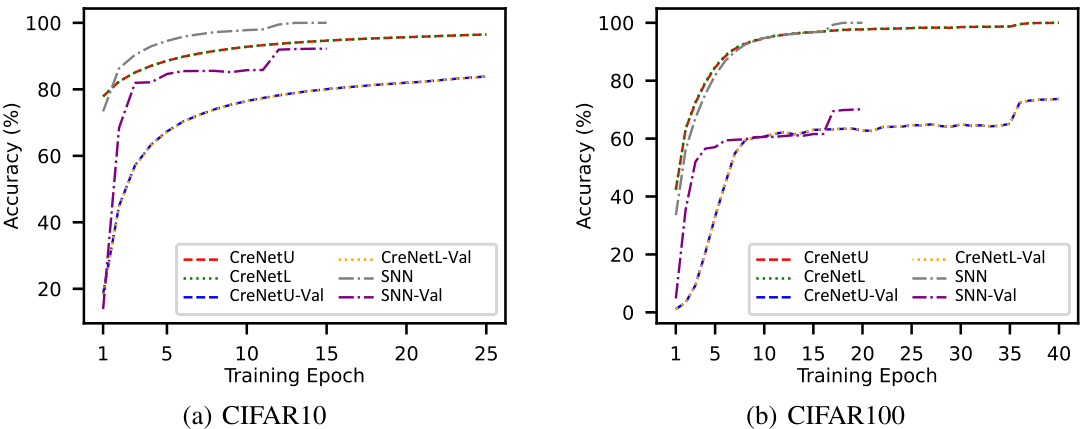
Credal Deep Ensembles (CreDEs) offer a novel approach to uncertainty quantification in deep learning. By predicting probability intervals instead of single probabilities, CreDEs address limitations of traditional methods like Deep Ensembles. The approach uses a loss function inspired by distributionally robust optimization, which helps the model account for potential divergence between training and test distributions. This leads to more robust uncertainty estimates, particularly valuable for out-of-distribution detection. CreDEs demonstrate improved performance in various benchmarks, achieving higher accuracy, lower expected calibration error, and better EU estimation. Combining this with ensemble methods strengthens the robustness and accuracy. However, further research is needed to address computational complexities and explore theoretical guarantees.
Epistemic Uncertainty#
Epistemic uncertainty, stemming from a lack of knowledge rather than inherent randomness, is a crucial consideration in machine learning. Deep ensembles, while popular for uncertainty quantification, often yield low-quality epistemic uncertainty estimates. The paper introduces Credal Deep Ensembles (CreDEs), which leverage Credal-Set Neural Networks (CreNets) to predict probability intervals instead of single probabilities, representing a credal set encompassing the uncertainty. This approach, inspired by distributionally robust optimization, directly addresses the potential divergence between training and test data distributions, providing a more robust measure of epistemic uncertainty. The training strategy effectively uses a composite loss, combining vanilla cross-entropy for the upper bound with a distributionally robust loss for the lower bound, capturing both optimistic and pessimistic perspectives on future data. Importantly, CreDEs demonstrate superior performance in uncertainty quantification compared to deep ensemble baselines across various benchmarks, highlighting their effectiveness in accurately reflecting epistemic uncertainty.
DRO Training#
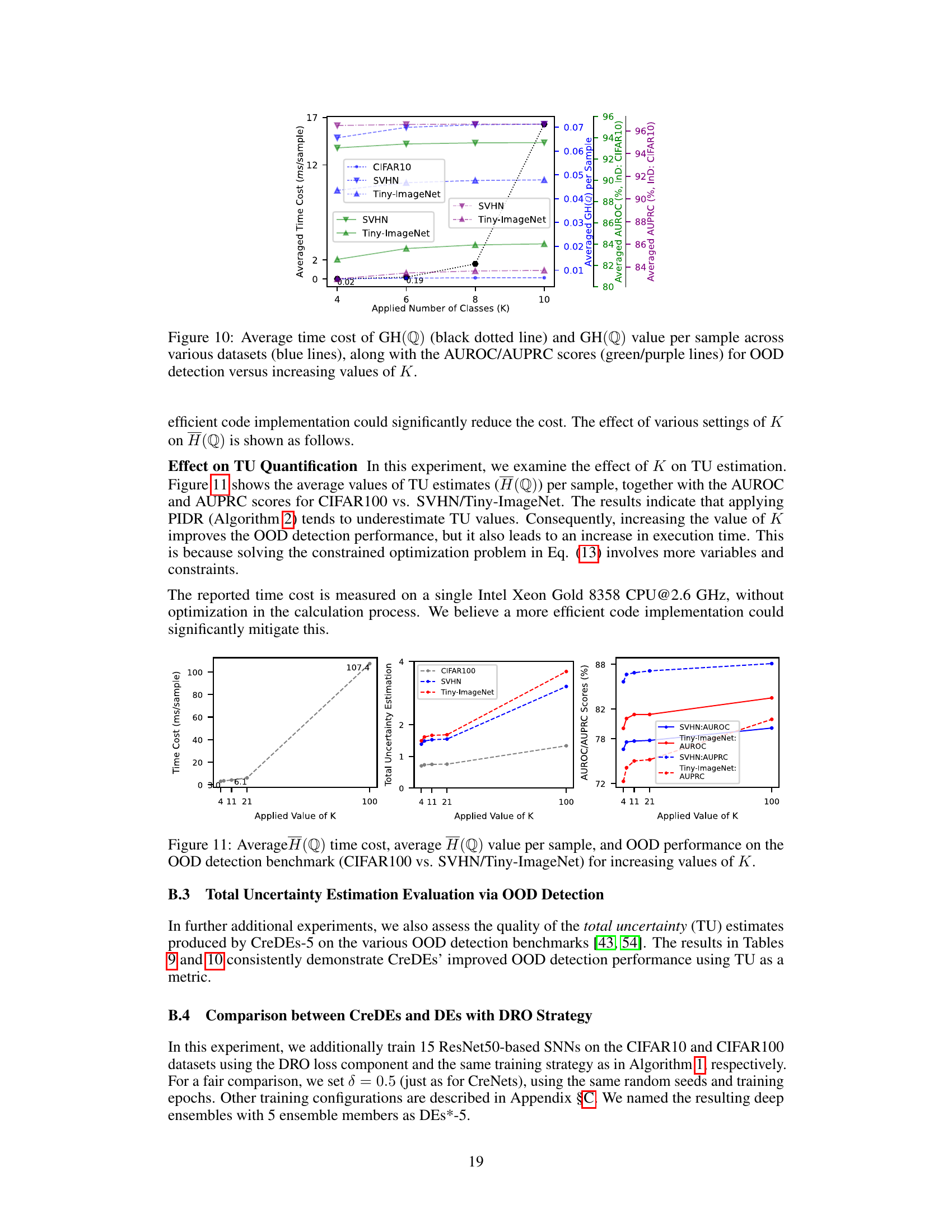
Distributionally Robust Optimization (DRO) training is a powerful technique to enhance the robustness of machine learning models, particularly deep learning models, by mitigating the effects of distributional shift between training and test data. DRO aims to minimize the worst-case risk, considering a set of possible data distributions. In contrast to standard empirical risk minimization, which assumes the training and test distributions are identical, DRO explicitly accounts for uncertainty in the test distribution. This makes the model more resilient to unseen data and less prone to overfitting on the training set. The effectiveness of DRO is demonstrated by improved generalization performance, especially in out-of-distribution (OOD) settings. It is particularly effective when dealing with data that is noisy or contains outliers, scenarios frequently encountered in real-world applications. However, the computational cost of DRO can be significantly higher than standard training methods, requiring careful consideration of the trade-off between robustness and computational efficiency. Different DRO formulations exist, each with its own advantages and limitations, necessitating careful selection based on the specific application and data characteristics.
OOD Detection#
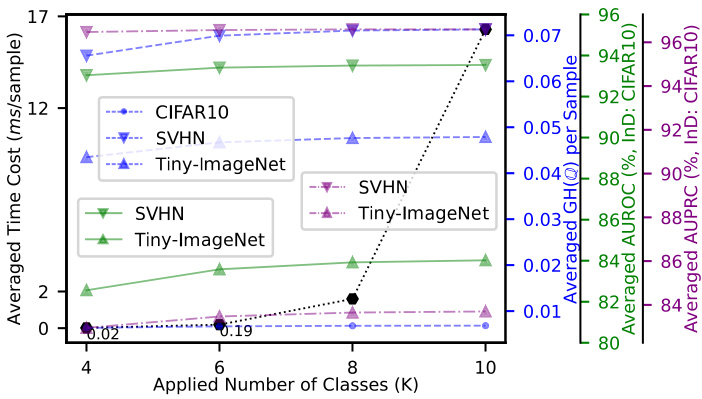
The research paper explores out-of-distribution (OOD) detection, a crucial aspect of ensuring reliable model performance. OOD detection is framed within the context of epistemic uncertainty quantification, arguing that models which better capture this type of uncertainty will also demonstrate improved OOD detection capabilities. The authors introduce a novel approach, Credal Deep Ensembles (CreDEs), that tackles OOD detection by producing probability intervals, effectively representing uncertainty using credal sets. This method is rigorously tested across multiple benchmarks using different network architectures and OOD scenarios. The results highlight CreDEs’ superiority over existing deep ensemble techniques, showing improved accuracy, better calibration, and significantly enhanced OOD detection performance. The key findings suggest a strong correlation between improved epistemic uncertainty quantification and robust OOD detection, establishing CreDEs as a promising solution for enhancing the reliability and robustness of deep learning models in real-world applications.
Future Works#
The paper’s “Future Works” section suggests several promising avenues for extending their research on Credal Deep Ensembles (CreDEs). Improving theoretical guarantees is crucial, as current CreDEs lack formal coverage guarantees. Exploring this through conformal prediction is a logical next step. Extending CreDEs to regression tasks is another key area, possibly leveraging random fuzzy sets to bridge the gap between credal sets and continuous probability distributions. Finally, the authors plan to conduct comprehensive real-world applications, moving beyond benchmark datasets to test the robustness and effectiveness of CreDEs in high-stakes domains. This involves further investigation into the generalized cross-entropy loss for improved uncertainty quantification, and a detailed exploration of different ensemble approaches beyond averaging, such as union and intersection methods. This holistic approach will solidify CreDEs’ capabilities and applicability in practical scenarios.
More visual insights#
More on figures
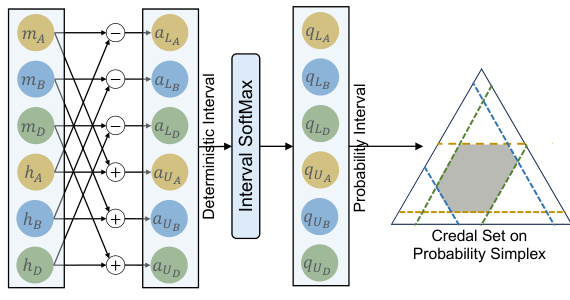
This figure illustrates the final layer structure of a Credal-Set Neural Network (CreNet) for three classes. The input vector z is passed to two sets of weight and bias matrices: W1:C, b1:C for calculating the interval midpoints (m) and WC+1:2C, bc+1:2C for calculating interval half-lengths (h). The Softplus function ensures non-negativity of h. The resulting deterministic intervals [al, au] are then passed through an Interval SoftMax activation function to produce probability intervals [qL, qU] which determine the final credal set on the probability simplex. The figure shows how the final probability intervals determine a credal set (gray shaded area) within the probability simplex.
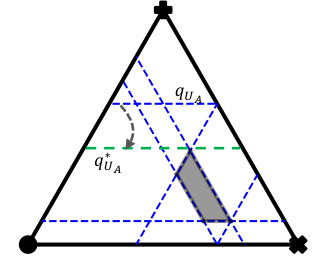
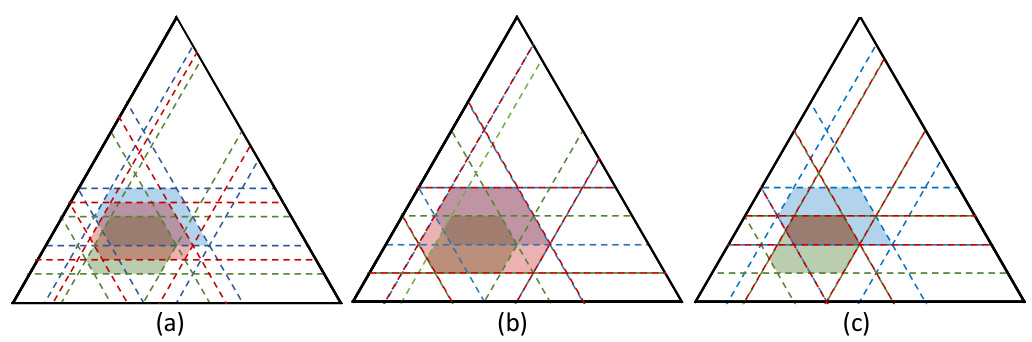
This figure illustrates a scenario in a three-class classification problem where the predicted probability intervals for each class ([qL, qU]) determine a credal set (a convex set of probability distributions). The figure highlights that due to redundancy, not all points within the theoretically possible region based on the intervals (the parallelogram) are actually feasible points within the resulting credal set (the shaded area). This is because the additional constraints imposed by the requirement that probabilities sum to 1, and must stay within the intervals, reduce the feasible region. The figure demonstrates that the actually reachable upper and lower probabilities might differ from the initially predicted probabilities.

This figure compares the proposed Credal Deep Ensembles (CreDEs) and traditional Deep Ensembles (DEs). CreDEs use CreNets that predict probability intervals representing credal sets, while DEs use standard SNNs that output single probability distributions. The figure illustrates how CreDEs aggregate credal sets to get the final prediction while DEs aggregate single probability distributions. It highlights the difference in prediction representation and aggregation between CreDEs and DEs.

This figure compares Credal Deep Ensembles (CreDEs) and traditional Deep Ensembles (DEs). CreDEs use Credal-Set Neural Networks (CreNets) that predict probability intervals for each class, forming a credal set representing the prediction uncertainty. DEs, conversely, use multiple standard neural networks (SNNs), averaging their individual probability distributions. The diagram illustrates how CreDEs aggregate credal sets (represented by the shaded areas within the probability simplex), while DEs average single probability vectors (points within the probability simplex).

This figure compares the proposed Credal Deep Ensembles (CreDEs) and traditional Deep Ensembles (DEs). CreDEs aggregate probability intervals from multiple Credal-Set Neural Networks (CreNets), representing a credal set. DEs average single probability distributions from standard neural networks (SNNs). The figure illustrates how CreNets predict probability intervals which define a credal set, and how these sets are aggregated to provide the final prediction in CreDEs.

This figure compares the proposed Credal Deep Ensembles (CreDEs) and traditional Deep Ensembles (DEs). CreDEs use Credal-Set Neural Networks (CreNets) which output probability intervals for each class, representing a credal set (convex set of probability distributions). DEs, on the other hand, use standard neural networks (SNNs) which output single probability distributions. The figure illustrates how CreDEs aggregate multiple credal sets to form a final credal prediction, while DEs average multiple single probability distributions. The probability simplex is used as a visual representation of the probability distributions.

This figure compares the proposed Credal Deep Ensembles (CreDEs) with traditional Deep Ensembles (DEs). CreDEs use Credal-Set Neural Networks (CreNets) that predict probability intervals for each class, forming a credal set. Traditional DEs average the predictions from multiple standard neural networks. The figure illustrates how CreDEs represent uncertainty as credal sets (shaded regions in the probability simplex) instead of single probability distributions (points in the simplex) as in DEs.
This figure compares Credal Deep Ensembles (CreDEs) and traditional Deep Ensembles (DEs). CreDEs use Credal-Set Neural Networks (CreNets) that output probability intervals for each class, forming a credal set. DEs average predictions from multiple standard neural networks (SNNs). The figure illustrates how CreDEs aggregate credal sets (represented as areas in the probability simplex), while DEs average single probability distributions (represented as points).

This figure compares the proposed Credal Deep Ensembles (CreDEs) and traditional Deep Ensembles (DEs). CreDEs use Credal-Set Neural Networks (CreNets) which predict probability intervals, representing a set of possible probability distributions (credal set), instead of single probability values like standard neural networks. The figure illustrates how the probability intervals from multiple CreNets are aggregated (averaged) to form the final credal prediction. In contrast, DEs average single probability distributions from multiple standard neural networks.
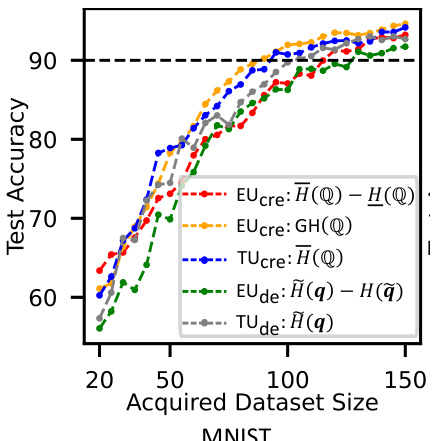
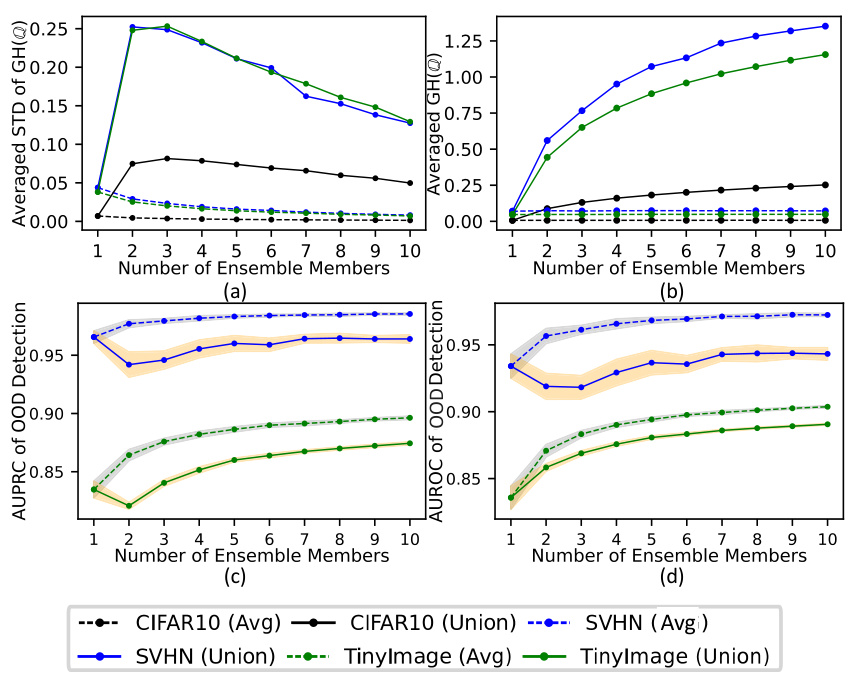
This figure compares the performance of active learning (AL) using different uncertainty measures for both CreDEs and DEs on the MNIST dataset. The x-axis represents the size of the acquired training dataset, and the y-axis represents the test accuracy achieved by the models. Multiple lines are shown, each corresponding to a different uncertainty measure (EU using both Shannon entropy and generalized Hartley measure for CreDEs, and TU and EU using Shannon entropy for DEs) used for sample selection in the AL process. The figure demonstrates how different uncertainty estimation methods affect the efficiency and effectiveness of active learning by showing how quickly the model’s test accuracy improves as more data is acquired during AL.
This figure compares Credal Deep Ensembles (CreDEs) and traditional Deep Ensembles (DEs). CreDEs use Credal-Set Neural Networks (CreNets) that output probability intervals for each class, forming a credal set (a set of probability distributions). DEs use standard neural networks (SNNs) that output single probability distributions. The figure illustrates how CreDEs aggregate interval predictions to create a final credal set prediction, while DEs average single probability distributions. The probability simplex visually represents the space of possible probability distributions for three classes.
This figure compares Credal Deep Ensembles (CreDEs) and traditional Deep Ensembles (DEs). CreDEs use Credal-Set Neural Networks (CreNets) that output probability intervals, which define a credal set (a set of probability distributions). These interval predictions are aggregated to form a final credal prediction. In contrast, DEs average single probability distributions from multiple individual neural networks. The figure illustrates these concepts using a probability simplex.
This figure compares the proposed Credal Deep Ensembles (CreDEs) and traditional Deep Ensembles (DEs). CreDEs use Credal-Set Neural Networks (CreNets) that predict probability intervals, forming a credal set representing uncertainty. DEs average predictions from multiple standard neural networks. The figure uses a probability simplex to illustrate how a single probability distribution is represented as a point, while CreDEs use intervals to define a region (credal set) representing uncertainty. The final CreDE prediction is an aggregate of multiple CreNet outputs.

This figure compares Credal Deep Ensembles (CreDEs) and traditional Deep Ensembles (DEs). CreDEs use Credal-Set Neural Networks (CreNets) that output probability intervals, representing a credal set (a set of probability distributions). DEs use standard neural networks (SNNs) that output single probability distributions. The figure illustrates how CreNets’ probability intervals form a credal set in the probability simplex, and how these credal sets are aggregated in CreDEs, as opposed to averaging single probability distributions in DEs.
More on tables

This table presents the test accuracy and Expected Calibration Error (ECE) for both Deep Ensembles (DEs-5) and Credal Deep Ensembles (CreDEs-5) on three image classification datasets (CIFAR-10, CIFAR-100, and ImageNet). The results are averaged over 15 independent runs, each starting from a different random seed. Higher test accuracy and lower ECE indicate better performance. Bold values show where CreDEs-5 outperforms DEs-5.

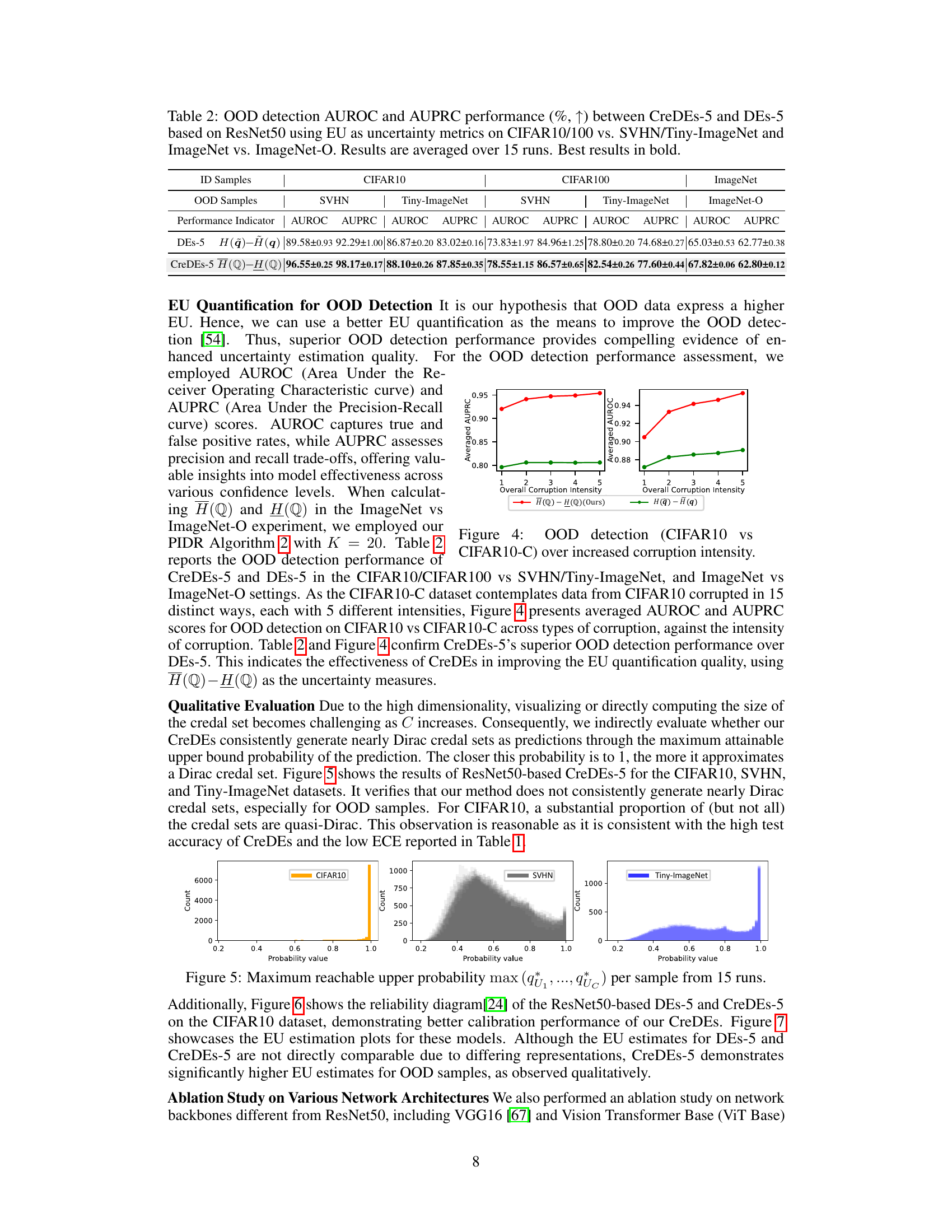
This table presents the results of out-of-distribution (OOD) detection experiments comparing Credal Deep Ensembles (CreDEs) and Deep Ensembles (DEs). The Area Under the Receiver Operating Characteristic curve (AUROC) and Area Under the Precision-Recall Curve (AUPRC) are reported for various dataset pairs (CIFAR10/100 vs. SVHN/Tiny-ImageNet, and ImageNet vs. ImageNet-O). The results are based on ResNet50 architecture, using Epistemic Uncertainty (EU) as the uncertainty metric, and averaged over 15 runs. The best performing model for each metric and dataset pair is shown in bold.

This table presents the results of comparing the performance of Deep Ensembles (DEs) and Credal Deep Ensembles (CreDEs) on three image classification datasets: CIFAR10, CIFAR100, and ImageNet. The metrics used are test accuracy (higher is better) and Expected Calibration Error (ECE) (lower is better). The results are averaged over 15 independent runs, and the best performing model for each metric and dataset is highlighted in bold. The table demonstrates the improved performance of CreDEs in terms of both accuracy and ECE compared to the standard DE baseline.

This table presents the results of the test accuracy and expected calibration error (ECE) for both Deep Ensembles (DEs) and Credal Deep Ensembles (CreDEs) on three image datasets: CIFAR10, CIFAR100, and ImageNet. The results are averaged over 15 runs with different random seeds, and the better performance (higher accuracy and lower ECE) is highlighted in bold. This table demonstrates the improved performance of CreDEs over the baseline DEs in terms of accuracy and calibration.

This table presents a comparison of the test accuracy and expected calibration error (ECE) between Deep Ensembles (DEs) and Credal Deep Ensembles (CreDEs) on three image datasets (CIFAR-10, CIFAR-100, and ImageNet). The results are averaged over 15 independent runs, and the best performing model for each metric is highlighted in bold. It demonstrates CreDEs’ superior performance in terms of both accuracy and calibration.

This table presents the results of testing the performance of Deep Ensembles (DEs) and Credal Deep Ensembles (CreDEs) on three image datasets (CIFAR10, CIFAR100, and ImageNet). The metrics used to evaluate performance are test accuracy (higher is better) and Expected Calibration Error (ECE) (lower is better). The results are averaged across 15 runs for both methods, and the best-performing method for each metric and dataset is shown in bold.

This table presents the Area Under the Receiver Operating Characteristic curve (AUROC) and the Area Under the Precision-Recall Curve (AUPRC) for out-of-distribution (OOD) detection. It compares the performance of Credal Deep Ensembles (CreDEs) with 5 models (CreDEs-5) against Deep Ensembles (DEs) with 5 models (DEs-5). The results are obtained using ResNet50 architecture and the epistemic uncertainty (EU) as the uncertainty metric. The experiment is run 15 times with different random seeds, and the average performance and standard deviation are reported. The comparison is done across different dataset pairings: CIFAR10/CIFAR100 vs. SVHN/Tiny-ImageNet and ImageNet vs. ImageNet-O. The best performance for each metric and dataset is shown in bold.

This table presents the results of out-of-distribution (OOD) detection experiments using Credal Deep Ensembles (CreDEs) and Deep Ensembles (DEs) as baselines. The experiments were conducted on four different dataset pairings: CIFAR10/CIFAR100 vs. SVHN/Tiny-ImageNet, and ImageNet vs. ImageNet-O. The performance is evaluated using the Area Under the Receiver Operating Characteristic curve (AUROC) and the Area Under the Precision-Recall curve (AUPRC) metrics. Epistemic Uncertainty (EU), calculated as H(Q)-H(Q), is used as the uncertainty measure. The table shows that CreDEs consistently outperforms DEs across all datasets and metrics.

This table presents the Area Under the Receiver Operating Characteristic (AUROC) and Area Under the Precision-Recall Curve (AUPRC) scores for out-of-distribution (OOD) detection. It compares the performance of Credal Deep Ensembles (CreDEs) with 5 models (CreDEs-5) against Deep Ensembles (DEs) with 5 models (DEs-5). The results are obtained using ResNet50 models and the EU (epistemic uncertainty) metric. The experiments were run 15 times, and the average results are presented. The table shows the performance on various datasets: CIFAR10/100 (in-distribution) versus SVHN/Tiny-ImageNet (out-of-distribution), and ImageNet (in-distribution) versus ImageNet-O (out-of-distribution).

This table presents the results of out-of-distribution (OOD) detection experiments using Credal Deep Ensembles (CreDEs) and Deep Ensembles (DEs) as baselines. The Area Under the Receiver Operating Characteristic curve (AUROC) and Area Under the Precision-Recall curve (AUPRC) are reported for four different dataset pairings: CIFAR-10/CIFAR-100 vs. SVHN/Tiny-ImageNet, and ImageNet vs. ImageNet-O. The results are based on ResNet50 architectures and averaged over 15 runs, with the best results highlighted in bold. The EU metric (epistemic uncertainty) is used for uncertainty quantification.

This table presents the results of comparing Deep Ensembles (DEs) and Credal Deep Ensembles (CreDEs) on three image classification datasets (CIFAR10, CIFAR100, and ImageNet). It shows the test accuracy and Expected Calibration Error (ECE) for both methods. Higher accuracy and lower ECE indicate better model performance. The results are averaged over 15 independent runs for each method. Bold values highlight the superior performance between DEs and CreDEs on each metric.
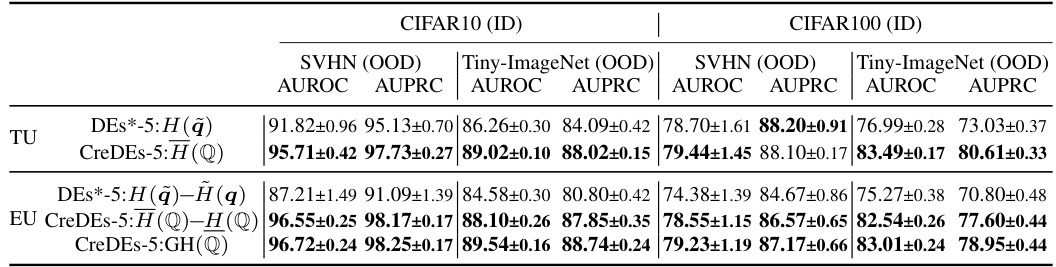
This table presents the results of out-of-distribution (OOD) detection experiments using two different ensemble methods: Credal Deep Ensembles (CreDEs) and Deep Ensembles (DEs). The experiments were performed using the ResNet50 architecture on four different dataset pairs. The table shows the Area Under the Receiver Operating Characteristic curve (AUROC) and the Area Under the Precision-Recall Curve (AUPRC) for each ensemble method and dataset pair. Higher AUROC and AUPRC values indicate better OOD detection performance. The results are averaged across 15 runs, and the best result for each metric and dataset pair is highlighted in bold. The uncertainty metric used is Epistemic Uncertainty (EU).
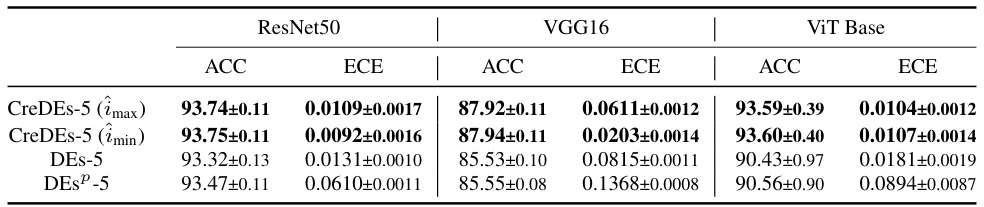
This table presents the test accuracy and expected calibration error (ECE) for both Deep Ensembles (DEs) and Credal Deep Ensembles (CreDEs) on three image classification datasets (CIFAR10, CIFAR100, and ImageNet). The results are averaged over 15 independent runs, and the best performing model (CreDEs-5) is highlighted in bold. It demonstrates CreDEs’ superior performance in terms of accuracy and calibration.

This table presents the Area Under the Receiver Operating Characteristic curve (AUROC) and the Area Under the Precision-Recall Curve (AUPRC) for out-of-distribution (OOD) detection. It compares the performance of Credal Deep Ensembles (CreDEs) with 5 models (CreDEs-5) against Deep Ensembles (DEs) with 5 models (DEs-5), using ResNet50 architecture and the epistemic uncertainty (EU) as the uncertainty metric. The results are averaged over 15 runs with different random seeds and presented for different dataset pairings: CIFAR10/CIFAR100 (in-distribution) versus SVHN/Tiny-ImageNet (out-of-distribution), and ImageNet (in-distribution) versus ImageNet-O (out-of-distribution). The best-performing method for each metric and dataset is highlighted in bold.
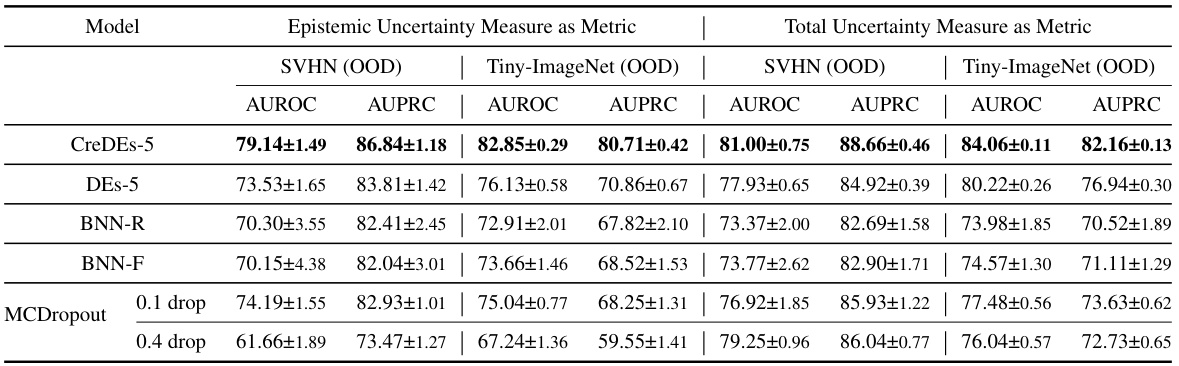
This table presents the results of out-of-distribution (OOD) detection experiments using two different ensemble methods: Credal Deep Ensembles (CreDEs) and Deep Ensembles (DEs). The experiments were performed using the ResNet50 architecture, with epistemic uncertainty (EU) as the metric for evaluating OOD detection performance. The table shows AUROC (Area Under the Receiver Operating Characteristic curve) and AUPRC (Area Under the Precision-Recall curve) scores for different dataset pairings: CIFAR10/100 (in-distribution) versus SVHN/Tiny-ImageNet (out-of-distribution), and ImageNet (in-distribution) versus ImageNet-O (out-of-distribution). The results are averages across 15 runs, and the best-performing method for each metric and dataset pair is highlighted in bold.

This table presents a comparison of the performance of Deep Ensembles (DEs) and Credal Deep Ensembles (CreDEs) on three image classification datasets (CIFAR10, CIFAR100, and ImageNet). The metrics used are test accuracy (higher is better) and Expected Calibration Error (ECE) (lower is better). Results are averaged over 15 independent runs, and the best performing method for each metric on each dataset is highlighted in bold. This helps to demonstrate the improved accuracy and calibration of CreDEs compared to the baseline DEs.

This table presents a comparison of the test accuracy and Expected Calibration Error (ECE) for Deep Ensembles (DEs) and Credal Deep Ensembles (CreDEs) on three image classification datasets (CIFAR-10, CIFAR-100, and ImageNet). The results are averaged over 15 independent runs, each starting with a different random seed. Bold values indicate superior performance for CreDEs.
Full paper#