↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many deep learning phenomena are affected by parameter symmetries—transformations of neural network parameters that do not change the underlying function. However, the relationship between these symmetries and various deep learning behaviors remains poorly understood. This lack of understanding hinders the development of more efficient and interpretable neural networks.
This paper empirically investigates the effects of neural parameter symmetries by introducing new neural network architectures with reduced symmetries. The authors developed two methods—W-Asymmetric and σ-Asymmetric networks—to reduce symmetries. Extensive experiments show that removing these symmetries leads to significant improvements in various aspects, including faster Bayesian neural network training and improved linear interpolation behavior. The findings challenge the prevailing understanding of neural network loss landscapes and suggest that reducing symmetries could be a key factor in developing more efficient and interpretable deep learning models.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in deep learning as it empirically investigates the often-overlooked impact of neural network parameter symmetries. It introduces novel methods for reducing these symmetries and presents compelling experimental results demonstrating improved optimization, generalization, and interpretability. This opens new avenues for understanding and designing more efficient and robust neural network architectures.
Visual Insights#
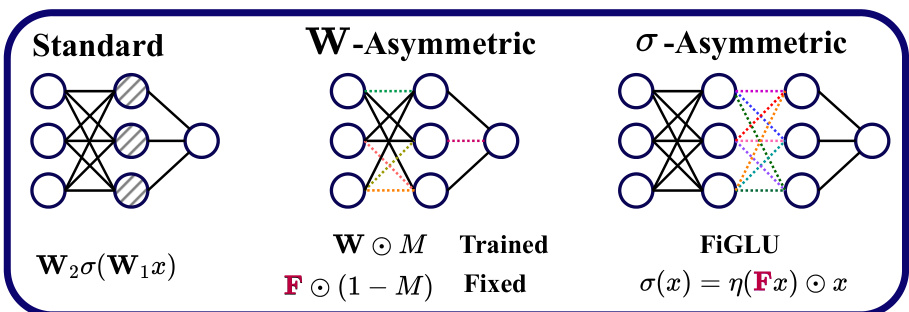
This figure illustrates the three types of MLPs used in the paper: standard MLPs, W-Asymmetric MLPs, and σ-Asymmetric MLPs. Standard MLPs have hidden nodes that are fully interchangeable, leading to permutation symmetries. W-Asymmetric MLPs break these symmetries by fixing some weights to be constant and non-trainable. σ-Asymmetric MLPs use a different nonlinearity called FiGLU, which also helps to remove symmetries. The figure uses color-coding to distinguish trainable parameters (black) from fixed parameters (colored dashed lines).

This table presents the results of an experiment measuring the test loss interpolation barriers at the midpoint of linear interpolation between two trained neural networks. The experiment compares four different methods: standard networks, networks aligned using Git-Rebasin, σ-Asymmetric networks, and W-Asymmetric networks. Each method’s performance is evaluated across multiple network architectures and datasets, reporting the mean and standard deviation of the loss barrier. Lower values indicate better interpolation performance, suggesting a more linearly-connected loss landscape.
In-depth insights#
Neural Symmetries#
The concept of “Neural Symmetries” in deep learning refers to transformations of a neural network’s parameters that leave its function unchanged. These symmetries, often stemming from architectural properties (like the permutable order of neurons in a layer), introduce redundancy in the parameter space. The paper investigates the empirical consequences of these symmetries, exploring how they affect various aspects of neural networks. Removing or reducing these symmetries, through architectural modifications, is shown to lead to several key improvements. This includes better linear mode connectivity (smoother loss landscapes), improved Bayesian neural network training (faster convergence), and more accurate predictions by metanetworks that evaluate network performance. The core finding highlights that the presence of symmetries can mask inherent complexities in the loss landscape, leading to suboptimal training dynamics. Understanding and controlling these symmetries is crucial for advancing our comprehension of neural network training and generalization.
Asymmetric Nets#
The core concept of “Asymmetric Nets” revolves around mitigating the effects of parameter symmetries in neural networks. Standard networks often exhibit redundancies where multiple parameter sets yield the same network function. This paper introduces methods to break these symmetries, creating W-Asymmetric nets (modifying weight matrices to remove symmetries) and σ-Asymmetric nets (employing novel nonlinearities). The key insight is that reducing symmetries can lead to better generalization, improved optimization, and more well-behaved loss landscapes. The study’s empirical results showcase improved interpolation, faster Bayesian training, and more accurate metanetwork predictions on Asymmetric Networks compared to standard ones, highlighting their potential for enhancing neural network training and performance. The theoretical justifications and empirical findings collectively suggest a fundamental shift in neural network design by strategically reducing the inherent redundancies.
Linear Mode Con#
The concept of “Linear Mode Connectivity” (LMC) in neural networks explores the landscape of model performance during linear interpolation between two independently trained models. Standard networks often exhibit poor performance in the interpolation region, suggesting a non-convex loss landscape. This research investigates whether breaking neural network parameter symmetries can improve LMC. The study introduces novel architectures (W-Asymmetric and σ-Asymmetric networks) designed to reduce these symmetries, resulting in a more linear and well-behaved interpolation. W-Asymmetric networks show particularly strong LMC, often surpassing even methods that explicitly align the parameter spaces of two networks before interpolation. This improvement indicates that parameter symmetries significantly contribute to the non-convexity of the loss landscape and hindering LMC. The findings suggest that addressing symmetries is crucial for creating more robust and predictable neural network training and optimization processes.
Bayesian NN Boost#
The heading ‘Bayesian NN Boost’ suggests a research focus on improving Bayesian neural networks. This likely involves tackling the challenges associated with Bayesian neural networks, such as the high computational cost of inference and the difficulty in approximating the posterior distribution. The research might explore novel architectures or training methods specifically designed to enhance the efficiency and accuracy of Bayesian neural network training. This could involve techniques like variational inference with improved approximating families, more efficient sampling methods, or novel network architectures that inherently reduce the complexity of the posterior. The ‘boost’ aspect implies a significant performance improvement over existing Bayesian neural network approaches, potentially through faster training times, higher accuracy, or better calibration. The research could also investigate the effect of reducing parameter symmetries in Bayesian neural networks, as symmetries often lead to difficulties in model identifiability and posterior estimation. Overall, a ‘Bayesian NN Boost’ study would offer valuable contributions to the field by making Bayesian deep learning more practical and accessible for real-world applications.
Future Directions#
Future research could explore the theoretical underpinnings of asymmetric networks more rigorously, perhaps by developing a more comprehensive understanding of how they affect loss landscapes and optimization dynamics. Investigating the impact of asymmetry on generalization, robustness, and adversarial attacks would also be valuable. The empirical success of the proposed methods suggests further investigation into specific applications, such as Bayesian neural networks and metanetworks, is warranted. It would be interesting to explore different strategies for introducing asymmetry, beyond the methods presented, and to investigate the interplay between different types of symmetries and their removal. Finally, a more detailed investigation of the relationship between the degree of asymmetry and training time/convergence rates is needed to improve efficiency.
More visual insights#
More on figures

This figure illustrates the W-Asymmetric approach to reduce parameter space symmetries in neural networks. It shows how this method modifies standard and convolutional layers by fixing some of the weights (black outlined entries). The linear layer has 2 non-zero entries per row, the fixed-entry convolutional layer has 8 fixed entries, and the fixed-filter convolutional layer has one fixed input filter. The number of fixed entries is a hyperparameter that can be adjusted during experiments.
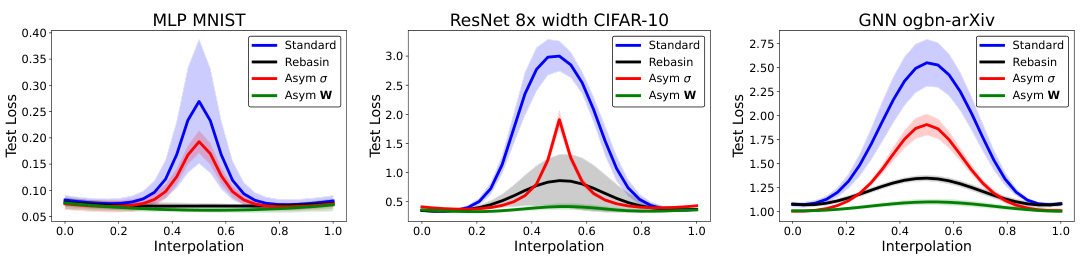
This figure displays test loss curves for linear interpolations between two trained neural networks. The interpolation is done by linearly combining the weights of the two networks. Three different network architectures are shown: MLP (Multilayer Perceptron) on the MNIST dataset, ResNet (Residual Network) with 8x width on CIFAR-10, and GNN (Graph Neural Network) on the ogbn-arXiv dataset. The results demonstrate that W-Asymmetric networks show the best interpolation performance (lowest loss during interpolation), followed by networks whose weights have been aligned using the Git-Rebasin method. σ-Asymmetric networks perform better than standard networks, but worse than the others.
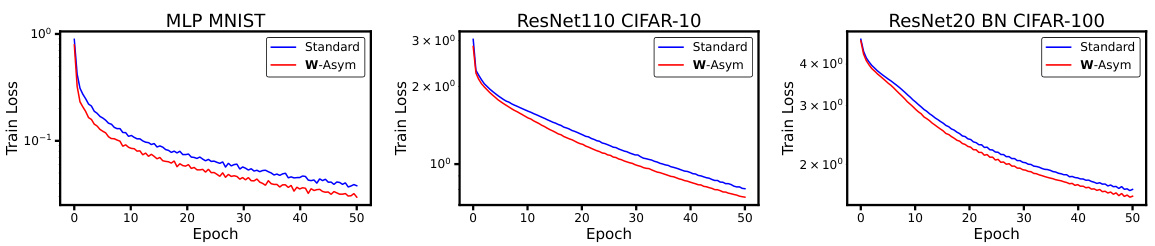
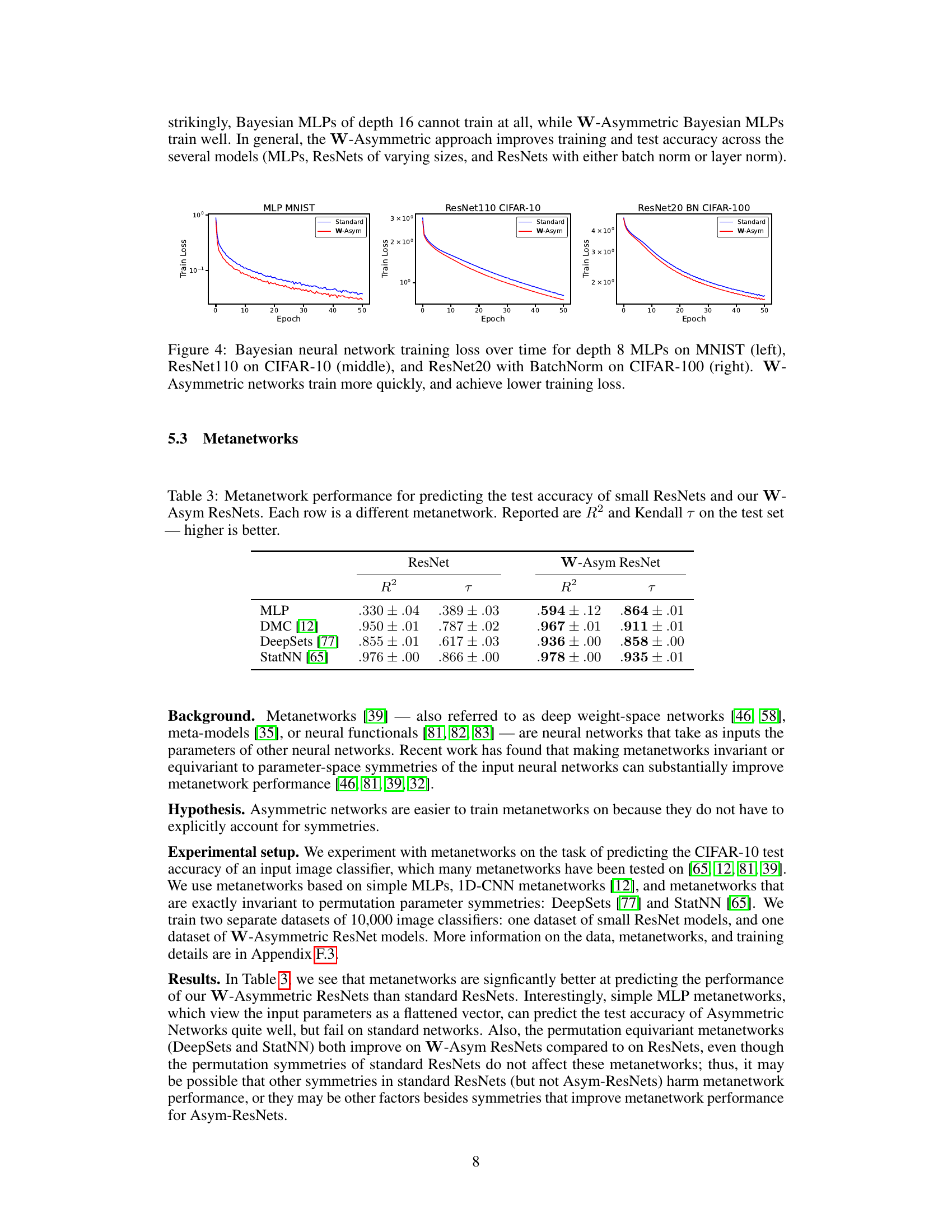
This figure shows training loss curves for standard and W-Asymmetric Bayesian neural networks across three different datasets and architectures: MNIST with depth 8 MLPs, CIFAR-10 with ResNet110, and CIFAR-100 with ResNet20 with Batch Normalization. The results demonstrate that W-Asymmetric networks consistently achieve lower training loss and faster convergence than their standard counterparts.

This figure shows the test loss curves for linear interpolation between two independently trained networks for three different network architectures (MLP, ResNet, and GNN) and datasets (MNIST, CIFAR-10, and ogbn-arXiv). The x-axis represents the interpolation coefficient, ranging from 0 (first network) to 1 (second network). The y-axis shows the test loss. The figure demonstrates that W-Asymmetric networks exhibit the best linear mode connectivity (smooth interpolation with low loss), followed by networks aligned using the Git-Rebasin method, then σ-Asymmetric networks, and lastly standard networks. This highlights the improved loss landscape properties of Asymmetric networks.

This figure shows the effect of varying hyperparameters on training time for W-Asymmetric ResNets on CIFAR-10. The hyperparameters are the number of fixed entries (nfix) and the standard deviation (κ) of the fixed entries. As the number of fixed entries increases and the standard deviation increases, the networks become more asymmetric and require significantly more epochs to reach 70% training accuracy. The heatmap visually represents this relationship.
More on tables
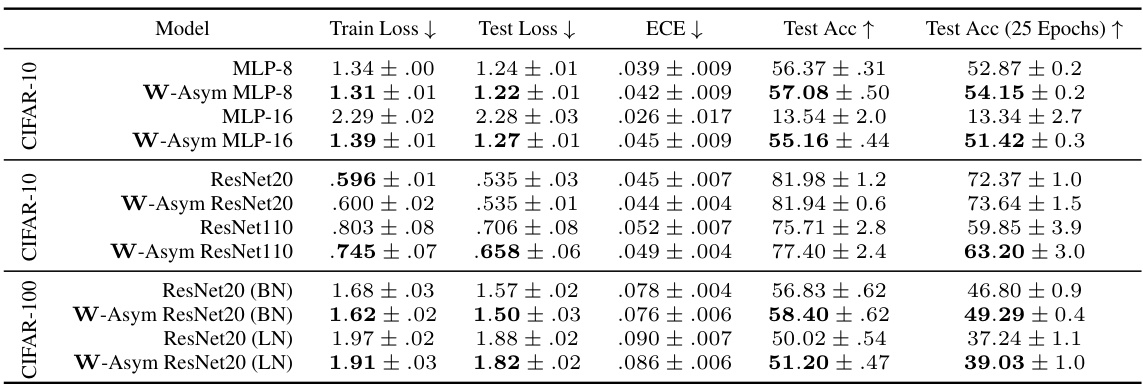
This table presents the results of experiments comparing standard and asymmetric Bayesian neural networks on various datasets and architectures. It shows that W-Asymmetric networks generally achieve lower training loss, lower expected calibration error (ECE), and higher test accuracy, particularly noticeable in the early training stages. The table also highlights that 16-layer standard MLPs fail to train, while their W-Asymmetric counterparts succeed. Results that are statistically significantly better than the corresponding standard models are bolded.
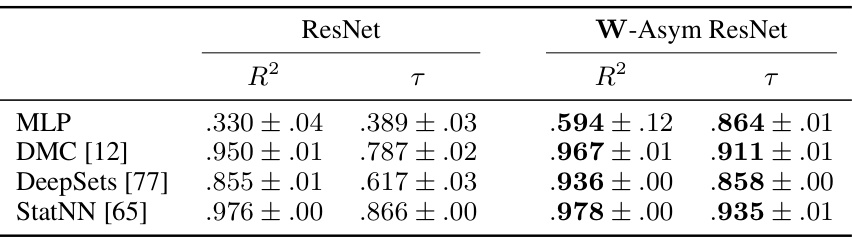
This table presents the performance of four different metanetworks in predicting the test accuracy of two types of ResNet models: standard ResNets and W-Asymmetric ResNets. The metanetworks used are MLP, DMC, DeepSets, and StatNN. The R-squared (R2) and Kendall’s tau (τ) correlation coefficients are reported, indicating the strength of the correlation between the metanetwork’s prediction and the actual test accuracy. Higher values for both metrics are better, implying stronger predictive power.

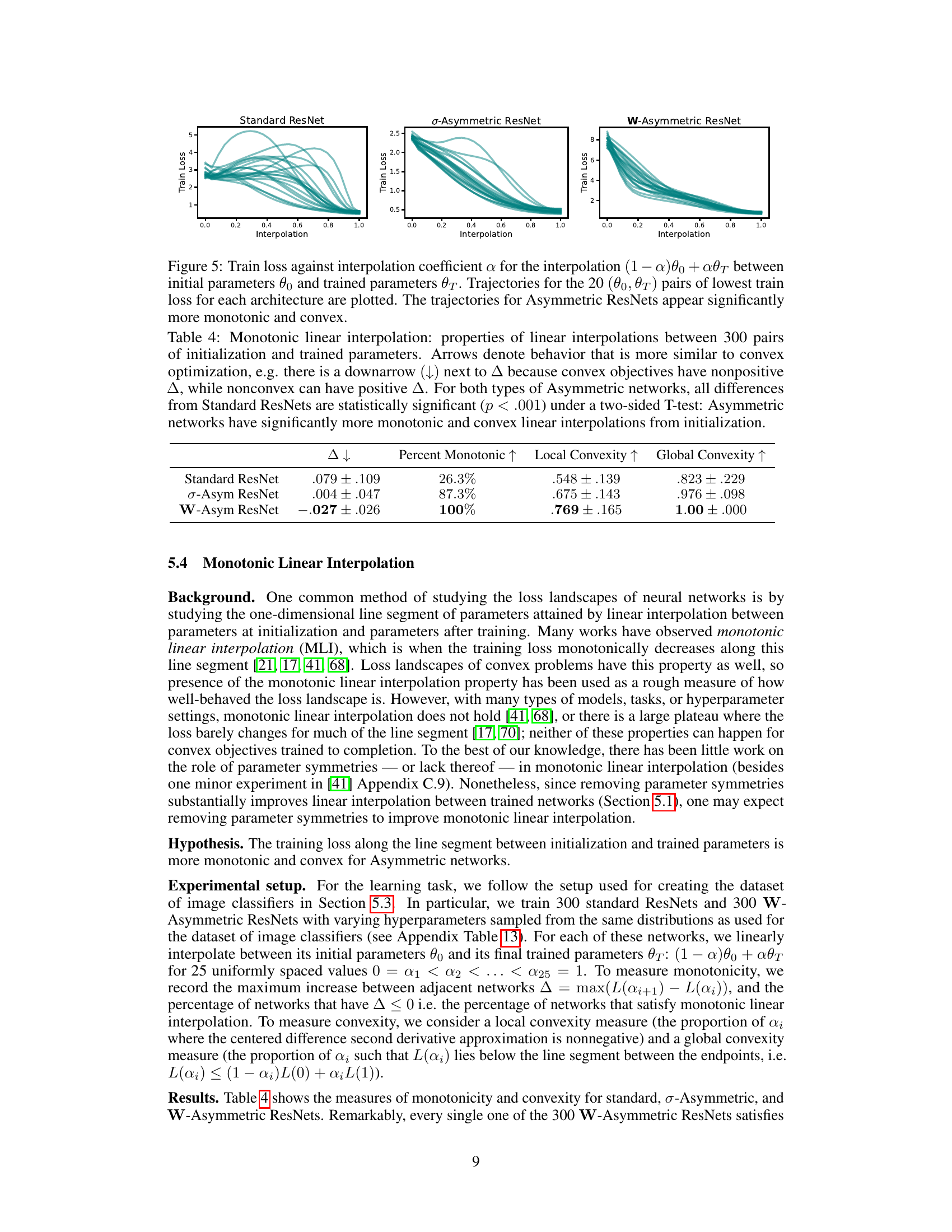
This table presents the results of an experiment evaluating monotonic linear interpolation (MLI) in different neural network architectures. Three types of networks are compared: standard ResNets, σ-Asymmetric ResNets, and W-Asymmetric ResNets. The table shows the mean and standard deviation of four key metrics across 300 pairs of networks: the maximum increase in loss (Δ), the percentage of monotonic interpolations, local convexity, and global convexity. The results demonstrate that Asymmetric networks exhibit significantly better MLI properties, indicating smoother and more convex loss landscapes compared to standard ResNets.

This table shows the results of an experiment measuring the test loss interpolation barrier at the midpoint for different methods of breaking parameter symmetries in neural networks. The experiment compares standard networks, networks aligned using Git-Rebasin, σ-Asymmetric networks, and W-Asymmetric networks. The mean and standard deviation of the loss barrier are reported for each method across multiple pairs of networks, highlighting the lowest barrier values.
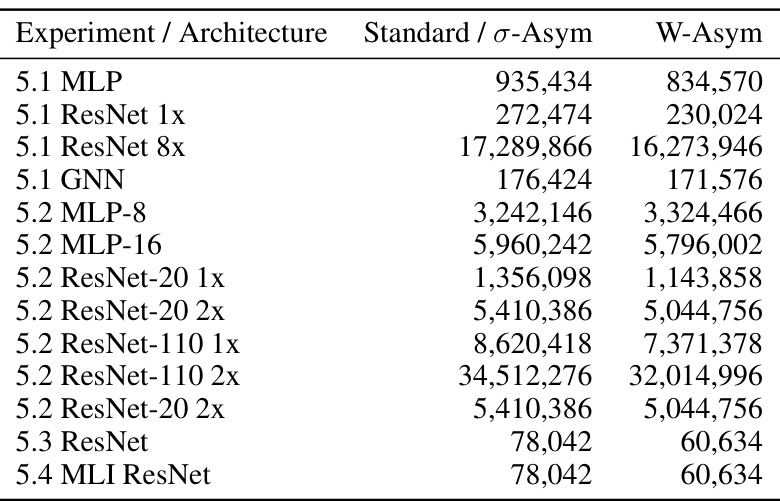
This table presents the number of trainable parameters for different neural network architectures used in the experiments. It compares the number of learnable parameters in standard networks to those in the W-Asymmetric and σ-Asymmetric versions. The reduction in parameters in the asymmetric networks is a result of fixing certain parameters to break parameter symmetries.

This table presents the performance of several metanetworks in predicting the test accuracy of small ResNets and W-Asymmetric ResNets. The metanetworks tested include simple MLPs, DMC, DeepSets, and StatNN. The R-squared (R2) and Kendall’s tau (τ) correlation coefficients are reported, with higher values indicating better predictive performance. The table aims to demonstrate that W-Asymmetric ResNets are easier for metanetworks to accurately predict performance for, likely due to the removal of parameter symmetries.

This table presents the results of Bayesian Neural Network (BNN) experiments on CIFAR-10, comparing the test accuracy of W-Asymmetric ResNet20, Standard ResNet20, and a Smaller Standard ResNet20 (with the number of parameters reduced to match W-Asym ResNet20). The goal is to investigate whether the improved performance of the Asymmetric networks in Bayesian setting is due to the reduced number of parameters or due to the removal of parameter symmetries. The table shows that the test accuracy of W-Asymmetric ResNet20 remains higher even after adjusting the number of parameters in the standard ResNet20 model, suggesting that the removal of parameter symmetries plays a significant role in the improved performance.

This table presents the results of an experiment measuring the test loss barrier for linear interpolation between two independently trained networks (ResNet20 on CIFAR-10 and GNN on ogbn-arXiv). The experiment varies the number of warmup epochs used during training (1 versus 20). The table compares the test loss barrier for standard networks, networks aligned using the Git-Rebasin method, σ-Asymmetric networks, and W-Asymmetric networks. The results show that W-Asymmetric networks consistently exhibit lower test loss barriers, indicating better interpolation performance, regardless of the number of warmup steps.

This table presents the results of an experiment comparing the test loss interpolation barriers of four different methods for breaking symmetries in neural networks. The methods are: no symmetry breaking, Git-Rebasin, σ-Asymmetric approach, and W-Asymmetric approach. The table shows the mean and standard deviation of the test loss interpolation barrier for each method across at least 5 pairs of networks. The lowest barriers are shown in bold.
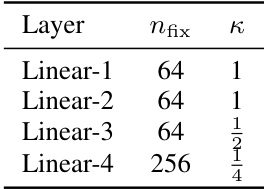
This table shows the hyperparameters used for the four-layer Multilayer Perceptron (MLP) experiments in the paper. Specifically, it details the number of randomly fixed weights (nfix) and the standard deviation (κ) of the normal distribution from which the fixed weights (F) are sampled for each of the four linear layers in the MLP. The values of nfix and κ influence the degree of asymmetry introduced into the network architecture.

This table presents the results of an experiment measuring the test loss interpolation barriers at the midpoint for four different methods: no symmetry breaking, Git-Rebasin, σ-Asymmetric, and W-Asymmetric. The mean and standard deviation are reported for each method across at least 5 pairs of networks. The lowest barriers for each method are highlighted in bold. The table aims to show how different methods of removing parameter symmetries in neural networks affect the performance of linear interpolation between trained networks.
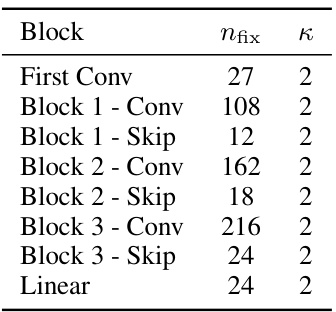
This table shows the hyperparameters used for the W-Asymmetric ResNet20 model with a width multiplier of 8, trained on the CIFAR-10 dataset. It specifies the number of fixed entries (nfix) and the standard deviation (κ) of the normal distribution from which the fixed entries are sampled for each block of the network (consisting of convolutional and skip layers). These hyperparameters control the level of asymmetry introduced into the network.

This table presents the results of Bayesian neural network experiments using both standard and asymmetric network architectures. It compares training and test loss, expected calibration error (ECE), and test accuracy across various network depths and configurations (MLPs and ResNets). The results show that W-Asymmetric networks often achieve better performance, particularly faster training convergence and improved accuracy.

This table presents the performance of four different metanetworks in predicting the test accuracy of two types of ResNet models: standard ResNets and W-Asymmetric ResNets. The metanetworks used are MLP, DMC, DeepSets, and StatNN. The R-squared (R2) and Kendall’s Tau (τ) correlation coefficients are reported for each metanetwork and model type, providing a measure of how well each metanetwork predicts the test accuracy.
Full paper#