↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Training large language models (LLMs) requires significant computational resources. Sharded Data Parallelism (SDP) is a common approach to distribute training across multiple GPUs, but it suffers from high communication overheads due to the exchange of massive weight and gradient updates. Existing compression techniques often compromise accuracy.
The proposed method, SDP4Bit, tackles this issue by using two novel quantization techniques: quantizing weight differences instead of weights directly, and employing a two-level gradient smooth quantization. The results show that SDP4Bit effectively reduces communication to nearly 4 bits while maintaining training accuracy and achieving up to 4.08x speedup on a 128-GPU setup, making it a very promising approach for accelerating LLM training.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on large language model (LLM) training. It directly addresses the scalability challenges of Sharded Data Parallelism (SDP) by introducing a novel communication reduction strategy. The significant speedup achieved (up to 4.08x) and the theoretical convergence guarantees make it highly relevant to current research trends and open new avenues for optimizing distributed LLM training.
Visual Insights#

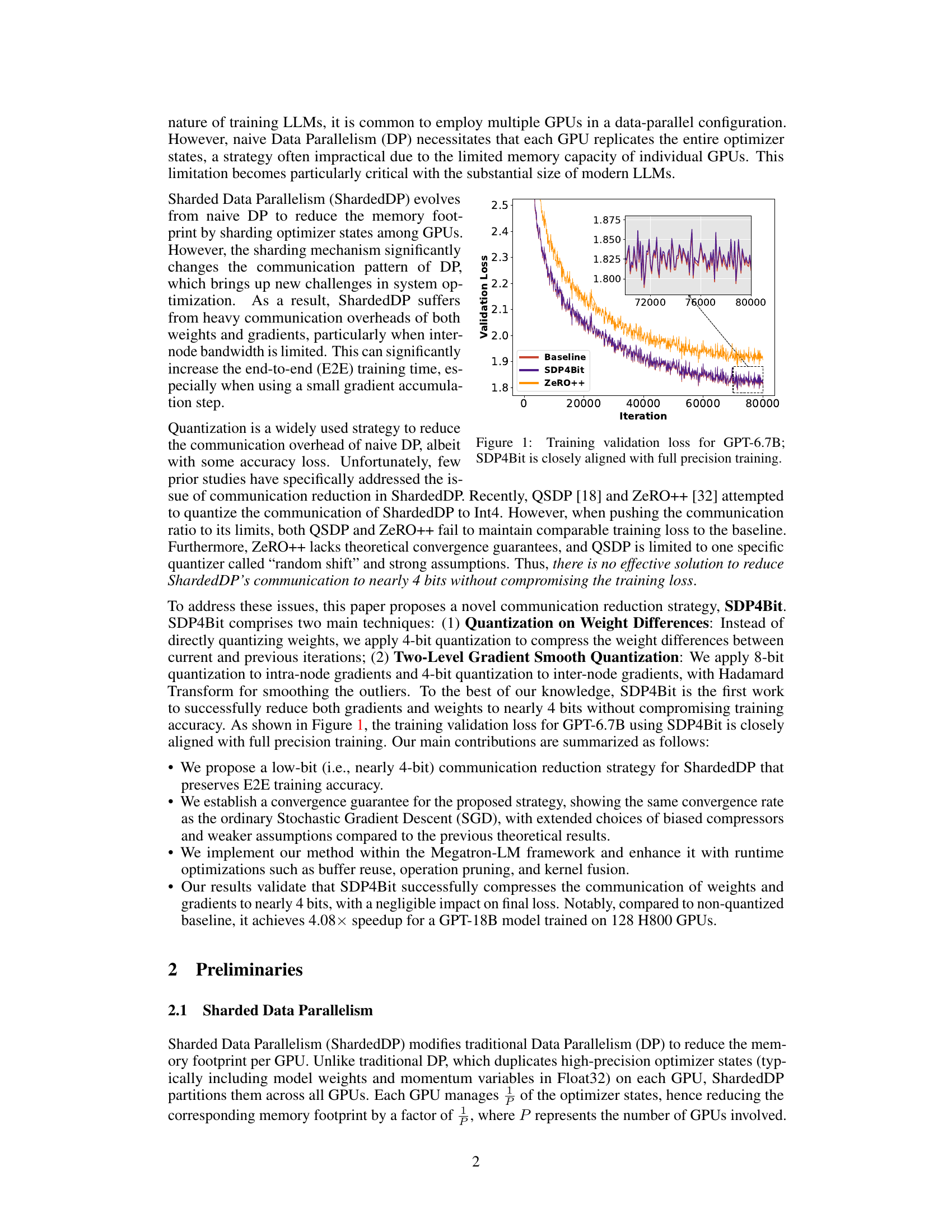
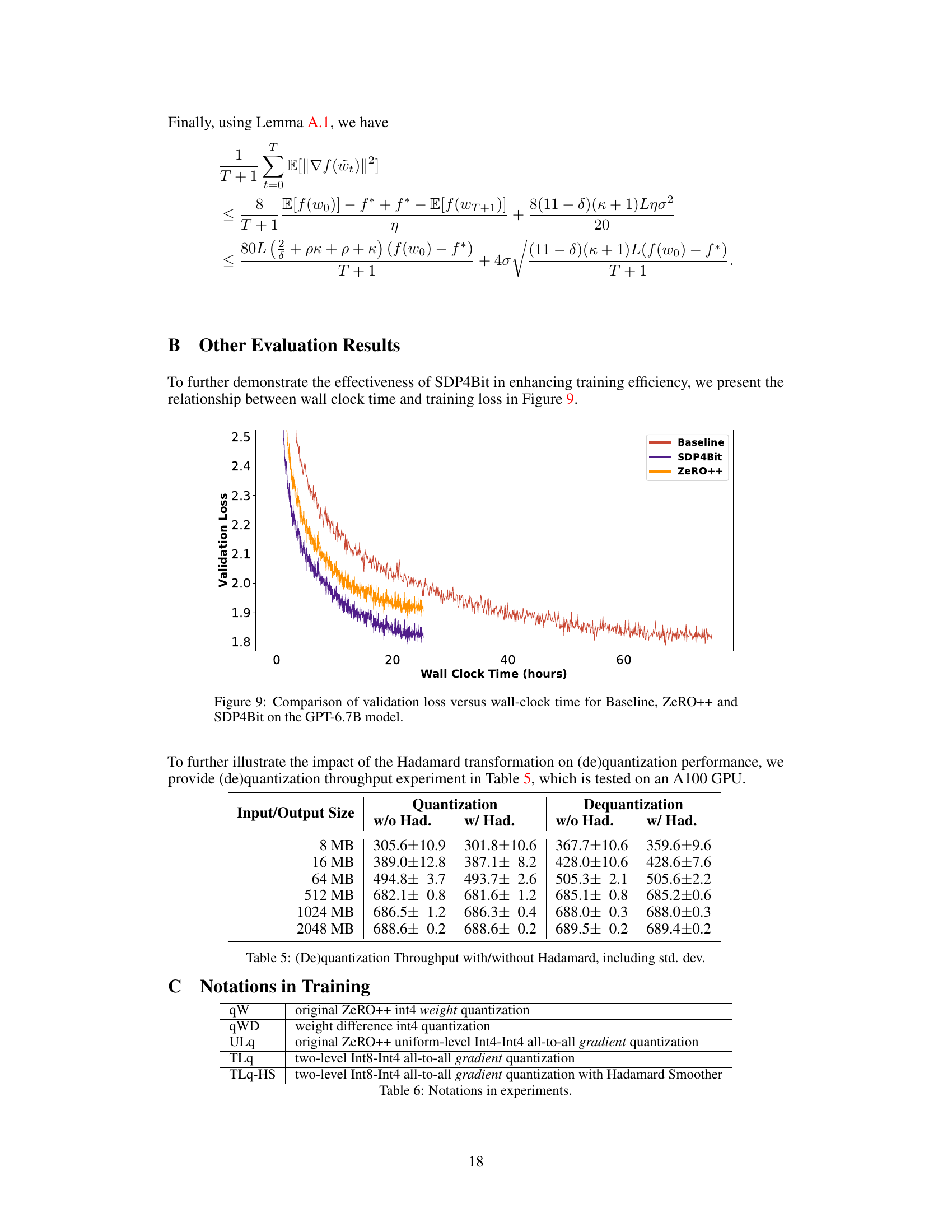
This figure compares the validation loss during training for a GPT-6.7B language model using three different methods: a baseline (full precision), SDP4Bit (the proposed method), and ZeRO++. The plot shows that SDP4Bit closely tracks the baseline’s performance, indicating that the proposed communication quantization technique does not significantly impact training accuracy. In contrast, ZeRO++ exhibits a noticeable deviation from the baseline, suggesting a potential accuracy compromise.

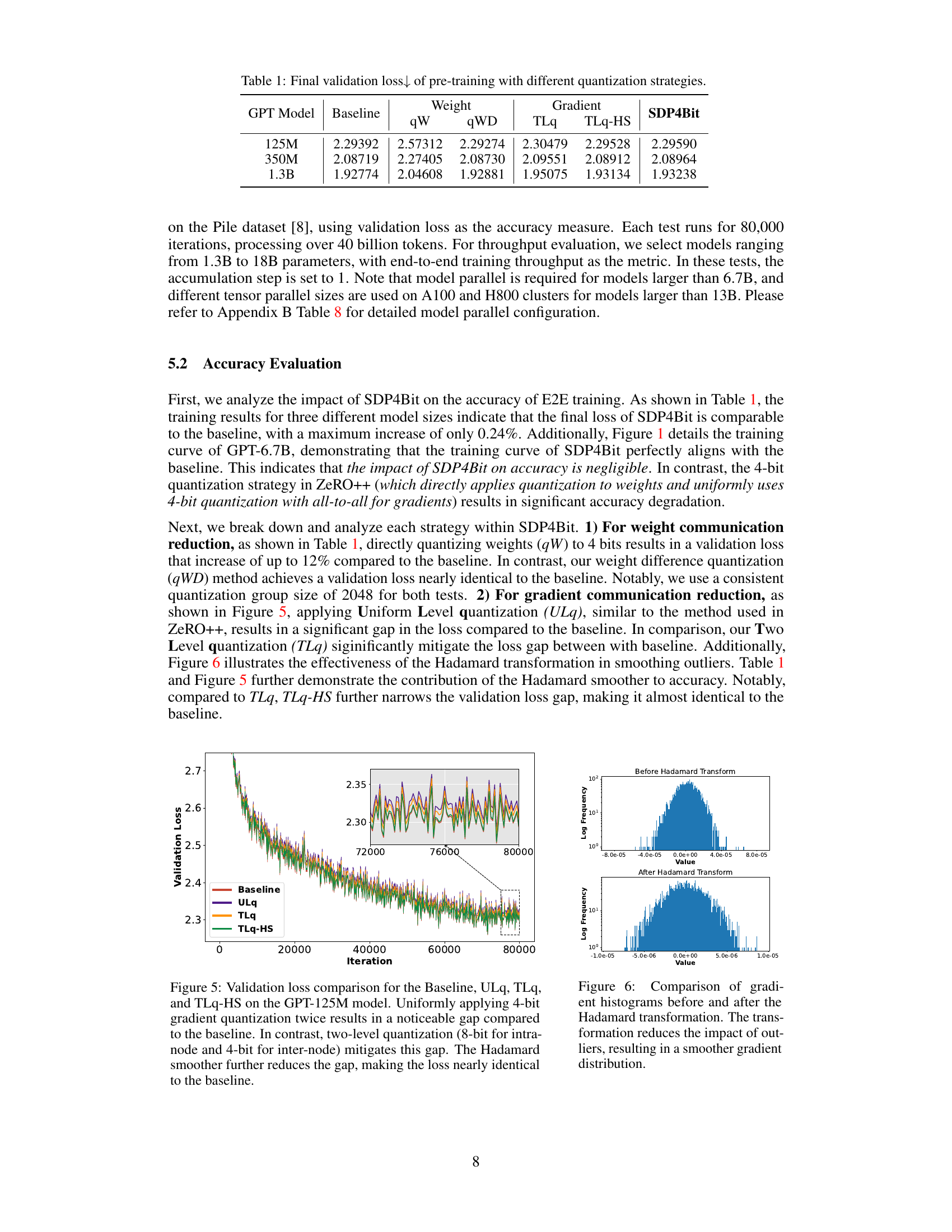
This table presents the final validation loss achieved during the pre-training phase of GPT models with varying sizes (125M, 350M, and 1.3B parameters) using different quantization strategies. The baseline represents the full-precision training without quantization. The strategies compared include: qW (weight quantization), qWD (weight difference quantization), TLq (two-level gradient smooth quantization), and TLq-HS (two-level gradient smooth quantization with Hadamard smoother). The table showcases the impact of different quantization techniques on the final model accuracy, demonstrating that SDP4Bit approaches the accuracy of full-precision training.
In-depth insights#
4-bit Quant. in SDP#
The heading ‘4-bit Quant. in SDP’ suggests a research focus on achieving 4-bit quantization within the context of Sharded Data Parallelism (SDP). This is a significant challenge in large language model (LLM) training, where communication bandwidth between GPUs becomes a major bottleneck. Reducing the precision of communication to 4 bits drastically reduces the data volume transferred, potentially leading to substantial speed improvements. However, it introduces the risk of significant accuracy loss due to the information discarded during quantization. Therefore, the core innovation likely involves novel quantization techniques that minimize information loss despite the extreme compression. This likely includes intelligent methods for selecting which parts of the data to quantize more aggressively, perhaps focusing on less-important information like weight differences, coupled with smoothing techniques to mitigate errors introduced by the low precision. The success of such an approach would represent a major advancement in distributed LLM training, pushing the boundaries of efficient parallelism.
Weight Diff. Quant.#
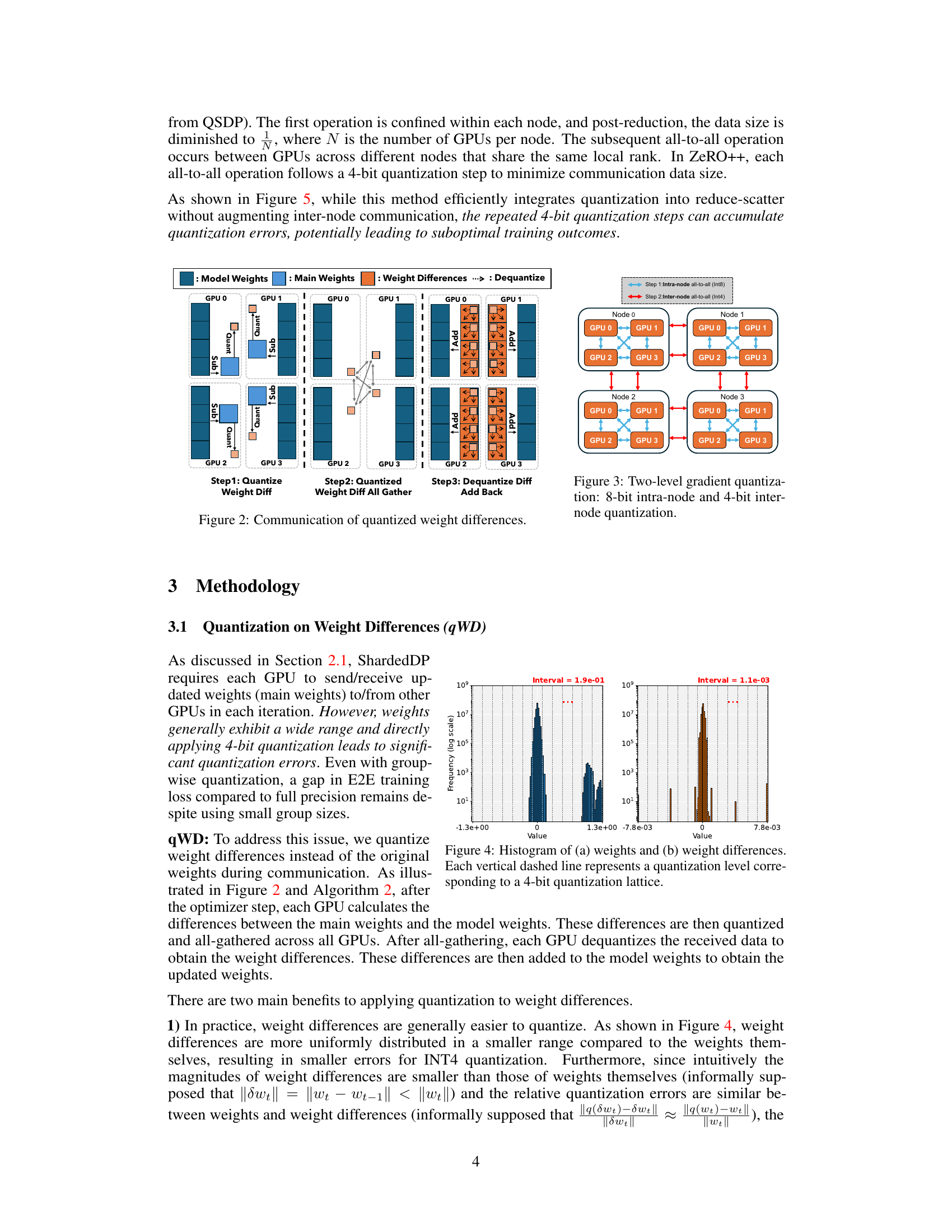
The proposed “Weight Diff. Quant.” technique is a novel approach to address the challenges of communication quantization in sharded data parallelism for large language model (LLM) training. Instead of directly quantizing the model weights, which can lead to significant information loss and accuracy degradation, this method cleverly focuses on quantizing the differences between weights across consecutive training iterations. This subtle shift is critically important, as weight differences often exhibit a smaller dynamic range and are more uniformly distributed compared to the weights themselves. This characteristic makes them significantly easier to quantize effectively using low-bit representations (e.g., 4-bit) with minimal accuracy loss. The theoretical analysis provided in the paper further supports this notion, demonstrating that quantizing weight differences improves convergence and maintains comparable training performance to full-precision methods. In essence, Weight Diff. Quant. represents a smart optimization strategy, balancing compression efficiency with accuracy preservation, crucial for scaling up LLM training across large-scale distributed computing environments.
Gradient Smooth. Quant.#
The concept of ‘Gradient Smooth Quantization’ suggests a method to improve the efficiency of gradient updates in machine learning, especially deep learning, by combining smoothing techniques with quantization. Smoothing likely refers to methods that reduce the impact of outliers or noise in gradients, perhaps by using moving averages or other filtering techniques. This is crucial because noisy gradients can hinder convergence or slow down training. Quantization reduces the precision of gradient values (e.g., from 32-bit floating point to 8-bit integers), thereby reducing the amount of data transmitted during distributed training. This significantly reduces communication overhead, but might introduce quantization errors. The combination of these two aims to mitigate the negative effects of quantization while still achieving significant communication savings. The smoothing step would likely aim to improve the accuracy of the quantized gradients, resulting in less loss of information and hopefully better model performance compared to quantization alone.
System Co-design#
System co-design in the context of large language model (LLM) training, particularly within the framework of sharded data parallelism (ShardedDP), represents a crucial approach to optimizing performance. It involves a holistic approach that considers both algorithmic and system-level optimizations to mitigate the communication bottlenecks inherent in distributed training. Effective system co-design for ShardedDP would incorporate techniques to minimize the computational overhead of compression, such as buffer reuse, operation pruning, and kernel fusion. This is critical because communication compression, while crucial for scalability, can introduce significant latency if not carefully implemented. Furthermore, a successful system co-design strategy would address the interplay between quantization techniques and system architecture; for example, the choice of quantization granularity (bit-width) and the manner in which data is transmitted across nodes must be compatible with the underlying hardware and networking capabilities. The goal is to achieve a balance between communication efficiency and computational accuracy. A well-designed system would dynamically adapt to changing workloads, ensuring optimal utilization of available resources. Finally, system co-design should be evaluated rigorously across diverse hardware and network settings to ensure it is robust and readily adaptable.
Future Works#
Future research directions stemming from this work on SDP4Bit could explore several promising avenues. Extending SDP4Bit’s applicability to various model architectures beyond GPT models would significantly broaden its impact. This includes investigating its effectiveness on vision transformers or other large-scale models with different inherent communication patterns. A thorough analysis of SDP4Bit’s behavior under diverse network conditions, particularly those with varying bandwidth and latency, is crucial for assessing its robustness in real-world deployments. Investigating alternative quantization techniques beyond the two presented here (quantization on weight differences and two-level gradient smooth quantization) may lead to further communication efficiency gains. Exploring potential synergies with other compression methods, like sparsification, warrants attention. Finally, a comprehensive investigation into the trade-off between accuracy and compression ratio, particularly at extremely low bit-widths, should provide valuable insights for optimizing the technique for specific applications.
More visual insights#
More on figures

This figure shows the validation loss curves during the training of a 6.7 billion parameter GPT model. The curves compare the performance of three different training methods: a baseline using full precision, the ZeRO++ method, and the SDP4Bit method proposed in the paper. The graph demonstrates that SDP4Bit achieves a validation loss curve very close to the full precision baseline, indicating comparable accuracy. The ZeRO++ method shows a higher validation loss.
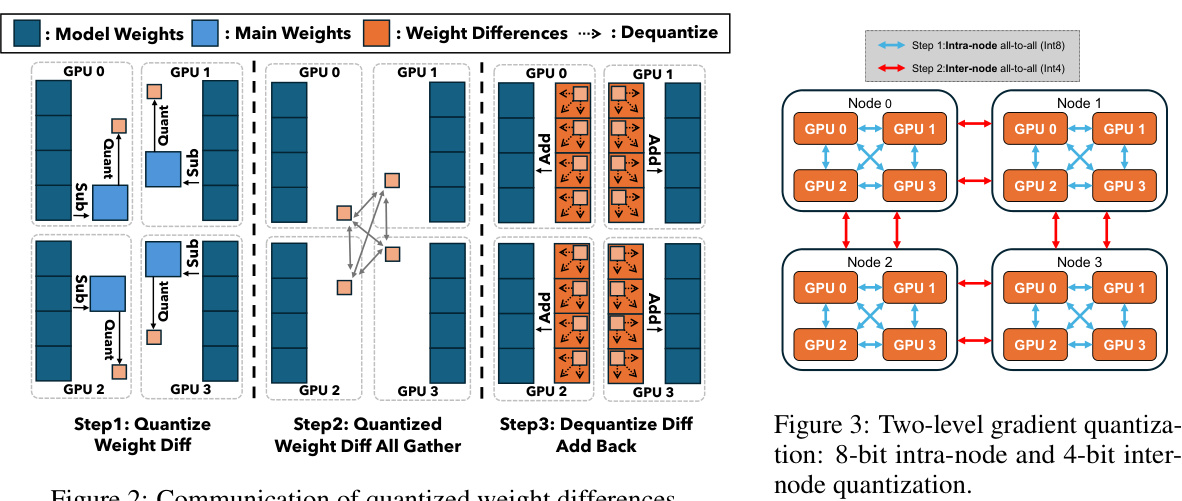
This figure illustrates the two-level gradient quantization technique used in SDP4Bit. It shows how gradients are first quantized to 8 bits within each node (intra-node) using an all-to-all communication. Then, the reduced data is further quantized to 4 bits for communication between nodes (inter-node) via another all-to-all operation. This two-level approach balances accuracy and communication efficiency. The figure uses a visual representation to show the process across multiple nodes and GPUs.

This figure shows two histograms. The left one displays the distribution of weights, illustrating a wide range of values. The right one shows the distribution of weight differences (between consecutive iterations), demonstrating a narrower and more uniform distribution centered around zero. The vertical dashed lines in both histograms represent the quantization levels for a 4-bit quantization scheme. This visualization supports the paper’s claim that quantizing weight differences leads to smaller quantization errors and better performance compared to directly quantizing the weights.
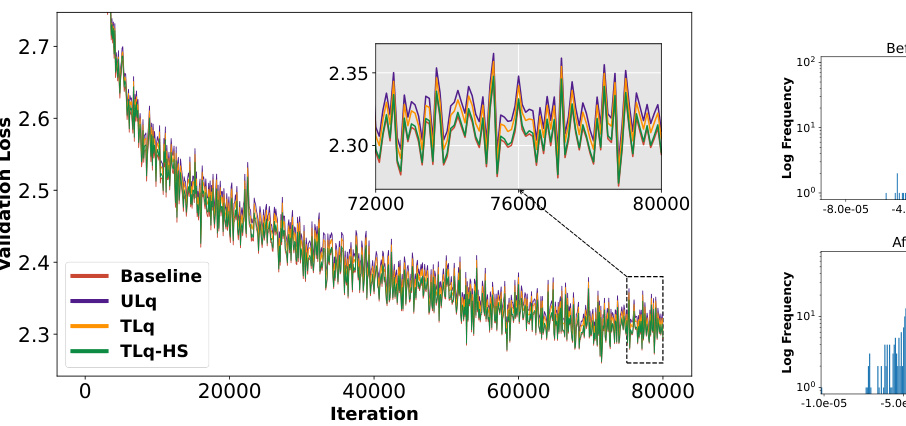
This figure compares the validation loss curves of four different methods for training a GPT-125M model: Baseline (full precision), ULq (uniform level quantization), TLq (two-level quantization), and TLq-HS (two-level quantization with Hadamard smoother). It demonstrates that directly applying 4-bit quantization to gradients twice (ULq) results in significantly higher validation loss compared to the baseline. The two-level approach (TLq) reduces this gap by quantizing intra-node gradients to 8 bits and inter-node gradients to 4 bits. Finally, the addition of the Hadamard smoother (TLq-HS) further improves the result, achieving validation loss almost identical to the baseline.
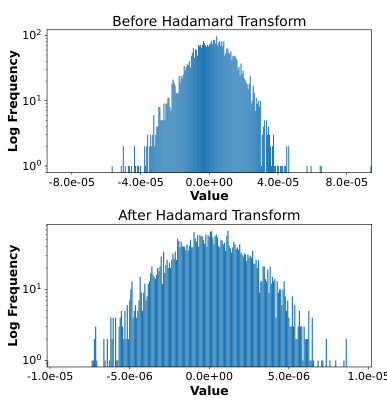
This figure shows two histograms visualizing the distribution of gradients before and after applying the Hadamard transform. The histogram on top represents the gradient distribution before transformation, exhibiting a sharp peak and heavier tails, indicating the presence of outliers. The bottom histogram shows a much smoother, more Gaussian-like distribution after the Hadamard transform, illustrating how this technique successfully mitigates the effect of outliers by spreading their influence across other gradient components. This results in a more stable and less noisy gradient signal that is potentially less susceptible to quantization errors.
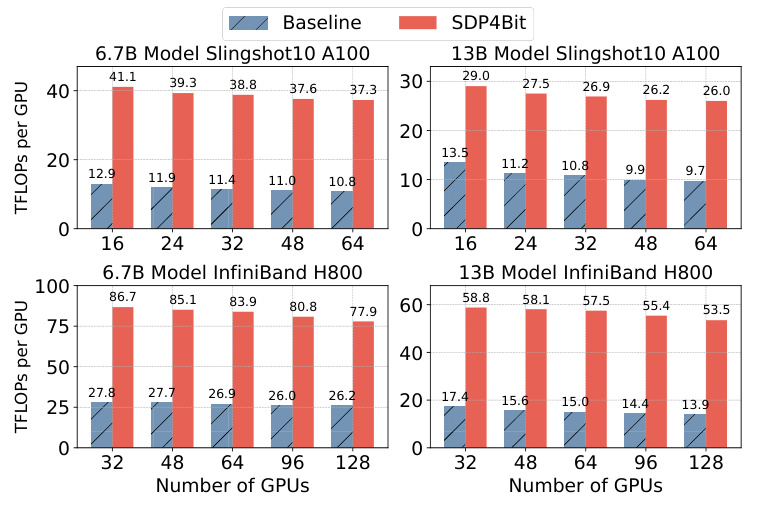
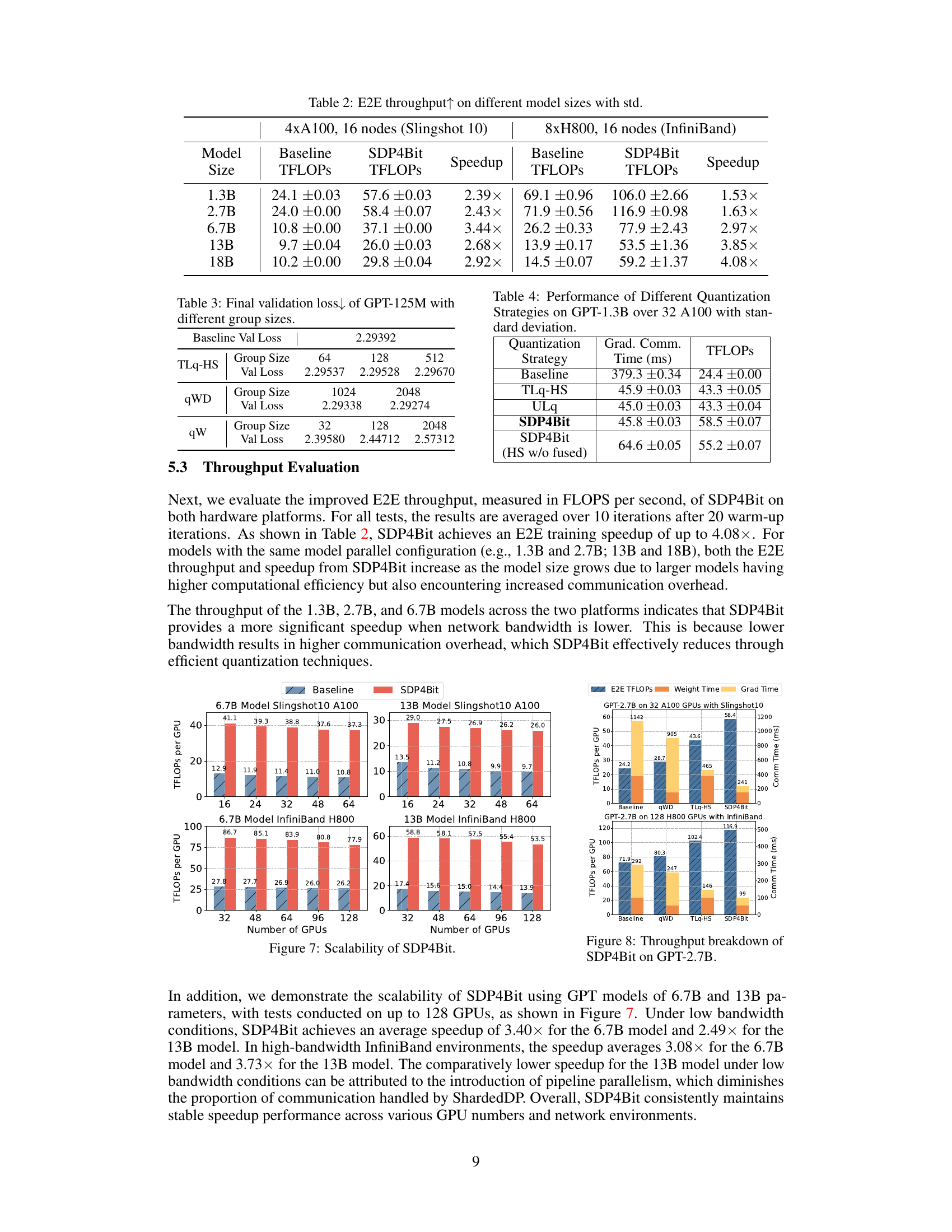
This figure demonstrates the scalability of SDP4Bit using GPT models of 6.7B and 13B parameters, with tests conducted on up to 128 GPUs. The left two plots show results on a cluster with slower inter-node bandwidth (Slingshot10), while the right two use a high-bandwidth InfiniBand network. The bars show the achieved throughput (TFLOPS per GPU) for baseline Megatron-LM and SDP4Bit at varying GPU counts. SDP4Bit demonstrates consistent speedups across different GPU counts and network conditions.
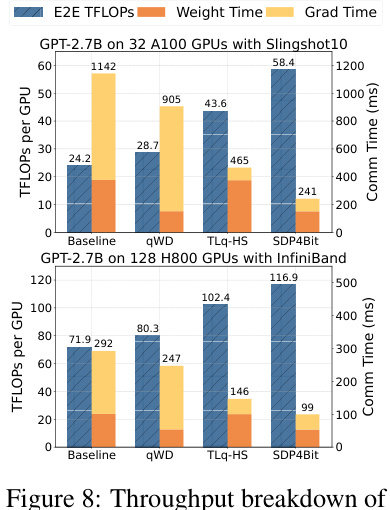
This figure shows a throughput breakdown of the SDP4Bit model on two different hardware platforms: 32 A100 GPUs with Slingshot10 network and 128 H800 GPUs with InfiniBand network. For each platform, it compares the baseline performance with three variations of the SDP4Bit algorithm: - qWD (Quantization on Weight Differences): shows the impact of only quantizing weight differences on throughput. - TLq-HS (Two-Level Gradient Smooth Quantization with Hadamard Smoother): shows the effect of using the two-level gradient quantization and Hadamard smoother. - SDP4Bit (the full algorithm): combines both qWD and TLq-HS. The figure displays the E2E throughput in TFLOPS per GPU and the communication time spent on weights and gradients in milliseconds (ms). This allows visualization of how each component contributes to the overall throughput improvement of SDP4Bit across different hardware and network conditions.

This figure compares the training progress (validation loss) over time (wall-clock hours) for three different methods: the Baseline (full-precision training), SDP4Bit (the proposed method), and ZeRO++. It demonstrates that SDP4Bit achieves comparable accuracy to the baseline while being significantly faster than ZeRO++. The graph shows the validation loss decreasing over time for all three methods, with SDP4Bit closely tracking the baseline’s performance.
More on tables

This table presents the final validation loss achieved during the pre-training phase of various GPT models, comparing different quantization strategies. The baseline represents full precision training, while ‘qW’ uses 4-bit quantization on weights, ‘qWD’ uses 4-bit quantization on weight differences, ‘TLq’ employs two-level gradient quantization, and ‘TLq-HS’ adds a Hadamard smoother to TLq. The table demonstrates the impact of each strategy on the model’s final accuracy, highlighting the effectiveness of SDP4Bit in achieving near-baseline accuracy with significant compression.
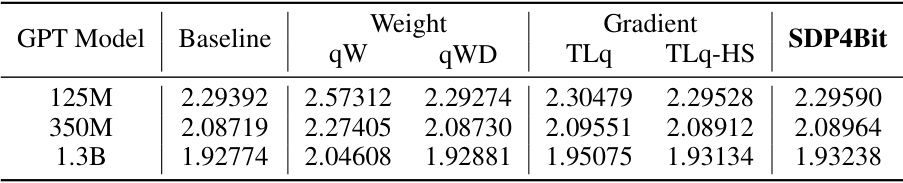
This table presents the final validation loss achieved during the pre-training phase of GPT models with varying sizes (125M, 350M, and 1.3B parameters). It compares the performance of different quantization strategies, including the baseline (no quantization), weight quantization (qW and qWD), and gradient quantization (TLq and TLq-HS), against the proposed SDP4Bit method. Lower validation loss indicates better model performance.
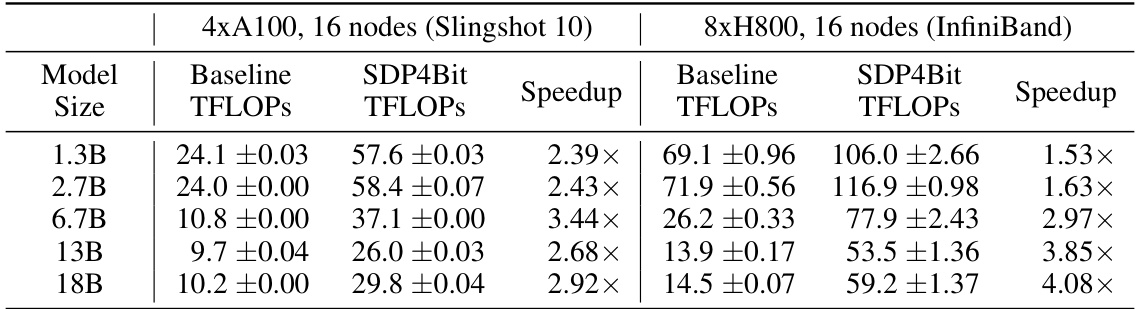
This table shows the end-to-end (E2E) throughput, measured in TFLOPS (trillion floating-point operations per second), for different GPT model sizes (1.3B, 2.7B, 6.7B, 13B, and 18B parameters) using two different hardware setups. The first setup uses 16 nodes, each with 4xA100 GPUs and interconnected with a Slingshot 10 network. The second setup uses 16 nodes with 8xH800 GPUs and InfiniBand interconnect. For each model size and hardware setup, the table presents the baseline throughput (without SDP4Bit), the throughput achieved using the SDP4Bit technique, and the speedup factor (SDP4Bit throughput divided by baseline throughput). The speedup factor indicates the performance improvement obtained by using the SDP4Bit method.
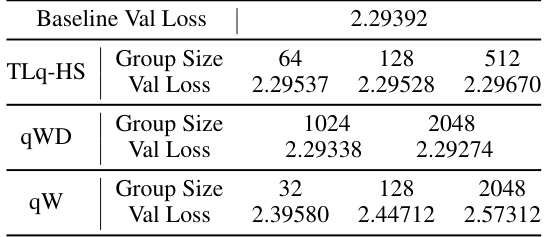
This table shows the final validation loss for the GPT-125M model using different group sizes for three different quantization methods: TLq-HS, qWD, and qW. It demonstrates the effect of varying the group size on the accuracy of each quantization technique, showing how the choice of group size impacts the final validation loss compared to the baseline.

This table compares the performance of different quantization strategies on a GPT-1.3B model trained on 32 A100 GPUs. It shows the gradient communication time (in milliseconds) and the resulting throughput in TFLOPS for four strategies: Baseline (no quantization), TLq-HS (Two-Level quantization with Hadamard Smoother), ULq (Uniform Level quantization), and SDP4Bit. The table also includes a comparison for SDP4Bit without kernel fusion of Hadamard transform for reference. This comparison demonstrates the efficiency gains achieved by SDP4Bit in reducing communication overhead while improving throughput.

This table presents the throughput results of the quantization and dequantization processes with and without the Hadamard transform. The measurements are given in terms of the throughput (in MB/s) for different input/output sizes (8 MB to 2048 MB). The standard deviations are included to show the variability of the measurements. The data suggests that the Hadamard transform has minimal impact on the throughput of (de)quantization process.

This table presents the final validation loss achieved during the pre-training phase of GPT models with varying sizes (125M, 350M, and 1.3B parameters). It compares the performance of different quantization strategies: the baseline (no quantization), quantization on weights (qW), quantization on weight differences (qWD), two-level gradient smooth quantization (TLq), and two-level gradient smooth quantization with Hadamard Smoother (TLq-HS). The results demonstrate the effectiveness of SDP4bit’s approach in maintaining accuracy while significantly reducing communication overhead.

This table presents the final validation loss achieved during the pre-training of GPT models with various sizes (125M, 350M, and 1.3B parameters) using different quantization strategies. The strategies compared include the baseline (no quantization), quantization on weights (qW), quantization on weight differences (qWD), two-level gradient smooth quantization (TLq), and two-level gradient smooth quantization with Hadamard smoother (TLq-HS). This allows for a comparison of the impact of different quantization approaches on the final model accuracy, measured by validation loss.
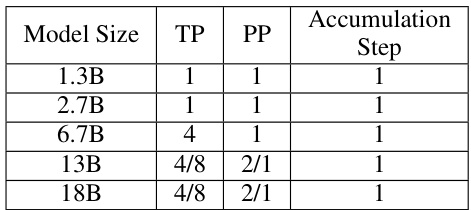
This table shows the parallel configuration used for the throughput tests in the paper. It specifies the tensor parallel (TP), pipeline parallel (PP) size, and accumulation step for different GPT model sizes (1.3B, 2.7B, 6.7B, 13B, and 18B). These configurations were chosen to maximize throughput on the hardware platforms used in the experiments. The variation in TP and PP values reflects different strategies for maximizing throughput with varying model sizes and hardware limitations.

This table shows the final validation loss achieved during the pre-training of GPT models with different sizes (125M, 350M, and 1.3B parameters) using various quantization strategies. The strategies include a baseline (no quantization), weight quantization (qW), weight difference quantization (qWD), two-level gradient quantization (TLq), and two-level gradient quantization with Hadamard smoother (TLq-HS). The table highlights the impact of different quantization methods on the final model accuracy, comparing them to the baseline (full precision training).
Full paper#