↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Offline reinforcement learning faces challenges due to limited data and the risk of policies generating out-of-distribution actions, leading to poor performance and unreliable value estimations. Model-based methods attempt to address this by learning environmental dynamics to guide policy search, but errors in model estimation and value overestimation remain significant hurdles.
C-LAP innovatively tackles these issues by learning a generative model of joint state-action distributions. By casting policy learning as a constrained objective, C-LAP ensures that generated actions always stay within the distribution’s support. This eliminates the need for additional uncertainty penalties, reducing the number of training steps. Empirical evaluations on standard benchmarks show C-LAP’s competitiveness with state-of-the-art methods, demonstrating superior performance with visual observations, thereby offering a more robust and efficient offline RL approach.
Key Takeaways#
Why does it matter?#
This paper is important because it tackles the persistent problem of value overestimation in model-based offline reinforcement learning, a critical challenge hindering the progress of this field. The proposed C-LAP method offers a novel solution by jointly modeling state-action distributions, implicitly constraining the policy to avoid out-of-distribution actions and thus improving the reliability and efficiency of offline RL. This work opens avenues for further exploration in efficient and robust offline RL algorithms, pushing the boundaries of applicability in real-world scenarios where data collection is expensive or unsafe.
Visual Insights#

This figure illustrates the three main steps of the Constrained Latent Action Policies (C-LAP) method. Panel (a) shows the offline training phase where the model learns to encode observations and actions into latent variables, and then decode these to predict rewards. Panel (b) depicts the policy training phase. The policy is trained in the latent action space, subject to constraints that keep generated actions within the observed data distribution. Panel (c) shows how the trained policy is used in the real world, using the learned decoder to generate actions from latent representations.

This table presents the results of the C-LAP model and other baselines on the D4RL benchmark. It shows the average normalized returns and standard deviations obtained by each method across different locomotion and antmaze environments. Each environment is tested with various datasets representing different levels of expertise, from medium replay to expert. The results demonstrate the relative performance of C-LAP compared to other state-of-the-art offline reinforcement learning methods.
In-depth insights#
Latent Action Models#
Latent action models represent a powerful paradigm shift in reinforcement learning, addressing limitations of traditional methods. By introducing a latent space for actions, these models decouple the observed actions from the policy’s decision-making process. This allows for more flexible and efficient exploration of the action space, particularly beneficial in complex environments with high-dimensional or continuous actions. The key advantage lies in the ability to learn a compact representation of actions, capturing underlying structure and reducing the dimensionality of the problem. This not only improves learning efficiency but also enhances generalization capabilities, leading to better performance in unseen scenarios. Furthermore, the latent space enables the imposition of constraints, facilitating safer and more controlled policy optimization, especially valuable in offline reinforcement learning where out-of-distribution actions can be detrimental. However, the success of latent action models relies heavily on effective encoding and decoding of actions, requiring carefully designed architectures capable of capturing the essential features while avoiding information loss. The design and training of these models present computational challenges, demanding significant resources and careful tuning of hyperparameters. The interpretability of the latent space also remains an open question, making it crucial to develop methods for assessing and understanding the learned representation.
Offline RL#
Offline reinforcement learning (RL) presents a unique challenge in that it seeks to learn optimal policies from a static dataset collected beforehand, without the ability to actively interact with the environment. This differs significantly from online RL, where agents learn through trial-and-error. The key difficulty lies in the potential for distributional shift, where the data distribution used for training may differ significantly from the distribution experienced by the learned policy during deployment, leading to poor generalization and unpredictable behavior. Model-based methods, which learn an environment model from data, offer a potential solution, but are susceptible to errors in the model and value overestimation. Model-free approaches, on the other hand, directly learn a policy from the data, often addressing distributional shift through techniques like behavioral cloning or conservative Q-learning. The choice between these approaches and the specific techniques used heavily impact the success of offline RL in various applications.
C-LAP Algorithm#
The Constrained Latent Action Policies (C-LAP) algorithm is a novel approach to offline model-based reinforcement learning that tackles the critical problem of value overestimation. C-LAP cleverly addresses this by jointly modeling the state and action distributions, rather than relying on traditional conditional dynamics modeling. This joint modeling establishes an implicit constraint, ensuring generated actions remain within the support of the observed data distribution. The algorithm utilizes a recurrent latent action state-space model which allows it to learn a policy within a constrained latent action space, significantly reducing the number of gradient steps needed during training. Instead of using uncertainty penalties, C-LAP leverages the generative capabilities of the model to implicitly confine the actions, making it more efficient and robust. This innovative technique, coupled with an actor-critic approach, results in a policy that generalizes well, especially demonstrating superior performance on datasets with high-dimensional visual observations. The success of C-LAP hinges on its ability to learn a generative model of states and actions, which enables implicit action constraints and enhances policy learning. By jointly learning actions and states, C-LAP effectively avoids the pitfalls of explicit regularization techniques, proving its efficacy and efficiency in offline model-based RL.
Value Overestimation#
Value overestimation is a critical problem in offline reinforcement learning (RL), where an agent learns a policy from a fixed dataset without interacting with the environment. Because the dataset may not comprehensively cover all possible states and actions, the learned model might overestimate the value of actions that lead to out-of-distribution states. This overestimation arises from the model’s inability to generalize accurately beyond the training data, leading to poor performance and unstable training. Model-based methods, which learn a model of the environment dynamics, are particularly susceptible as inaccurate models can easily produce inflated value estimates. Techniques to mitigate overestimation often involve adding penalties to the Bellman update or using ensemble methods to better capture uncertainty. However, such methods can also introduce biases or increase computational cost. This paper proposes to mitigate overestimation by learning a model that explicitly constrains actions, leading to better generalization and avoiding the need for the additional uncertainty penalties used by many prior methods.
Visual Observation#
The use of visual observations in reinforcement learning presents unique challenges and opportunities. Visual data is high-dimensional and complex, requiring specialized architectures like convolutional neural networks for effective processing. However, the richness of visual information can significantly improve the agent’s understanding of the environment. This is especially true in scenarios where low-dimensional state representations might be insufficient or misleading. Model-based methods are particularly well-suited to handling visual inputs because their ability to learn a generative model of the environment allows them to predict the effects of actions in unseen situations. In offline settings, the ability to generalize from limited visual data is crucial for avoiding the pitfalls of out-of-distribution samples. Effective handling of visual data can also improve robustness against noise and variations in lighting or viewpoint. Methods designed for visual data often incorporate techniques for reducing dimensionality or dealing with uncertainty, which is crucial for ensuring effective learning and decision making.
More visual insights#
More on figures

This figure illustrates the recurrent latent action state-space model used in the Constrained Latent Action Policies (C-LAP) method. It shows how observations (Ot), actions (at), latent states (st), and latent actions (ut) are interconnected through stochastic and deterministic processes. The solid lines represent the generative process (model’s forward pass), while the dashed lines represent the inference process (model’s backward pass). Circles denote stochastic variables, and rectangles represent deterministic variables. The model learns a joint distribution of states and actions, rather than a conditional dynamics model p(s|a), which is a key aspect of the C-LAP approach. The figure visually summarizes the core structure of the generative model which is detailed mathematically in the paper.
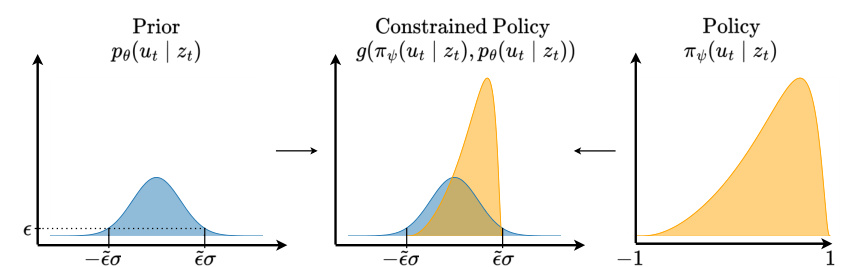
This figure illustrates how the policy is constrained to the data distribution by using a linear transformation. The prior distribution is shown in light blue. The policy distribution in orange is constrained to be within the range defined by the prior, ensuring the generated actions are within the bounds of the training data. The constraint is implemented through a linear transformation of the latent action prior and the bounded policy, as shown in the middle panel. This ensures that the policy is flexible but still respects the implicit constraint imposed by the data distribution. Finally, the fully trained policy distribution is shown in the right-most panel.

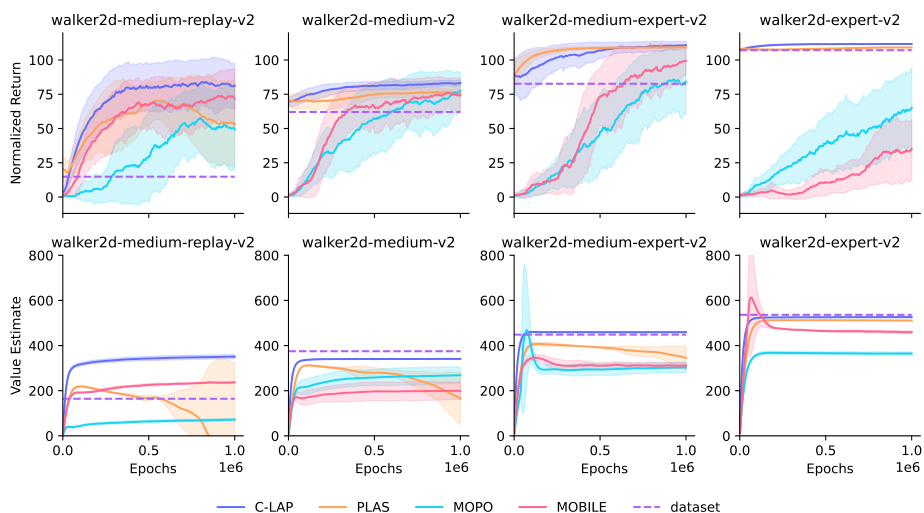
This figure shows the training curves for four different offline reinforcement learning algorithms (C-LAP, MOPO, MOBILE, PLAS) across various D4RL benchmark locomotion tasks (halfcheetah, walker2d, hopper) and navigation tasks (antmaze). Each task has four datasets representing varying levels of data quality (medium-replay, medium, medium-expert, expert). The y-axis represents the normalized average return, and the x-axis represents the number of gradient steps taken during training. Error bars show the standard deviation across four different training runs. The figure demonstrates the performance comparison of C-LAP against state-of-the-art methods on low-dimensional feature observation datasets.

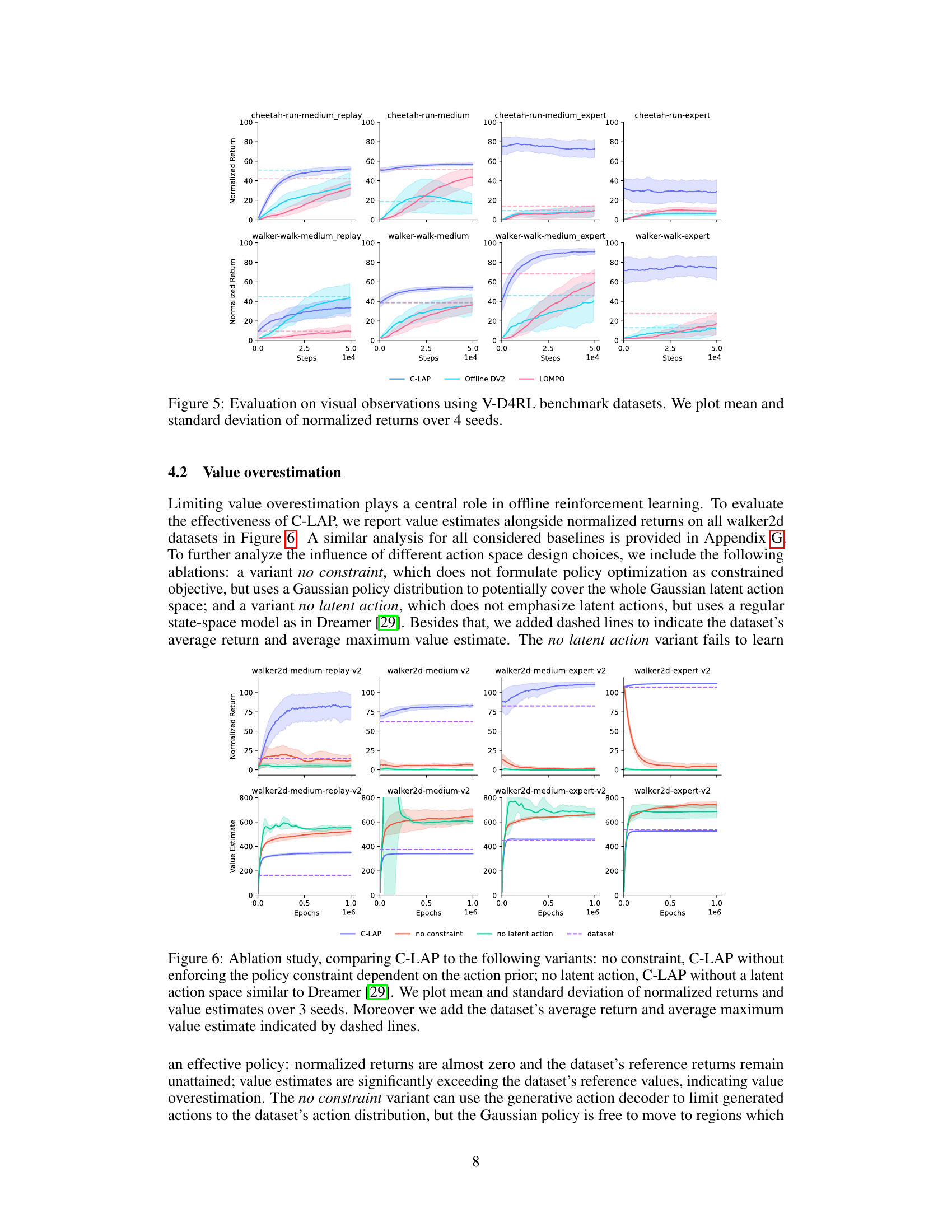
This figure shows the performance of C-LAP, Offline DV2, and LOMPO on four different V-D4RL benchmark datasets with visual observations. Each dataset represents a different level of data complexity (replay, medium, medium-expert, expert). The plot displays the mean and standard deviation of normalized returns over four separate runs (seeds), demonstrating the performance and variability of each method across different trials. This helps to illustrate how the methods perform on data with varying levels of complexity.

This figure presents an ablation study comparing the performance of C-LAP against variations where the policy constraint is removed, and where a latent action space is not used, similar to Dreamer. The results are shown in terms of normalized returns and value estimates, along with dataset average return and maximum value estimate for comparison. The study helps analyze the impact of the key components of the C-LAP model on its performance in offline reinforcement learning.

This figure shows the sensitivity analysis of the support constraint parameter (epsilon) on the performance of C-LAP across four walker2d datasets from the D4RL benchmark. The x-axis represents the epochs during training, and the y-axis represents the normalized returns. Different lines show the result for various values of epsilon, from 0.5 to 10.0, illustrating how this hyperparameter impacts the learning process and the model’s final performance. The shaded areas represent standard deviations over 4 seeds.

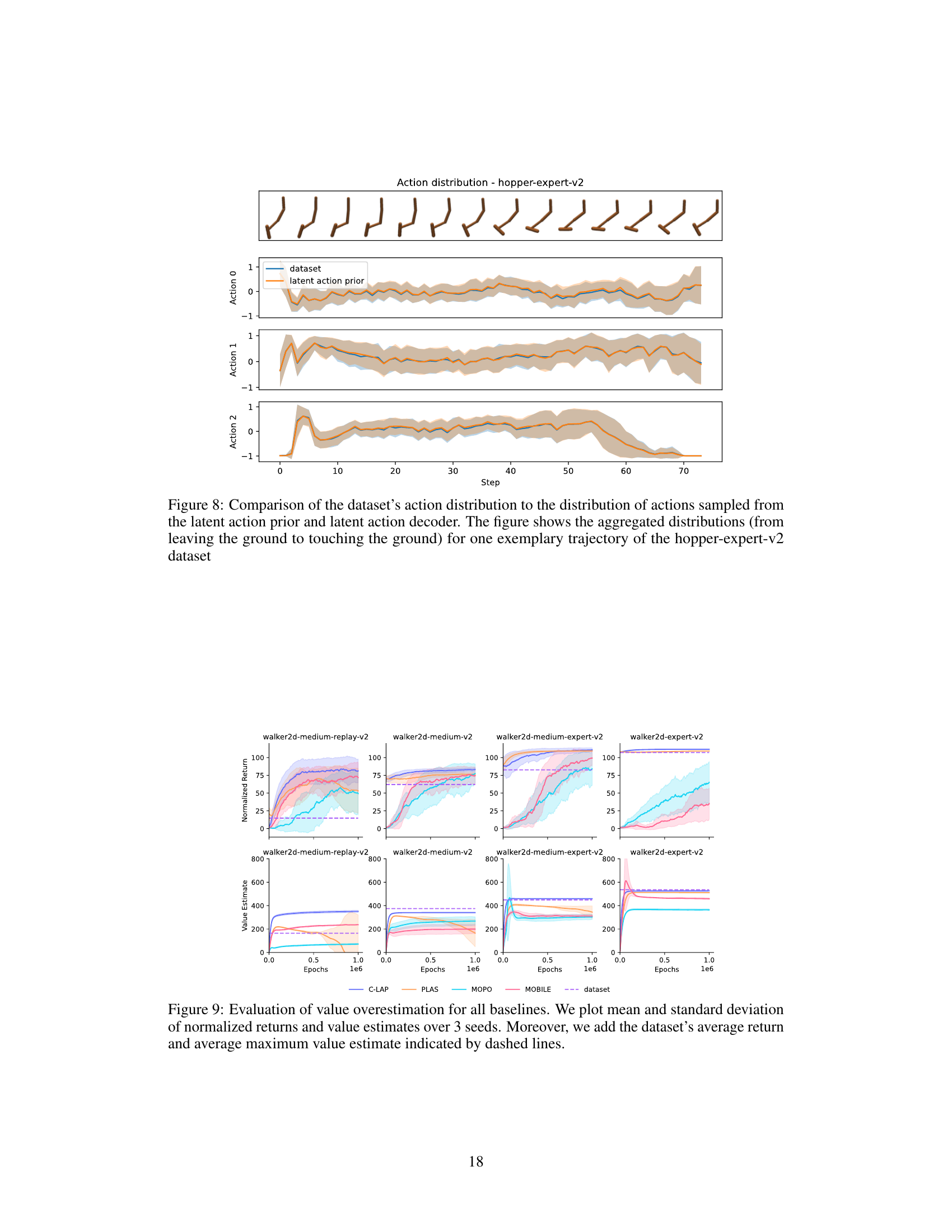
This figure compares the distribution of actions from the dataset and the distribution of actions generated by the model’s latent action prior and decoder. The comparison is done for one trajectory from the hopper-expert-v2 dataset and shows that the model-generated actions are close to the dataset’s actions distribution.
This figure shows an ablation study comparing the performance of C-LAP with three variants: one without the constraint on the policy (allowing it to explore outside the data distribution), one without latent actions (using a simpler state-space model), and the original C-LAP model. The plots show both the normalized returns and the value estimates over epochs for four different datasets (walker2d-medium-replay-v2, walker2d-medium-v2, walker2d-medium-expert-v2, and walker2d-expert-v2). Dashed lines represent the average return and the average maximum value estimate from the datasets, providing context for evaluating the performance of each model variant.
More on tables

This table lists the hyperparameters used for the MOPO and MOBILE algorithms when run on the expert datasets of the D4RL benchmark. It shows the ranges explored for penalty coefficient, rollout steps, and dataset ratio, and then provides the specific values selected for each of the three locomotion environments (halfcheetah, walker2d, and hopper).
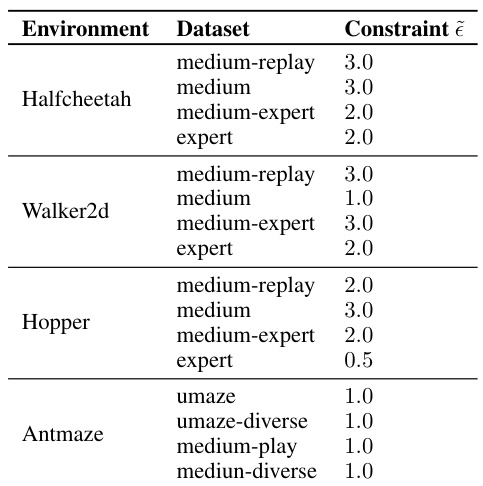
This table shows the hyperparameter values used for the C-LAP model on different datasets within the D4RL benchmark. Specifically, it lists the constraint parameter (ẽ) used for each environment and dataset combination. The constraint parameter influences how closely the generated actions stay within the support of the dataset’s action distribution.

This table shows the hyperparameter (\tilde{\epsilon}) used in the C-LAP algorithm for different environments and datasets in the V-D4RL benchmark. The constraint (\tilde{\epsilon}) is used to limit the generated actions within the support of the dataset’s action distribution. Different values for (\tilde{\epsilon}) are used based on the environment and the dataset.

This table lists the hyperparameters used in the Constrained Latent Action Policies (C-LAP) method. It is divided into two sections: Model and Agent. The Model section specifies details about the architecture of the generative model including the sizes of latent spaces, the types of layers used (MLP or CNN), and the distributions used for outputs. The Agent section provides parameters related to the actor-critic algorithm used for policy training, such as hidden unit sizes, layer numbers, learning rates, and activation functions. Note that different hyperparameter values were used for experiments with low-dimensional features and for experiments with visual observations.
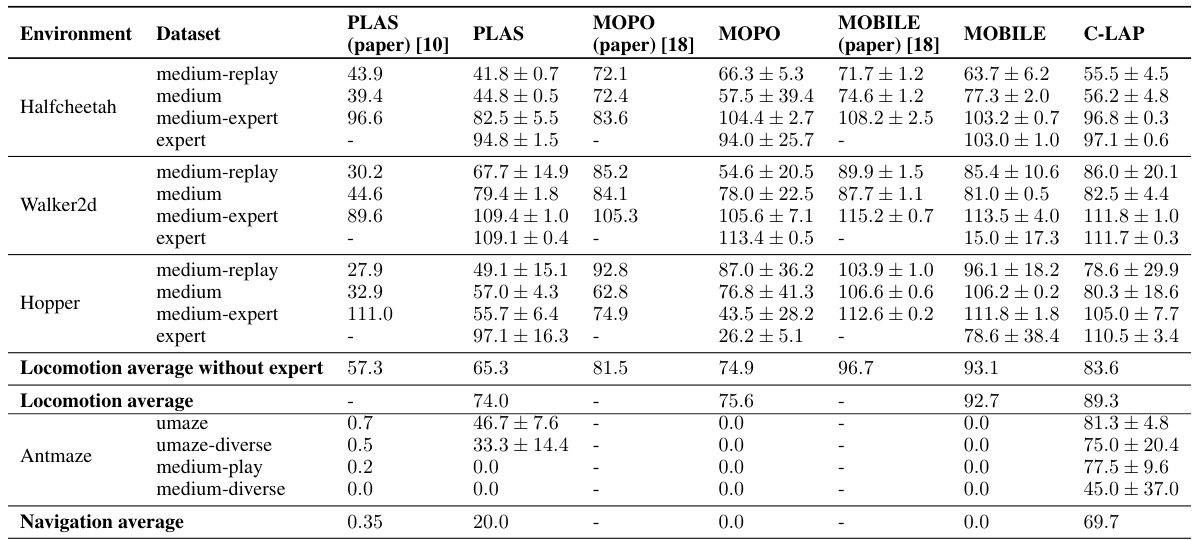
This table presents the results of the experiments conducted on the D4RL benchmark. It shows the performance of different offline reinforcement learning algorithms (PLAS, MOPO, MOBILE, C-LAP) across various locomotion and antmaze environments. For each environment and dataset, the table lists the mean normalized returns achieved by each algorithm, along with their standard deviations, indicating the variability in performance across different runs. The results highlight the relative performance of the proposed C-LAP method compared to existing state-of-the-art methods.
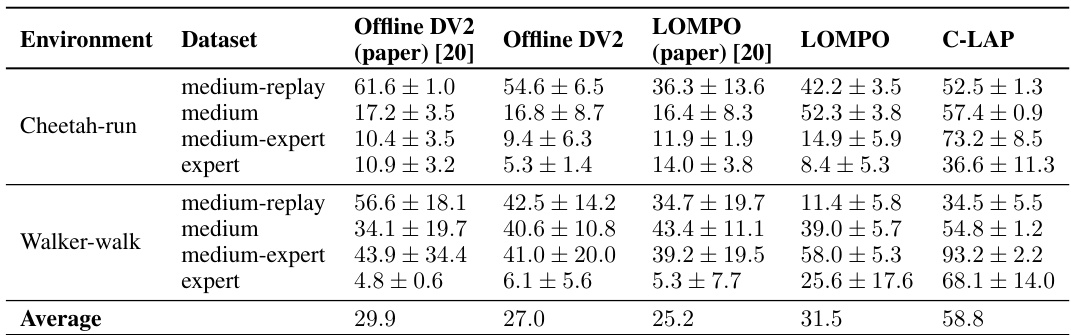
This table presents the results of the proposed C-LAP method and other baselines on the V-D4RL benchmark. The benchmark includes datasets with visual observations. The table shows the average normalized returns and standard deviations across multiple runs for each method on different datasets. The results demonstrate the performance of C-LAP compared to state-of-the-art methods.
Full paper#