Faster Accelerated First-order Methods for Convex Optimization with Strongly Convex Function Constraints

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in optimization and machine learning because it significantly improves the speed and efficiency of solving convex optimization problems with strong convex constraints. The proposed algorithms have order-optimal complexity, exceeding existing methods. Its application to sparse optimization, particularly personalized PageRank, shows strong practical relevance, opening new avenues for solving large-scale problems and identifying optimal sparsity patterns.

Visual Insights

#

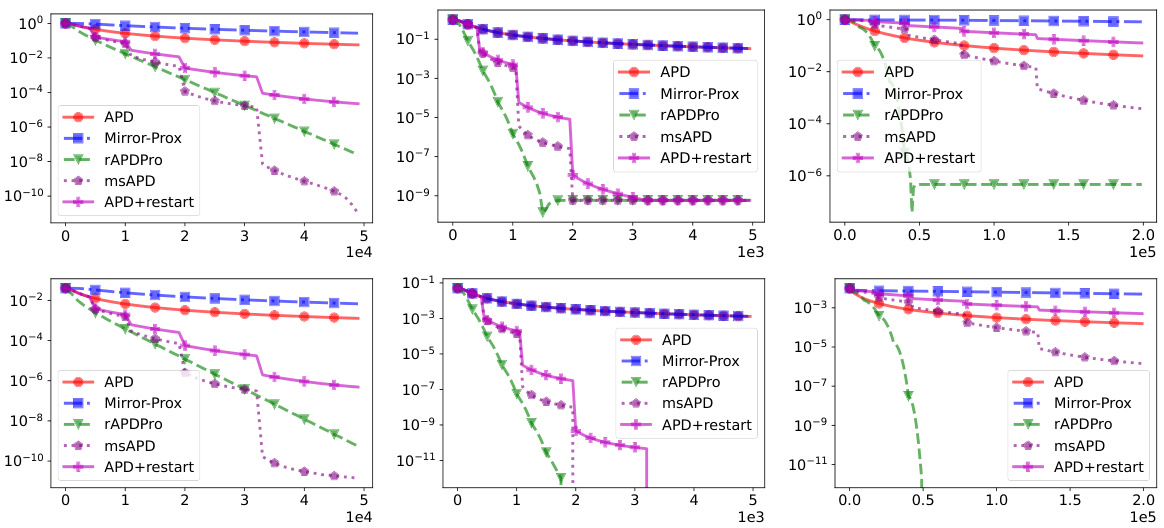
This figure displays the convergence performance and feasibility violation of different algorithms for solving the sparse Personalized PageRank problem on three datasets: bio-CE-HT, bio-CE-LC, and econ-beaflw. The top row shows the convergence to the optimum in terms of the relative function value gap, while the bottom row shows the feasibility violation. The algorithms compared include APD, APD+restart, msAPD, Mirror-Prox, and the proposed rAPDPro. The plots show that rAPDPro and msAPD converge significantly faster and to a higher precision than the other algorithms.

This table lists the six datasets used in the paper’s experiments. For each dataset, it provides the number of nodes (n), the number of edges, and the parameters (b) and (\alpha) used in the personalized PageRank problem. The datasets vary in size and origin, encompassing various domains like biology and economics.

In-depth insights

#

Strong Convexity

#

The concept of strong convexity plays a crucial role in the research paper, significantly impacting the performance and convergence rate of optimization algorithms. Strong convexity of the constraint function enables faster convergence compared to the standard convex case. The authors introduce novel techniques to leverage this strong convexity, achieving an improved complexity bound for minimizing a convex function subject to strongly convex constraints. Progressive estimation of the strong convexity of the Lagrangian function is a key aspect of their approach, leading to more aggressive step sizes and faster convergence. This improved complexity matches the theoretical lower bound, indicating order-optimality. The impact of strong convexity is further explored in the context of sparsity-inducing optimization, demonstrating its effectiveness in identifying the optimal solution’s sparsity pattern within a finite number of steps. The analysis showcases how effectively utilizing the strong convexity assumption leads to superior algorithm performance and theoretical guarantees.

APD Algorithm

#

The APD (Accelerated Primal-Dual) algorithm, a first-order method for convex constrained optimization, is presented. It addresses the problem of minimizing a convex objective function subject to convex constraints. While prior methods exhibited an O(1/ε) convergence rate, APD achieves O(1/√ε) by leveraging primal-dual techniques and acceleration strategies. This improvement is significant, especially in high-dimensional settings where achieving high accuracy is crucial. The algorithm’s effectiveness stems from its ability to handle the duality gap between the primal and dual problems efficiently, effectively leveraging strong convexity when available to accelerate convergence. However, the algorithm’s performance relies on certain assumptions, including Lipschitz smoothness of the functions and knowledge of their smoothness parameters, which may limit its applicability in all problem settings. Further research is needed to explore the algorithm’s robustness and adaptability to more general situations, addressing potential limitations and improving its applicability across various problem types.

Sparsity Pattern

#

The concept of a sparsity pattern, crucial in high-dimensional data analysis, is explored in the context of constrained optimization problems. The paper investigates how the strong convexity of constraint functions impacts the ability of algorithms to efficiently identify the sparsity pattern, which represents the non-zero elements in the optimal solution. A key finding is that leveraging constraint strong convexity leads to faster convergence rates, achieving an improved complexity bound compared to existing methods. This improved rate enables more efficient identification of the sparsity pattern. The paper introduces novel algorithmic techniques, including progressive strong convexity estimation, enhancing the algorithms’ capability. Restart strategies are proposed to further improve efficiency and potentially identify the sparsity pattern within a finite number of steps. The paper explores the theoretical foundation and demonstrates the effectiveness through empirical evaluations focusing on sparsity-inducing applications, such as personalized PageRank, highlighting the practical implications of these findings in high-dimensional settings.

Restart Scheme

#

Restart schemes in optimization algorithms, particularly those dealing with primal-dual methods and strong convexity, aim to improve convergence speed and efficiency. A standard approach involves periodically restarting the algorithm with adjusted parameters, leveraging past information to escape stagnation or accelerate convergence towards optimality. The specific restart criteria are crucial, often based on heuristics or estimates of strong convexity parameters. The scheme’s effectiveness hinges on properly balancing the cost of restarting (potentially losing progress) against the benefit of accelerating convergence. Successful implementations demonstrate finite-time identification of optimal sparsity patterns in applications like sparsity-inducing optimization problems, showcasing the practical value of such methods. However, theoretical analysis must carefully address the interplay between restart frequency, parameter updates, and the overall convergence rate, ensuring that restarts lead to superior performance and avoid unbounded iterations.

Future works

#

The paper’s conclusion alludes to several promising avenues for future research. Extending the adaptive strategy, such as incorporating line search methods, is crucial to enhance the algorithm’s robustness in scenarios where the dual bound is unavailable or difficult to estimate accurately. Further exploration of active-set identification in more general settings is another significant area of investigation, particularly regarding optimization problems with a large number of constraints. The authors also suggest examining the applicability of their methods to problems with more complex or non-smooth objective functions, where proximal operators might be computationally expensive or unavailable. Finally, the potential to improve the theoretical convergence guarantees by refining the strong convexity estimation techniques is a key focus for future development. These future directions could significantly broaden the impact and applicability of the presented algorithms.

More visual insights

#

More on figures

This figure shows the active-set identification accuracy for different algorithms (APD, Mirror-Prox, APDPro, msAPD, APD+restart) on three datasets (bio-CE-HT, bio-CE-LC, econ-beaflw). The x-axis represents the number of iterations, and the y-axis shows the accuracy of identifying the correct sparsity pattern (active set) of the optimal solution. The results demonstrate the superior performance of rAPDPro and msAPD in identifying the active set within a smaller number of iterations compared to other methods.

This figure displays convergence results and feasibility violation for different algorithms (APD, APD+restart, msAPD, Mirror-Prox, and rAPDPro) on three datasets (bio-CE-HT, bio-CE-LC, and econ-beaflw). The top row shows the convergence of the algorithms to the optimum, measured by the relative function value gap. The bottom row illustrates the feasibility violation, indicating how well the algorithms satisfy the constraints.

This figure demonstrates the active-set identification performance of APD, APD+restart, msAPD, rAPDPro and Mirror-Prox on three different datasets. The x-axis shows the number of iterations, while the y-axis represents the accuracy of identifying the sparsity pattern of the optimal solution. rAPDPro and msAPD show superior performance in identifying the active set, converging to high accuracy within a relatively small number of iterations.

More on tables

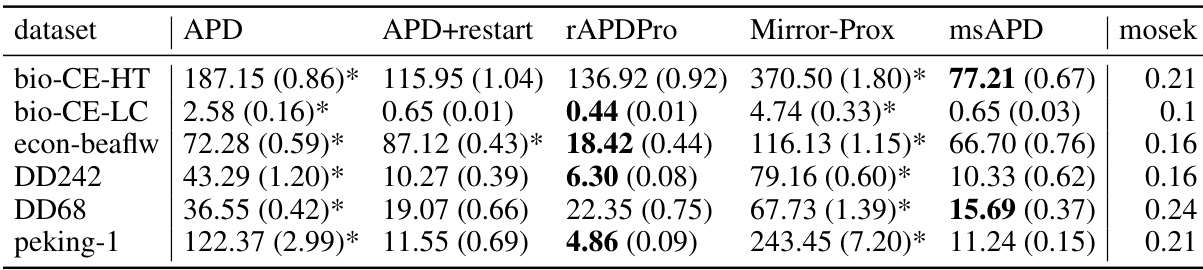
This table summarizes the computational time taken by different algorithms (APD, APD+restart, rAPDPro, Mirror-Prox, msAPD, and mosek) to achieve a relative function value gap and feasibility violation less than 10^-3 for six different datasets. The time is reported in seconds as mean (standard deviation), and an asterisk (*) indicates that the algorithm did not meet the criteria within the allocated iterations. The table provides a comparison of computational efficiency among the methods.

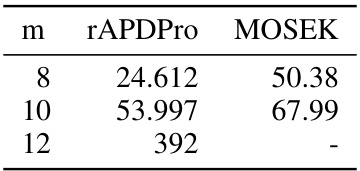
This table compares the computational time in seconds taken by the rAPDPro algorithm and the MOSEK solver to achieve a solution with a specified accuracy for a problem of minimizing the L1 norm subject to multiple strongly convex quadratic constraints. The comparison is performed for different numbers of constraints (m=8, 10, 12). The results show that rAPDPro is faster than MOSEK, especially as the number of constraints increases; MOSEK fails to produce results within a reasonable time when the number of constraints reaches 12.

Full paper

#