Mixture of Scales: Memory-Efficient Token-Adaptive Binarization for Large Language Models

↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in LLM compression as it presents BinaryMoS, a novel binarization technique that significantly improves the accuracy of binarized LLMs while maintaining memory efficiency. Its token-adaptive approach offers a new direction for tackling the accuracy loss problem commonly associated with binarization, paving the way for more efficient and powerful LLMs in resource-constrained environments. The detailed analysis and comparison with other state-of-the-art methods also provides valuable insights and benchmarks for future research in LLM optimization.

Visual Insights

#

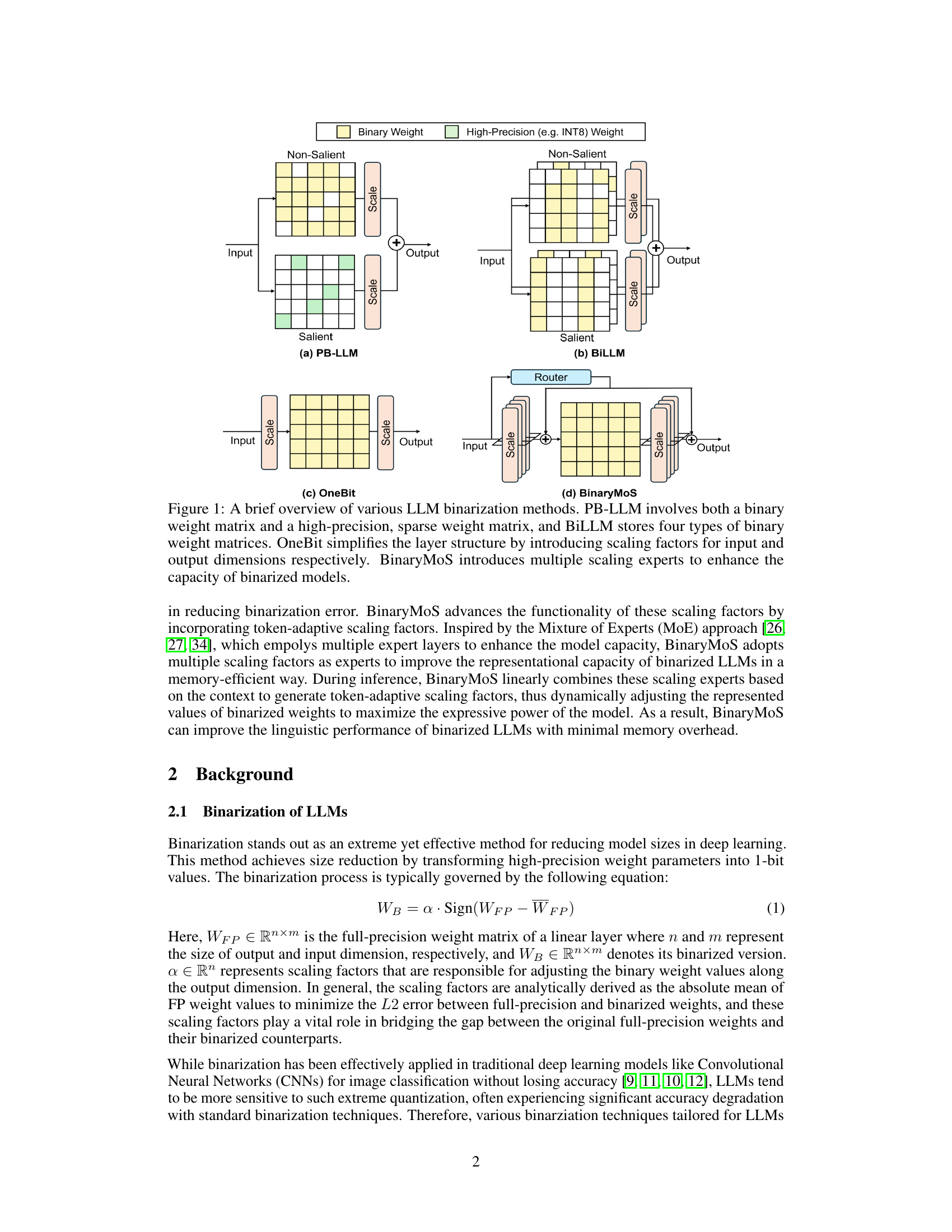
This figure provides a visual comparison of four different LLM binarization methods: PB-LLM, BiLLM, OneBit, and BinaryMoS. Each method is illustrated with a diagram showing its approach to handling binary and high-precision weights. PB-LLM uses a combination of both, BiLLM uses multiple types of binary matrices, OneBit uses scaling factors on both input and output, and BinaryMoS uses multiple scaling experts. The diagrams highlight the differences in architectural complexity and the strategies used to improve the accuracy of binarized models.

This table compares the memory usage of large language models (LLMs) when using different quantization methods. It shows the memory footprint in GB for Float16 (full precision) and four different binarization techniques (PB-LLM, BiLLM, OneBit, and BinaryMoS) across two different LLaMA model sizes (7B and 13B parameters). The numbers in parentheses indicate the compression ratio achieved by each binarization method compared to the full-precision Float16 model. This highlights the space savings offered by various binarization approaches, demonstrating the efficiency of BinaryMoS in reducing the memory needed for LLMs while maintaining performance.

In-depth insights

#

BinaryMoS Intro

#

BinaryMoS, introduced as a memory-efficient token-adaptive binarization technique for LLMs, presents a novel approach to address the limitations of traditional binarization methods. Unlike conventional methods using static scaling factors, BinaryMoS employs multiple scaling experts, dynamically merging them for each token. This token-adaptive strategy significantly boosts the representational power of binarized LLMs by enabling contextual adjustments to binary weights. Crucially, this adaptive process only affects scaling factors, not the entire weight matrix, preserving the compression efficiency of static binarization. The integration of multiple scaling experts, inspired by Mixture of Experts (MoE) architecture, enhances model capacity while maintaining memory efficiency. BinaryMoS, therefore, strikes a balance between enhanced accuracy and memory-efficient compression, overcoming a key limitation of previous binarization techniques that severely compromise LLM performance. The innovative router design in BinaryMoS is key to dynamically combining scaling experts based on context, enabling the creation of effectively infinite, token-adaptive scaling factors.

MoE Adaptation

#

MoE adaptation in large language model (LLM) binarization presents a compelling approach to enhance accuracy without significantly increasing model size. The core idea is to leverage the power of Mixture of Experts (MoE) to dynamically adjust scaling factors for each token rather than using static scaling. This token-adaptive approach, unlike traditional methods, allows for contextual adjustments to binary weights, leading to improved expressiveness. The key lies in training multiple scaling experts, or ‘MoE experts’, which capture different aspects of the input data. A gating network then dynamically selects and combines these experts based on the context of each token. This approach increases representational power while maintaining compression efficiency because it only involves manipulating lightweight scaling factors rather than the entire weight matrix. While introducing additional parameters for the gating network and multiple scaling experts, the significant gains in model accuracy often offset this memory overhead, offering a balance between efficiency and effectiveness. Therefore, the strategy presents a promising avenue for bridging the accuracy gap between full-precision LLMs and binarized models, making binarization a more feasible option for deployment on resource-constrained devices.

Compression Gains

#

The concept of “Compression Gains” in the context of large language models (LLMs) centers on reducing model size without significant performance degradation. This is crucial for deploying LLMs on resource-constrained devices. Achieving substantial compression gains typically involves techniques like weight quantization, where the precision of model weights is reduced (e.g., from 32-bit floating point to 1-bit binary). However, aggressive compression often leads to accuracy loss. Therefore, the key challenge lies in developing methods that balance compression ratios with the preservation of model accuracy. This often requires exploring novel quantization techniques or employing techniques like knowledge distillation to mitigate the information loss inherent in compression. The effectiveness of different compression strategies is highly dependent on the specific LLM architecture and the downstream tasks. Measuring compression gains involves comparing model sizes and performance metrics (like perplexity) before and after applying compression techniques. Ultimately, the pursuit of substantial compression gains is about making LLMs more accessible and efficient for a wider range of applications.

Token-Adaptive

#

The concept of ‘Token-Adaptive’ in the context of large language model (LLM) binarization signifies a paradigm shift from traditional static methods. Instead of applying a single scaling factor to all weight parameters uniformly, a token-adaptive approach dynamically adjusts these factors based on the specific token being processed. This allows for contextual sensitivity, meaning the model’s response is more nuanced and attuned to the particular word or sub-word unit. The key benefit is enhanced representational power, enabling the model to maintain accuracy despite the extreme compression of binarization, which typically sacrifices precision. The adaptive nature of this method offers a more expressive LLM, capable of capturing subtle linguistic nuances. However, a potential drawback is the increased computational overhead associated with dynamically calculating these context-dependent scaling factors; the paper’s success lies in demonstrating efficiency gains despite this increased complexity. This approach suggests a promising direction for future research in efficient LLM compression, focusing on methods that prioritize adaptive representation.

Future Work

#

The paper’s lack of a dedicated ‘Future Work’ section is notable. However, the conclusion hints at several promising avenues. Extending the Mixture of Scales (MoS) approach to multi-bit quantization is a logical next step, leveraging the inherent scaling factor mechanisms already present. This would broaden the applicability and potentially improve the accuracy further. Another crucial area is integrating advanced training techniques from the Mixture of Experts (MoE) literature, such as specialized routing functions or balanced token assignment. This could significantly enhance the performance of BinaryMoS. Finally, addressing the remaining accuracy gap between binarized and full-precision models remains a key challenge. While BinaryMoS shows impressive results, further research into overcoming the limitations inherent in extreme quantization is necessary for widespread adoption. Investigating alternative quantization strategies or exploring new architectures better suited to binarization could yield valuable advancements.

More visual insights

#

More on figures

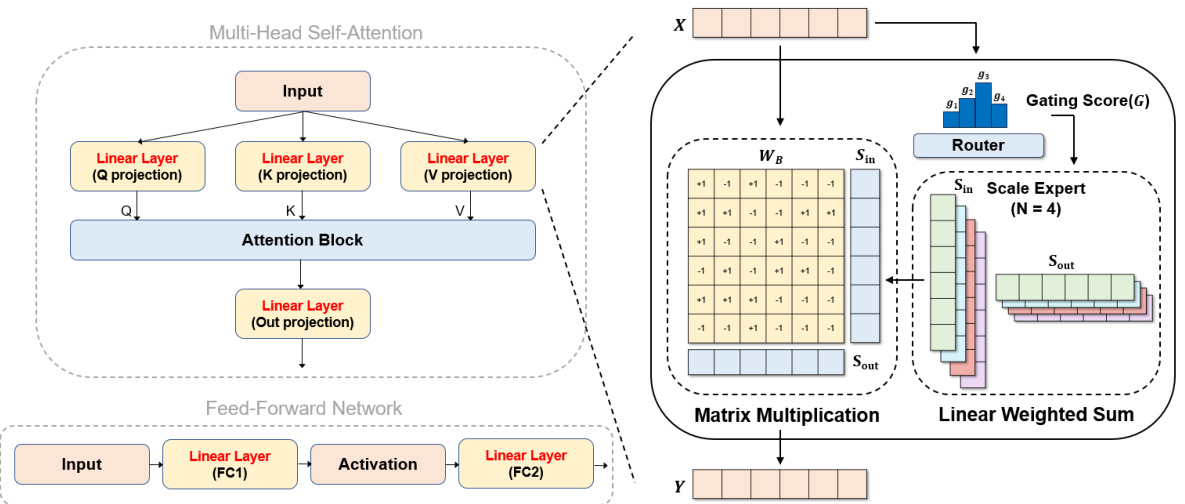
This figure illustrates the architecture of BinaryMoS, a novel binarization technique for LLMs. It shows how multiple scaling experts are used to generate token-adaptive scaling factors, which are then used to improve the representational power of binarized LLMs. The figure highlights the key components of BinaryMoS, including the router, which dynamically combines the scaling experts, and the matrix multiplication and linear weighted sum operations, which are used to generate the final output. The figure also shows how BinaryMoS maintains compression efficiency while achieving better accuracy than traditional static binarization methods.

This figure shows the gating scores for four scaling experts and resulting token-adaptive scaling factors for the output projection of the 18th layer in the LLaMA-1-7B model. The top panel (a) shows a heatmap visualizing how the gating scores vary across tokens in a sequence, indicating how the model dynamically weights the influence of different scaling experts for each token. The bottom panel (b) presents boxplots illustrating the distribution of token-adaptive scaling factors for both input and output dimensions, comparing them against the use of a single scaling factor. The boxplots highlight the increased variability and range of values achieved with the token-adaptive approach, demonstrating its effectiveness in capturing contextual information.

More on tables

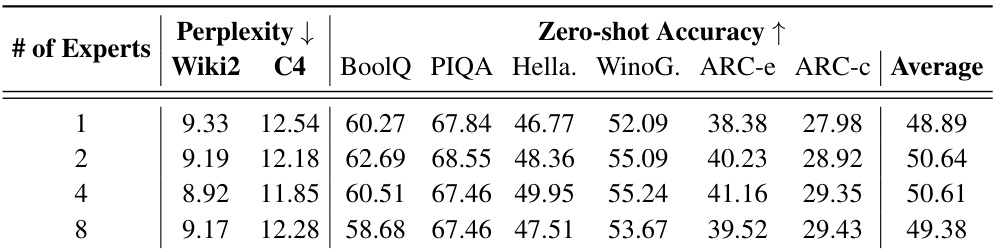
This table presents the results of an experiment to determine the optimal number of scaling experts for the BinaryMoS model. The experiment used the LLaMA-1-7B model and only one-third of the training data for faster assessment. The table shows the perplexity and zero-shot accuracy results for different numbers of scaling experts (1, 2, 4, and 8). Lower perplexity values and higher zero-shot accuracy indicate better model performance. The results suggest that using 4 scaling experts provides the optimal balance between performance improvement and increased model complexity.

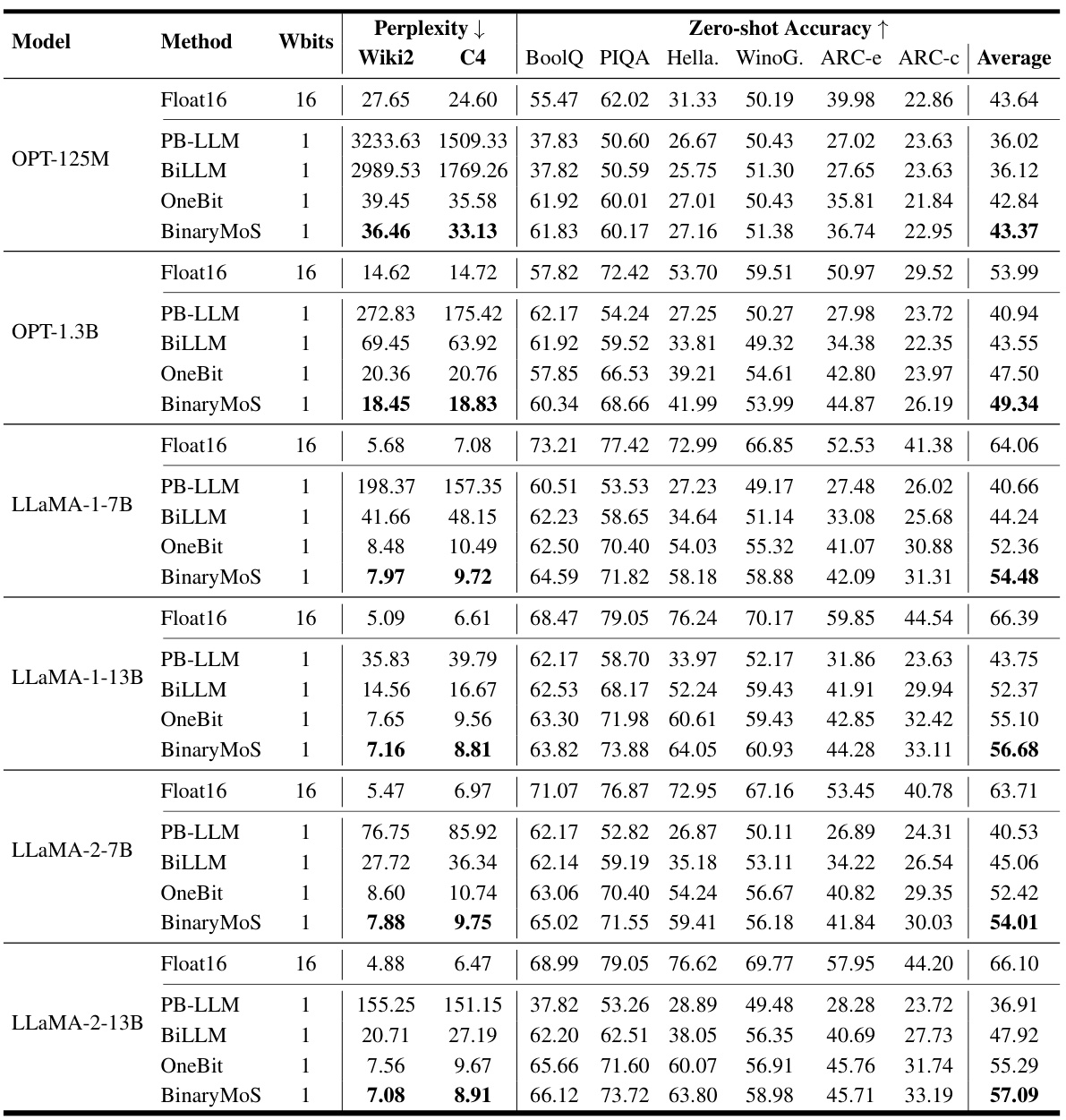
This table presents a comparison of the performance of Float16 and various binarized LLMs across different language modeling tasks. It shows perplexity scores (lower is better) on Wiki2 and C4 datasets and zero-shot accuracy (higher is better) on several benchmark datasets (BoolQ, PIQA, HellaSwag, Winogrande, ARC-e, ARC-c). The table allows for a detailed comparison of the effectiveness of different binarization techniques (PB-LLM, BiLLM, OneBit, and BinaryMoS) in maintaining performance while reducing model size.

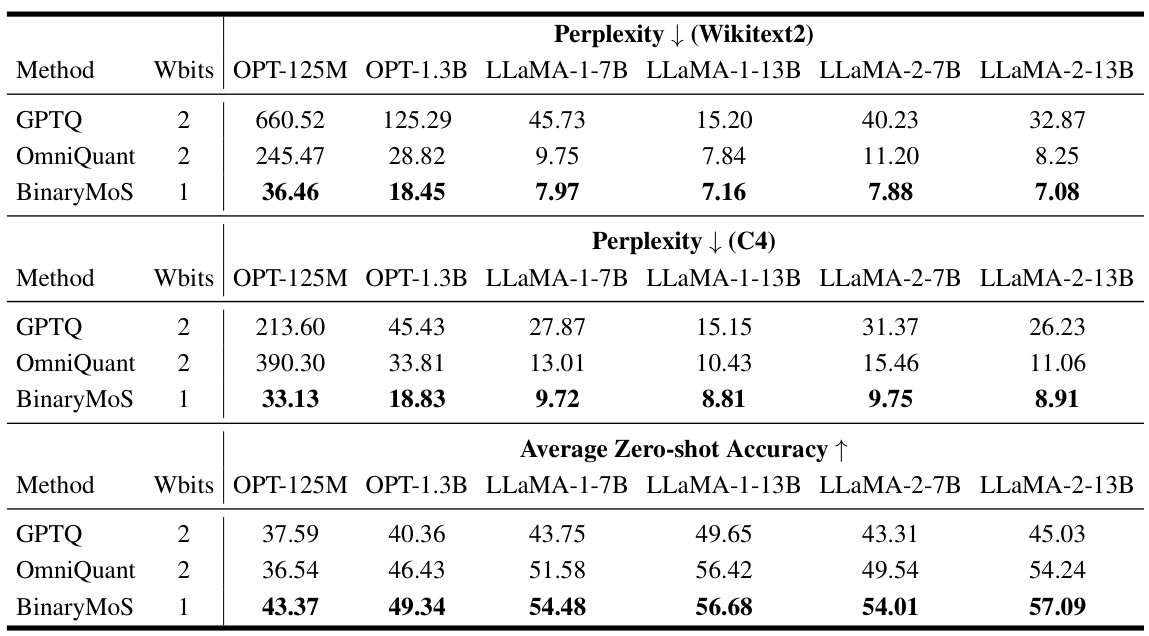
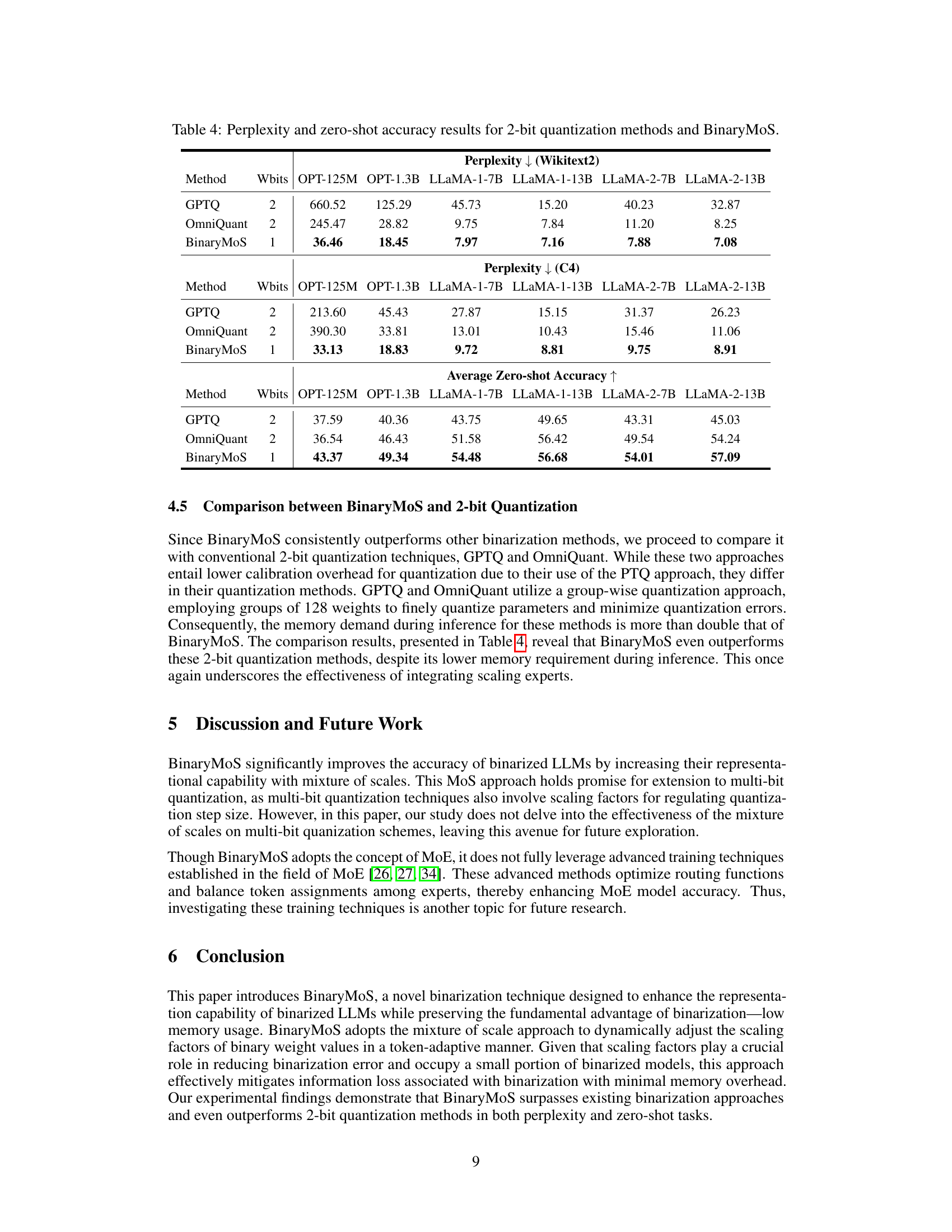
This table compares the performance of BinaryMoS against two other 2-bit quantization methods (GPTQ and OmniQuant) across various LLMs. It shows perplexity scores on the WikiText2 and C4 datasets, as well as average zero-shot accuracy across several downstream tasks. The results demonstrate that BinaryMoS achieves lower perplexity and higher zero-shot accuracy compared to the other 2-bit quantization methods, highlighting its effectiveness in improving the accuracy of binarized LLMs.

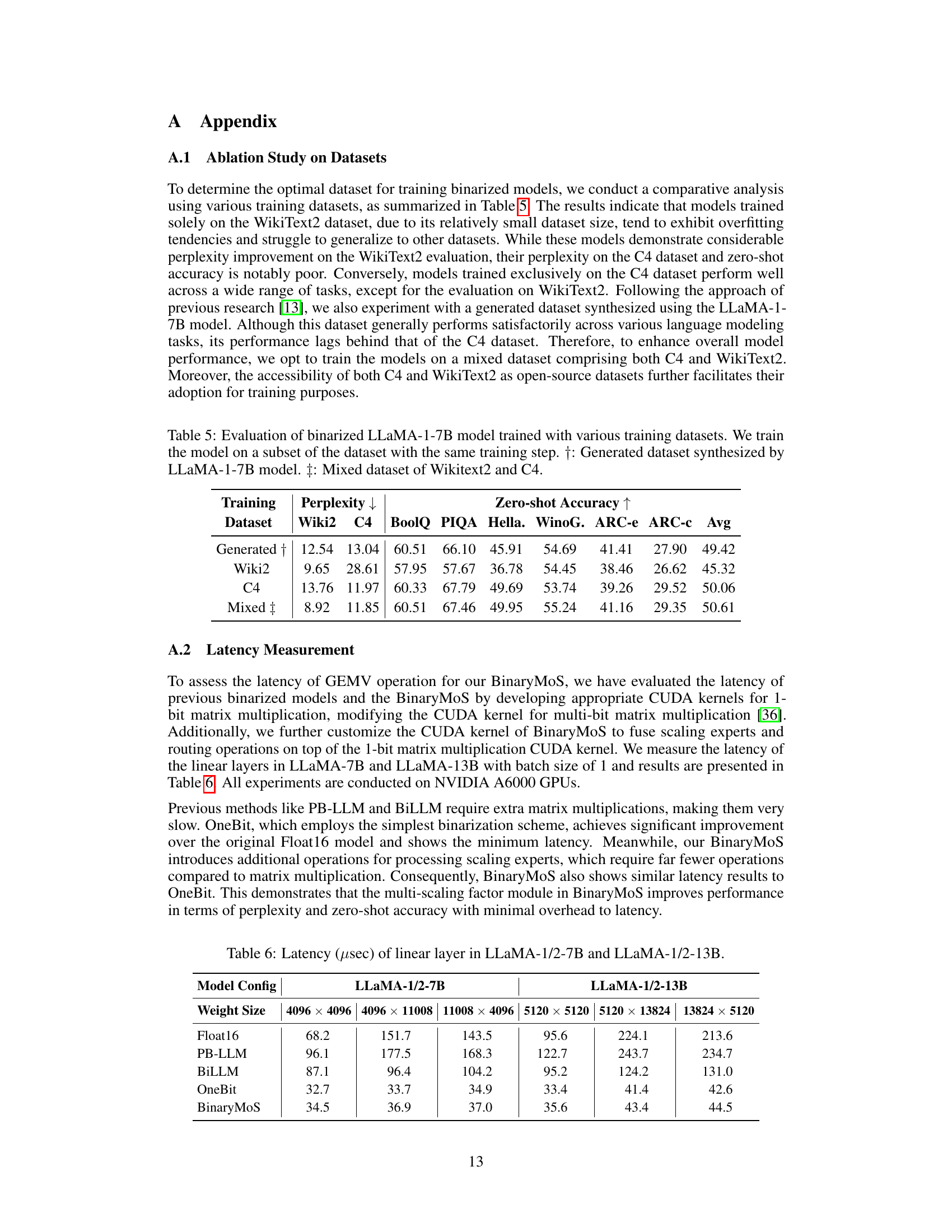
This table presents the results of an ablation study on the choice of training dataset for a binarized LLaMA-1-7B language model. It compares the performance of models trained on three different datasets: the WikiText2 dataset, the C4 dataset, and a synthetic dataset generated by the LLaMA-1-7B model. For each dataset, the table shows perplexity scores on the WikiText2 and C4 datasets, as well as zero-shot accuracy on various common sense reasoning tasks (BoolQ, PIQA, HellaSwag, WinoGrande, ARC-e, ARC-c). The table helps determine the optimal dataset for training binarized models and demonstrates that a mixed dataset comprising both the C4 and WikiText2 datasets provides the best balance of performance across different tasks.

This table presents the latency in microseconds (µsec) of the linear layer operations for various LLM binarization methods, including Float16 (baseline), PB-LLM, BiLLM, OneBit, and BinaryMoS. The latency is measured for two different LLaMA models: LLaMA-1/2-7B and LLaMA-1/2-13B, each with three different weight sizes. The results show the impact of the different binarization techniques on inference speed.

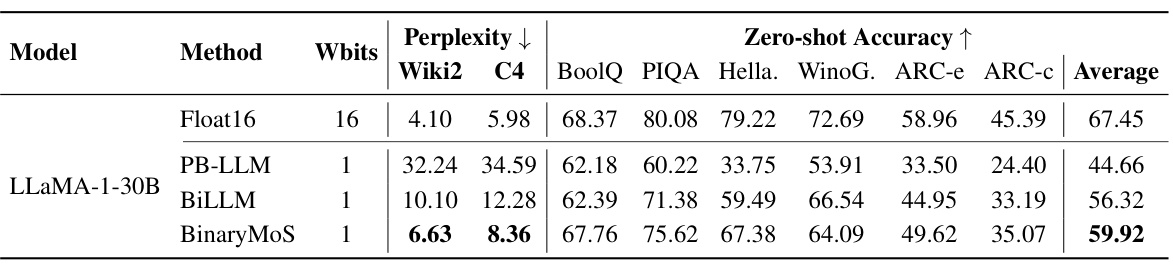
This table presents the results of perplexity and zero-shot accuracy for the LLaMA-1-30B model using different binarization methods (PB-LLM, BiLLM, BinaryMoS) and the Float16 baseline. It shows the perplexity scores on the Wiki2 and C4 datasets, and zero-shot accuracy scores across various reasoning tasks (BoolQ, PIQA, HellaSwag, WinoGrande, ARC-e, ARC-c). The results demonstrate the relative performance of each method in terms of maintaining linguistic capabilities while achieving model compression.

Full paper

#