On Sampling Strategies for Spectral Model Sharding

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in federated learning, particularly those tackling data heterogeneity and resource constraints. It offers novel sampling strategies for spectral model sharding, improving efficiency and performance. Its closed-form solutions simplify implementation, and its empirical results on various datasets showcase its effectiveness. This work opens avenues for researching improved sampling techniques and optimization strategies in the federated learning setting.

Visual Insights

#

This figure compares the communication efficiency and diversity of different sampling strategies used for spectral model sharding. The x-axis represents the number of communication rounds, and the y-axis on the left shows the test accuracy of a ResNet model on CIFAR-100. The y-axis on the right shows the average normalized marginal entropy (ANME), a measure of how diverse the sampling strategy is. High ANME indicates exploration, while low ANME indicates exploitation. The figure shows that the original PriSM method is highly explorative, while the proposed ‘unbiased’ modification makes it more exploitative, leading to better performance in limited computation settings. The proposed Unbiased and Collective strategies show a balance between exploration and exploitation.

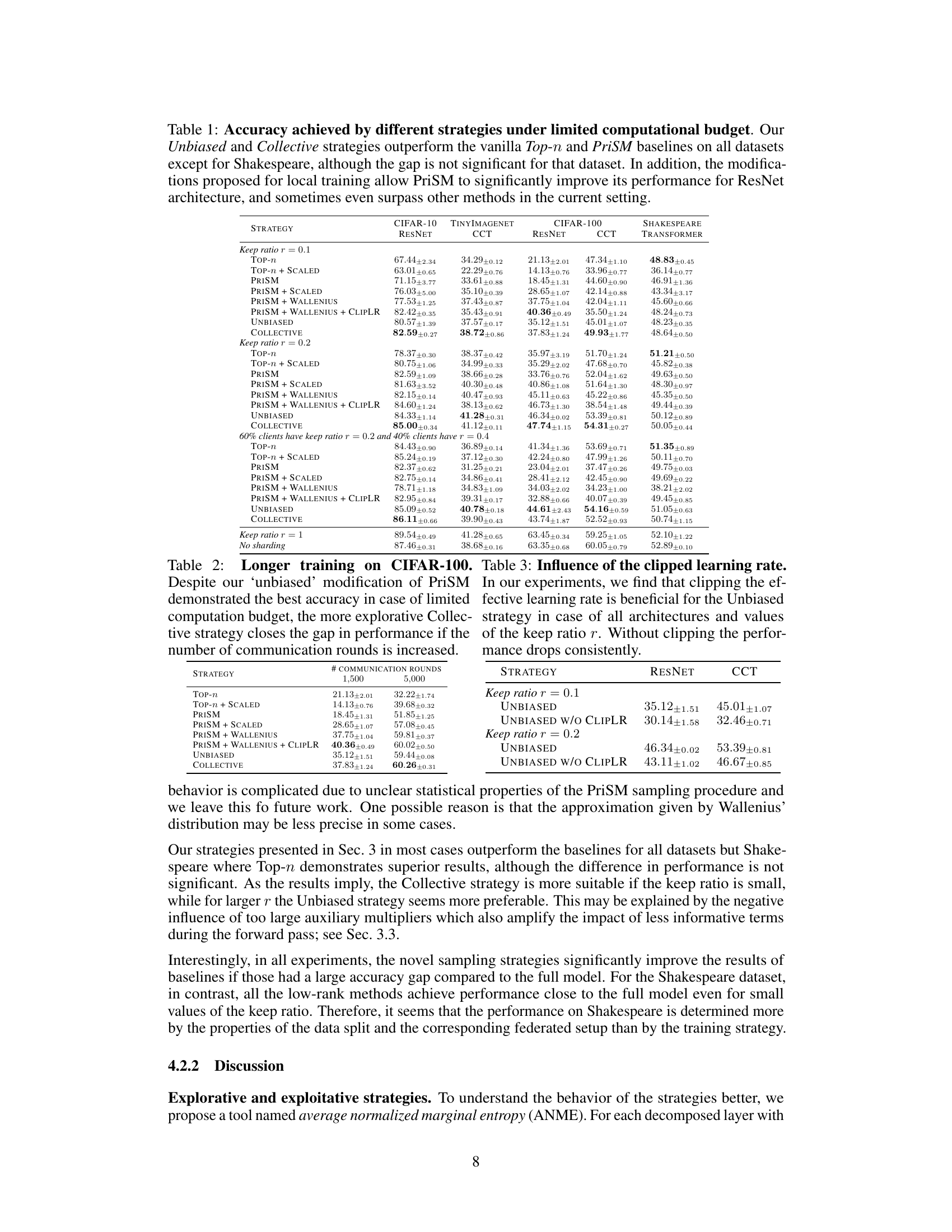
This table presents the accuracy results of different model sharding strategies on various datasets (CIFAR-10, TinyImagenet, CIFAR-100, Shakespeare). It compares the performance of two novel strategies (Unbiased and Collective) against existing methods (Top-n and PriSM), considering different keep ratios (the proportion of model parameters used). The results show the impact of both the sampling strategy and modifications to local training on model accuracy, highlighting the superior performance of the proposed methods in many scenarios.

In-depth insights

#

Spectral Model Sharding

#

Spectral model sharding addresses the challenge of heterogeneous clients in federated learning by partitioning model parameters into low-rank matrices. This is achieved through singular value decomposition (SVD), enabling efficient on-device training. Two key sampling strategies are presented: one producing unbiased estimators of original weights, the other minimizing squared approximation error. These are formulated as solutions to optimization problems. Practical considerations for federated learning, such as local training and aggregation, are also discussed. Empirical results show improved performance across various datasets, highlighting the effectiveness of these novel sampling strategies. The work offers a principled approach to overcome the heuristic nature of existing methods, leading to more robust and efficient federated learning systems. The focus on unbiased estimation and error minimization provides a strong theoretical foundation for the proposed approach.

Sampling Strategies

#

The core of this research paper revolves around developing novel sampling strategies for spectral model sharding in federated learning. The authors cleverly address the challenge of heterogeneous clients with varying computational capabilities by proposing two distinct strategies. The first focuses on creating unbiased estimators of the original model weights, drawing inspiration from inverted dropout regularization. This approach ensures that the sampled model remains a faithful representation of the original, avoiding systematic bias. The second strategy prioritizes minimizing the squared approximation error, effectively balancing bias and variance to improve model accuracy. Both strategies are formulated as solutions to specific optimization problems, providing a principled approach rather than relying on heuristics. A key contribution is the closed-form solutions enabling efficient computation on the server-side, minimizing the load on resource-constrained client devices. The paper further explores the practical implications of these strategies within a federated learning setting, discussing local training considerations and empirically demonstrating improved performance across various datasets.

Unbiased Estimation

#

The concept of unbiased estimation, within the context of spectral model sharding for federated learning, centers on creating estimators of the original model weights that, on average, do not systematically over- or underestimate the true values. This is achieved by carefully selecting which components from the singular value decomposition (SVD) of the weight matrices to include in the sharded model. The authors propose a solution inspired by dropout regularization, assigning inclusion probabilities inversely proportional to the magnitude of the singular values, which leads to an unbiased estimator. This approach is mathematically elegant, ensuring that the expected value of the sharded model perfectly matches the original model weights. However, the practical implication is that the variance of the estimator can be high. The unbiased estimator is presented as a closed-form solution to a specific optimization problem, minimizing the expected Frobenius norm discrepancy between the estimator and the original weights, subject to the unbiasedness constraint.

Collective Estimation

#

The concept of “Collective Estimation” in the context of spectral model sharding for federated learning presents a compelling approach to address the challenges of heterogeneous clients. Instead of treating each client’s sub-model independently, it leverages information from multiple clients to collaboratively reconstruct the full model weights. This approach is particularly valuable when dealing with a significant number of clients, offering robustness and improved accuracy. By combining multiple unbiased estimations, it aims to reduce variance and improve the quality of the overall approximation. The method involves aggregating the updates from multiple clients, strategically weighting each client’s contribution based on its dataset size and the relative importance of the sampled model components. This approach requires careful consideration of weighting schemes and potential biases; the paper’s exploration of optimizing the inclusion probabilities and auxiliary weights suggests a refined strategy for achieving a balance between bias and variance. The success of this technique hinges on the assumption of independence and identical distribution of the clients’ sub-models, an assumption that may not always hold in practice. However, the potential gains in terms of model accuracy and robustness are significant, making it a worthwhile approach to explore and potentially refine in future research.

Future Work

#

The paper’s exploration of spectral model sharding for federated learning paves the way for several exciting avenues of future research. Improving the convergence speed of the proposed unbiased and collective estimators is paramount. The current methods, while demonstrating accuracy improvements, could benefit from techniques to accelerate the training process, possibly through adaptive learning rate scheduling or more sophisticated optimization algorithms. Investigating the interaction between joint sampling distribution choices and model performance is also crucial. While the paper uses the Conditional Poisson scheme, exploring alternatives and their impact on accuracy and generalizability remains open. A deeper analysis of the impact of data heterogeneity on the effectiveness of different sampling strategies is warranted. The study hints at a complex interplay between data distribution and model performance, highlighting the need for a more in-depth theoretical understanding and tailored strategies. Finally, extending the framework to handle more complex model architectures and a wider range of federated learning scenarios is crucial to establish the broad applicability of this spectral model sharding technique. The incorporation of advanced architectural features and a broader scope would significantly expand the potential impact of this work.

More visual insights

#

More on figures

This figure shows the average normalized marginal entropy (ANME) for different sampling strategies across communication rounds. ANME measures the diversity of samples selected by each strategy; high ANME indicates high diversity (exploration) and low ANME suggests low diversity (exploitation). PriSM initially shows high ANME (exploratory), while the modification using Wallenius’ method shifts it towards lower ANME (exploitative). Other strategies such as Unbiased and Collective occupy intermediate positions. The figure suggests that a balance between exploration and exploitation is needed to optimize performance, especially with limited computational resources.

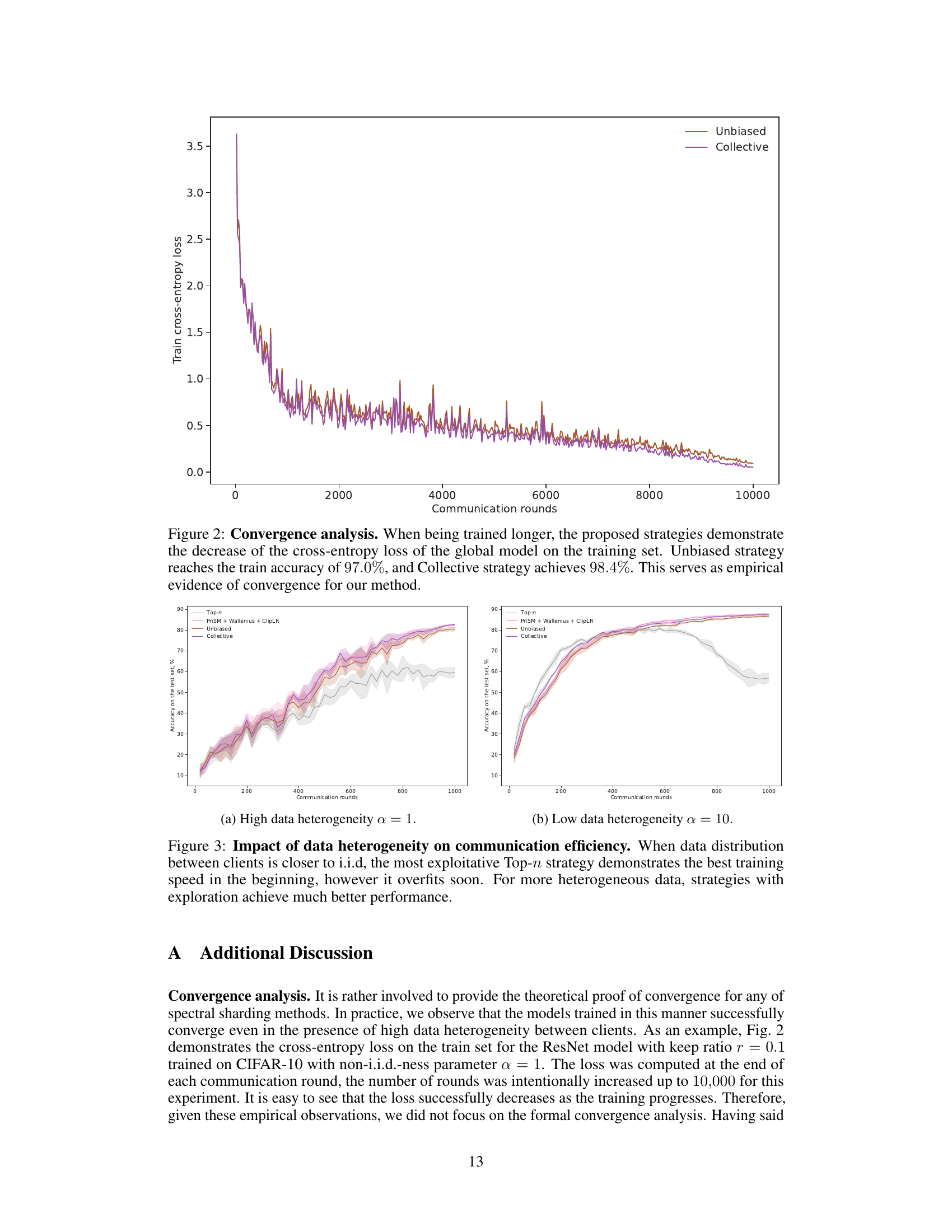
This figure shows the convergence behavior of the proposed Unbiased and Collective sampling strategies during the training process. The x-axis represents the number of communication rounds, and the y-axis represents the train cross-entropy loss. The plot demonstrates that both strategies effectively reduce the training loss over an extended training period, reaching high training accuracies (97.0% and 98.4%, respectively). This visual evidence supports the claim that both strategies lead to model convergence.

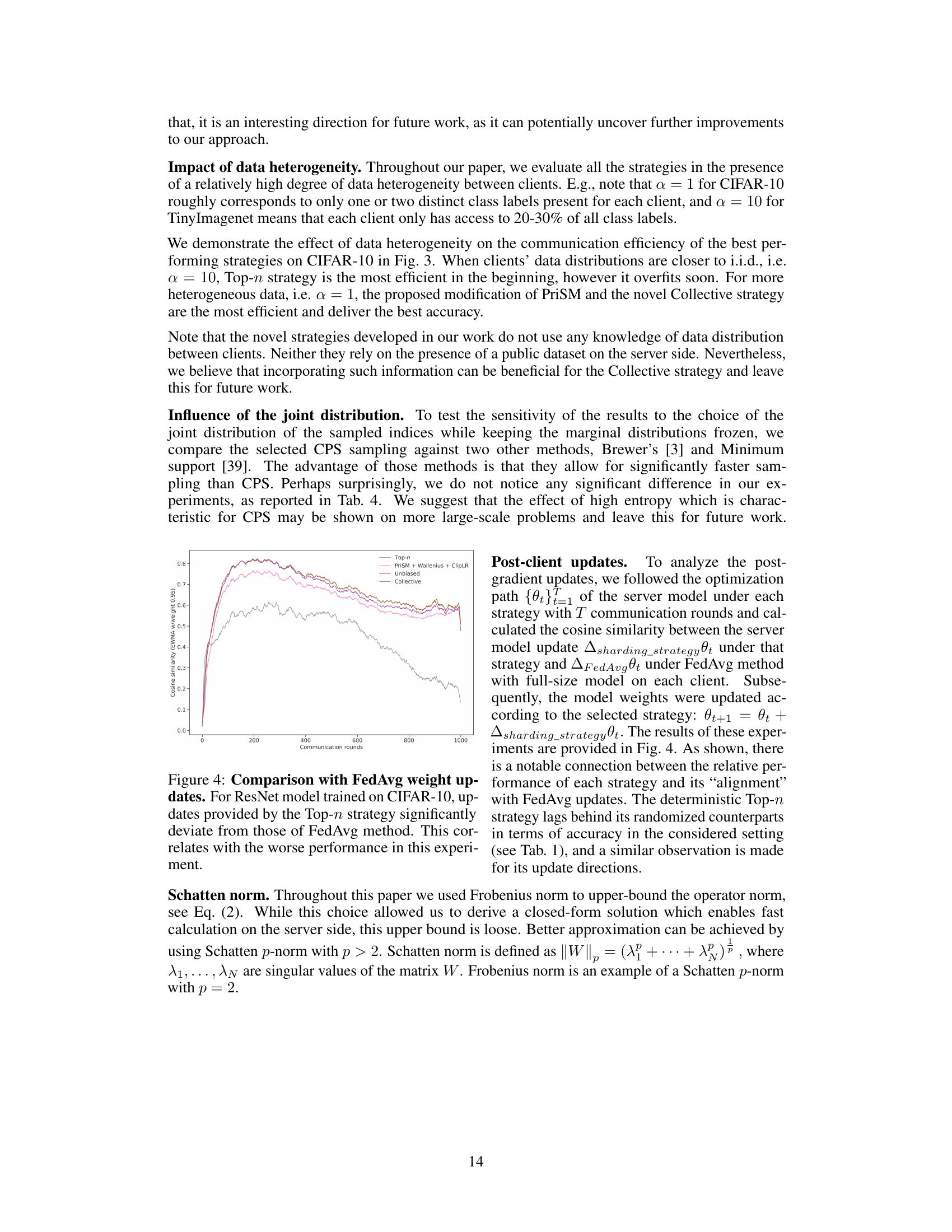
This figure shows the accuracy on the test set for different strategies (Top-n, PriSM + Wallenius + ClipLR, Unbiased, and Collective) across different communication rounds for two scenarios: high data heterogeneity (α = 1) and low data heterogeneity (α = 10). The results highlight how the choice of strategy impacts model performance differently depending on the level of data heterogeneity between clients. With high heterogeneity, the more explorative strategies (Unbiased and Collective) eventually outperform Top-n, while with low heterogeneity, Top-n shows initial advantage but overfits.

This figure compares the optimization path of FedAvg with different spectral model sharding strategies. The cosine similarity (using an exponentially weighted moving average with a weight of 0.95) is calculated between the server model updates for each strategy and the FedAvg updates. The results show a significant divergence in the Top-n strategy, indicating its deviation from the FedAvg approach and potentially contributing to its lower performance.

More on tables

This table compares the performance of different model sharding strategies on various datasets under limited computational resources. The strategies include Top-n, PriSM (with and without modifications), Unbiased, and Collective. Accuracy is reported for different keep ratios, showing the effectiveness of the novel Unbiased and Collective methods in improving model accuracy compared to existing techniques.

This table compares the performance of different model sharding strategies (Top-n, PriSM, Unbiased, and Collective) on various datasets (CIFAR-10, TinyImagenet, CIFAR-100, Shakespeare) under different keep ratios (0.1, 0.2, and a heterogeneous setup with 60% clients having keep ratio 0.2 and 40% with 0.4). The results showcase that the proposed Unbiased and Collective strategies generally outperform the baselines, particularly for ResNet models. Modifications to the PriSM strategy, inspired by the Unbiased method, also yield improvements.

This table presents the accuracy results of different model sharding strategies on various datasets (CIFAR-10, TinyImagenet, CIFAR-100, Shakespeare) with limited computational resources. It compares the performance of the proposed ‘Unbiased’ and ‘Collective’ strategies against baseline methods (Top-n and PriSM), showing the impact of different sampling strategies and training modifications on the accuracy of the models.

Full paper

#