↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many current methods for posterior sampling lack quantitative guarantees, hindering their use in scientific applications where reliability is critical. This is especially true in high-dimensional settings, where the posterior distribution can be extremely complex and difficult to sample from directly, even with prior information from denoising oracles. The limitations of existing methods are highlighted, emphasizing the need for robust and principled approaches.
This paper tackles this challenge by developing a novel technique called ’tilted transport’. This method cleverly transforms the original posterior sampling problem into a new one that is provably easier to sample from, leveraging the quadratic structure of the log-likelihood in linear inverse problems and the denoising oracle to perform this transformation. The authors provide theoretical conditions under which the transformed posterior is strongly log-concave, ensuring efficient sampling using standard methods. They validate their approach on both Ising models and high-dimensional Gaussian mixture models, demonstrating its effectiveness in matching or exceeding the performance of state-of-the-art sampling methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on Bayesian inverse problems and high-dimensional data generation. It bridges the gap between theoretical understanding and practical application of score-based diffusion models, offering a novel approach to posterior sampling with provable guarantees. This work is relevant to current research trends in machine learning, statistical physics, and scientific computing, opening new avenues for efficient and reliable inference in complex systems.
Visual Insights#
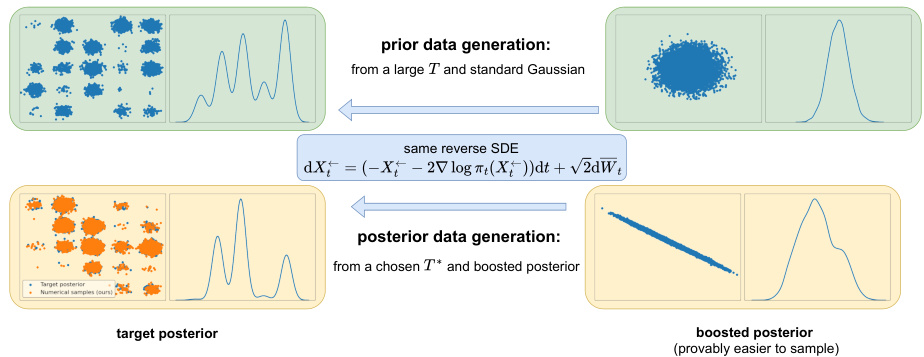
This figure illustrates the tilted transport method for boosting posterior sampling using a 2D Gaussian mixture model. It compares the original multimodal target posterior distribution with the transformed, unimodal boosted posterior distribution, which is easier to sample from. The figure shows the density plots of the first variable for each distribution, and corresponding scatter plots of numerical samples generated using the tilted transport method.

The table presents the results of applying the proposed tilted transport method to a Gaussian mixture model with varying dimensionality (d) and reduced observation dimensionality (d’). The results are compared against those obtained using Langevin dynamics and the HMC sampler, demonstrating the improved sampling performance of the proposed method. Specifically, the table shows the sliced Wasserstein distances between the samples generated by each method and the true posterior distribution. The results showcase the effectiveness of the proposed tilted transport approach in efficiently sampling the posterior distribution, even in high-dimensional settings.
In-depth insights#
Posterior Sampling#
Posterior sampling, a core problem in Bayesian inference, seeks to generate samples from a probability distribution representing the posterior belief about a parameter given observed data. This is often computationally challenging, especially in high-dimensional spaces. The paper explores this challenge, demonstrating the intractability of posterior sampling using generic methods. A key obstacle is the ill-conditioning of measurement operators, making naive approaches infeasible. To overcome this, a novel method called ’tilted transport’ is proposed, leveraging the quadratic structure of the log-likelihood to transform the posterior into a more easily sampled distribution. This is achieved by carefully constructing a time-varying quadratic transformation that leverages existing prior denoising oracles. The method’s efficacy is rigorously validated on Gaussian mixture models and Ising models, showcasing its effectiveness even in high-dimensional settings and matching the performance of state-of-the-art algorithms. The strong log-concavity of the transformed posterior under specific conditions is proven, guaranteeing efficient sampling.
Tilted Transport#
The core idea of “Tilted Transport” is to cleverly transform a challenging posterior distribution in a Bayesian inference problem into a more tractable one. This is achieved by leveraging the quadratic structure inherent in many inverse problems, combined with a pre-trained denoising oracle (score-based model). The method precisely maps the original posterior sampling problem to a new one, where sampling becomes provably easier. This transformation involves a carefully designed time-varying quadratic tilt, modifying the posterior’s geometry to enhance its log-concavity. A key condition for success is the interplay between the prior’s spread (tilted spread) and the measurement matrix’s condition number and signal-to-noise ratio (SNR). The framework elegantly bridges the gap between principled data generation via diffusion models and principled posterior inference, offering provable guarantees where heuristics often fail. The method’s power lies in its ability to transfer the efficiency of sampling from the prior to sampling the posterior, leading to improved performance across different high-dimensional applications.
Hardness Results#
The section on Hardness Results likely demonstrates the inherent computational challenges in posterior sampling for high-dimensional data. It might present a proof or theoretical argument showing that no efficient, general-purpose algorithm can solve the problem under certain conditions, especially when dealing with ill-conditioned measurement matrices. This is crucial because it establishes the need for the novel methods proposed in the paper. The results likely focus on the limitations of straightforward approaches that directly use the denoising oracle without additional techniques, emphasizing that the posterior distribution’s complexity increases drastically with dimensionality. Therefore, the Hardness Results section sets the stage by justifying the need for the more sophisticated and theoretically grounded tilted transport method presented as a solution to the intractable problem, paving the way to show the advantages of the proposed algorithm in overcoming such inherent limitations.
Ising Model Tests#
An analysis of the ‘Ising Model Tests’ section within a research paper would ideally delve into how well the proposed method handles a canonical problem in statistical physics. The Ising model, with its binary variables and interactions, serves as a stringent test for algorithms due to its high dimensionality and complex, often multimodal, probability distributions. A strong section would showcase the algorithm’s efficiency in comparison to known baselines like Glauber dynamics, highlighting its ability to reach thermal equilibrium quickly and accurately. Quantitative results, such as the computational cost scaling with system size, would be crucial, demonstrating practical applicability. Furthermore, the analysis should address limitations; for instance, exploring the model’s behavior near critical thresholds and clarifying whether the efficiency holds for different interaction strengths. A thoughtful discussion of whether the method matches or surpasses state-of-the-art performance for Ising model sampling is also warranted. Finally, the section should clearly state if the test is used to confirm theoretical findings or primarily to demonstrate practical applicability of the method.
Future Directions#
Future research could explore extending tilted transport to nonlinear inverse problems, moving beyond the current linear constraint. Investigating the conditions under which dimension dependence in the spread function can be removed is crucial for scalability. Developing efficient algorithms based on the continuous-time framework presented, possibly integrating advanced numerical methods, would be valuable. Furthermore, exploring the interplay between tilted transport and existing posterior sampling methods could lead to hybrid approaches with improved performance in various regimes. Finally, a comprehensive empirical evaluation across diverse high-dimensional datasets and complex inverse problems is needed to solidify the practical impact of tilted transport.
More visual insights#
More on figures
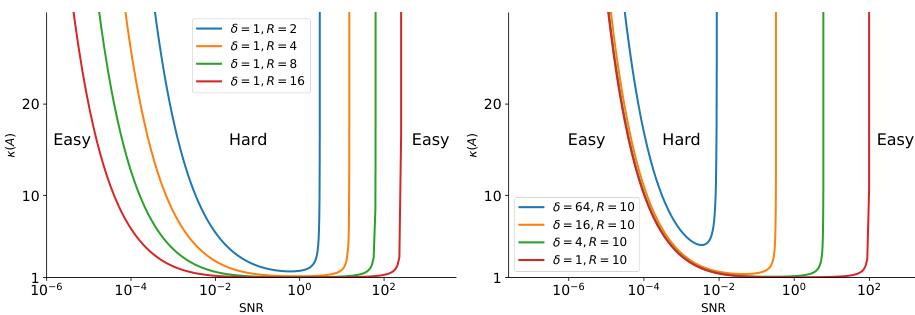
This figure shows a phase diagram illustrating the conditions under which the boosted posterior, vT*, becomes strongly log-concave. The x-axis represents the signal-to-noise ratio (SNR), and the y-axis represents the condition number, κ(A), of the measurement matrix. Each U-shaped curve represents a different combination of parameters δ (variance of the Gaussian component in the Gaussian mixture prior) and R (radius of the support of the Gaussian mixture prior). The region outside a curve indicates that the boosted posterior is strongly log-concave under those conditions, making it easier to sample from. The diagram showcases how the difficulty of posterior sampling depends on both the SNR and the condition number of A, and how the prior’s properties also play a role.

This figure compares the performance of Langevin dynamics and the proposed tilted transport method for posterior sampling using a Gaussian mixture prior. The y-axis shows the sliced Wasserstein distance, a metric measuring the difference between the sampled and true posterior distributions. The x-axis shows the signal-to-noise ratio (SNR). Three panels represent different dimensions (d=20, 40, 80). The plot shows that the tilted transport method significantly reduces the error compared to the standard Langevin approach, particularly in low and mid-SNR regimes.

This figure illustrates the tilted transport method for boosting posterior sampling using a 2D Gaussian mixture model. It compares the original target posterior distribution (multimodal and difficult to sample from) with the transformed, boosted posterior distribution (unimodal and easier to sample). The density plot shows the marginal distribution of the first variable, highlighting the difference in shape between the original and boosted posteriors. The scatter plots show samples drawn from both distributions, demonstrating the improved sampling efficiency of the tilted transport method.
More on tables

This table presents the results of a Gaussian mixture model experiment comparing the performance of Langevin dynamics and the proposed tilted transport method in posterior sampling. It showcases the sliced Wasserstein distance, a metric evaluating the similarity between the generated samples and the true posterior distribution. The table includes results for different dimensionality (d), and scenarios with reduced observation dimensions (d’=0.9d and d’=1). The results show that the tilted transport method consistently outperforms Langevin dynamics, especially when the observation dimensionality is significantly reduced.

This table presents the performance comparison between the DMPS method and the DMPS method boosted by tilted transport on four image processing tasks (denoising, inpainting, super-resolution, and deblurring) using the Flickr-Faces-HQ (FFHQ) dataset. The metrics used for comparison are Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index (SSIM), and Learned Perceptual Image Patch Similarity (LPIPS). Higher PSNR and SSIM values and lower LPIPS values indicate better image quality.
Full paper#



















