↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Stochastic combinatorial semi-bandits pose a significant challenge in online decision-making due to the exponentially large action space and complex reward structures. Existing algorithms often struggle to balance exploration and exploitation effectively, leading to suboptimal regret bounds. Furthermore, many existing algorithms are computationally expensive, hindering their applicability to real-world problems.
This work addresses these challenges by developing two novel algorithms. OLS-UCB-C, a deterministic algorithm, leverages online estimations of the covariance structure to achieve improved regret bounds. COS-V, a sampling-based algorithm inspired by Thompson Sampling, offers improved computational efficiency while still maintaining a near-optimal regret bound. Both algorithms provide gap-free regret bounds, showcasing their effectiveness across various problem sizes. The research highlights the practical benefits of adapting to the problem’s structure and the efficiency gains achievable through sampling methods.
Key Takeaways#
Why does it matter?#
This paper is important because it presents the first optimal gap-free regret upper bound for covariance-adaptive algorithms in stochastic combinatorial semi-bandits. It also introduces the first sampling-based algorithm achieving a O(√T) gap-free regret, significantly improving computational efficiency. This research bridges the gap between theoretical optimality and practical feasibility and opens avenues for further investigation in more complex bandit settings.
Visual Insights#
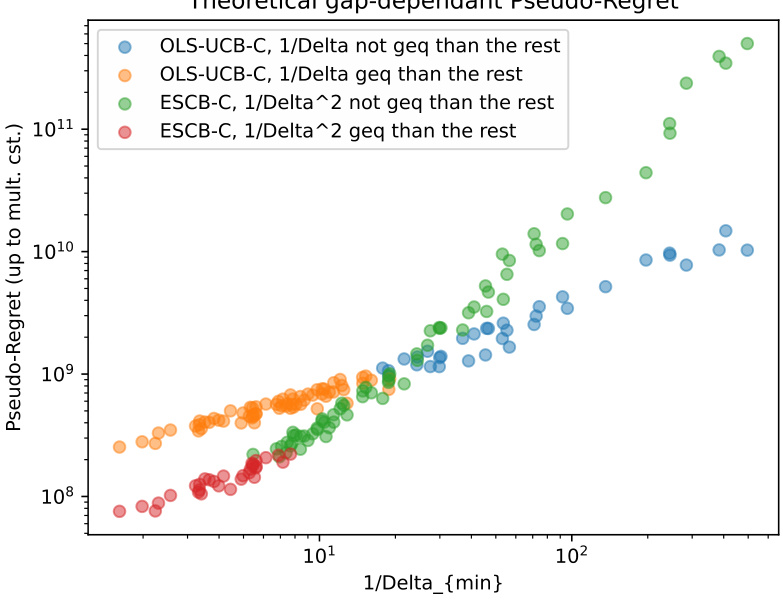
This figure shows the impact of the smallest suboptimality gap (Amin) on the theoretical gap-dependent regret upper bounds for ESCB-C and OLS-UCB-C algorithms. The x-axis represents 1/Amin, and the y-axis shows the pseudo-regret (up to a multiplicative constant). Different colors represent different scenarios, where the main term of the upper bound (1/Amin or 1/Amin²) is either greater than or less than the remaining terms. The figure aims to show how the theoretical regret changes with Amin. It reveals that OLS-UCB-C outperforms ESCB-C when Amin is very small, but ESCB-C can be better when Amin is relatively larger.

The table compares the asymptotic regret bounds and per-round time complexities of several deterministic and stochastic algorithms for combinatorial semi-bandits. It shows how different algorithms leverage information from the semi-bandit feedback (semi-bandit feedback) and/or knowledge of the covariance structure (covariance-adaptive), affecting both the regret and the computational cost. The algorithms are categorized by feedback type (bandit or semi-bandit) and algorithm type (deterministic or stochastic). For each algorithm, regret bounds (gap-free and gap-dependent) and time complexity are shown, providing a comprehensive overview of state-of-the-art methods.
In-depth insights#
Regret Bound Analysis#
Regret bound analysis in online learning algorithms, particularly in the context of combinatorial semi-bandits, focuses on quantifying the performance of algorithms over time. A key metric is the cumulative regret, representing the difference between the rewards obtained by an optimal strategy and the algorithm’s actual rewards. Regret bounds provide theoretical guarantees, typically upper bounds, on the expected cumulative regret. A tight regret bound is crucial; it assures the algorithm’s performance within a specified limit, usually scaling with the square root of the time horizon. The analysis often involves intricate probabilistic arguments, leveraging concentration inequalities to handle stochasticity in the reward process. Gap-free bounds, which hold even without assuming a gap between the optimal and suboptimal actions, are particularly desirable. Covariance-adaptive bounds demonstrate improved efficiency by accounting for dependencies between item rewards. Such analyses are key to understanding the algorithm’s efficacy and its suitability for practical applications, especially when computational complexity of the algorithm is a major consideration.
Algo. Optimality#
Analyzing algorithm optimality requires a multifaceted approach. Theoretical guarantees, often expressed as regret bounds, provide a crucial benchmark, indicating how an algorithm’s performance scales with the problem size and time horizon. However, tight bounds are not always achievable, and the practical performance might deviate. Computational complexity is another critical aspect; an algorithm’s theoretical superiority becomes irrelevant if it is computationally intractable for real-world problems. Empirical evaluations, through simulations or real-world datasets, are essential for validating theoretical claims and understanding the algorithm’s behavior in practical scenarios. Adaptive algorithms, which adjust their behavior based on observed data, are particularly interesting since they can potentially achieve better optimality and efficiency than static algorithms. Ultimately, a complete understanding of algorithm optimality necessitates a synergy between rigorous theoretical analysis and robust empirical verification. The choice of performance metric (e.g., regret, accuracy, runtime) also significantly influences the optimality assessment, emphasizing the need for a problem-specific analysis.
Sampling-Based Algo#
Sampling-based algorithms, particularly in the context of combinatorial semi-bandits, offer a compelling alternative to deterministic approaches. Their inherent randomness allows for efficient exploration of the vast action space, often outperforming deterministic methods in scenarios with exponentially many actions. Thompson Sampling is a prominent example, leveraging probabilistic models of the reward distribution to guide action selection. However, analyzing the regret of sampling-based algorithms can be significantly more challenging than for deterministic counterparts. This often results in looser regret bounds or the need for strong assumptions on the reward structure. Key advantages often include reduced computational complexity compared to solving complex optimization problems inherent in many deterministic strategies. This is especially beneficial in large-scale applications. Despite the analytical difficulties, the potential for improved efficiency and scalability makes sampling-based methods an important area of research for combinatorial semi-bandits. Future work may focus on developing novel sampling strategies and tighter regret analysis techniques that fully leverage the benefits of this approach.
Covariance Adaptation#
Covariance adaptation in machine learning, particularly within the context of bandit algorithms, involves dynamically adjusting strategies based on the estimated covariance structure of the reward distribution. Instead of assuming independence between different aspects of the reward (as in simpler bandit models), covariance-adaptive methods directly incorporate the relationships between rewards, leading to more efficient exploration and exploitation. This is crucial in settings with complex reward structures or dependencies, as it allows algorithms to focus on the most informative actions. Accurate estimation of the covariance matrix is a key challenge, requiring robust online estimation techniques to avoid overfitting or bias. Optimistic algorithms, which leverage confidence bounds derived from the covariance estimates, are often employed to balance exploration and exploitation effectively. The resulting performance improvements are particularly noticeable in high-dimensional settings or when dealing with structured action spaces, where ignoring the covariance structure leads to suboptimal results. Computational complexity is another significant factor, and some sampling-based approaches offer efficiency tradeoffs when the action space is extremely large.
Future Research#
Future research directions stemming from this work could explore several promising avenues. Extending the algorithms to handle more complex reward structures beyond linear models is crucial for broader applicability. Developing tighter theoretical bounds that account for the interplay between covariance and suboptimality gaps could lead to more refined regret analyses. Investigating the effectiveness of the proposed algorithms in high-dimensional settings or those with significant data sparsity would further demonstrate their practical potential. Combining the sampling-based and deterministic approaches might offer a hybrid method that balances computational efficiency with strong theoretical guarantees. Finally, empirical evaluation on diverse real-world problems with comprehensive comparisons to state-of-the-art methods would solidify the practical impact and identify areas needing further improvement.
More visual insights#
More on figures

This figure compares the performance of two algorithms, ESCB-C and OLS-UCB-C, in terms of pseudo-regret on randomly sampled environments. The x-axis represents the round number (log scale), and the y-axis shows the pseudo-regret (log scale). The plot includes the average pseudo-regret for both algorithms, along with confidence intervals (q25 and q75) to illustrate the variability in their performance. The shaded areas represent the confidence intervals.

The figure shows the final pseudo-regret of ESCB-C and OLS-UCB-C with respect to 1/Amin. Overall ESCB-C outperforms OLS-UCB-C, except in some corner cases. For cases with the smallest suboptimality gap, OLS-UCB-C outperforms ESCB-C.

This figure shows the pseudo-regret for both ESCB-C and OLS-UCB-C algorithms in the worst case scenario. While ESCB-C initially performs slightly better, it shows a sharp increase in pseudo-regret towards the end of the time horizon (105 rounds). This suggests that the approximation used in ESCB-C or the impact of its 1/Δmin term may cause a substantial increase in regret in certain scenarios. OLS-UCB-C exhibits smoother growth and appears more stable in this worst-case environment.
More on tables

This table compares the asymptotic regret bounds and time complexities of several algorithms for solving the stochastic combinatorial semi-bandit problem. It includes both deterministic and stochastic algorithms, highlighting their information requirements, computational costs, and regret performance in terms of gap-free asymptotic regret. The table categorizes algorithms based on feedback type (bandit or semi-bandit) and includes notations to clarify the symbols used in the regret bounds.

This table compares the asymptotic regret bounds and per-round time complexities of several combinatorial semi-bandit algorithms. It shows both deterministic and stochastic approaches, highlighting the gap-free and gap-dependent regret bounds achieved by each algorithm. The table also details the information used by each algorithm (e.g., covariance matrix or variance proxy) and its computational complexity. The algorithms are categorized by feedback type (bandit or semi-bandit).
Full paper#



















