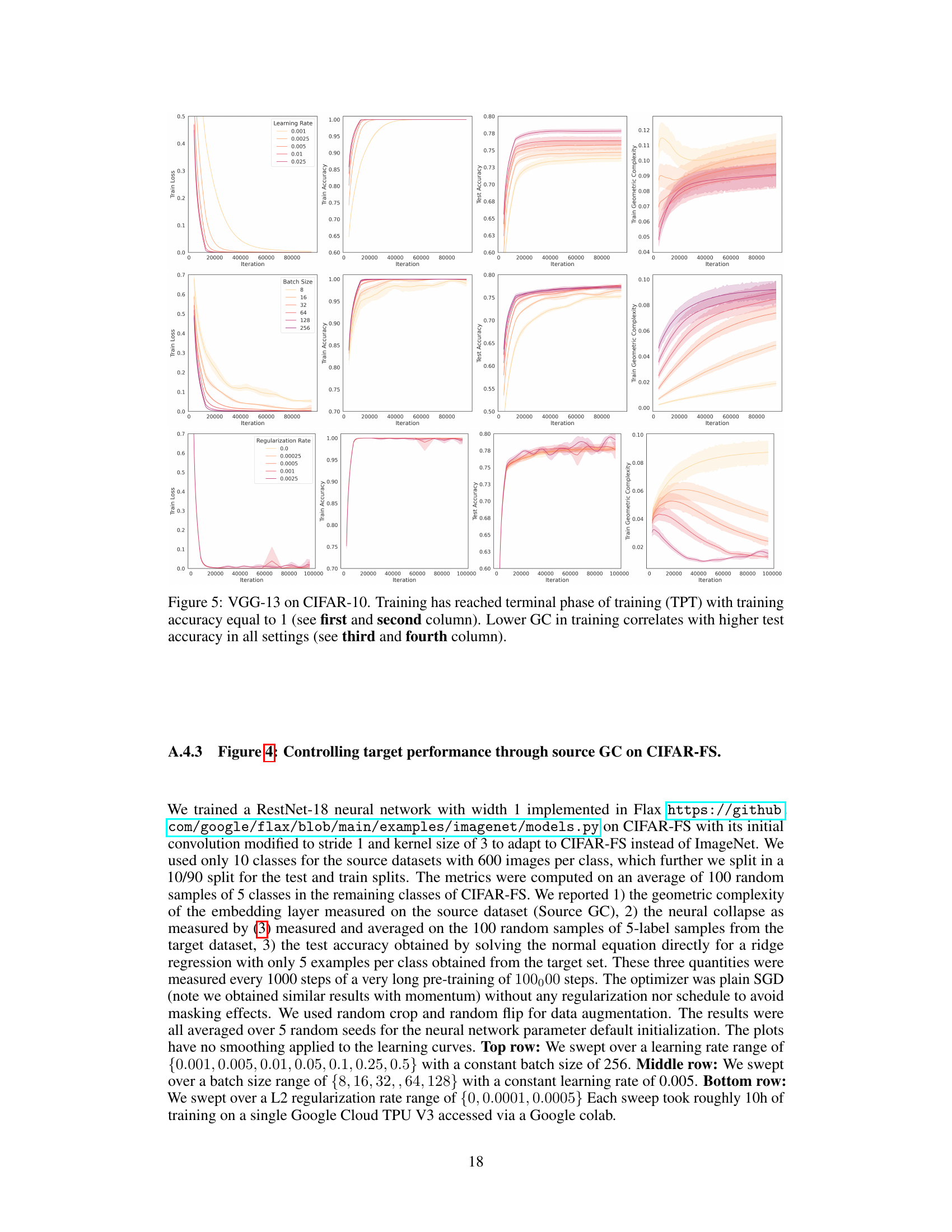
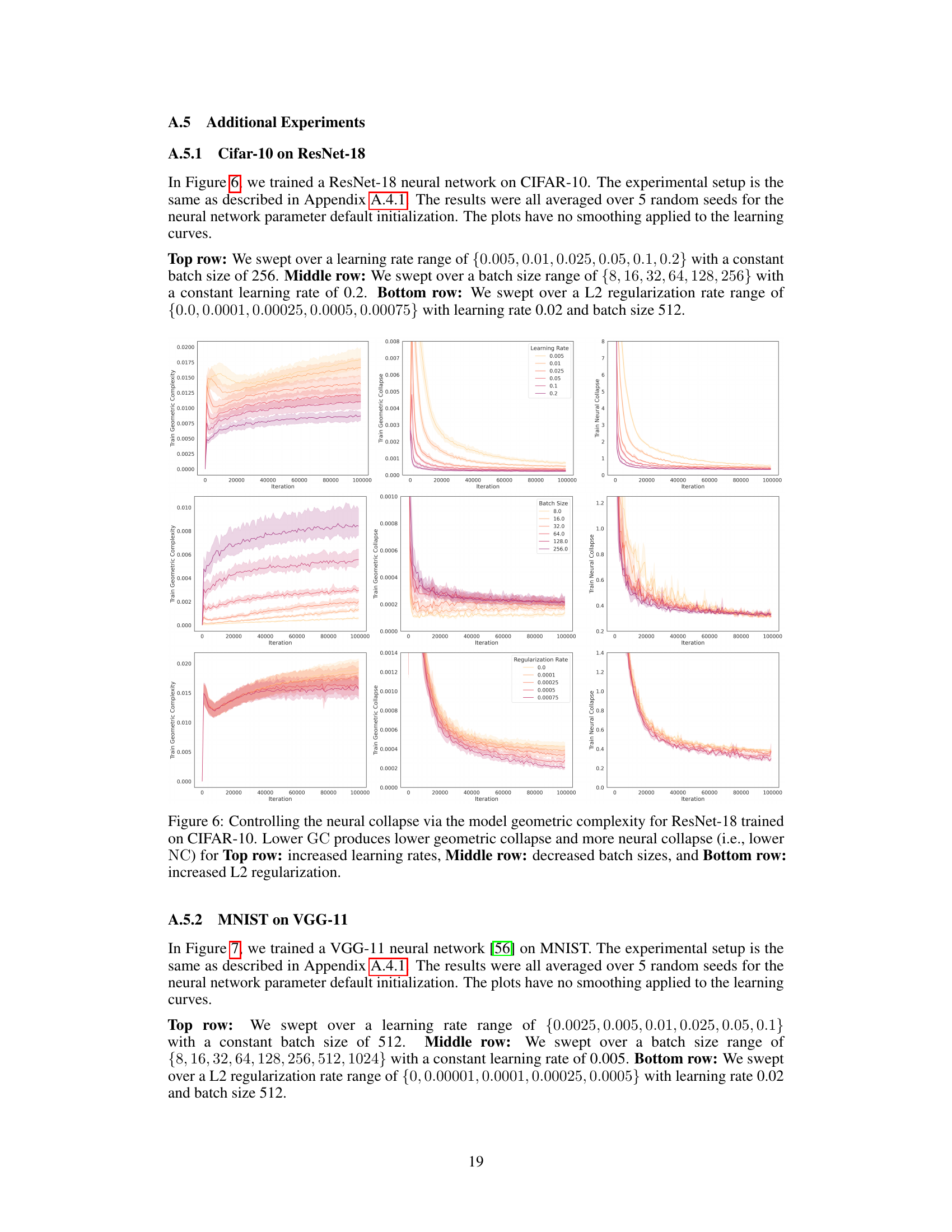
↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Transfer learning’s success in computer vision and language models remains incompletely understood. While metrics like loss surface flatness and neural collapse offer insights, a theoretical framework explaining them is lacking. A significant challenge lies in understanding how pre-training impacts the generalization of models to new, unseen tasks, especially with limited data. This paper addresses these issues by focusing on the implicit biases of deep neural networks.
This work proposes geometric complexity (GC) as a fundamental mechanism linking these concepts. Through experiments and theory, the authors demonstrate that controlling GC during pre-training directly influences neural collapse on both source and target tasks. They introduce GC as a new progress metric for transfer learning, offering a computationally tractable alternative to existing approaches. The resulting generalization bound shows improved transfer learning accuracy, particularly with fewer examples for downstream tasks. This novel perspective provides a unifying theoretical framework for understanding implicit biases in transfer learning.
Key Takeaways#
Why does it matter?#
This paper is crucial because it bridges the gap between empirical success and theoretical understanding of transfer learning. It introduces geometric complexity as a key factor influencing neural collapse, offering new progress metrics and a theoretical framework for improving transfer learning performance, particularly in low-data settings. This opens avenues for designing better pre-training strategies and optimizing downstream task performance.
Visual Insights#
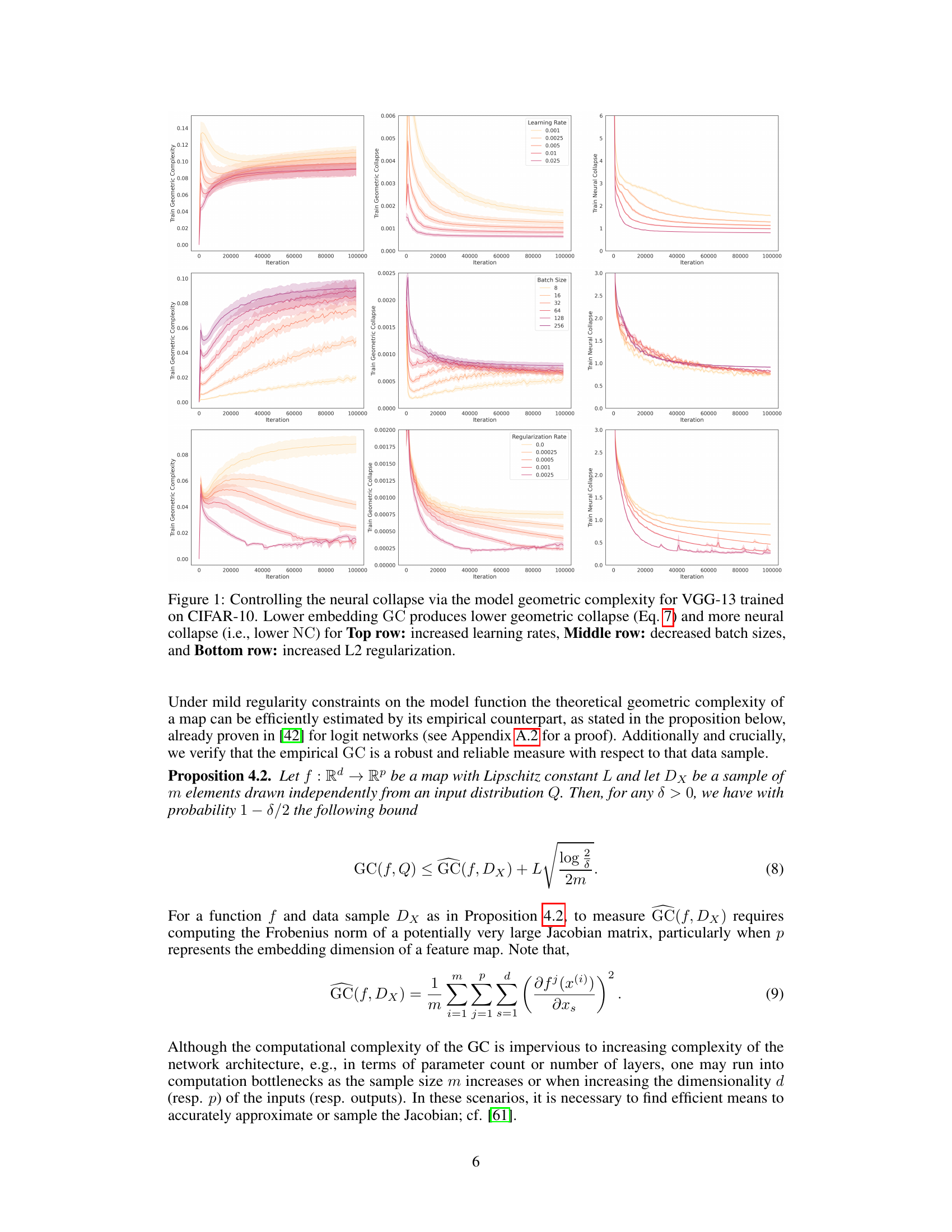
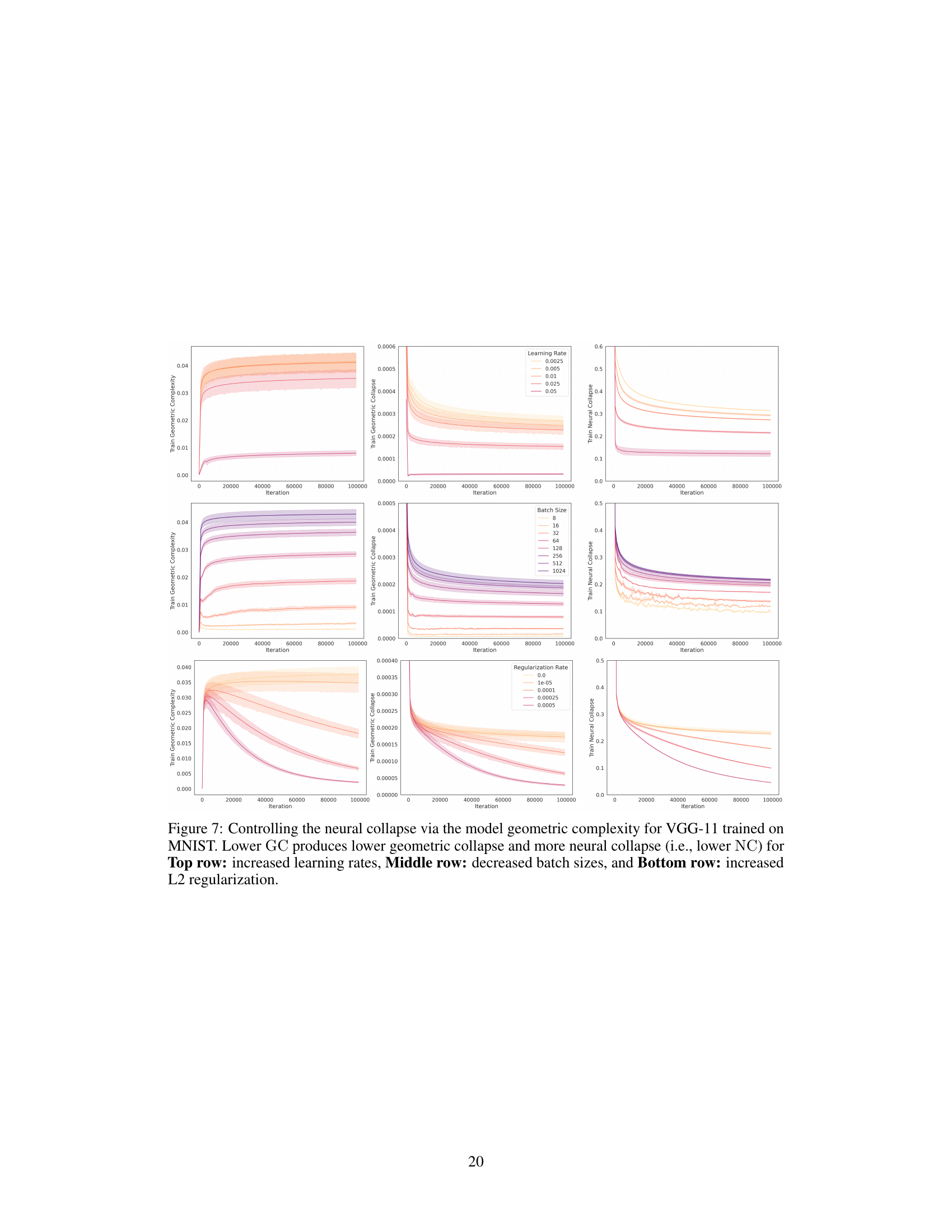
This figure shows the impact of different hyperparameters on the relationship between geometric complexity (GC) and neural collapse (NC) in a VGG-13 model trained on CIFAR-10. Three sets of experiments are presented, each varying a different hyperparameter: * Learning Rate: Shows that higher learning rates lead to higher GC and less neural collapse. * Batch Size: Demonstrates that smaller batch sizes result in lower GC and more neural collapse. * L2 Regularization: Illustrates how stronger L2 regularization reduces GC and enhances neural collapse. The results support the paper’s claim that lower GC promotes better neural collapse, improving downstream task performance.
In-depth insights#
Geometric Collapse#
Geometric collapse, a phenomenon observed in deep learning, describes the tendency of learned feature representations to cluster around their respective class means during the training process. This clustering forms a regular geometric structure, often an equiangular tight frame, significantly improving generalization. The paper explores the connection between geometric collapse and other implicit biases, specifically geometric complexity of the learned features. Geometric complexity (GC) quantifies the variability of a function. Lower GC encourages neural collapse, implying that simpler, less variable functions are favored by the training process. This offers a novel theoretical framework for understanding transfer learning, where pre-trained models with low GC and resulting neural collapse generalize better to new tasks, particularly in low-data scenarios. The empirical estimation of GC’s computational efficiency and robustness make it a promising hidden metric for assessing transfer learning progress.
Transfer Learning#
The concept of transfer learning is central to the research paper, focusing on how pre-trained models, developed on large-scale datasets, can be effectively adapted for new, often smaller, downstream tasks. The paper investigates the underlying mechanisms driving the success of transfer learning, moving beyond empirical observations to explore the role of implicit biases. A key focus is the relationship between a model’s geometric complexity and its performance in the few-shot learning setting. The authors hypothesize that models with lower geometric complexity during pre-training exhibit better transferability, as lower complexity often leads to improved neural collapse on target tasks. This is further supported by theoretical analysis and generalization bounds. The research presents a novel theoretical framework connecting various concepts such as flatness of loss surfaces, geometric complexity, and neural collapse to better understand how implicit biases govern the process of transfer learning. Ultimately, the paper aims to provide a deeper understanding of the mechanisms governing transfer learning and to develop improved metrics for evaluating the transferability of pre-trained models.
GC Impact#
The concept of ‘GC Impact’, likely referring to the impact of Geometric Complexity (GC) on model performance, is a central theme. The research suggests a strong negative correlation between GC and downstream task performance, especially in few-shot learning scenarios. Lower GC, achieved through various implicit regularization mechanisms, leads to better generalization and improved neural collapse. This indicates that simpler, less variable functions learned during pre-training translate to more effective transfer learning, where the model readily adapts to new, unseen data. The theoretical framework developed supports the empirical findings, emphasizing the role of GC as a crucial factor in understanding the implicit biases driving successful transfer learning. Further research is needed to fully explore the implications of GC across diverse models and datasets.
GC Regularization#
The concept of ‘GC Regularization’ within the context of deep learning and neural networks is an intriguing one. It suggests a method of regularizing the model’s complexity by directly controlling its geometric complexity (GC). Lower GC values, empirically observed in the paper, correlate with improved generalization and better transfer learning performance. This is achieved by implicitly or explicitly applying pressure on the learning dynamics to favor solutions with smoother functions and simpler geometric structures in the embedding space. This approach elegantly ties together various implicit biases in deep learning, such as loss surface flatness and neural collapse, into a unified framework. It allows one to control generalization by carefully balancing the trade-off between model fit and model complexity, directly addressing the issue of overfitting. The effectiveness of GC regularization is further underscored by the paper’s theoretical generalization bounds and its empirical validation on various datasets and architectures. The computational efficiency of GC estimation presents a significant practical advantage, enabling its deployment in diverse scenarios.
Future Work#
Future research could explore extending the geometric complexity framework to other domains like natural language processing, where the notion of neural collapse requires further investigation. Exploring alternative ways to regularize geometric complexity, beyond the methods presented, such as using different loss functions or network architectures, is also warranted. A more in-depth analysis of the relationship between geometric complexity and other implicit biases, such as those related to loss surface flatness and learning path sharpness, could yield a more comprehensive understanding of deep learning generalization. Furthermore, studying the effects of data distribution characteristics on geometric complexity and its impact on transfer learning is crucial. Finally, developing efficient methods for approximating geometric complexity in high-dimensional settings is needed to improve computational efficiency and broaden its applicability.
More visual insights#
More on figures
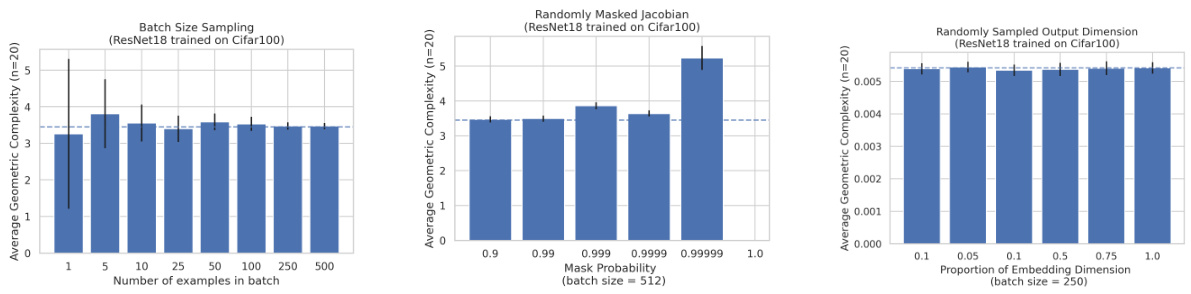
This figure demonstrates the robustness and reliability of the geometric complexity (GC) measure when computed using different sampling methods. Three scenarios are tested: sampling by batch size (number of examples), sampling by masking portions of the Jacobian matrix, and sampling by randomly selecting output dimensions. The results show that even with these sampling techniques, the empirical GC remains consistent with the true GC, indicating its computational efficiency and reliability as a complexity measure.
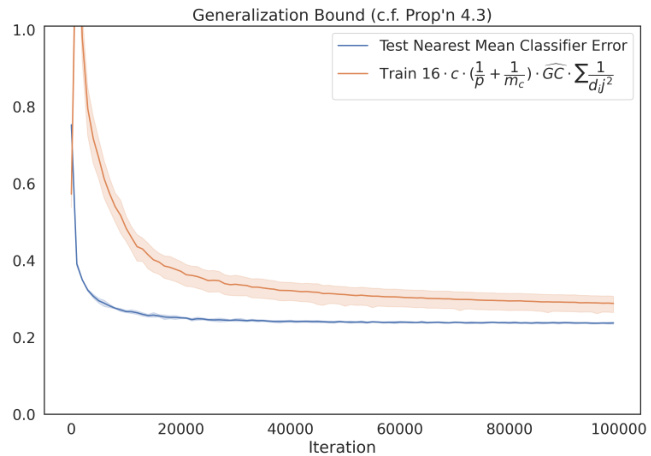
This figure shows the relationship between the geometric complexity and the test error of a VGG-13 model trained on CIFAR-10. The x-axis represents the number of iterations during training, and the y-axis represents the generalization bound (LHS) and the test error of the nearest-mean classifier (RHS). The plot demonstrates that the generalization bound is not vacuous and provides a relatively tight fit, indicating the effectiveness of the geometric complexity in bounding the generalization error. The figure also displays the results from 5 separate training runs with different random seeds, showcasing the robustness of the relationship between geometric complexity and generalization performance.
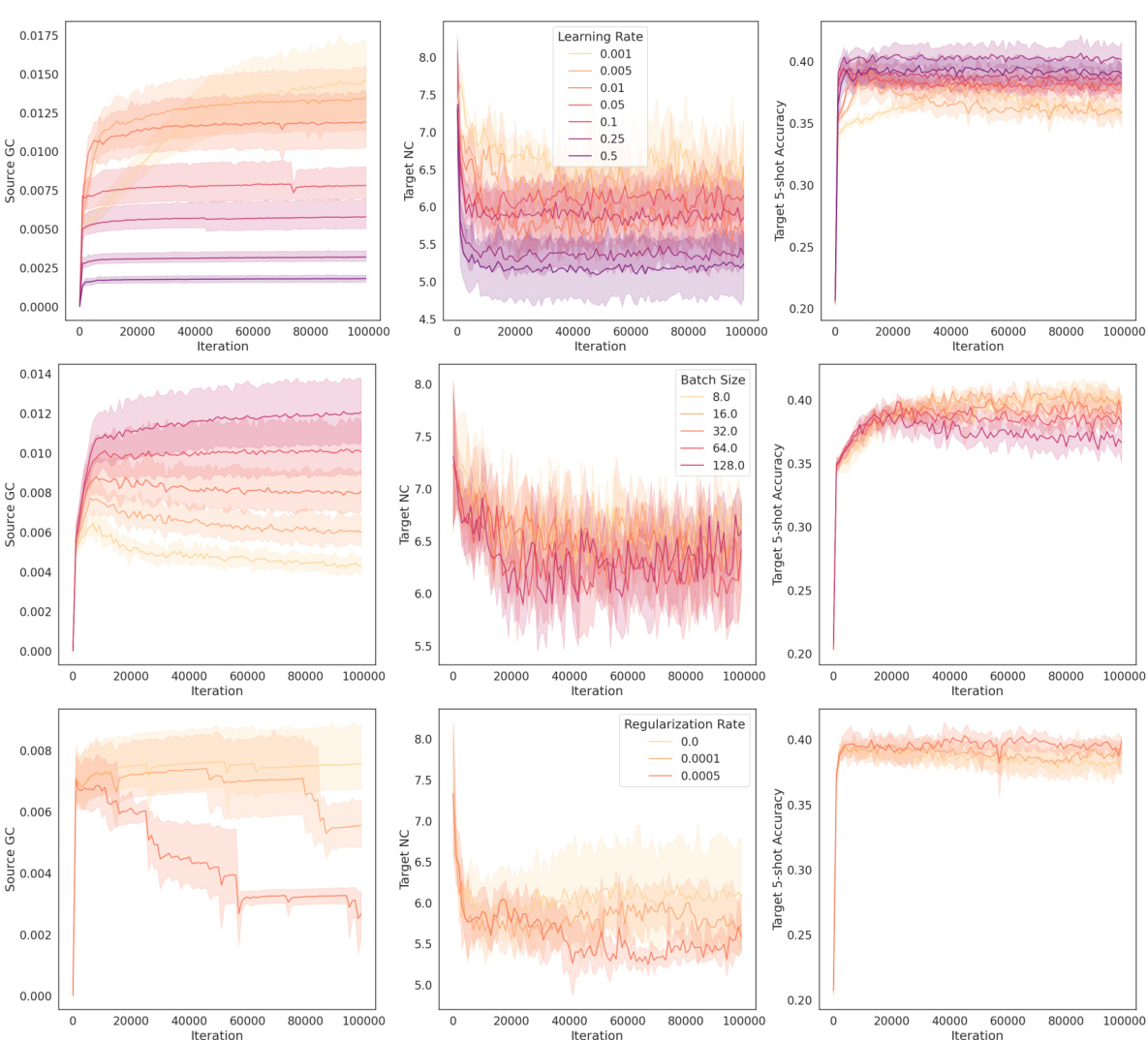
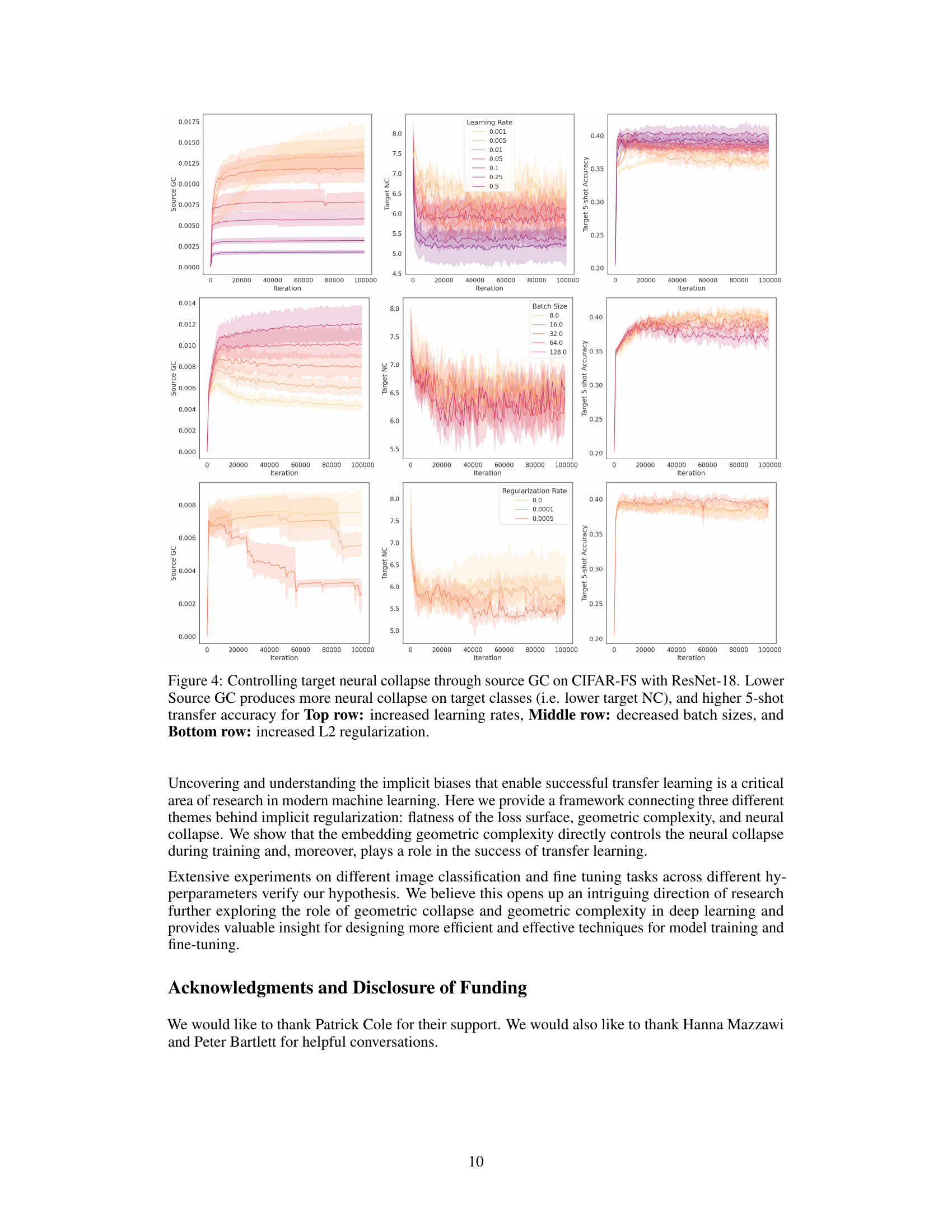
This figure shows the results of experiments on CIFAR-FS using ResNet-18, demonstrating the relationship between source geometric complexity (GC), target neural collapse (NC), and 5-shot transfer accuracy. Three sets of experiments are presented, each manipulating a different hyperparameter: learning rate, batch size, and L2 regularization. The results consistently show that lower source GC leads to lower target NC and improved 5-shot accuracy.
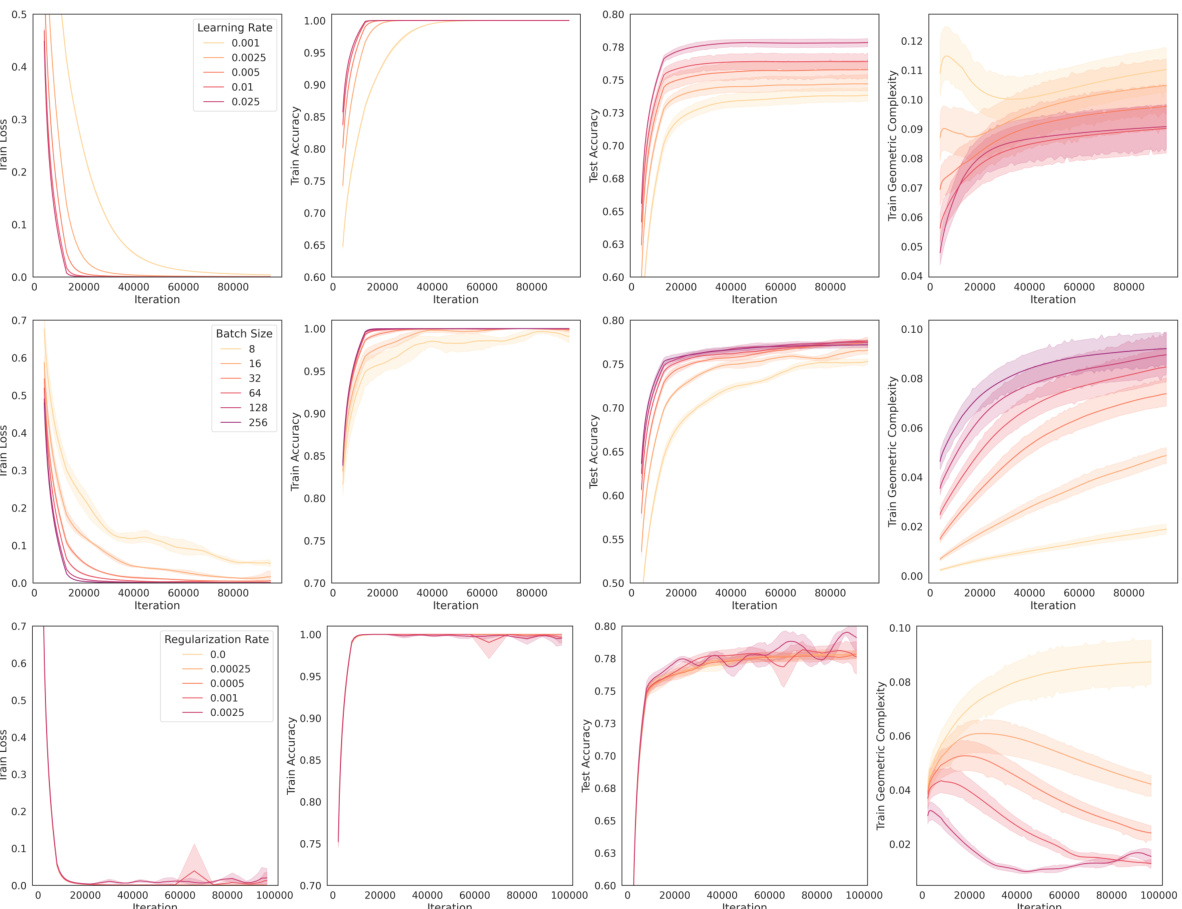
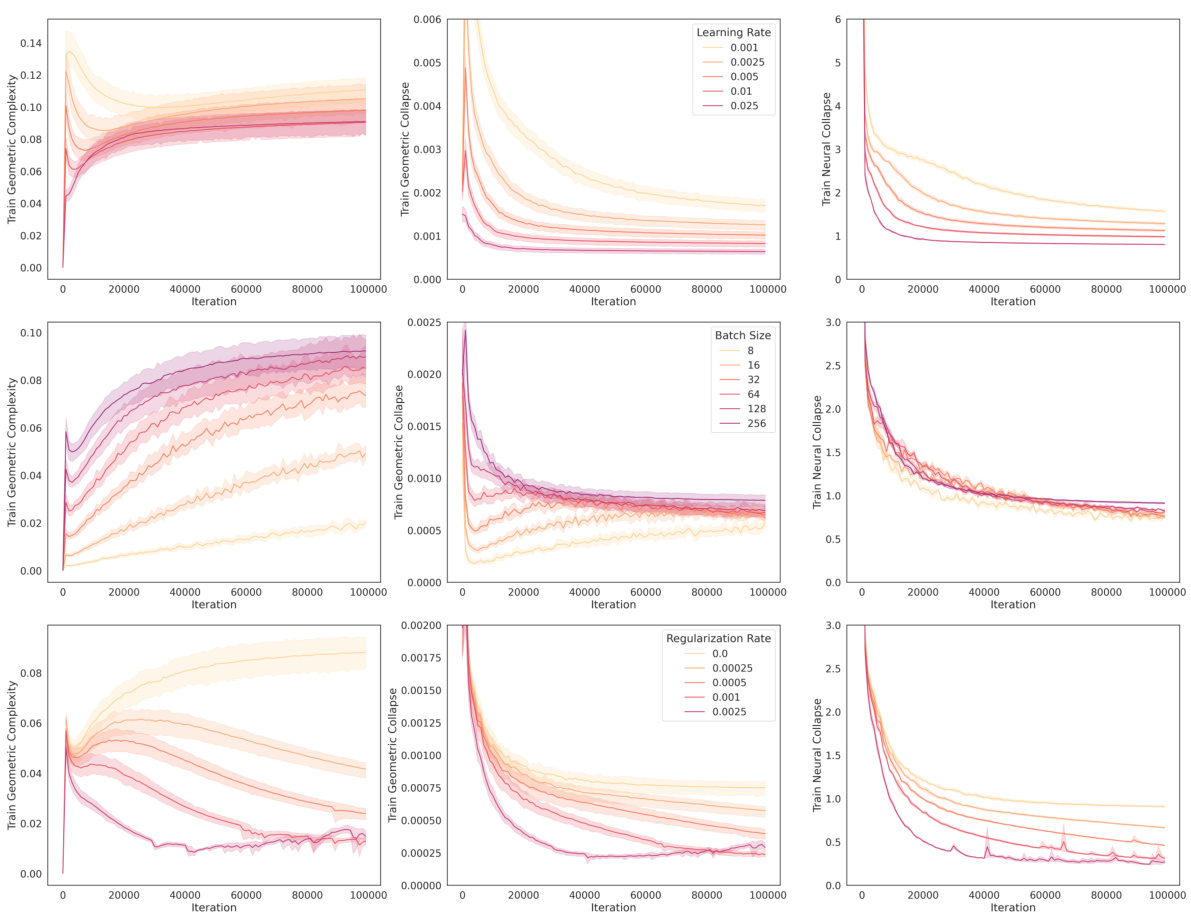
This figure demonstrates the relationship between geometric complexity and neural collapse in a VGG-13 model trained on CIFAR-10. It shows how manipulating training hyperparameters (learning rate, batch size, L2 regularization) affects the geometric complexity (GC) and neural collapse (NC). Lower GC correlates with lower geometric collapse and higher neural collapse, indicating that controlling GC is a way to influence the neural collapse phenomenon and potentially improve model performance.

This figure shows how controlling the geometric complexity of a VGG-13 model trained on CIFAR-10 affects neural collapse. Three sets of experiments are presented, each varying a different hyperparameter: learning rate, batch size, and L2 regularization. The results demonstrate that lower geometric complexity leads to lower geometric collapse and more pronounced neural collapse. This highlights the relationship between geometric complexity and neural collapse.
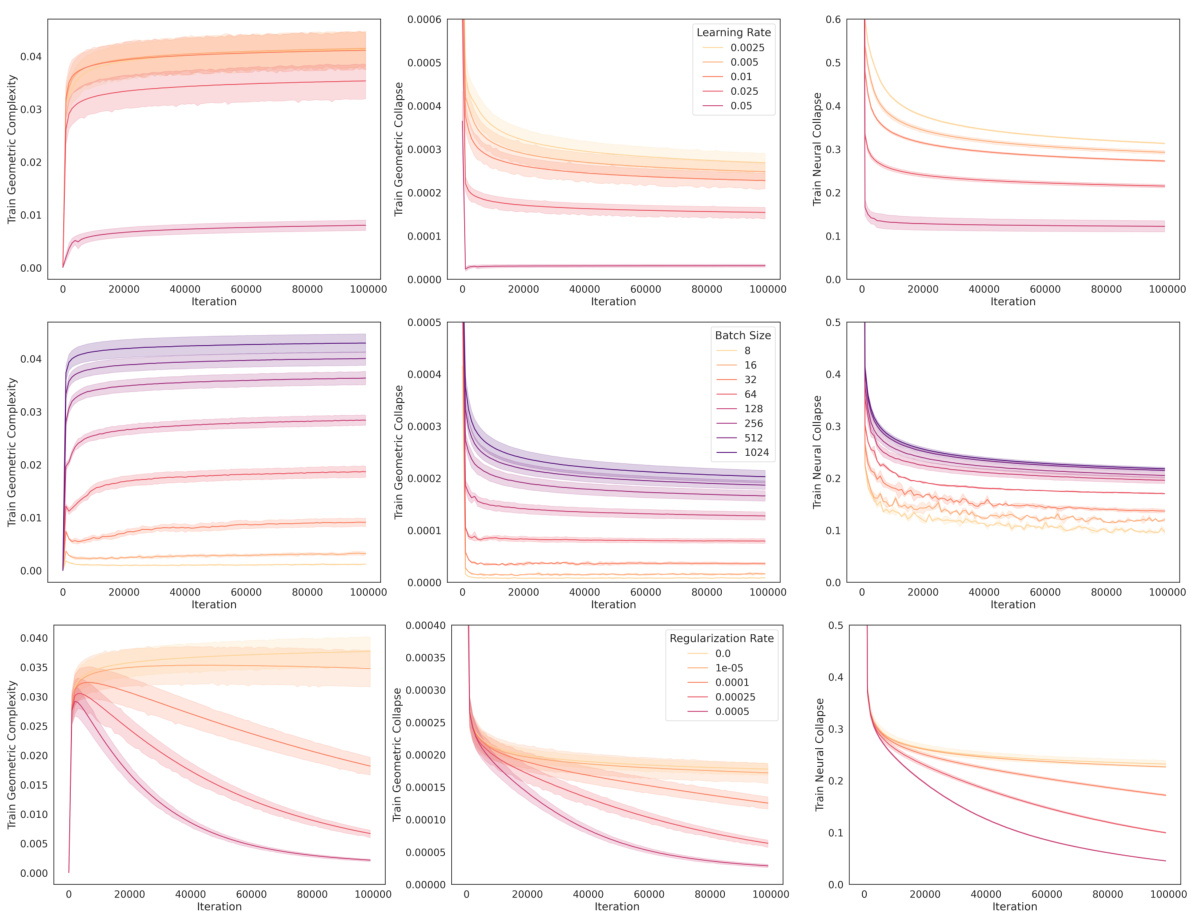
This figure shows the effects of different hyperparameters (learning rate, batch size, L2 regularization) on the geometric complexity, geometric collapse, and neural collapse during the training of a VGG-11 neural network on the MNIST dataset. The results demonstrate that lower geometric complexity (GC), achieved through various regularization techniques, leads to lower geometric collapse and increased neural collapse (i.e., lower NC values, indicating better class separation in the embedding space). This suggests that controlling geometric complexity can be a useful way to influence the final performance of a model.
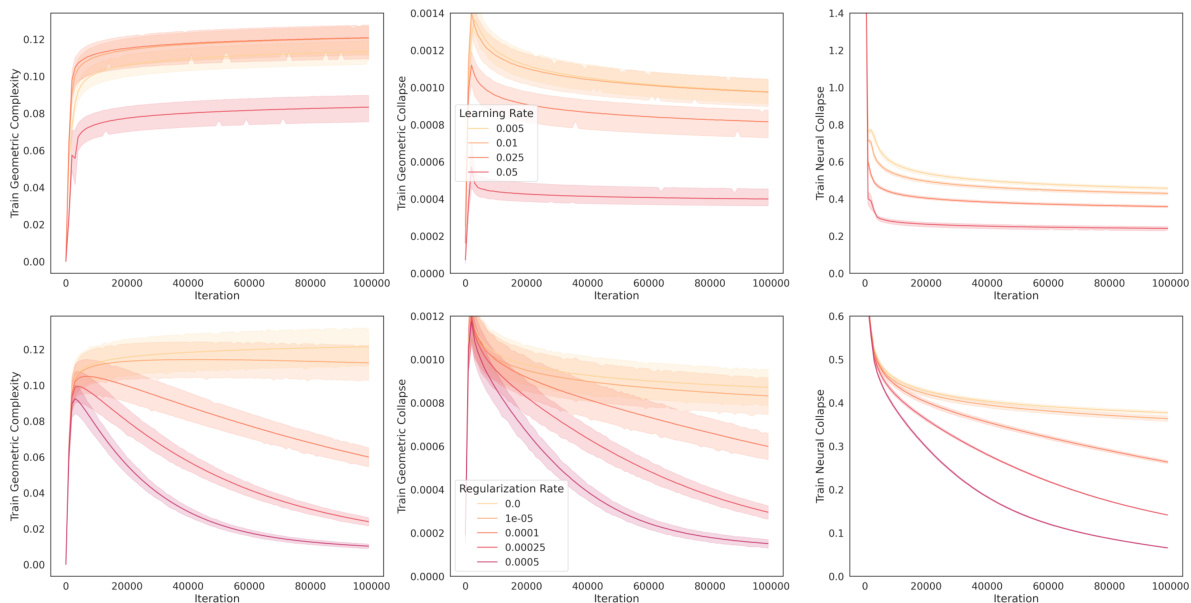
This figure shows the relationship between geometric complexity and neural collapse during the training of a VGG-13 network on the CIFAR-10 dataset. It demonstrates how manipulating training hyperparameters (learning rate, batch size, and L2 regularization) affects the geometric complexity and, consequently, the neural collapse. Lower geometric complexity is associated with increased neural collapse, as indicated by the lower CDNV values. The figure presents results across various settings, showing a consistent trend of lower geometric complexity leading to increased neural collapse and potentially improved generalization.

This figure shows how the geometric complexity (GC) of a VGG-13 model, trained on CIFAR-10, affects neural collapse (NC). The plots demonstrate that lower embedding GC leads to lower geometric collapse and increased NC. This effect is shown across three different scenarios: varying learning rates, batch sizes, and L2 regularization. Each row represents one of these scenarios, illustrating the consistent relationship between GC and NC under different training conditions.
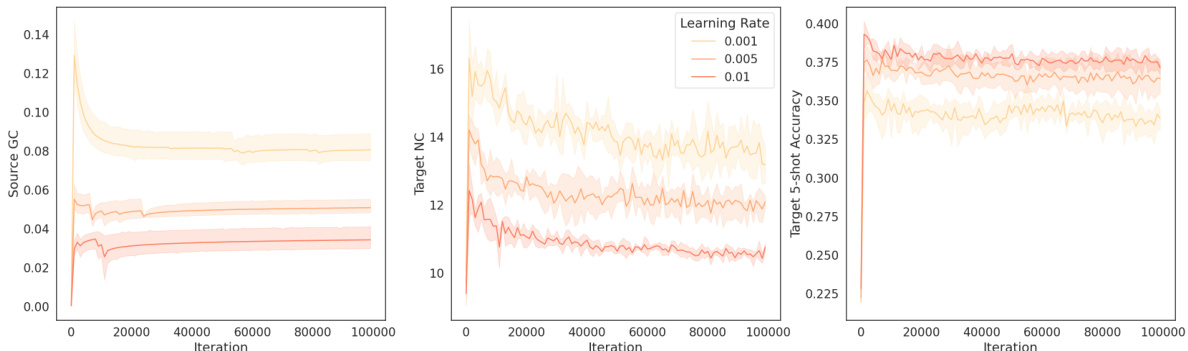
This figure shows the results of an experiment where the researchers investigated the effect of source geometric complexity (GC) on target neural collapse and transfer learning performance. Using a ResNet-18 model on the CIFAR-FS dataset, they manipulated three factors: learning rate, batch size, and L2 regularization, observing their effects on both source GC (during pre-training) and target neural collapse (during fine-tuning). The plots illustrate that lower source GC correlates with lower target neural collapse, leading to better 5-shot accuracy on the target task.

This figure shows the results of training a VGG-13 model on CIFAR-10 dataset with explicit geometric complexity (GC) regularization. The experiment uses a fixed learning rate of 0.01 and a batch size of 256. Different levels of GC regularization (1e-07, 1e-06, 0.0001) are applied. The figure presents the training curves for three metrics: Train Geometric Complexity, Train Geometric Collapse, and Train Neural Collapse. It demonstrates that increasing the amount of GC regularization leads to lower values for these three metrics.
Full paper#