TL;DR#
Optimization over permutations is an NP-hard problem frequently encountered in machine learning tasks like ranking and matching. Existing methods often involve relaxations onto the Birkhoff polytope, but these can have limitations in terms of dimensionality and the preservation of geometric structures. The Birkhoff polytope-based methods also often require penalty terms to encourage solutions that are near permutation matrices.
This paper introduces OT4P, a novel approach that relaxes permutations onto the orthogonal group. OT4P uses a temperature-controlled differentiable transformation to map an unconstrained vector space to the orthogonal group, concentrating the orthogonal matrices near the permutation matrices. This provides a more efficient parameterization than the Birkhoff polytope and avoids the need for penalty terms. The paper shows how to use this parameterization for both gradient-based and stochastic optimization and demonstrates its efficacy on several benchmark problems. The results demonstrate improved performance in terms of accuracy and efficiency.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel and efficient method for addressing the NP-hard problem of optimization over permutations, a challenge faced in various machine learning tasks. OT4P offers unique advantages over existing methods by leveraging the orthogonal group, leading to potentially improved efficiency and scalability. This opens avenues for advancing research in areas such as ranking, matching, and tracking. The proposed method’s flexibility and simplicity could also make it a valuable tool for a wider range of researchers.
Visual Insights#

🔼 This figure illustrates the two-step process of the OT4P transformation. Step I shows how an unconstrained vector from Rn(n-1)/2 is mapped to an orthogonal matrix in SO(n) using the Lie exponential map. Step II demonstrates the temperature-controlled geodesic movement from the orthogonal matrix towards the closest permutation matrix in the manifold Mp. The colored dots visualize the transformation process, emphasizing the convergence of orthogonal matrices to permutation matrices as the temperature approaches its limit.
read the caption
Figure 1: Illustration of OT4P with colored dots to help visualize the transformation. In the limit of temperature, the orthogonal matrices obtained from OT4P converge near the permutation matrices.

🔼 This table presents the results of comparing three different algorithms (Weight Matching, Sinkhorn, and OT4P with three different temperatures) for finding mode connectivity across three different network architectures (MLP5, VGG11, and ResNet18). The metrics used for comparison are the l1-distance (after a log(1+x) transformation) and the precision. Lower l1-distance indicates better performance, while higher precision indicates a more accurate identification of the optimal permutation.
read the caption
Table 1: l1-Distance (converted by log(1 + x)) and Precision (%) of algorithms for finding mode connectivity across different network architectures.
In-depth insights#
OT4P: Perm Relaxation#
The heading “OT4P: Perm Relaxation” suggests a novel method, OT4P, for addressing permutation relaxation problems. This likely involves a technique that maps the discrete space of permutations into a continuous space, making optimization more tractable. The method’s name hints at the use of an orthogonal group, which is a continuous Lie group with useful geometric properties. This approach probably offers advantages such as lower dimensionality compared to other methods like Birkhoff polytope relaxations and the ability to preserve inner products. The “Perm Relaxation” part indicates that the method tackles the inherent difficulty in optimizing over the discrete set of permutation matrices, common in various applications like graph matching and ranking. The success of OT4P likely hinges on its ability to effectively approximate permutation matrices within the continuous orthogonal group, offering a balance between accuracy and computational efficiency. Differentiability is key for the algorithm to allow gradient-based optimization and the method possibly includes a temperature control parameter to adjust this tradeoff.
Orthogonal Group Path#
The concept of “Orthogonal Group Path” in the context of permutation relaxation presents a novel approach to address the computational challenges inherent in optimizing over permutation matrices. Instead of relying on relaxations within the Birkhoff polytope, it proposes a transformation that maps unconstrained vectors to the orthogonal group, a space with lower dimensionality and unique geometric properties. This transformation introduces flexibility by offering temperature control, allowing for smooth transitions between the orthogonal group and the set of permutation matrices. The effectiveness of this method lies in its ability to employ gradient-based optimization techniques, which are typically not directly applicable to discrete permutation problems. By exploiting the differentiable structure of the orthogonal group, stochastic optimization becomes feasible, opening doors for efficient probabilistic inference. This approach demonstrates a potentially significant improvement over existing Birkhoff polytope-based methods, particularly in terms of computational efficiency and the ability to handle probabilistic settings, but further research is needed to comprehensively assess its practical advantages and limitations.
Gradient-Based Optim.#
Gradient-based optimization is a cornerstone of modern machine learning, and its application to permutation problems is particularly insightful. The core idea revolves around relaxing the discrete nature of permutations, typically represented by permutation matrices, into a continuous space where gradient descent can be effectively applied. This relaxation often involves mapping the permutation problem onto a differentiable manifold, such as the Birkhoff polytope or the orthogonal group. The choice of manifold significantly impacts the optimization landscape, influencing both efficiency and the quality of the obtained solution. A key challenge lies in designing a suitable parameterization that maintains the inherent structure of the permutation problem while ensuring differentiability. The temperature-controlled differentiable transformation presented likely addresses this challenge by providing a flexible, parameter-free mechanism for gradually approaching the permutation matrix space. This approach likely avoids the need for penalty functions often employed in previous methods, thereby simplifying the optimization procedure and enhancing its stability. Ultimately, the success of this gradient-based approach hinges on the effectiveness of the chosen relaxation method and the careful design of the differentiable transformation. The effectiveness is empirically demonstrated through extensive experiments. The proposed method significantly enhances the performance in permutation problems compared to earlier work.
Stochastic Optimization#
Stochastic optimization addresses the challenge of optimizing functions where randomness is inherent. In the context of permutation problems, this often arises from the probabilistic nature of the underlying data or the need to model uncertainty. Standard gradient-based optimization methods are often insufficient due to the discrete and combinatorial nature of permutations. Stochastic optimization techniques, such as those employing re-parameterization tricks, offer a powerful approach by introducing randomness into the optimization process. This allows for gradient estimation through sampling and the efficient exploration of the vast permutation space, effectively navigating the non-convex landscape of the objective function. While deterministic methods often get stuck in local minima, the stochastic approach provides a better chance of escaping them and converging toward a global optimum. The choice of sampling scheme and the level of noise introduced are crucial parameters and require careful consideration. Overall, stochastic optimization is essential for handling permutation problems that involve uncertainty, providing flexibility and efficiency in the search for optimal solutions.
Limitations of OT4P#
OT4P, while effective, presents certain limitations. Computational cost increases significantly with larger matrices (n>1000) due to the eigendecomposition step, hindering scalability. The choice of noise distribution for stochastic optimization might not perfectly capture the latent permutation matrix variability, impacting performance. Boundary issues in representing permutation matrices, especially those with -1 eigenvalues, can hinder optimization and seamless integration into deep learning architectures. The temperature parameter (τ) requires careful tuning, as suboptimal choices might lead to poor performance. Finally, while OT4P offers advantages over Birkhoff polytope methods, the orthogonal group’s higher dimensionality than Birkhoff polytope could potentially lead to an enlarged search space, especially in high-dimensional problems. Addressing these limitations through efficient algorithms and alternative parameterizations warrants further investigation.
More visual insights#
More on figures
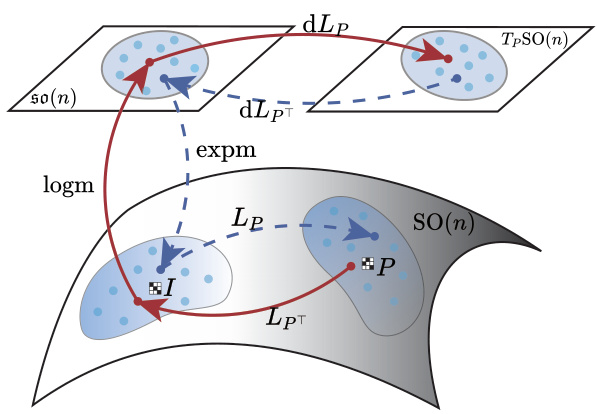
🔼 This figure illustrates the two mappings used in Step II of OT4P, which is the process of moving an orthogonal matrix O towards the closest permutation matrix P along a geodesic. The left translation Lp creates an isometry between the neighborhoods of the identity matrix I and P. Its derivative (dLp)e provides an isomorphism between the Lie algebra so(n) and the tangent space TpSO(n) at P. This isomorphism allows for efficient movement towards P in the tangent space, which is then mapped back to SO(n) using expmp. The entire process is designed to efficiently and accurately move O towards P using geodesic interpolation.
read the caption
Figure 2: Illustration of the mappings logmp and expmp. The left translation Lp establishes an isometry between the neighborhoods of I and P, and its derivative (dLp)e provides an isomorphism between so(n) and TpSO(n).

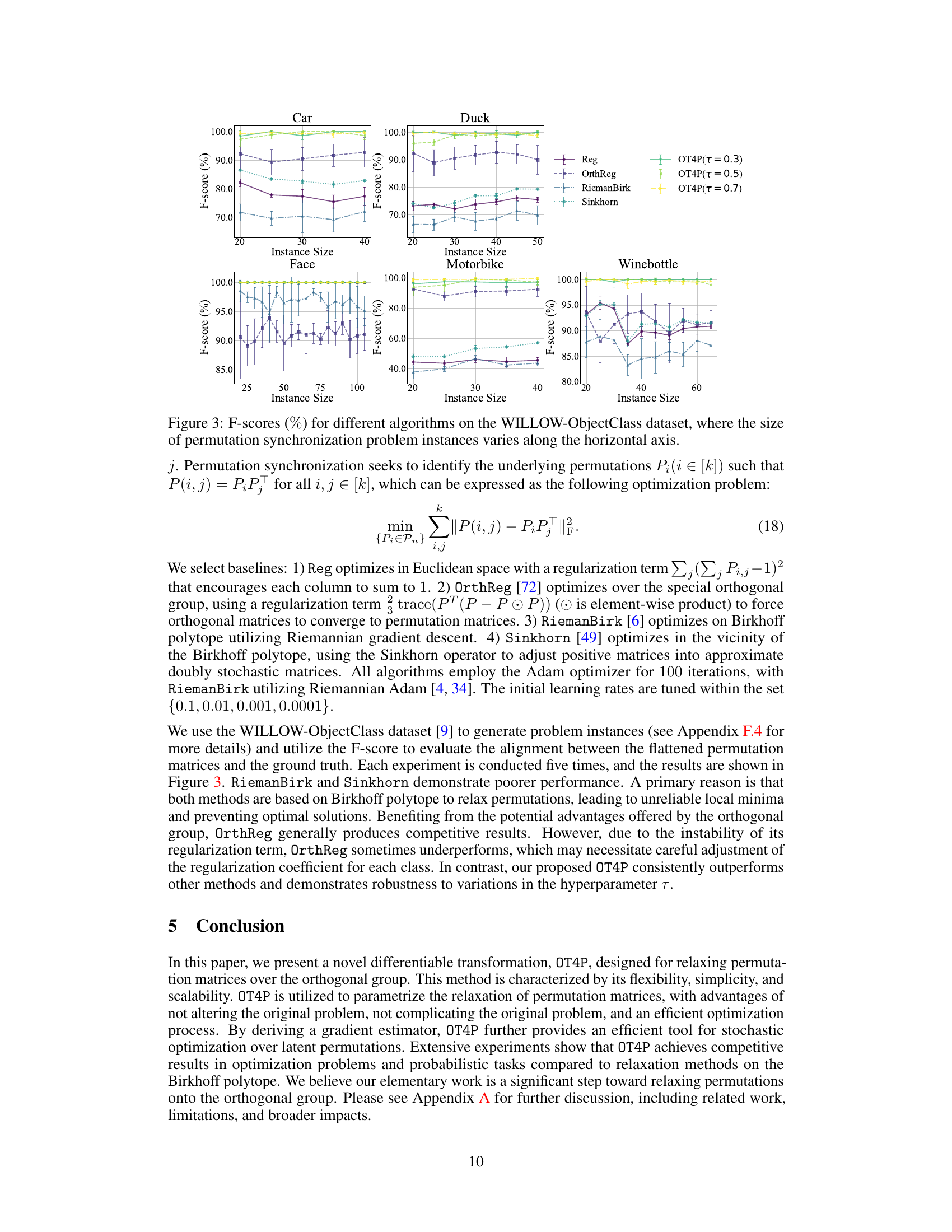
🔼 This figure compares the performance of different algorithms for solving permutation synchronization problems on the WILLOW-ObjectClass dataset. The x-axis represents the size of the problem instances, and the y-axis represents the F-score, a measure of the accuracy of the algorithms. The different lines represent different algorithms: Reg, OrthReg, RiemanBirk, Sinkhorn, and OT4P (with three different temperature parameters). The figure shows that OT4P generally outperforms the other algorithms, particularly as the problem size increases.
read the caption
Figure 3: F-scores (%) for different algorithms on the WILLOW-ObjectClass dataset, where the size of permutation synchronization problem instances varies along the horizontal axis.
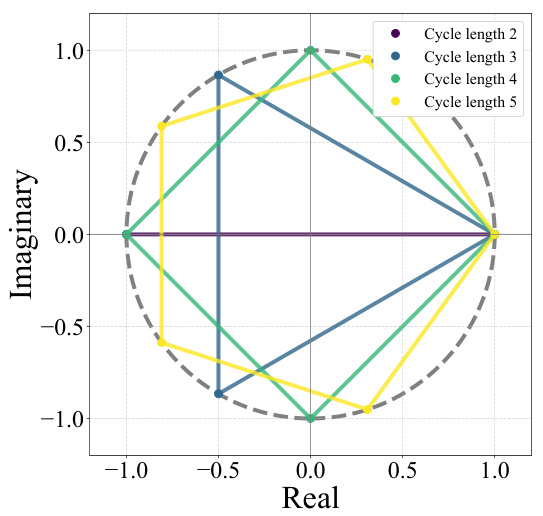
🔼 This figure visualizes the eigenvalues of permutation matrices corresponding to cycles of different lengths (2, 3, 4, and 5). It demonstrates that cycles of even length consistently have an eigenvalue of -1. Since the eigenvalues of a permutation matrix are composed of those from the submatrices corresponding to its contained cycles, this illustrates that many permutation matrices possess an eigenvalue of -1.
read the caption
Figure 4: Eigenvalues corresponding to cycles of different lengths, where eigenvalues from the same cycle are connected to illustrate repeated values at -1.

🔼 This figure visualizes how the transformation in Equation (11) affects orthogonal matrices as the temperature parameter τ changes. The top row shows the transformation for even permutations, while the bottom row shows it for odd permutations. As τ decreases from 1.0 to 0.0, the orthogonal matrices gradually approach their nearest permutation matrices. This demonstrates the temperature control mechanism of OT4P in mapping unconstrained vector spaces to orthogonal matrices, concentrating them near permutation matrices as temperature approaches 0.
read the caption
Figure 5: Visualization of the results of Equation (11) as the parameter τ varies. At τ = 1.0, the matrices are original orthogonal matrices; at τ = 0.0, they are the permutation matrices closest to original orthogonal matrices.

🔼 This figure compares the performance of different algorithms (Reg, OrthReg, RiemanBirk, Sinkhorn, and OT4P with different temperature parameters) on the WILLOW-ObjectClass dataset for the permutation synchronization problem. The x-axis represents the size of the problem instance (number of points to match), and the y-axis represents the F-score, a measure of the accuracy of the matching. The figure shows that OT4P consistently achieves higher F-scores than the other methods, particularly as the problem size increases. This demonstrates the effectiveness of OT4P for large-scale permutation synchronization problems.
read the caption
Figure 3: F-scores (%) for different algorithms on the WILLOW-ObjectClass dataset, where the size of permutation synchronization problem instances varies along the horizontal axis.

🔼 This figure visualizes the results of applying OT4P to the CMU House dataset with k=110. It shows the matching between the first and last images of the sequence. Green lines represent correctly matched points, while red lines indicate incorrect matches. Different subfigures show the results for different values of the temperature parameter τ, demonstrating how the accuracy of the matching changes with different τ values.
read the caption
Figure 7: Matching between the first and last images of the CMU House for k = 110, where the obtained matchings are connected (green: correct, red: incorrect).
More on tables

🔼 This table presents the performance comparison of three algorithms (Naive, Gumbel-Sinkhorn, and OT4P) on the task of inferring neuron identities using different proportions of known neurons (5%, 10%, and 20%). The evaluation metrics are marginal log-likelihood and precision. The results show that OT4P generally outperforms the other two algorithms, achieving higher precision and better marginal log-likelihood, especially when the proportion of known neurons is low.
read the caption
Table 2: Marginal log-likelihood and Precision (%) of algorithms for inferring neuron identities across different proportions of known neurons.

🔼 This table presents the probability of encountering the eigenvalue -1 in permutation matrices (P) and their transformed counterparts (BTP), where B is a random orthogonal matrix. The results are shown for different matrix dimensions (n = 3, 5, 10, 20, 50), demonstrating that the transformation significantly reduces the likelihood of -1 being an eigenvalue, thus improving the efficacy of the proposed method.
read the caption
Table 3: Probability (%) of eigenvalue -1 occurring in matrices.
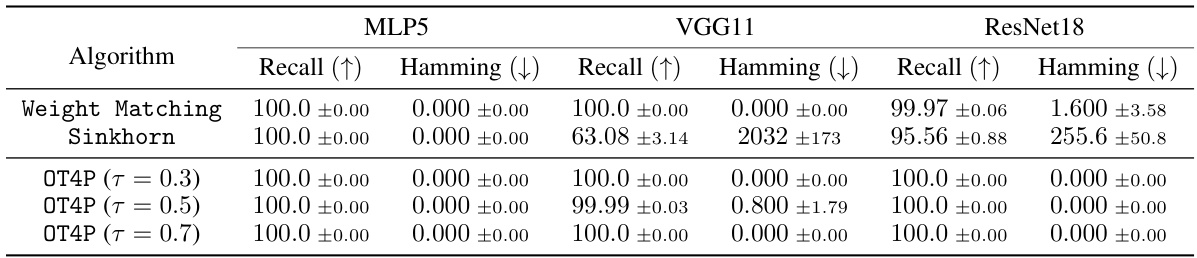
🔼 This table presents the results of comparing different algorithms for finding mode connectivity across various network architectures (MLP5, VGG11, and ResNet18). The metrics used are l1-distance (after applying a logarithmic transformation for better scaling) and precision. Lower l1-distance indicates better performance, and higher precision means a greater accuracy in finding the correct weight permutation. The results demonstrate that the proposed OT4P method outperforms the baselines (Weight Matching and Sinkhorn) in most cases.
read the caption
Table 1: l1-Distance (converted by log(1 + x)) and Precision (%) of algorithms for finding mode connectivity across different network architectures.
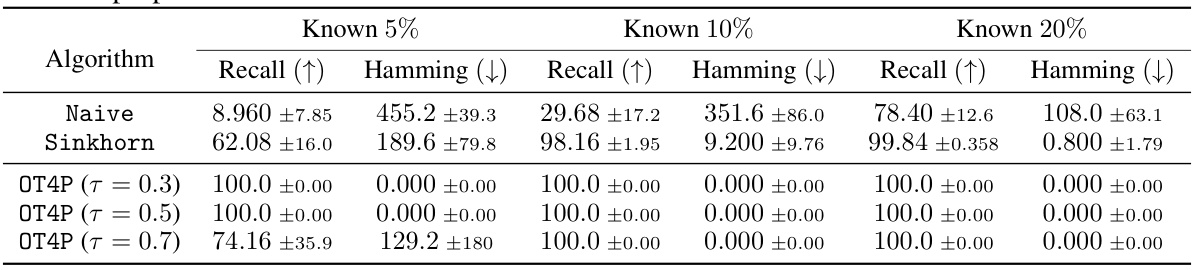
🔼 This table presents the results of three algorithms (Naive, Gumbel-Sinkhorn, and OT4P) for inferring neuron identities under different conditions (5%, 10%, and 20% known neurons). The metrics used for evaluation are Recall and Hamming Distance. The results show that OT4P generally outperforms the other algorithms across all conditions, achieving near-perfect recall in most cases, while Naive and Gumbel-Sinkhorn perform less well, especially when fewer neurons are known. The Hamming distance metric indicates how many neuron identities were incorrectly inferred.
read the caption
Table 5: Recall (%) and Hamming Distance of algorithms for inferring neuron identities across different proportions of known neurons.

🔼 This table presents the l1-distance between the matrices produced by different algorithms and their nearest permutation matrices for the largest problem instance size (a multiple of five) in each object class of the WILLOW-ObjectClass dataset. It shows how close the algorithms’ results are to actual permutation matrices, which is a measure of how well they handle the permutation relaxation task. Lower values indicate that the algorithm’s output is closer to an actual permutation matrix.
read the caption
Table 6: l1-Distance between the matrix returned by the algorithms and its closest permutation matrix. In each object class, we select the largest problem instance size that is a multiple of five.

🔼 This table compares the performance of different optimization algorithms (SGD and Adam) on the WILLOW-ObjectClass dataset for the task of permutation synchronization. It evaluates the algorithms’ F-scores across five object classes (Car, Duck, Face, Motorbike, Winebottle), showing the impact of optimizer choice on the effectiveness of each method. The largest problem instance size, that is a multiple of five, is used for each class.
read the caption
Table 7: F-scores (%) for different algorithms with various optimizers on the WILLOW-ObjectClass dataset. In each object class, we select the largest problem instance size that is a multiple of five.
Full paper#