↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world machine learning tasks involve data from diverse sources (heterogeneous data), posing challenges for model generalization. Existing invariance learning approaches rely on specific algorithms. This paper explores a fundamental question: Can standard training procedures, like Stochastic Gradient Descent (SGD), implicitly lead to invariant solutions? Over-parameterized models are often used in practice, posing challenges with limited data. The paper identifies a critical issue that using pooled data across environments can result in the model learning spurious correlations instead of generalizable patterns.
This research uses the multi-environment low-rank matrix sensing problem to study the implicit bias of SGD on heterogeneous data. They theoretically demonstrate that using large batch sizes and sequentially training SGD on data from individual environments results in implicit invariance learning. This approach avoids learning spurious signals by exploiting the heterogeneity-induced oscillation during training. The analysis shows that the model converges to an invariant solution, showcasing the benefits of heterogeneity for bias mitigation. This discovery has significant implications for understanding model generalization and building more robust models.
Key Takeaways#
Why does it matter?#
This paper is important because it reveals a novel implicit bias in standard training algorithms, potentially impacting various machine learning applications. It highlights the synergy between data heterogeneity and SGD, driving model learning towards invariant solutions without explicit regularization. This finding provides new insights into generalization and robustness and opens up avenues for designing more efficient and robust algorithms.
Visual Insights#

This figure compares the training results of two different SGD approaches: PooledSGD (left) and HeteroSGD (right). PooledSGD trains the model on a complete dataset, leading to the model fitting both core and spurious signals. In contrast, HeteroSGD trains the model sequentially on data from different environments. The changing spurious signals across environments introduce oscillations that prevent the model from fitting spurious signals and allows it to converge towards the invariant solution.
In-depth insights#
Implicit Invariance#
The concept of “Implicit Invariance” in machine learning focuses on how models implicitly learn invariant features from data without explicit programming. This is particularly relevant in scenarios with heterogeneous data, where the underlying patterns remain consistent across diverse environments but are accompanied by spurious, environment-specific variations. The core idea is that the optimization algorithm itself, such as Stochastic Gradient Descent (SGD), can exhibit an implicit bias towards invariant solutions. This bias stems from the interaction between the algorithm’s dynamics and the data’s heterogeneity. Specifically, the large step size and large batch sizes of SGD, combined with data heterogeneity, can induce oscillations that prevent the model from fitting environment-specific noise. Therefore, the model effectively converges towards a solution that captures the core, invariant aspects shared across all environments. This is significant because it suggests that explicit invariance learning mechanisms may be unnecessary in many situations, as the model naturally discovers the invariance during standard training.
SGD’s Bias#
The concept of “SGD’s Bias” in the context of machine learning, specifically concerning overparameterized models, is crucial. Stochastic Gradient Descent (SGD), while efficient, doesn’t arbitrarily select a solution; it exhibits an implicit bias. This means that even without explicit regularization, SGD tends to favor certain solutions, often simpler ones, which can lead to generalization. The paper delves into how this bias interacts with data heterogeneity. It reveals that data heterogeneity itself, particularly with a large batch size and appropriately large learning rate, can create sufficient oscillations to prevent SGD from overfitting to spurious, environment-specific aspects. This counter-intuitively leads to the learning of invariant, robust features, even if the individual environments are diverse and noisy. The interplay between SGD’s inherent bias and data heterogeneity emerges as the central theme of this “SGD’s Bias” concept, illustrating that carefully designed training procedures and algorithm choices can leverage inherent algorithmic properties for better generalization performance.
HeteroSGD#
HeteroSGD, as a proposed algorithm, stands out for its unique approach to handling heterogeneous data in multi-environment matrix sensing. Unlike traditional methods that pool data from various environments, HeteroSGD processes data sequentially, employing a large step size and large batch Stochastic Gradient Descent (SGD) in each environment. This strategy is crucial, preventing the model from fitting spurious, environment-specific signals. Instead, the heterogeneity itself, in combination with the algorithm’s implicit bias, drives the model towards an invariant solution, representing the core relations consistent across all environments. This implicit invariance learning is a key contribution, showcasing how heterogeneity can be leveraged effectively, rather than being treated as a hindrance to robust model training. The algorithm’s success hinges on the theoretical underpinning demonstrating that the oscillating effects of environment-specific data prevents overfitting, allowing the model to ultimately converge to the desired invariant representation.
Multi-env Matrix Sensing#
The heading ‘Multi-env Matrix Sensing’ suggests a research focus on adapting matrix sensing techniques to handle data from multiple environments. This likely involves scenarios where the underlying data-generating process exhibits variations across environments, such as different noise levels, distributions, or signal characteristics. The core challenge lies in designing robust matrix sensing methods capable of recovering the underlying low-rank signal consistently across diverse environments. The ‘multi-environment’ aspect highlights a key departure from standard matrix sensing, demanding new algorithms and theoretical analyses. The success of these methods likely hinges on addressing the heterogeneity inherent in the data while maintaining an efficient and generalizable approach. A crucial aspect of the research will involve analyzing and characterizing the sources of environmental variations in matrix entries, potentially using assumptions about the data structure and correlations to guide the development of robust estimation procedures. The ultimate goal is to develop practical, efficient algorithms and provide theoretical guarantees demonstrating consistent and accurate signal recovery even with varying environmental conditions. Furthermore, this research likely tackles limitations of existing matrix sensing techniques when confronted with real-world data’s complexity and inherent variability. The emphasis would be on how to disentangle shared information from environment-specific noise, creating solutions that are both accurate and reliable in diverse situations.
Future Directions#
Future research could explore the impact of different optimization algorithms beyond SGD, investigating whether similar implicit biases towards invariance exist. Analyzing the role of varying batch sizes and learning rates in the context of heterogeneous data would also provide further insight. Furthermore, extending the theoretical framework to encompass more complex model architectures, such as deep neural networks, is crucial. Addressing the challenges posed by label noise and real-world data distributions with high dimensionality would lead to more robust and practical applications of implicit invariance learning. Finally, examining the interplay between implicit biases and explicit regularization techniques could reveal powerful strategies for learning robust and generalizable models.
More visual insights#
More on figures
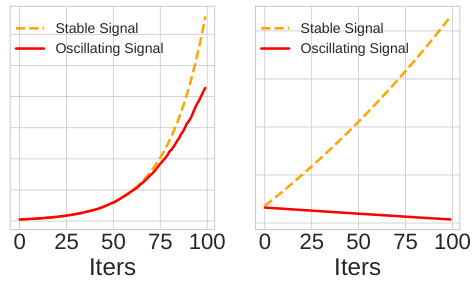
This figure compares the training process of a model using aggregated data versus heterogeneous data. The left panel shows the training on complete datasets, leading to a stable spurious signal that the model fits. The right panel shows a two-environment setting where the spurious signal fluctuates at each step, preventing the model from learning it. This highlights the implicit bias of heterogeneity towards invariance learning.
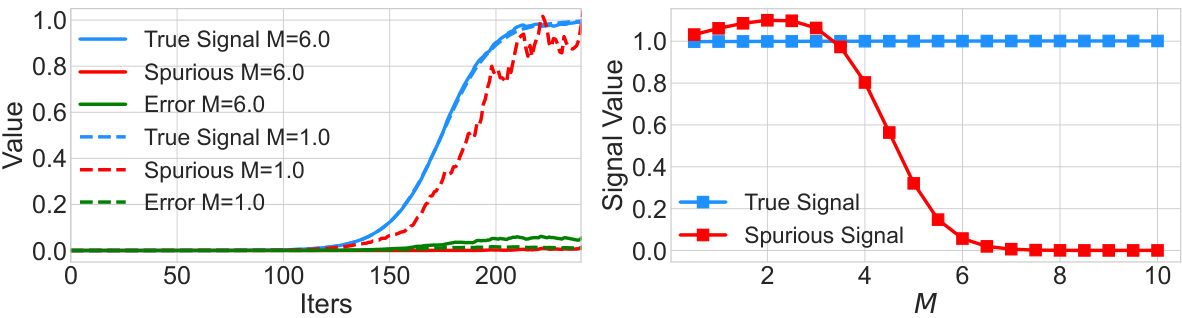
This figure compares the performance of the proposed HeteroSGD algorithm under different levels of heterogeneity (M) in a multi-environment matrix sensing problem. The left panel shows the trajectories of the true signal, spurious signal, and error terms over iterations. When the heterogeneity is high (M=6.0), the algorithm successfully separates the invariant true signal from the varying spurious signal, showing the effect of heterogeneity in preventing the model from fitting spurious signals. When heterogeneity is low (M=1.0), both true and spurious signals increase, illustrating the lack of sufficient heterogeneity to drive implicit invariance learning. The right panel summarizes the average final signal value attained as a function of heterogeneity. A phase transition is observed around M=5.0, where the spurious signal is effectively suppressed with higher heterogeneity.
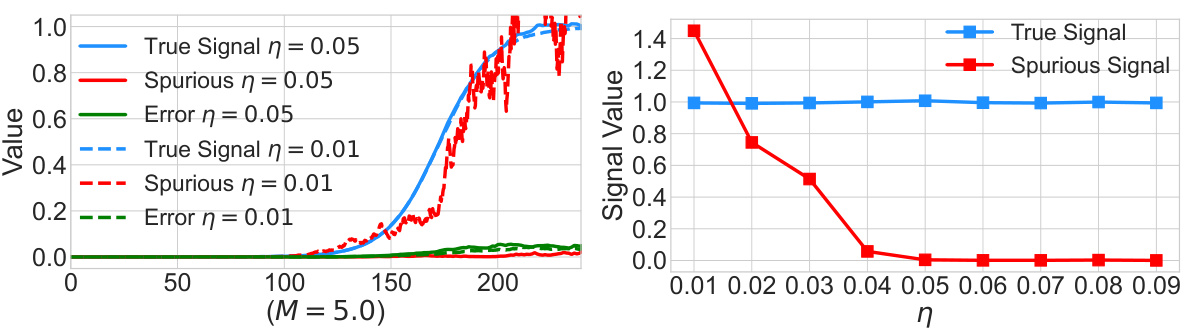
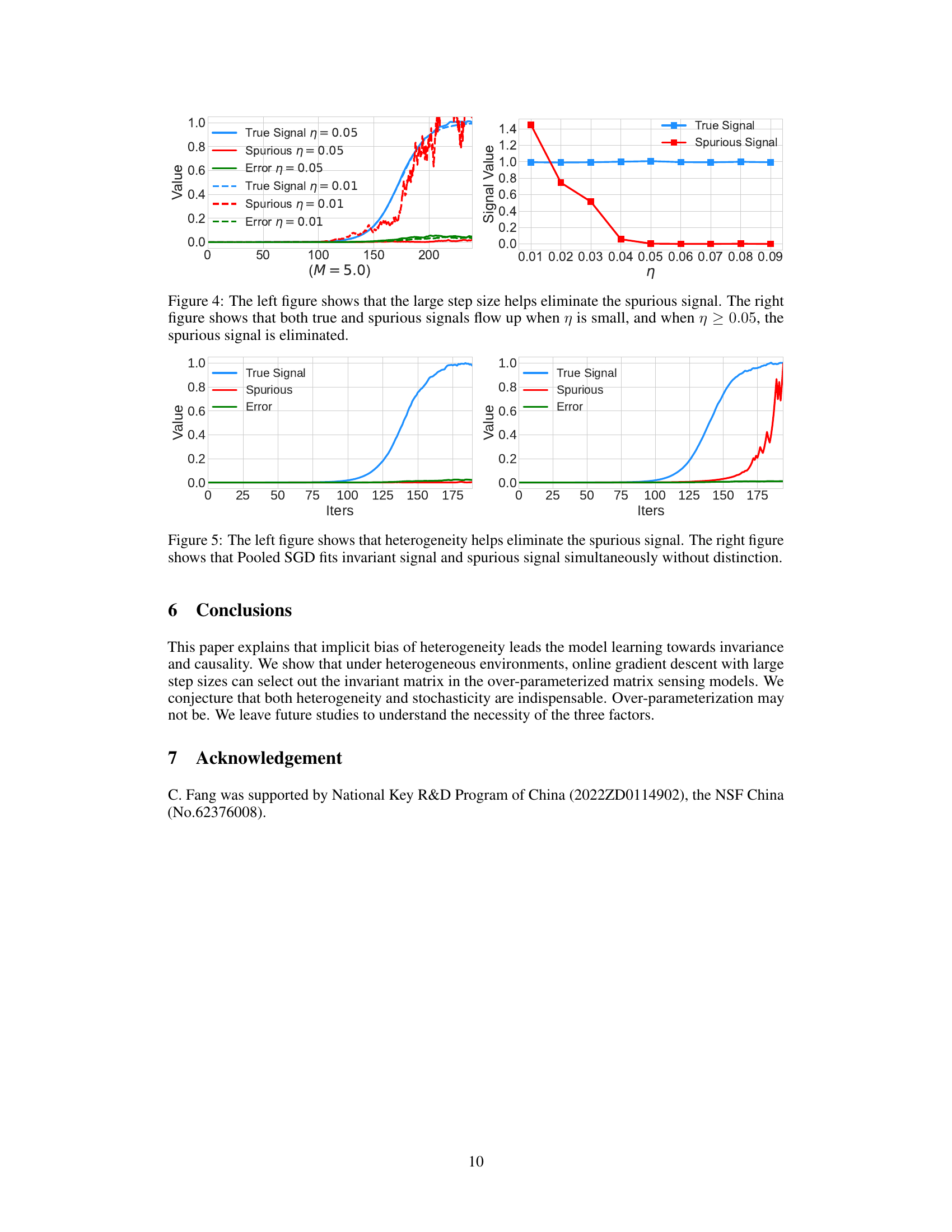
This figure compares the impact of heterogeneity (M) and learning rate (η) on signal recovery in a multi-environment matrix sensing problem. The left panel shows that with sufficient heterogeneity, the spurious signal is suppressed while the true signal is recovered. The right panel shows that a higher learning rate is needed to eliminate the spurious signal when heterogeneity is low.
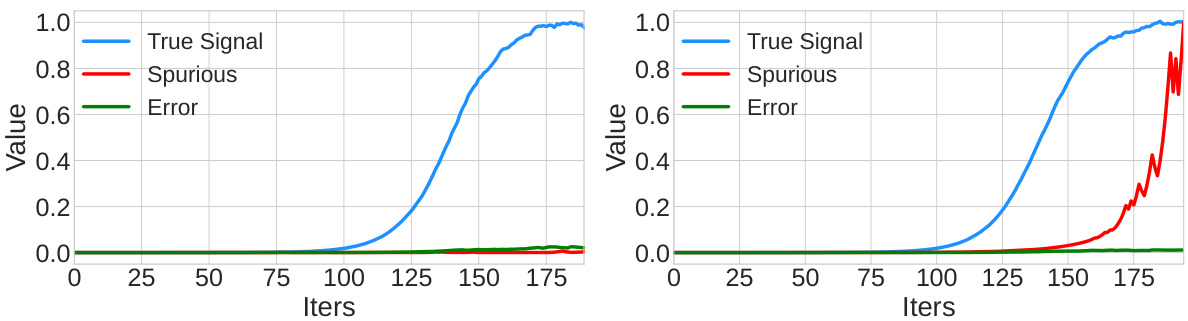
This figure compares the training results of two different methods: PooledSGD (left) and HeteroSGD (right). PooledSGD trains on data from all environments at once, leading to the model fitting spurious signals. In contrast, HeteroSGD trains sequentially on data from each environment, causing oscillations in the spurious signal that prevent overfitting and allowing the model to learn the invariant core signal.

This figure shows the result of applying PooledSGD with different step sizes (η = 0.01, 0.05, 0.1) and a batch size of 80. The left panel displays the Frobenius norm of the difference between the estimated matrix (UTU) and the true invariant matrix (A*). The right panel shows the Frobenius norm of the difference between the estimated matrix (UTU) and the sum of the true invariant matrix (A*) and the average spurious matrix (Ā). The plots demonstrate that when the batch size is small, the algorithm’s trajectory deviates significantly from both the true invariant matrix and the sum of the true invariant matrix and the average spurious matrix, indicating instability.
Full paper#