↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Probabilistic inference in high-dimensional time series is computationally expensive. Existing generative models require complex calculations, hindering scalability and real-world applications. This study addresses these challenges by leveraging contrastive learning, a discriminative method known for learning effective representations.
The researchers propose a novel approach using contrastive learning for time series data. They demonstrate that the resulting representations follow a Gauss-Markov chain, which is a type of graphical model where inferences (e.g., prediction and planning) can be simplified to inverting a low-dimensional matrix. They further validate their theoretical findings with experiments on tasks of up to 46-dimensions, outperforming conventional methods.
Key Takeaways#
Why does it matter?#
This paper is important because it demonstrates how contrastive learning can enable efficient probabilistic inference in high-dimensional time series data. This is a significant advance with implications for various fields, opening new avenues for research in planning, prediction, and control. The closed-form solutions for inference provided by the paper offer significant computational advantages, making the approach scalable to complex real-world applications.
Visual Insights#

This figure illustrates the core idea of the paper: using contrastive learning to learn low-dimensional representations of high-dimensional time series data. The learned representations are shown to follow a Gauss-Markov chain, allowing for efficient inference (e.g., prediction, planning) by simple matrix inversion or linear interpolation in the latent space. The figure visually depicts the mapping from high-dimensional observation space to a low-dimensional latent space where planning becomes easier.
In-depth insights#
Contrastive Inference#
Contrastive inference leverages the power of contrastive learning to perform probabilistic inference on time series data. It addresses the challenge of high-dimensional data by operating on learned representations that capture sufficient temporal relationships. The method’s strength lies in its ability to provide compact closed-form solutions for inference tasks, unlike traditional generative methods that can be computationally expensive. By framing inference as a Gaussian process operating on low-dimensional representations, this approach enables efficient prediction and planning. The theoretical foundation relies on key assumptions about the distribution of representations, which when met, allow for elegant mathematical solutions to inference problems. This approach’s efficiency offers significant advantages in high-dimensional domains, facilitating applications in fields like robotics and scientific modeling.
Gaussian Encodings#
The concept of “Gaussian Encodings” in a research paper likely refers to a method of representing data using Gaussian distributions. This approach is particularly valuable when dealing with high-dimensional data, a common challenge in machine learning and time series analysis. The key advantage is that Gaussian distributions are mathematically tractable, allowing for elegant closed-form solutions to otherwise complex problems. The paper might explore how encoding data as Gaussians simplifies operations like prediction, interpolation, or planning in latent space. A crucial aspect would be how the parameters of these Gaussian distributions (mean and covariance) are learned, potentially through techniques like contrastive learning or variational autoencoders. The effectiveness hinges on the assumption that the data, after encoding, closely follows Gaussian distributions. This assumption, if not fully met, could introduce limitations to the approach’s generalizability. The paper likely validates this approach through experiments demonstrating improved performance in specific tasks compared to alternative methods, particularly in high-dimensional scenarios where other techniques struggle. Successfully using Gaussian encodings could mean achieving computationally efficient inference while retaining uncertainty estimates, a significant advancement in fields like robotic control, time series forecasting, or astrophysics.
Temporal Planning#
Temporal planning, in the context of AI and robotics, focuses on generating sequences of actions over time to achieve a goal. It is a complex problem because it requires reasoning about the dynamics of the environment and the effects of actions, often in high-dimensional spaces. A key challenge is handling uncertainty, both in the model of the environment and in the execution of actions. Contrastive learning offers a promising approach by learning representations that encode relevant temporal relationships, enabling efficient inference of future and intermediate states. This approach shifts focus from reconstructing complex high-dimensional states to reasoning directly within a lower-dimensional representation space, making planning more tractable and potentially more robust to noise and uncertainty. This is especially helpful for high-dimensional problems in robotics and other areas. Furthermore, the Gaussianity assumption simplifies calculations and inference within this latent space, enabling closed-form solutions for planning. However, these methods rely on assumptions like the marginal distribution over representations being Gaussian, which may not hold true for all real-world applications.
High-dim. Results#
A hypothetical ‘High-dim. Results’ section in a research paper would likely present empirical evidence demonstrating the effectiveness of a proposed method on high-dimensional datasets. The core of this section would be showcasing successful application to problems with a significantly larger number of dimensions than those typically used in baseline experiments. Key aspects would involve comparisons against existing state-of-the-art techniques, assessing performance metrics like accuracy, efficiency, and scalability, as well as demonstrating that the method maintains robust performance even with the increase in dimensionality. The section should also address whether the high dimensionality introduces any new challenges or limitations, requiring specific modifications to the original method. Visualizations, such as plots of performance metrics across different dimensions or error rates against dimensionality, would be essential for a clear and effective presentation. Finally, a discussion explaining any unexpected results or challenges faced in scaling up to high-dimensional settings would add crucial depth and analytical rigor to the section, highlighting the practical impact and robustness of the contribution.
Limitations#
A research paper’s ‘Limitations’ section is crucial for establishing credibility. It should explicitly address any shortcomings, acknowledging assumptions, constraints, and unresolved questions. A thoughtful limitations section demonstrates a deep understanding of the study’s scope and potential biases. For instance, it might discuss the generalizability of findings, highlighting whether results apply only to specific contexts or populations. Another key aspect is methodological limitations, such as sample size or potential biases in data collection. Addressing the practical applicability of results is also vital, showing awareness of real-world constraints and potential challenges in implementation. Transparency in this section helps readers assess the study’s strengths and weaknesses accurately, contributing to a more robust and nuanced understanding of the research.
More visual insights#
More on figures

This figure illustrates the concept of contrastive learning applied to time series data. Pairs of observations (x0 and xt+k) are used to learn representations (ψ(x0) and ψ(xt+k)). The key idea is that a linear transformation (A) applied to the initial representation (ψ(x0)) should closely approximate the final representation (ψ(xt+k)). The figure highlights the advantage of working in a lower-dimensional latent space. While directly interpolating waypoints in the original high-dimensional space is difficult, it becomes a simple linear interpolation in the latent space.

This figure illustrates the core idea of the paper: using temporal contrastive learning to learn low-dimensional representations of high-dimensional time series data. The learned representations, denoted ψ(x), are designed such that the transformation Aψ(x0) approximates the representation of a future state, ψ(xt+k). The key result is that the distribution over intermediate representations between ψ(x0) and ψ(xt+k) has a closed-form solution and can be computed via linear interpolation, simplifying inference tasks.

This figure shows the results of numerical simulations on a toy dataset of outwardly spiraling trajectories. Temporal contrastive learning is applied, and the learned representations are used for forward prediction, backward prediction (inferring past states), and planning (inferring intermediate waypoints between a start and end state). The results demonstrate that the learned representations effectively capture the underlying structure of the data, allowing for accurate probabilistic inference.
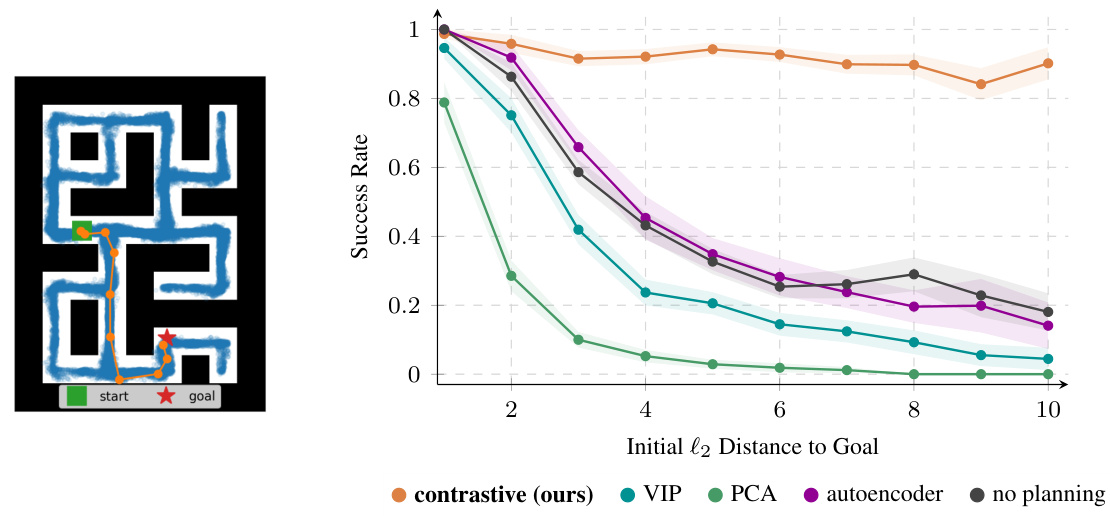
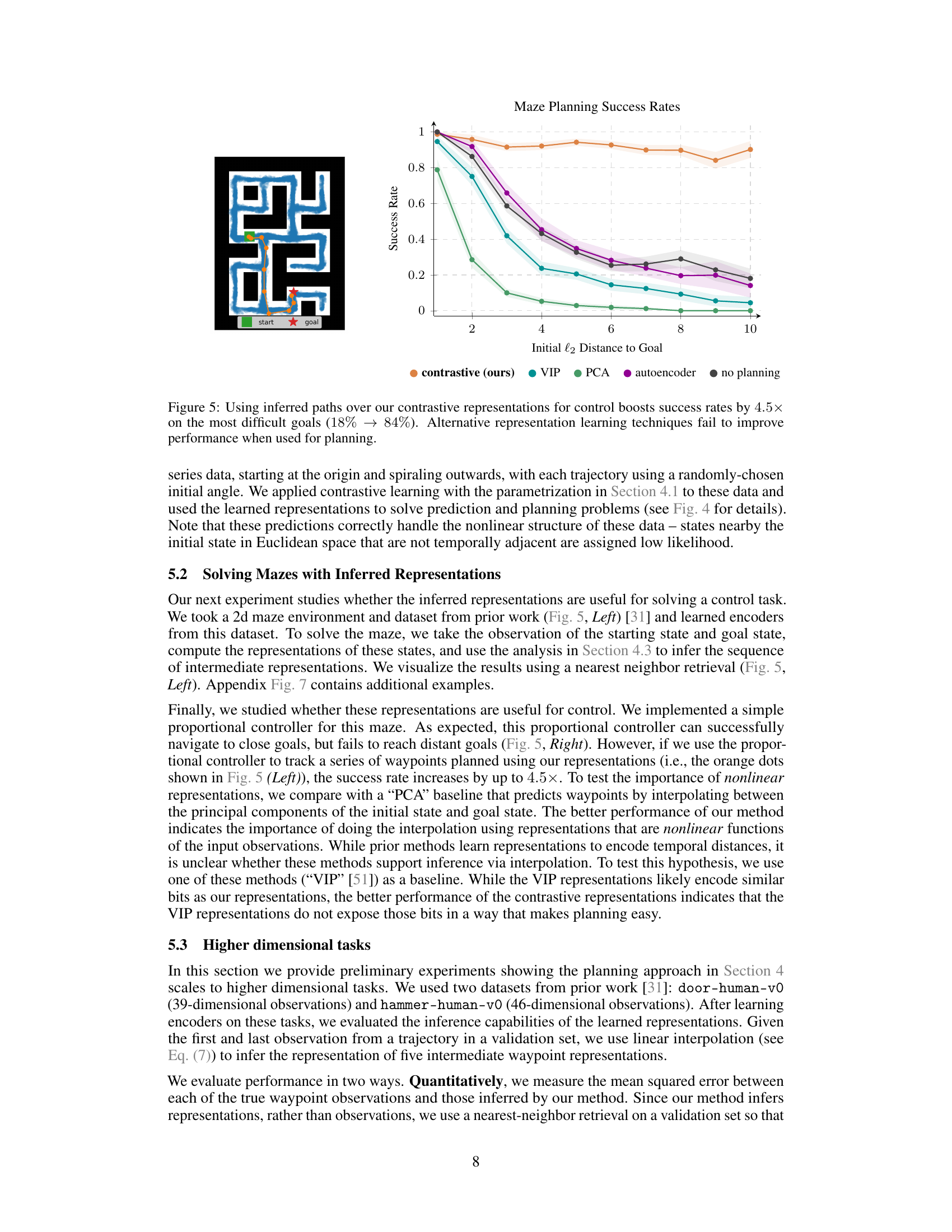
This figure shows the results of an experiment where the authors used inferred paths from contrastive representations for a control task in a maze environment. The x-axis represents the initial Euclidean distance to the goal in the maze, while the y-axis shows the success rate of reaching the goal. Different colored lines represent different methods: contrastive (ours), VIP, PCA, autoencoder, and no planning. The figure demonstrates that using the inferred paths from contrastive representations significantly improves the success rate, particularly for goals that are farther away.

This figure shows the results of a planning task in a 39-dimensional robotic door opening scenario. It compares the proposed contrastive planning method with three baselines (no planning, PCA planning, and VIP planning) in terms of waypoint prediction accuracy. The figure displays a dataset of trajectories, the mean squared error (MSE) of waypoint prediction for each method, and a t-SNE visualization showing the learned representations and the inferred plans.

This figure shows five examples of a robot navigating a maze. The robot starts at a green square and must reach a red star. The blue lines indicate the path that the robot would take without the use of the proposed method. The orange dots and lines represent the planned path based on the proposed approach using contrastive representations to interpolate between the start and goal. The result shows that the use of the inferred waypoints helps the robot successfully navigate to the goal, even when it is more distant than in previous examples.. This illustrates how contrastive representations can make planning simpler in complex environments.

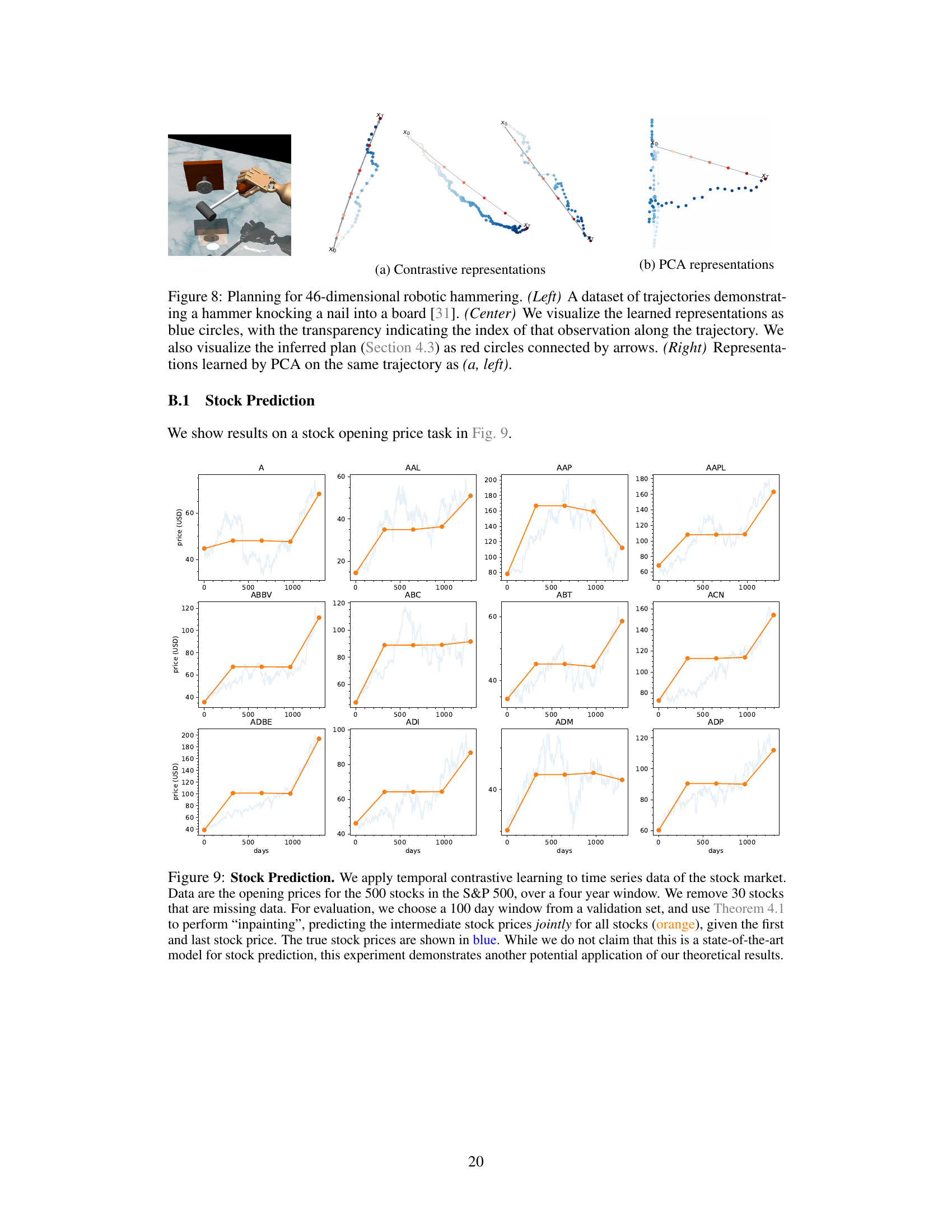
This figure demonstrates the results of applying contrastive learning and PCA to a 46-dimensional robotic hammering dataset. Panel (a) shows the learned contrastive representations, visualized as a trajectory with intermediate states inferred using the method described in the paper. The transparency of the points indicates the position in the time series. The inferred plan (intermediate states) are represented by red circles connected by arrows. Panel (b) shows the results obtained using PCA, which does not capture the same nonlinear trajectory. The figure aims to illustrate that contrastive representations are superior to PCA representations for the task of planning or interpolating in high-dimensional state spaces.

This figure shows numerical simulations validating the paper’s theoretical results. A toy dataset of spiraling trajectories is used to demonstrate the effectiveness of contrastive learning in predicting future and past states, as well as inferring intermediate states (waypoints) between given initial and final states. The distributions generated from the learned representations accurately reflect the structure of the data.
Full paper#