From Transparent to Opaque: Rethinking Neural Implicit Surfaces with $lpha$-NeuS

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it significantly advances 3D reconstruction techniques by addressing a long-standing challenge: reconstructing both transparent and opaque objects simultaneously. Its novel method, a-NeuS, offers improved accuracy and efficiency, opening new avenues for various applications, including augmented reality, virtual reality, and medical imaging. The public availability of the code and benchmark data further facilitates wider adoption and future research.

Visual Insights

#

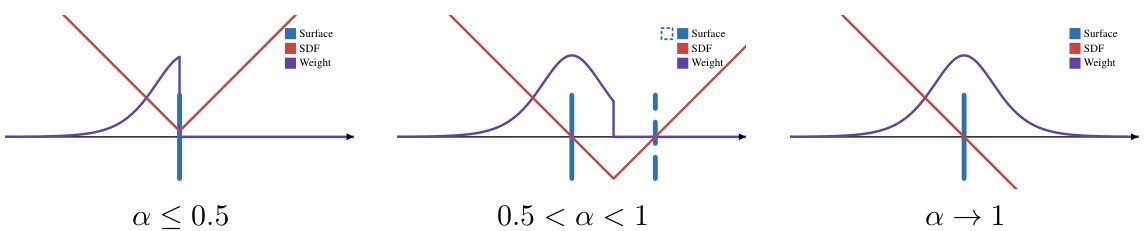
This figure illustrates how the signed distances and rendering weights change along a ray passing through an object with varying opacity (α). When α ≤ 0.5, the front and back faces coincide, and the maximum weight aligns with the local minimum of the distance field. As α increases (0.5 < α < 1), the back face moves further away, and the maximum weight shifts to the zero-distance point. Finally, when α → 1 (fully opaque), the back face is infinitely far, and the scene simplifies to a single ray-plane intersection.

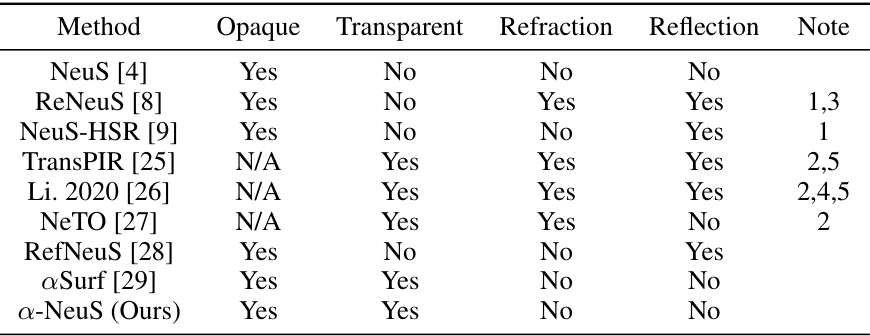
The table compares the capabilities of various methods in 3D reconstruction, focusing on their ability to handle opaque and transparent objects, refraction, and reflection effects. It highlights whether each method successfully reconstructs opaque objects, transparent objects, or both, and whether it accounts for refraction and/or reflection. Notes clarify specific assumptions made by certain methods.

In-depth insights

#

α-NeuS: Intro

#

The hypothetical introduction section, “α-NeuS: Intro,” would likely begin by highlighting the limitations of existing neural implicit surface methods, particularly their struggles with representing transparent objects. It would then introduce α-NeuS as a novel approach designed to overcome these limitations by enabling the simultaneous reconstruction of both opaque and thin transparent surfaces. The introduction would emphasize that this is achieved by leveraging a theoretical understanding of how transparent surfaces manifest as local extrema within the learned distance fields, differentiating them from opaque surfaces aligned with zero level sets. A key claim would likely be α-NeuS’s ability to produce unbiased surface reconstructions for both material types, supported by a new theoretical framework extending prior work. Finally, the introduction would briefly touch upon the experimental setup and the benchmark dataset used for validation, emphasizing the practical utility of α-NeuS.

Unbiased Surface

#

The concept of “unbiased surface” in 3D reconstruction is crucial for accurately representing objects from multi-view images. Traditional methods often struggle with transparent or partially transparent objects, leading to biased or incomplete surface estimations. The core idea is to identify surface points where the rendering weights achieve local maxima, ensuring that the reconstructed surface aligns well with the true object boundaries. This is particularly challenging for transparent objects, as they induce local extreme values (minima or maxima) in the learned distance fields, unlike opaque surfaces which usually align with zero level sets. The innovation lies in a novel optimization method that accurately extracts these level sets, regardless of whether the local minima are non-negative or zero, producing unbiased surface reconstructions for both transparent and opaque materials. This addresses a significant limitation in existing neural implicit surface methods, improving the overall accuracy and completeness of 3D models generated from multi-view data.

Opacity’s Role

#

The concept of ‘Opacity’s Role’ in the context of neural implicit surface reconstruction is crucial. Opacity is not merely a visual attribute but a fundamental factor influencing the shape reconstruction process. Transparent objects, unlike opaque ones, introduce complexities due to light refraction and transmission. Traditional methods struggle with these complexities, often resulting in incomplete or inaccurate surface representations. The paper likely highlights how the variation in opacity across different materials directly impacts the learned distance fields. Areas with higher opacity will show stronger signals in the distance fields, while transparent regions will exhibit weaker or ambiguous signals. This understanding is vital for developing algorithms that can effectively handle a wide range of materials, improving the accuracy and completeness of 3D model reconstructions. Furthermore, the ‘Opacity’s Role’ likely explores the mathematical relationship between opacity and the underlying data representation, enabling the development of robust optimization techniques. This sophisticated handling of opacity allows the reconstruction of both transparent and opaque elements within a unified framework.

Benchmarking

#

A robust benchmarking strategy is crucial for evaluating the effectiveness of novel 3D reconstruction methods, especially those handling transparent objects. A comprehensive benchmark should include both synthetic and real-world datasets, varying in complexity, object types, and lighting conditions. Synthetic datasets offer controlled environments for precise quantitative evaluation, allowing for isolating and analyzing specific aspects like material properties or lighting effects. Real-world datasets provide a more challenging, realistic testbed, assessing the algorithm’s generalizability and robustness to noise and variations present in natural images. Quantitative metrics such as Chamfer distance are essential to measure surface accuracy, comparing reconstructed surfaces to ground truth models. However, purely quantitative metrics may not fully capture perceptual quality. Thus, qualitative visual comparisons should also be included. Finally, publicly available datasets and code are highly recommended to promote reproducibility and facilitate further research in the field.

Future Work

#

The paper’s core contribution is a-NeuS, a novel method that successfully reconstructs both transparent and opaque objects simultaneously. Future work could focus on several key areas: First, extending the method’s capabilities to handle complex refraction and reflection effects, currently not addressed, would significantly enhance its versatility. Second, improving the efficiency and scalability of the optimization process is crucial, particularly for larger, more complex scenes. Third, exploring the application of a-NeuS to different modalities beyond multi-view images could broaden its impact. This may involve integrating depth sensors or other data sources to improve reconstruction accuracy. Finally, a thorough ablation study is warranted to analyze the specific contribution of each component in a-NeuS and identify potential avenues for further optimization. This could involve testing the algorithm with varying levels of opacity and comparing it to existing methods under controlled conditions.

More visual insights

#

More on figures

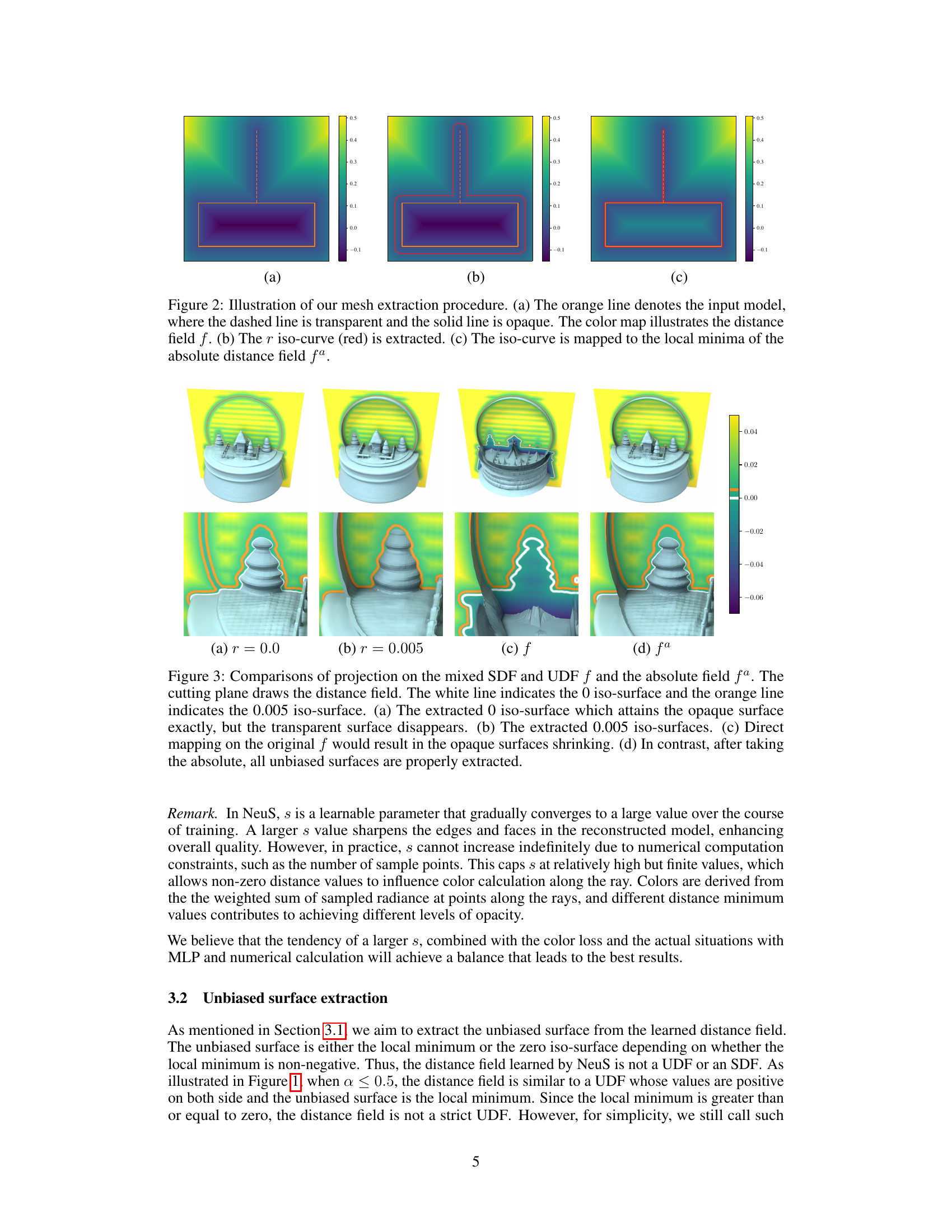
This figure illustrates the mesh extraction process of the proposed method. It shows how the method extracts the iso-curve from the distance field and then maps it to the local minima of the absolute distance field to obtain the final mesh, effectively handling both transparent and opaque objects.

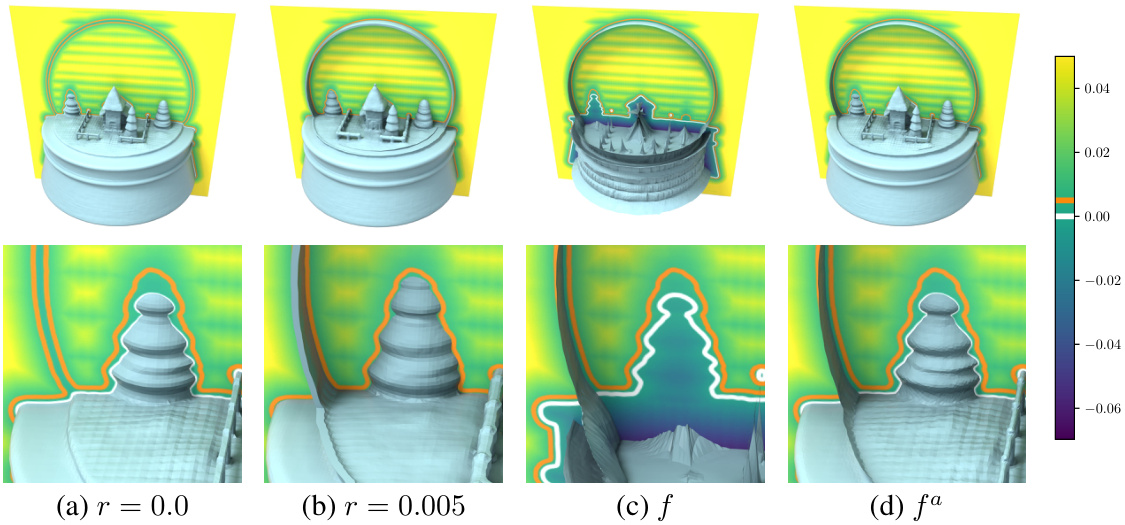
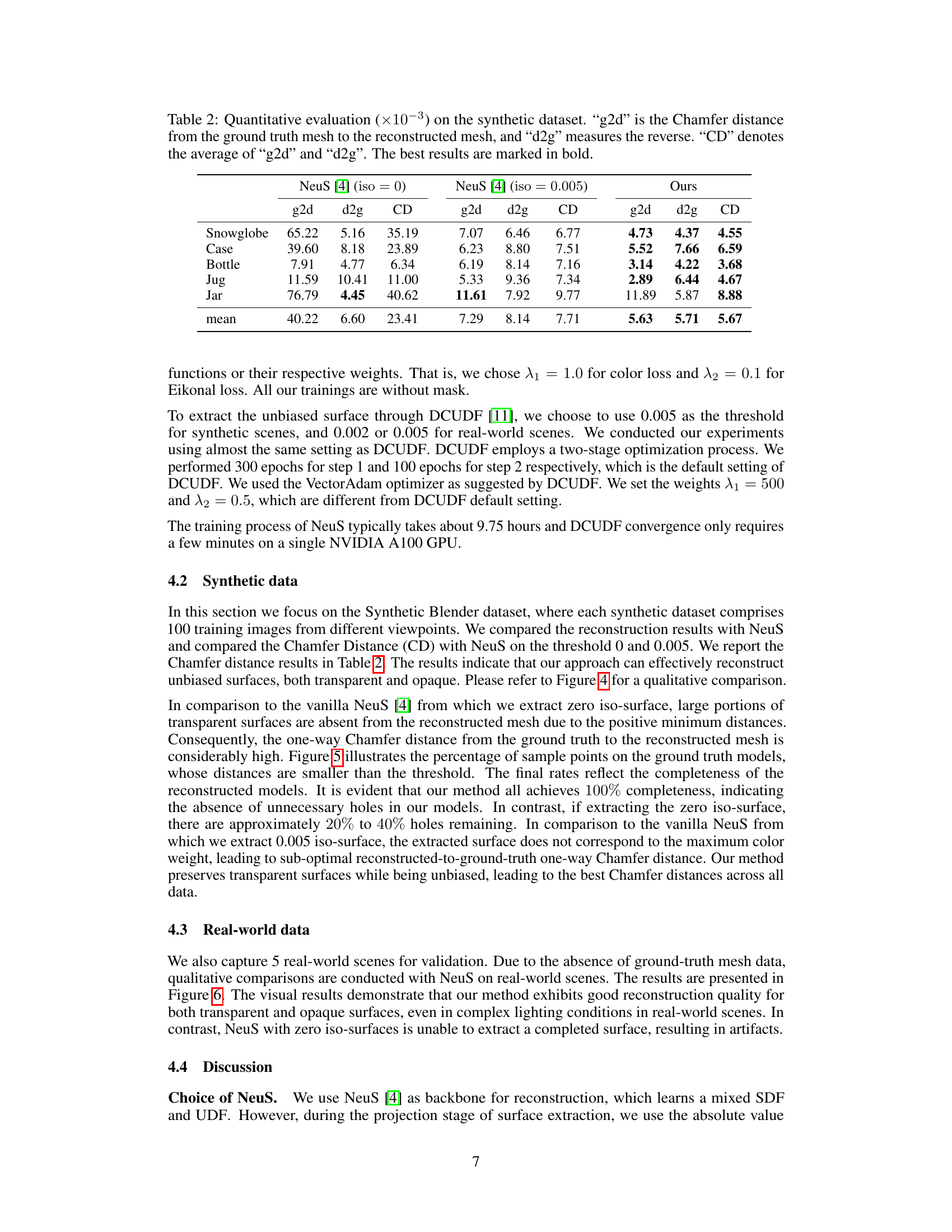
This figure compares the results of projecting onto the mixed SDF and UDF (f) and the absolute field (fa). It demonstrates that using the absolute value of the distance field (fa) allows for the proper extraction of both opaque and transparent surfaces, unlike using the original distance field (f) which causes the opaque surfaces to shrink and loses the transparent surface.

This figure compares the results of the proposed method against NeuS on synthetic data. It visually demonstrates that while NeuS can reconstruct transparent surfaces, it struggles to extract them when the local minima in the distance field are positive. The proposed method addresses this issue by leveraging a novel algorithm that extracts surfaces corresponding to both non-negative local minima and zero iso-values in the distance field, leading to more complete reconstructions.

This figure shows the percentage of sample points from the ground truth models whose distances to the reconstructed meshes are below certain thresholds. The blue line represents the proposed method (Ours), and the orange line represents the method using the zero iso-surface. The x-axis shows the thresholds, and the y-axis shows the percentage of points meeting that threshold. The figure demonstrates that the proposed method achieves 100% completeness for all models, indicating the absence of any holes, while the zero iso-surface method has significant incompleteness (20-40% holes).

This figure compares the results of the proposed method (α-NeuS) with the baseline method (NeuS) on synthetic datasets. The normal maps visualize the distance fields, showcasing how NeuS struggles to reconstruct transparent objects where the local minima in the distance field are positive. α-NeuS, on the other hand, addresses this limitation by extracting both the non-negative local minima and the zero iso-surfaces, resulting in improved reconstruction of both transparent and opaque regions.

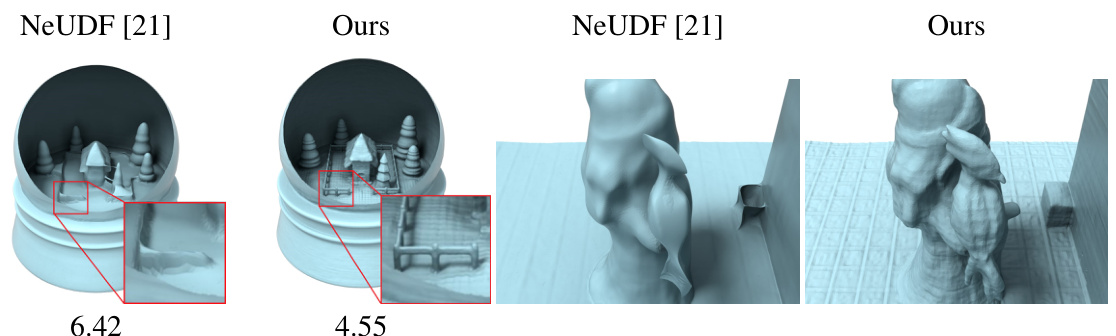
This figure compares the results of the proposed method and NeUDF for reconstructing transparent objects. The left two images show a snow globe, with the proposed method exhibiting better reconstruction of details, especially at the base, compared to NeUDF. The rightmost images show a statue, with similar results; the proposed method reconstructs a cleaner, more complete statue. Chamfer distances are provided quantitatively below each pair of images, indicating that the proposed method performs better.

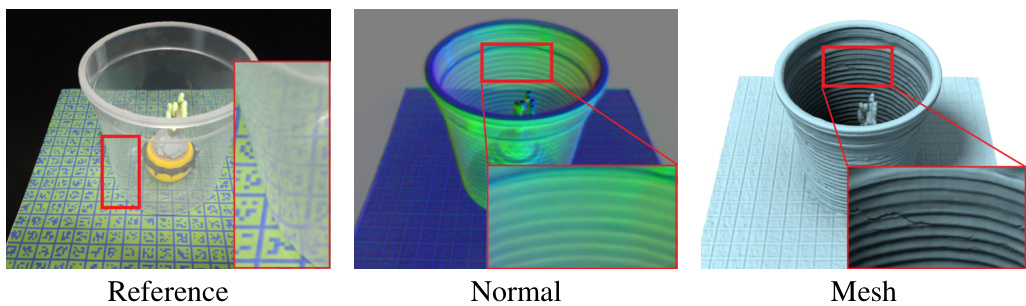
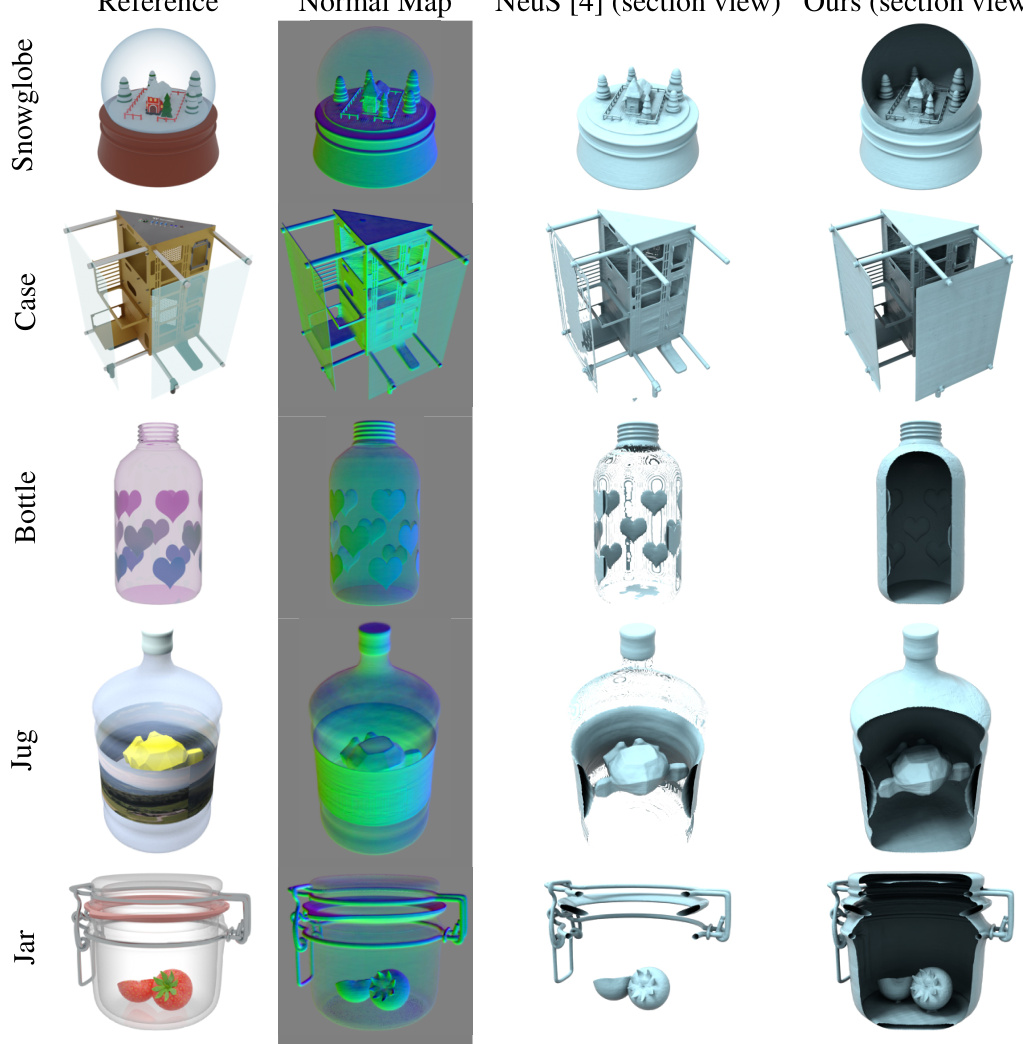
This figure shows a qualitative comparison of the results of the proposed method, a-NeuS, with the baseline methods (NeuS and Normal Map) on real-world data. The results demonstrate the effectiveness of a-NeuS in reconstructing both transparent and opaque objects accurately, preserving fine details compared to the other approaches. The figure highlights improvements in handling complex lighting conditions and intricate surface structures, which often cause issues in traditional reconstruction techniques.

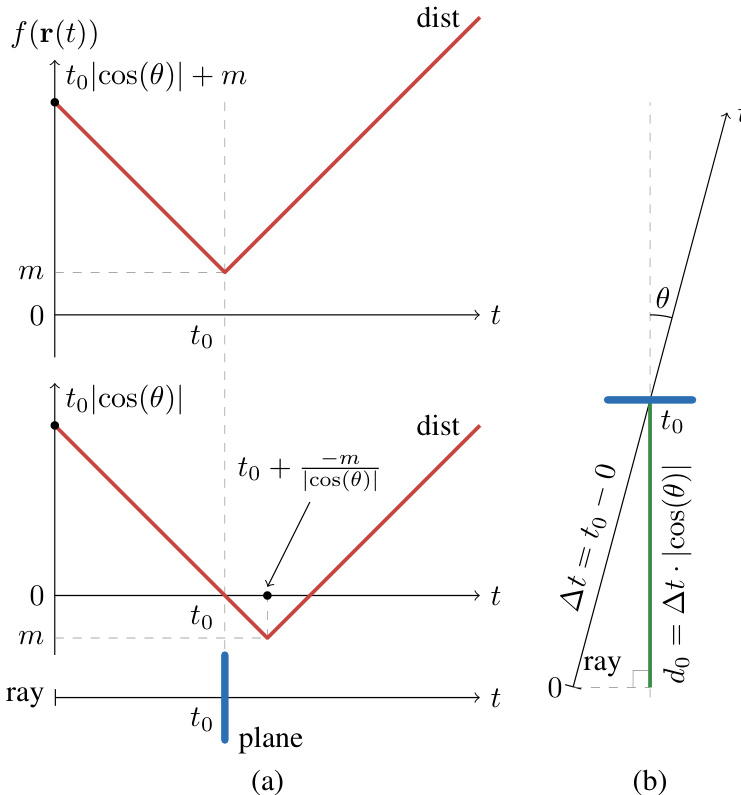
This figure illustrates the distance functions used in the proof of Theorem 1, which discusses the unbiasedness of the density function in NeuS for both transparent and opaque surfaces. Subfigure (a) shows two curves representing the distance function for cases where the local minimum (m) is positive and negative. Subfigure (b) provides a geometric interpretation, showing the relationship between the distance from the ray origin to the plane (do), the intersection point (to), and the angle between the ray and the plane (θ). These diagrams help visualize the calculations involved in determining the opacity (α) for both transparent and opaque cases.

This figure displays additional results comparing the proposed ‘-NeuS’ method with the NeUDF method for 3D reconstruction of objects. The Chamfer distances, which measure the difference between the reconstructed mesh and ground truth, are shown for several models. The results suggest that ‘-NeuS’ achieves better reconstruction accuracy.

This figure shows a comparison of the reconstruction results for an empty transparent jar using three different methods. The reference image shows the actual jar. NeuS [4] fails to reconstruct the complete transparent structure, while the proposed method (Ours) successfully reconstructs the whole structure, including the transparent jar body and its metallic clasp.

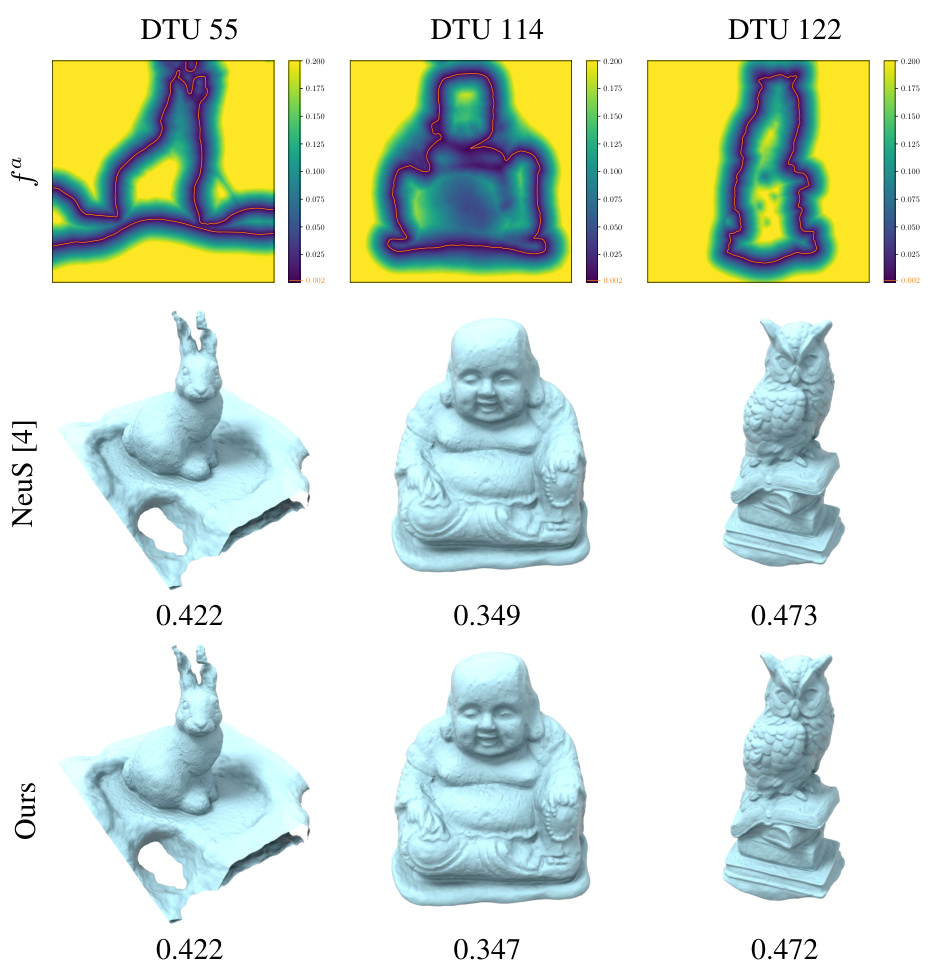
This figure compares the results of the proposed method (α-NeuS) and the original NeuS method on the DTU dataset for 3D object reconstruction. It shows three examples of 3D objects from the DTU dataset. For each object, it displays the absolute values of the signed distance field (SDF) calculated by NeuS. The color map represents the value of the distance field, with different colors corresponding to different distances. The orange line indicates the iso-surface extracted using the proposed method with a threshold of r=0.002. The Chamfer distances between the reconstructed meshes and the ground truth meshes are given for both methods below each image pair. The figure demonstrates the superiority of the α-NeuS method in accurately reconstructing the object surfaces, especially the fine details and complex geometries, compared to the original NeuS method.

Full paper

#