Group Robust Preference Optimization in Reward-free RLHF

↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in large language model (LLM) alignment because it directly addresses the critical issue of fairness and robustness in RLHF. By introducing a novel group-robust optimization method, it provides a significant advancement in ensuring equitable performance across diverse user groups. This work is highly relevant to current trends in fair and robust AI and opens new avenues for research in addressing bias and achieving more inclusive AI systems.

Visual Insights

#

This figure illustrates the core difference between traditional reward-free preference optimization methods and the proposed GRPO method. Traditional methods optimize for average performance across all groups, often leading to bias towards the majority group’s preferences. GRPO, on the other hand, focuses on the worst-performing group, adaptively weighting the importance of different groups to ensure robust and equitable alignment across all groups.

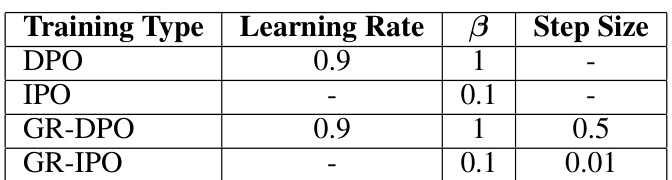
This table lists the hyperparameters used for the synthetic experiments in the paper. It includes the learning rates, beta values, and step sizes for each of the four training types: DPO, IPO, GR-DPO, and GR-IPO. The beta values are related to the regularization of the model during the training. The step sizes control the magnitude of the parameter updates during optimization. Understanding these hyperparameters is crucial for replicating the experiments and interpreting the results.

In-depth insights

#

Reward-Free RLHF

#

Reward-free RLHF offers a compelling alternative to traditional RLHF, which relies on a learned reward model. The core advantage lies in circumventing the complexities and potential pitfalls of reward model training, such as reward hacking and overfitting. By directly optimizing the policy based on human preferences without an intermediary reward function, reward-free methods enhance robustness and reduce the risk of unintended biases. However, reward-free RLHF methods often face challenges in efficiently leveraging preference data, particularly when dealing with diverse preferences among subgroups. This necessitates careful algorithmic design to ensure both efficient convergence and equitable performance across all groups. The choice of optimization algorithm becomes crucial, influencing convergence speed and overall performance. Therefore, research in reward-free RLHF is focused on developing techniques that balance efficiency with robustness, addressing scalability issues and ensuring fairness in the policy learned. The potential of reward-free RLHF lies in its ability to improve alignment with human values, particularly when diverse groups are involved, and in its reduced susceptibility to reward model misalignments.**

Group Robustness

#

The concept of ‘Group Robustness’ in the context of reward-free RLHF (Reinforcement Learning from Human Feedback) is crucial for ensuring fairness and equitable performance across diverse user groups. Traditional RLHF methods often optimize for average performance, potentially neglecting the needs of minority groups. Group Robust Preference Optimization (GRPO) addresses this by focusing on the worst-performing group, maximizing the minimal performance across all groups. This approach builds upon reward-free direct preference optimization techniques. GRPO adaptively and sequentially weights the importance of different groups, prioritizing those exhibiting poorer performance. This dynamic weighting mechanism aims to improve the performance of disadvantaged groups and reduce performance discrepancies between them. The theoretical analysis of GRPO demonstrates its convergence properties and feasibility within specific policy classes. Empirical evaluations on diverse datasets show that GRPO significantly improves the worst-performing group’s performance, reduces loss imbalances, and increases accuracy compared to non-robust baselines. Thus, the research highlights the importance of considering group-level diversity when aligning LLMs (Large Language Models) to human preferences for fairer and more inclusive AI systems.

Adaptive Weighting

#

Adaptive weighting, in the context of aligning large language models (LLMs) to diverse user groups, is a crucial technique for ensuring fairness and robustness. It addresses the inherent challenge of traditional methods that often prioritize the majority group’s preferences at the expense of minorities. By dynamically adjusting the influence of each group based on performance metrics such as loss or accuracy, adaptive weighting allows the model to learn from all groups equitably. This prevents scenarios where the model primarily reflects the preferences of dominant groups, leading to biases and inequitable outcomes. The key lies in designing an effective weighting strategy. This involves selecting appropriate metrics to track group performance and defining a mechanism for updating weights in response to observed imbalances. The weighting scheme needs to be adaptive and reactive to changes in model alignment. For example, groups with consistently high error might receive greater weights to improve their representation in subsequent updates. A well-designed adaptive weighting scheme can significantly improve overall model performance and equity across different groups. It’s vital to consider the computational costs and convergence properties of different adaptive weighting strategies when selecting an approach for LLM alignment. Furthermore, the theoretical justification and analysis of adaptive weighting schemes are important for understanding their long-term effects and ensuring reliable convergence to a fair and robust model.

Theoretical Analysis

#

A theoretical analysis section in a research paper would typically delve into the mathematical underpinnings and formal properties of the proposed methods. For a paper on reward-free RLHF, this might involve analyzing the convergence and feasibility of the proposed optimization algorithms. This could include proving convergence bounds under specific assumptions about the data distribution and the policy class. The analysis might employ techniques from convex optimization, online learning, or game theory, depending on the nature of the algorithms. Furthermore, a theoretical analysis could explore the sample complexity of the approach, determining how much data is needed to achieve a certain level of performance. Finally, this section could compare the theoretical properties of the proposed methods with existing approaches, highlighting advantages and potential limitations in a formal way. The goal is to provide a rigorous justification for the claims made about the method’s effectiveness, and potentially to identify new avenues for future improvement.

Future Directions

#

Future research could explore extending the GRPO framework to handle more complex scenarios, such as those involving hierarchical group structures or overlapping group memberships. Investigating the impact of different reward functions beyond the log-linear policy class and the effects of varying group sizes and data distributions on the algorithm’s performance would also be valuable. A deeper theoretical analysis of GRPO’s convergence properties under diverse conditions, coupled with empirical validation across a broader range of datasets and LLMs, would further solidify the findings. Developing more efficient algorithms for large-scale group-based preference optimization is crucial for real-world applications. Finally, exploring GRPO’s potential in other RLHF contexts, such as multi-objective reward learning and handling conflicting preferences, is a promising avenue for future investigation.

More visual insights

#

More on figures

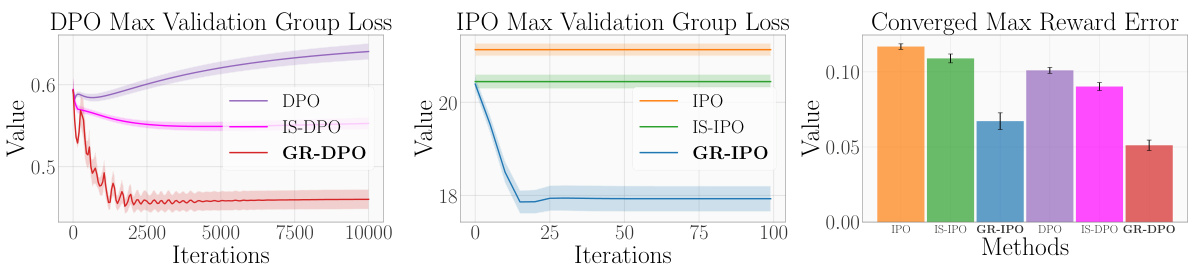
This figure displays the results of synthetic experiments comparing Algorithm 1 (GR-DPO and GR-IPO) against other methods (DPO, IPO, IS-DPO, IS-IPO) in terms of worst-case validation loss and reward error. Algorithm 1 consistently outperforms the others, demonstrating its effectiveness in handling diverse group sizes and response distributions.

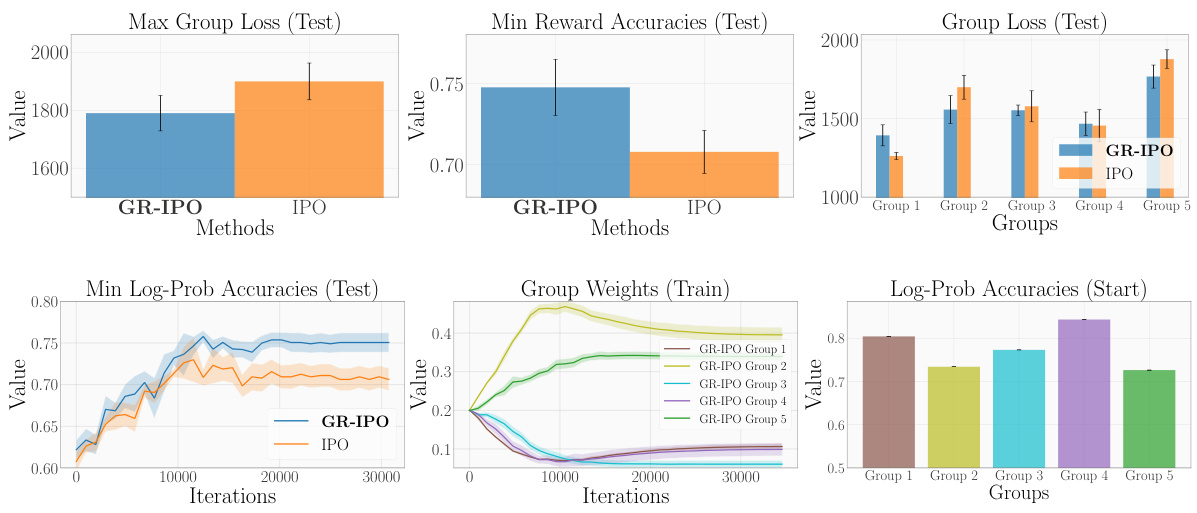
This figure shows the results of applying GR-IPO and IPO to real-world data from a global opinion survey. The top row demonstrates that GR-IPO achieves lower maximum group loss and higher minimum reward accuracy than IPO. It also shows a more balanced distribution of losses across different groups. The bottom row examines the training process itself. The left plot shows log-probability accuracy, indicating that GR-IPO improves accuracy over time for all groups. The middle plot shows the weights assigned to each group during training, illustrating that GR-IPO prioritizes underperforming groups. The right plot displays the initial log-probability accuracies before training.

The figure presents results from synthetic experiments comparing the performance of the proposed GRPO algorithm (GR-DPO and GR-IPO) to baseline methods (DPO, IPO, IS-DPO, IS-IPO). The results show that GRPO significantly reduces the maximum validation group loss and reward error, especially in scenarios with diverse group sizes and response distributions.

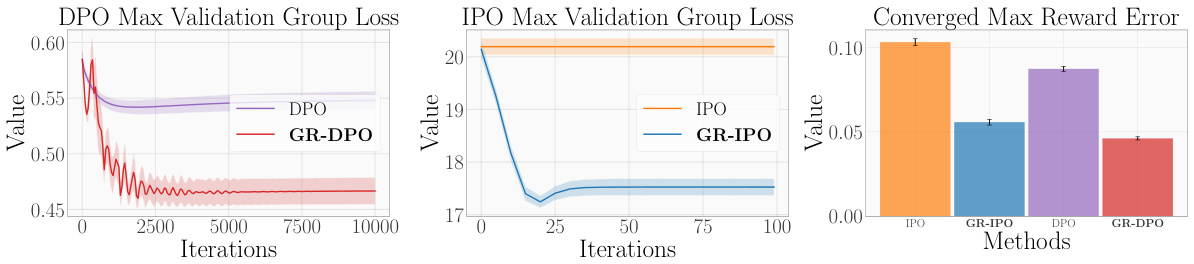
This figure displays the results of synthetic experiments comparing Algorithm 1 (GR-DPO and GR-IPO) against importance sampling methods (IS-DPO/IPO) and standard DPO and IPO methods. The results show that Algorithm 1 achieves a significantly lower worst-case validation loss and reward error. The experiment used a scenario with groups of different sizes and response distributions to test the robustness of the algorithms.

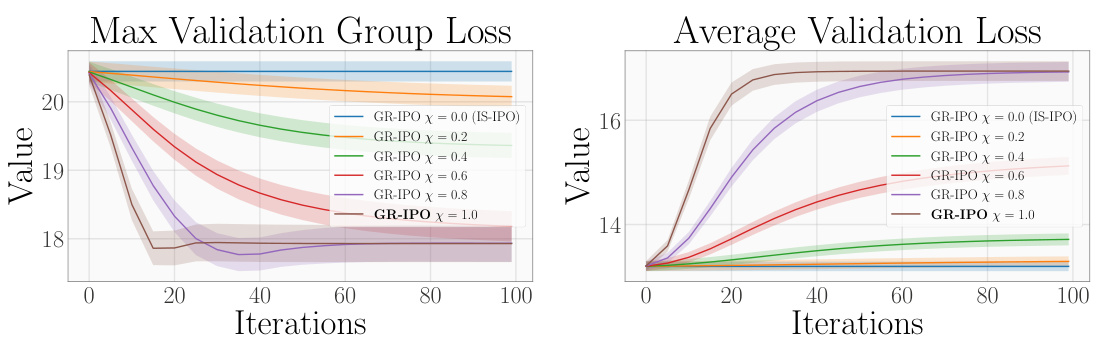
This figure shows the ablation study for the trade-off parameter ‘x’ in the synthetic experiments of the paper. The x parameter balances the worst-case and average performance of the model. The left plot shows the maximum validation group loss and the right plot shows the average validation loss. As the value of x increases, the worst-group performance improves while the average performance decreases, indicating the trade-off between these two metrics. The shaded areas represent standard deviations across multiple runs.

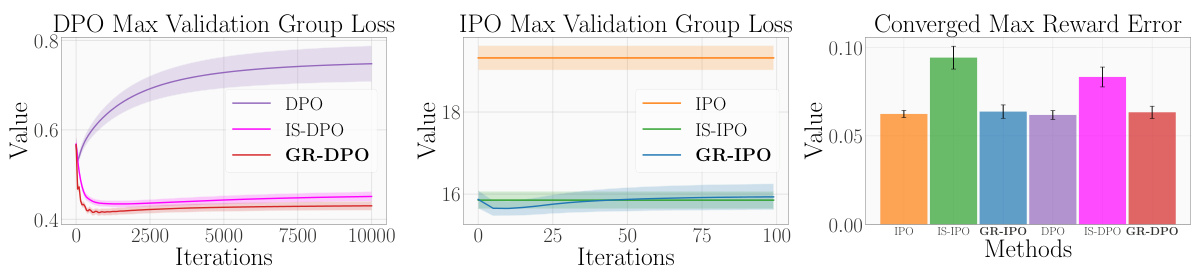
This figure presents the results of synthetic experiments comparing the performance of the proposed GRPO algorithm (GR-DPO and GR-IPO) against standard DPO and IPO methods, as well as importance sampling (IS) variants. The results show that GRPO consistently achieves a lower worst-case validation loss and reward error across different scenarios, especially when group sizes and response distributions vary. The x-axis represents training iterations and the y-axis shows the loss or error metrics.

This figure displays the results of synthetic experiments comparing Algorithm 1 (GR-DPO and GR-IPO) against standard DPO and IPO methods, as well as importance sampling versions. It shows that Algorithm 1 significantly reduces both worst-case validation loss and reward error. The specific scenario shown involves groups with differing sizes and response distributions, demonstrating the algorithm’s robustness to these variations.

This figure presents the results of synthetic experiments comparing different preference optimization methods. Algorithm 1, a novel group robust preference optimization method (GRPO), shows significantly lower worst-case validation loss and reward error than importance sampling (IS) versions of DPO and IPO, as well as the standard DPO and IPO methods. The experiment specifically tests a scenario where groups have different sizes and response distributions, highlighting GRPO’s robustness in diverse group settings.

This figure presents the results of synthetic experiments comparing the performance of the proposed GRPO algorithm (GR-DPO and GR-IPO) with several baselines (DPO, IPO, IS-DPO, IS-IPO). The experiments were conducted under a scenario where groups had different sizes and response distributions. The results show that GRPO significantly outperformed other methods in terms of both worst-case validation loss and reward error, demonstrating its effectiveness in handling imbalanced group sizes and diverse response distributions.

This figure presents results from synthetic experiments comparing the performance of the proposed GRPO algorithm (GR-DPO and GR-IPO) against standard DPO and IPO methods, as well as importance sampling versions. The results show that GRPO significantly reduces the maximum validation group loss and reward error across different experimental scenarios, particularly when group sizes and response distributions vary.

This figure displays the results of synthetic experiments comparing the performance of four algorithms: Algorithm 1 (GR-DPO and GR-IPO), Importance Sampling (IS-DPO/IPO), and vanilla DPO and IPO methods. The experiment simulates scenarios with varying group sizes and response distributions. The plots illustrate that Algorithm 1 consistently achieves lower worst-case validation group loss and reward error, showcasing its robustness in handling diverse group characteristics.

This figure displays the results of the Global Opinion experiments, comparing GR-IPO and IPO. The top plots show that GR-IPO achieves lower maximum group loss and higher minimum reward accuracy. The bottom plots illustrate the evolution of the log probability accuracy, group weights during training, and initial log probability accuracies. GR-IPO successfully addresses the performance imbalance across groups by adaptively weighting group losses during training.

Full paper

#