↗ arXiv ↗ Hugging Face ↗ Hugging Face ↗ Chat
TL;DR#
Large-scale pretrained models like Transformers, while effective, suffer from quadratic complexity in sequence length. This limits their applicability to longer sequences. Recent alternatives like structured state space models (SSMs) offer linear time complexity, but are primarily causal (unidirectional). This paper addresses the limitations of existing approaches by introducing a unifying matrix mixer framework.
The framework identifies key properties of matrix parameterizations that influence model efficiency and expressivity, including the novel concept of “sequence alignment.” Leveraging this framework, the researchers develop Hydra, a bidirectional extension of the Mamba model (an SSM), parameterized as a quasiseparable matrix mixer. Hydra shows superior performance over existing models including Transformers, especially on non-causal tasks, demonstrating its potential as a drop-in replacement for attention layers.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with sequence models because it offers a unifying framework for understanding various existing models and developing new ones with desirable properties. The introduction of sequence alignment and the proposal of Hydra, a bidirectional model, significantly advance the field and open avenues for further research in efficient and expressive sequence modeling. The demonstrated superior performance of Hydra on benchmark datasets highlights its practical value and potential to impact various applications.
Visual Insights#

🔼 The figure is divided into two parts. The left part shows a schematic of the matrix mixer framework. It illustrates how an input sequence X is preprocessed using a function fx, then passed through a sequence mixer (represented by a matrix M), and finally processed by a channel mixer to produce the output sequence Y. The right part provides an overview of different classes of structured matrices that can be used as sequence mixers. These include dense, Vandermonde, Toeplitz, low-rank, semiseparable, and quasiseparable matrices. Each matrix type is visually represented along with a formula to better demonstrate the key differences between the classes of matrices. This part also highlights the different properties of each matrix that makes it suitable for use in the model.
read the caption
Figure 1: (Left) A schematic of the matrix mixer framework. (Right) An overview of matrix mixer classes: dense, Vandermonde, Toeplitz, low-rank, semiseparable, and quasiseparable.
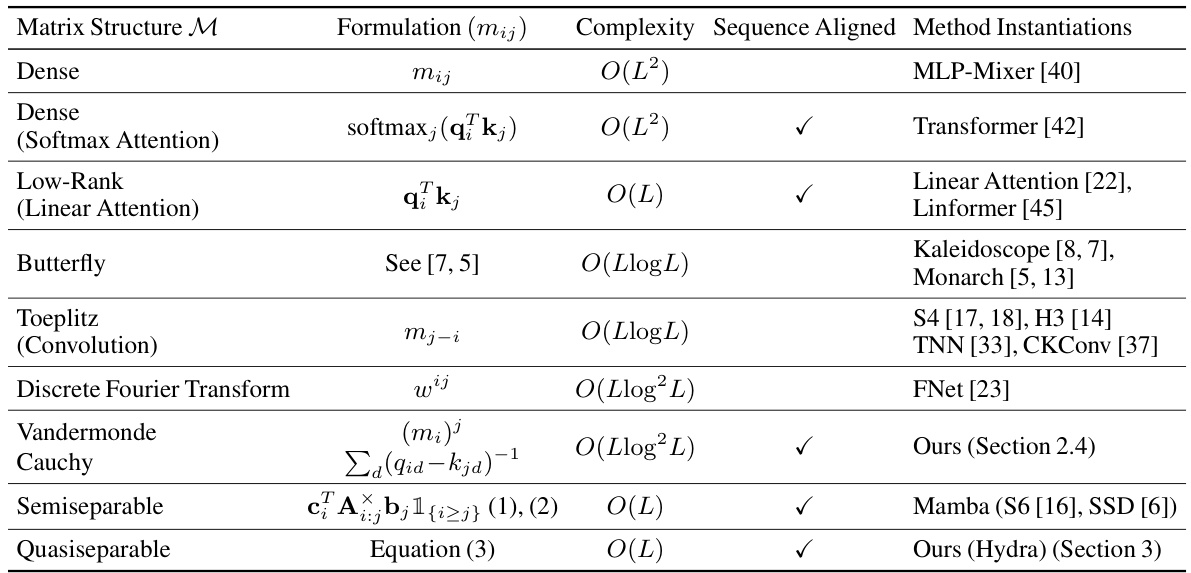
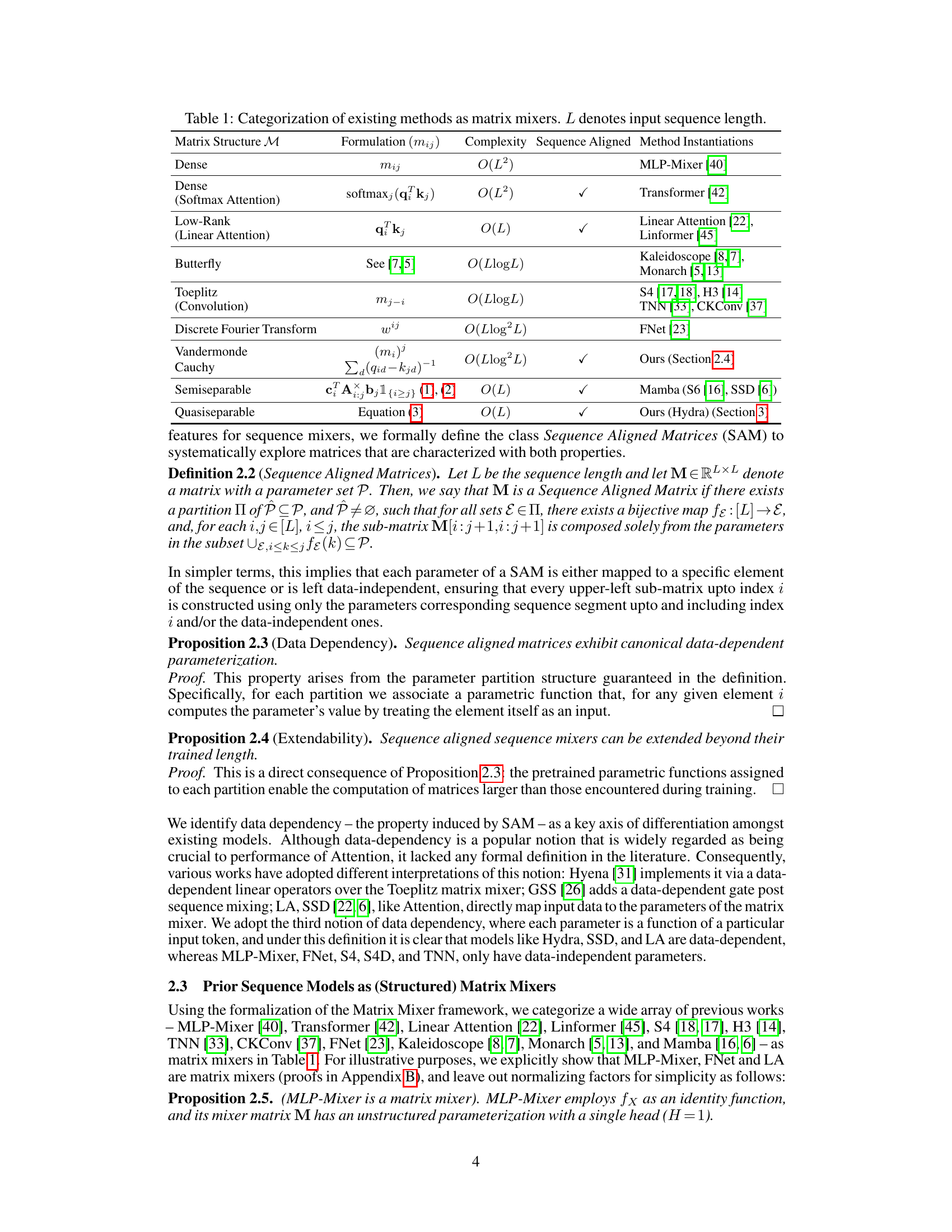
🔼 This table categorizes various existing sequence models based on their underlying matrix mixer structures. It shows the type of matrix used (e.g., dense, low-rank, Toeplitz), the computational complexity of the matrix multiplication, whether the matrix is sequence aligned (meaning the matrix parameters are data-dependent), and specific examples of models that utilize each type of matrix. The table highlights the key properties that affect the efficiency and expressiveness of different sequence models.
read the caption
Table 1: Categorization of existing methods as matrix mixers. L denotes input sequence length.
In-depth insights#
Matrix Mixer Models#
Matrix mixer models offer a novel perspective on sequence modeling, unifying diverse approaches under a common framework. They represent sequence mixing as linear transformations using various structured matrices, moving beyond the quadratic complexity of traditional attention mechanisms. This framework enables analysis of model efficiency and expressivity through the properties of their matrix classes, highlighting the importance of sequence alignment for improved performance. The ability to systematically design new models with desired properties makes this approach particularly valuable, leading to the development of novel sub-quadratic sequence models like Hydra. By exploring different matrix types, such as quasiseparable matrices, we can better understand the strengths and limitations of various sequence modeling techniques and design more efficient and effective models for various tasks.
Sequence Alignment#
The concept of ‘Sequence Alignment’ introduced in the paper offers a novel perspective on structuring matrix operations within sequence models. It’s presented as a crucial property influencing model characteristics like data dependency and extendability. Sequence Aligned Matrices (SAMs) are defined based on this concept, highlighting a key difference between various matrix-based sequence models. Data dependency, enabled by SAMs, ensures that matrix parameters dynamically adapt to the input sequence, leading to improved performance. Extendability allows SAM-based models to easily handle sequences longer than those seen during training. The paper argues that this ‘Sequence Alignment’ is essential for the success of models like Transformers and recent SSMs, suggesting a unifying framework for analyzing and designing efficient and expressive sequence models.
Hydra: Bidirectional SSM#
The heading “Hydra: Bidirectional SSM” suggests a novel approach to state-space models (SSMs). Traditional SSMs often operate unidirectionally, limiting their applicability. Hydra likely addresses this limitation by introducing bidirectionality, enabling processing of sequential data in both forward and backward directions, thus enhancing model expressiveness and potentially improving performance on tasks where non-causal relationships matter. The name “Hydra” itself, alluding to the multi-headed serpent of Greek mythology, hints at a potentially multi-headed architecture within the SSM framework. This could involve multiple independent SSMs processing the data concurrently or sequentially, potentially using different parameterizations or inductive biases for each “head.” The bidirectionality combined with a multi-headed structure would allow Hydra to capture richer contextual information than traditional SSMs. This would be particularly relevant to tasks like natural language understanding and machine translation, where understanding both preceding and following contexts is crucial for accurate prediction.
Empirical Validation#
An Empirical Validation section would thoroughly investigate the claims made in a research paper. It would involve a detailed description of the experimental setup, datasets used, and evaluation metrics. Rigorous statistical analysis of results would be crucial, including error bars and significance testing to demonstrate the reliability of findings. The choice of baseline methods for comparison would be justified and the chosen baselines would be appropriately described. Ablation studies, systematically varying aspects of the proposed method, would highlight the contribution of specific components. The section’s strength depends on its clarity, completeness, and ability to convincingly support the paper’s core claims. The inclusion of a discussion about potential limitations, unexpected results, and any observed biases would further strengthen this section and exhibit a high level of research rigor. Finally, reproducibility is key; sufficient details should be provided to allow others to replicate the experiments.
Limitations & Future#
A research paper’s “Limitations & Future” section should critically examine shortcomings. Computational cost is a common limitation; many efficient models still fall short of Transformers’ performance. The section needs to address this, possibly suggesting future research into novel algorithms. Data dependence is another point to investigate; while beneficial, understanding how this affects generalization across various datasets is important. The section should also acknowledge limitations in the scope of experiments, and propose future work to address them such as testing on more diverse datasets and tasks. Finally, the paper should discuss any theoretical limitations in expressivity, proposing future work to improve model capacity and better handle longer sequences. The “Future” aspect should offer concrete steps for improving upon the presented work, including suggestions for specific research directions. Extending the models to handle various modalities, such as audio and video, and scaling to even larger datasets are valuable suggestions.
More visual insights#
More on figures
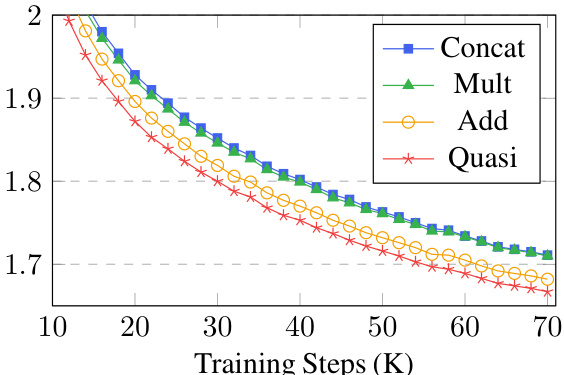
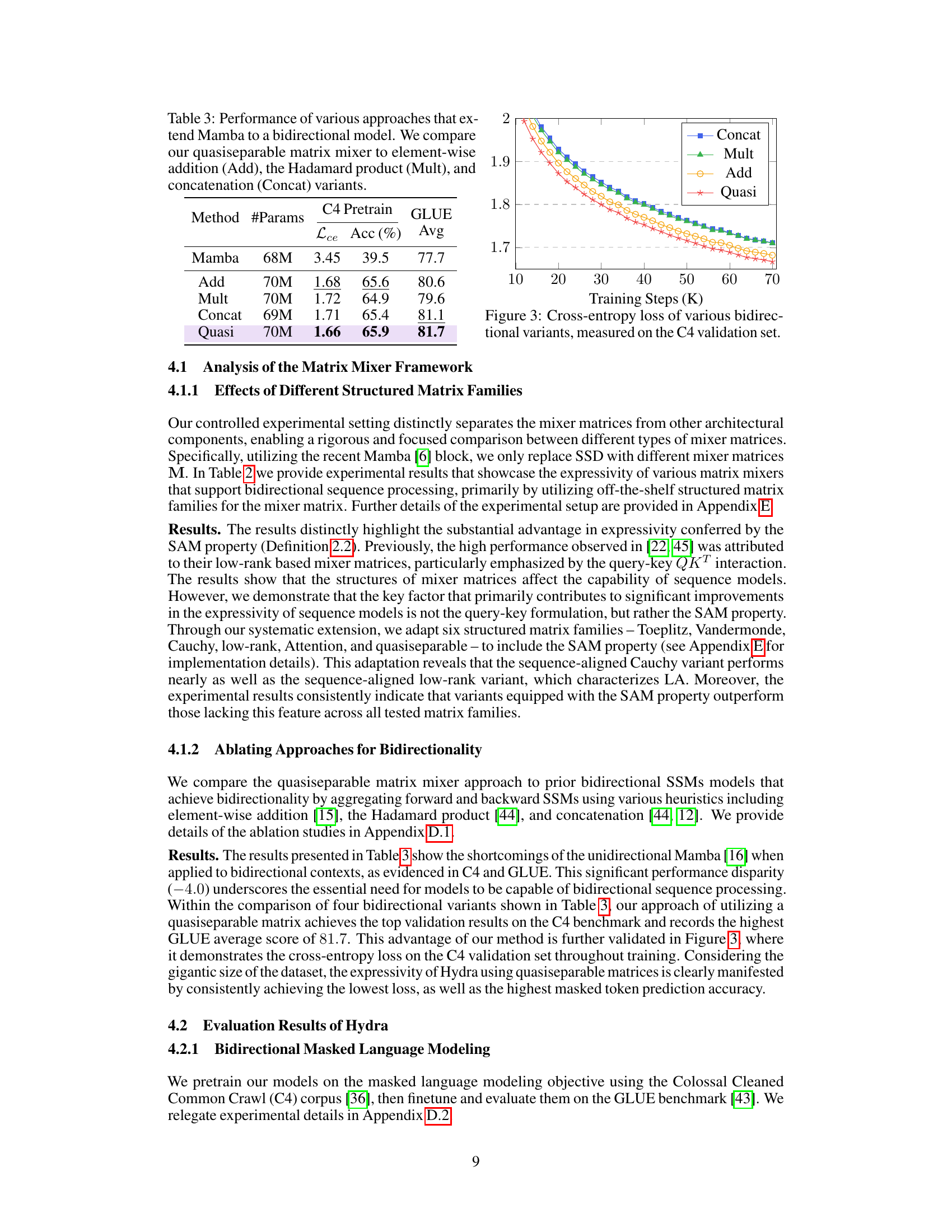
🔼 This figure shows the cross-entropy loss curves during training on the C4 validation set for different methods of creating bidirectional sequence models. The methods compared are concatenation (Concat), Hadamard product (Mult), element-wise addition (Add), and the proposed quasiseparable matrix mixer (Quasi). The plot demonstrates the training progress over 70,000 steps, illustrating how the loss decreases over time for each method. The quasiseparable method shows a consistently lower loss than other approaches. This visual comparison underscores Hydra’s superior performance in bidirectional sequence modeling.
read the caption
Figure 3: Cross-entropy loss of various bidirectional variants, measured on the C4 validation set.
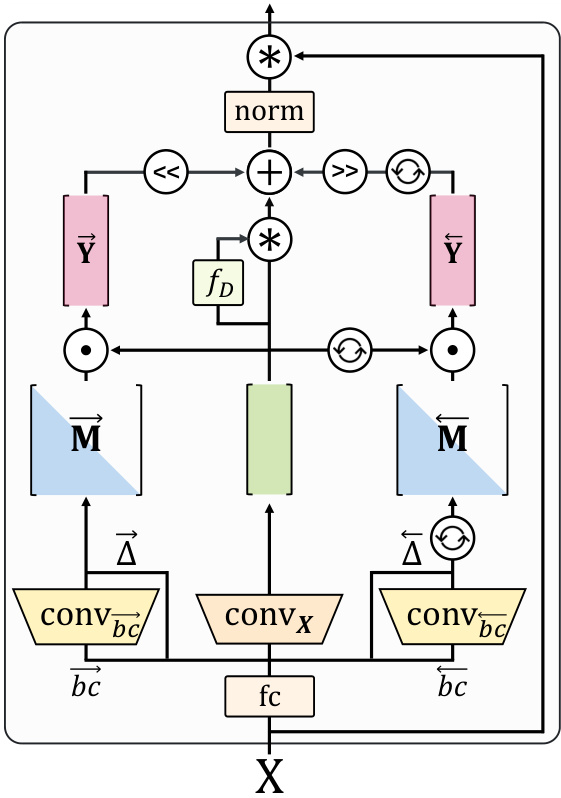
🔼 This figure provides a detailed illustration of the architecture of the Hydra model. It shows the flow of data through various components, including the forward and backward passes. Each component is labeled and the connections are clearly shown. The figure helps visualize the overall structure and operation of the Hydra model. The components include convolutions, matrix multiplications, non-linearities, and normalization.
read the caption
Figure 4: Detailed illustration of Hydra.

🔼 This figure illustrates the matrix structures of semiseparable (SS), quasiseparable (QS) matrices, and how they relate to the Hydra model. It highlights the rank properties that distinguish SS and QS matrices, showing how QS matrices generalize SS matrices and a common bidirectional SSM approach. The key takeaway is that Hydra’s QS matrix structure provides greater expressivity than simpler addition-based bidirectional SSMs due to its unconstrained diagonal values.
read the caption
Figure 2: (a) A semiseparable (SS) matrix. (b) A quasiseparable (QS) matrix. (c) A mixer matrix of addition-based bidirectional SSMs. (d) A QS mixer matrix for Hydra. SS and QS matrices are characterized by rank conditions (Definition 3.1, Definition 3.2). The rank characterization of SS matrices include the diagonals (e.g., green submatrices), whereas that of QS matrices hold for off-diagonal submatrices (e.g., yellow submatrices). Because of the similar rank properties, a naive addition-based bidirectional SSM is provably a QS matrix mixer. Hence, QS matrix mixers generalize this common heuristic for bidirectional SSMs. The freedom in the diagonal values of Hydra leads to a higher expressivity compared to the mixer matrices of the addition-based bidirectional SSMs, where the diagonal values are constrained by the colored vectors.
More on tables

🔼 This table presents the results of an ablation study comparing various matrix mixer types on the GLUE benchmark. The study controls for architectural differences, focusing solely on the impact of different matrix parameterizations. Key findings highlight the significant performance boost achieved by using sequence-aligned matrices (which dynamically adjust parameters based on input projections), making them data-dependent.
read the caption
Table 2: Matrix mixer ablations. A systematic empirical study of matrix mixers on the GLUE benchmark by controlling for the architecture and varying only the matrix parameterization. Sequence-aligned matrices dynamically parameterize via input projections, becoming data-dependent (DD) that significantly increases performance. Most DD variants achieve competitive GLUE scores.
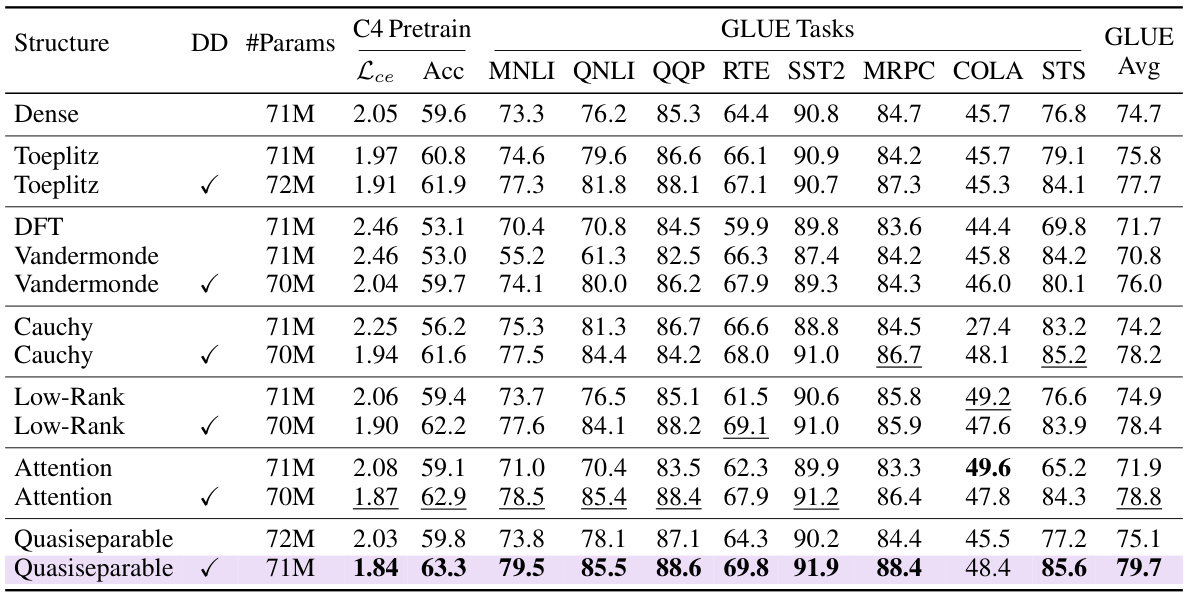
🔼 This table presents the results of an ablation study comparing various matrix mixer types on the GLUE benchmark. The study controls for architectural differences, varying only the matrix parameterization to isolate its impact on performance. The results show that sequence-aligned matrices, which dynamically adapt their parameters based on input data, significantly improve performance compared to their data-independent counterparts.
read the caption
Table 2: Matrix mixer ablations. A systematic empirical study of matrix mixers on the GLUE benchmark by controlling for the architecture and varying only the matrix parameterization. Sequence-aligned matrices dynamically parameterize via input projections, becoming data-dependent (DD) that significantly increases performance. Most DD variants achieve competitive GLUE scores.
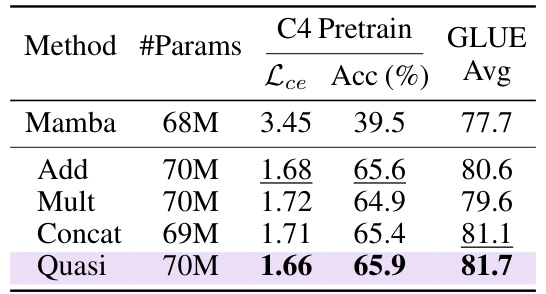
🔼 This table compares different methods for extending the Mamba model to handle bidirectional sequences. It contrasts the performance of a quasiseparable matrix mixer (the proposed Hydra model) against three simpler approaches: element-wise addition, Hadamard product, and concatenation. The comparison is done in terms of cross-entropy loss (Lce) during pretraining on the C4 dataset and the average GLUE score achieved after fine-tuning.
read the caption
Table 3: Performance of various approaches that extend Mamba to a bidirectional model. We compare our quasiseparable matrix mixer to element-wise addition (Add), the Hadamard product (Mult), and concatenation (Concat) variants.
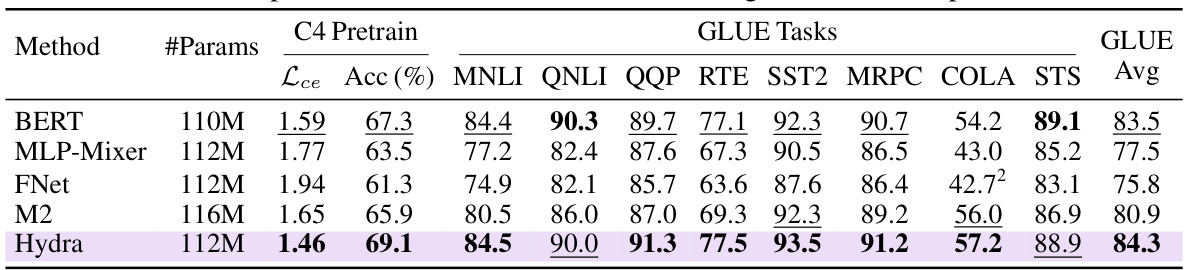
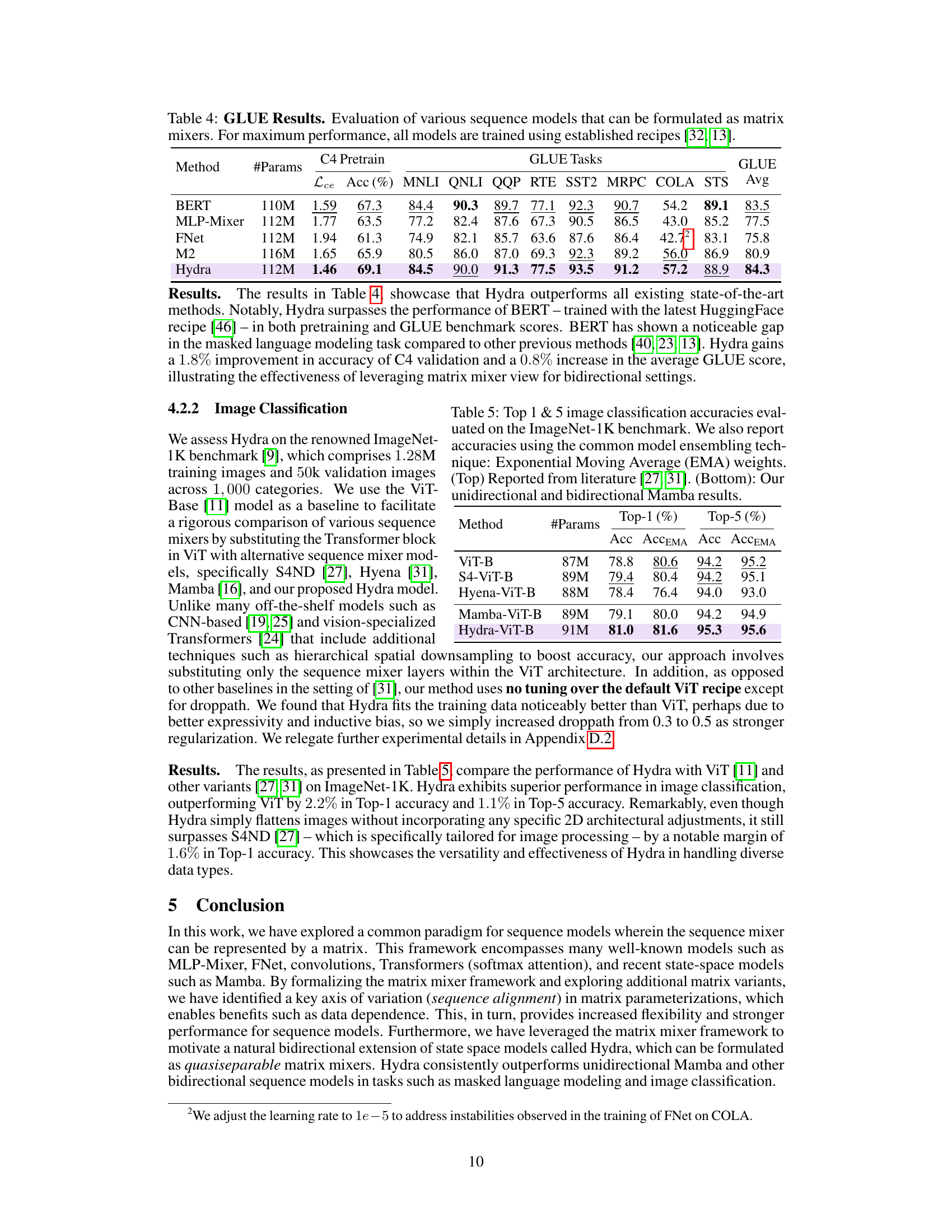
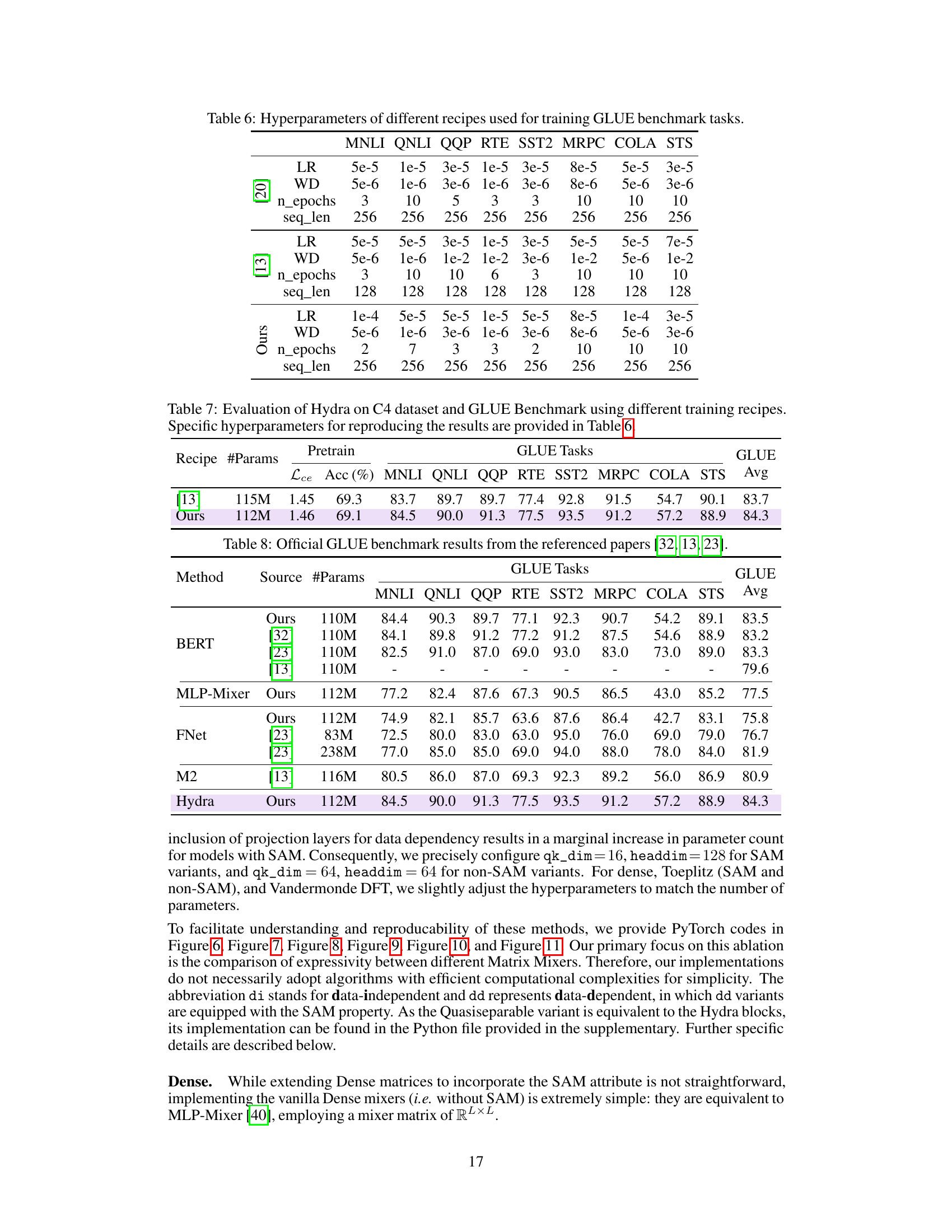
🔼 This table presents the GLUE benchmark results for various sequence models, including BERT, MLP-Mixer, FNet, M2, and the proposed Hydra model. All models were trained using established training recipes for optimal performance. The table shows the performance metrics (accuracy and cross-entropy loss) for each model on the different GLUE subtasks and the overall GLUE average score.
read the caption
Table 4: GLUE Results. Evaluation of various sequence models that can be formulated as matrix mixers. For maximum performance, all models are trained using established recipes [32, 13].
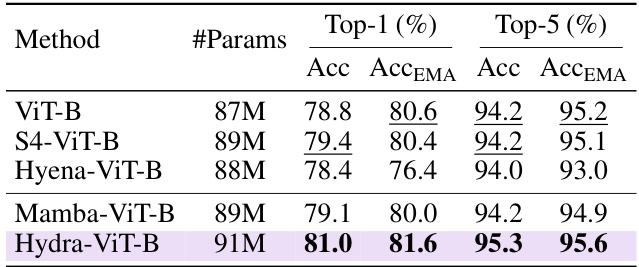
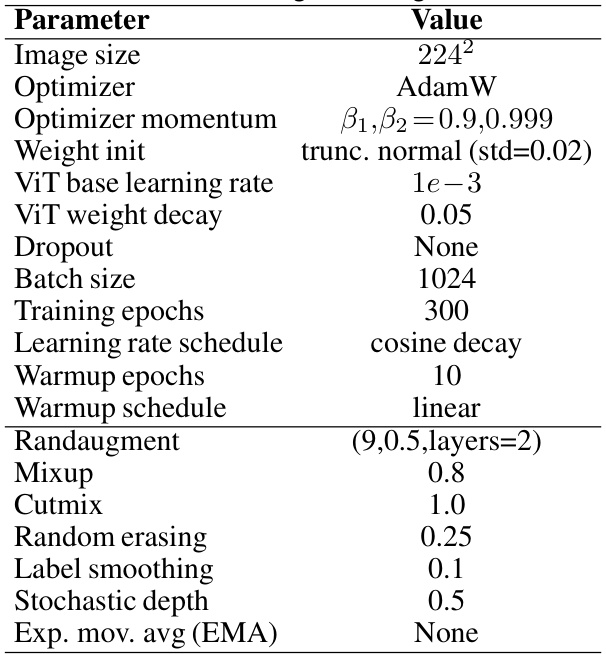
🔼 This table presents the top-1 and top-5 accuracies achieved by different models on the ImageNet-1K image classification benchmark. It compares the performance of Hydra against several other state-of-the-art models, including ViT-B, S4-ViT-B, Hyena-ViT-B, and Mamba-ViT-B. Results are shown with and without exponential moving average (EMA) ensembling for a more comprehensive comparison.
read the caption
Table 5: Top 1 & 5 image classification accuracies evaluated on the ImageNet-1K benchmark. We also report accuracies using the common model ensembling technique: Exponential Moving Average (EMA) weights. (Top) Reported from literature [27, 31]. (Bottom): Our unidirectional and bidirectional Mamba results.

🔼 This table presents the results of an ablation study comparing various matrix mixer architectures on the GLUE benchmark. The study controls for architectural differences, focusing solely on the impact of different matrix parameterizations. The results show that sequence-aligned matrices, which dynamically adjust their parameters based on the input, significantly improve performance.
read the caption
Table 2: Matrix mixer ablations. A systematic empirical study of matrix mixers on the GLUE benchmark by controlling for the architecture and varying only the matrix parameterization. Sequence-aligned matrices dynamically parameterize via input projections, becoming data-dependent (DD) that significantly increases performance. Most DD variants achieve competitive GLUE scores.
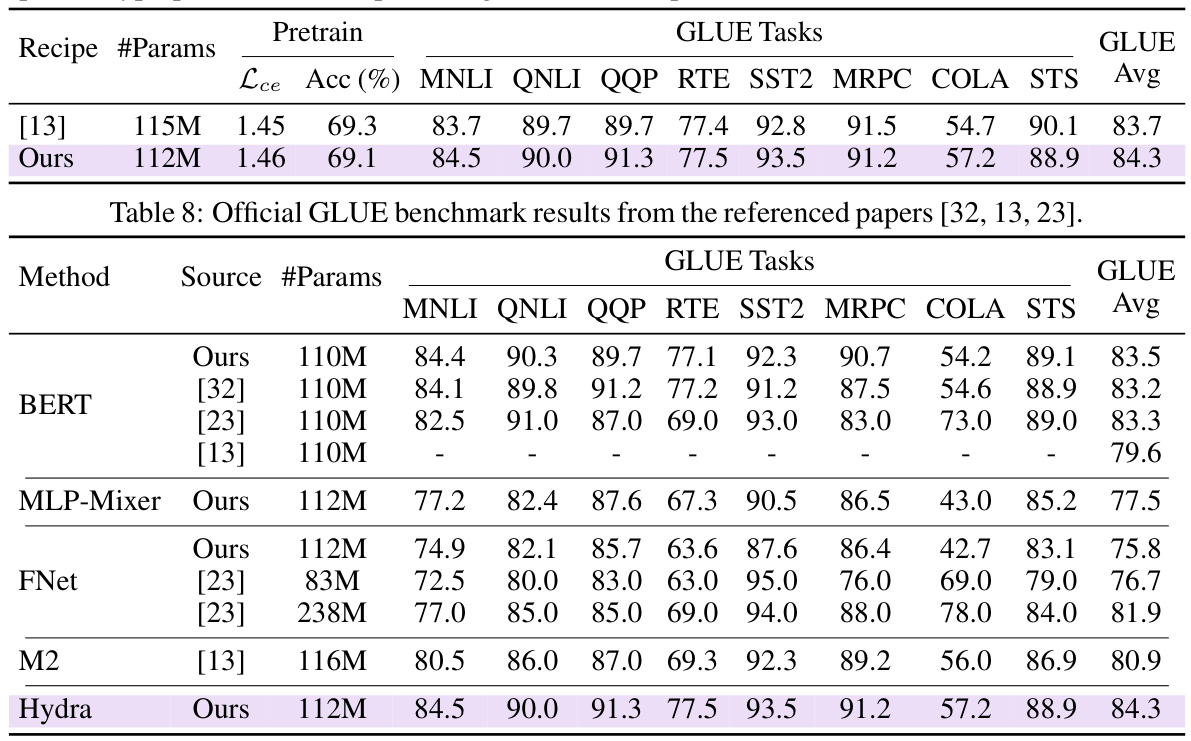
🔼 This table presents the results of an ablation study comparing different types of matrix mixers on the GLUE benchmark. The study controls for architectural differences to isolate the impact of the matrix parameterization. The results show that sequence-aligned matrices, which dynamically adjust their parameters based on the input data, significantly improve performance compared to their data-independent counterparts. Most of the data-dependent variants achieve competitive GLUE scores.
read the caption
Table 2: Matrix mixer ablations. A systematic empirical study of matrix mixers on the GLUE benchmark by controlling for the architecture and varying only the matrix parameterization. Sequence-aligned matrices dynamically parameterize via input projections, becoming data-dependent (DD) that significantly increases performance. Most DD variants achieve competitive GLUE scores.
🔼 This table presents the results of an ablation study on various matrix mixer architectures for natural language understanding. The study controls for architectural differences and isolates the impact of the matrix parameterization on the GLUE benchmark. It highlights the benefit of sequence alignment, a key property in dynamically parameterizing matrix mixers, resulting in improved performance. The table shows different matrix types, their parameter counts, and their performance across various GLUE sub-tasks.
read the caption
Table 2: Matrix mixer ablations. A systematic empirical study of matrix mixers on the GLUE benchmark by controlling for the architecture and varying only the matrix parameterization. Sequence-aligned matrices dynamically parameterize via input projections, becoming data-dependent (DD) that significantly increases performance. Most DD variants achieve competitive GLUE scores.
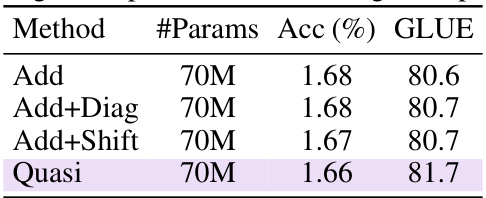
🔼 This table presents the results of an ablation study comparing different types of matrix mixers used in a sequence model on the GLUE benchmark. The study controls for architectural differences, varying only the matrix parameterization. The results show that sequence-aligned matrices, which dynamically adjust their parameters based on the input, significantly outperform non-sequence-aligned matrices. The table also highlights the generally competitive GLUE scores achieved by most of the data-dependent variants.
read the caption
Table 2: Matrix mixer ablations. A systematic empirical study of matrix mixers on the GLUE benchmark by controlling for the architecture and varying only the matrix parameterization. Sequence-aligned matrices dynamically parameterize via input projections, becoming data-dependent (DD) that significantly increases performance. Most DD variants achieve competitive GLUE scores.
Full paper#