Stochastic Kernel Regularisation Improves Generalisation in Deep Kernel Machines

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it significantly improves the generalization capabilities of deep kernel machines, a promising alternative to neural networks for complex tasks like image classification. The findings challenge the notion that superior performance on such tasks is exclusive to neural networks, opening new avenues for research and development in kernel methods and representation learning. The proposed stochastic kernel regularization technique is a novel and impactful contribution, offering a valuable tool for researchers working on kernel-based methods and deep learning.

Visual Insights

#

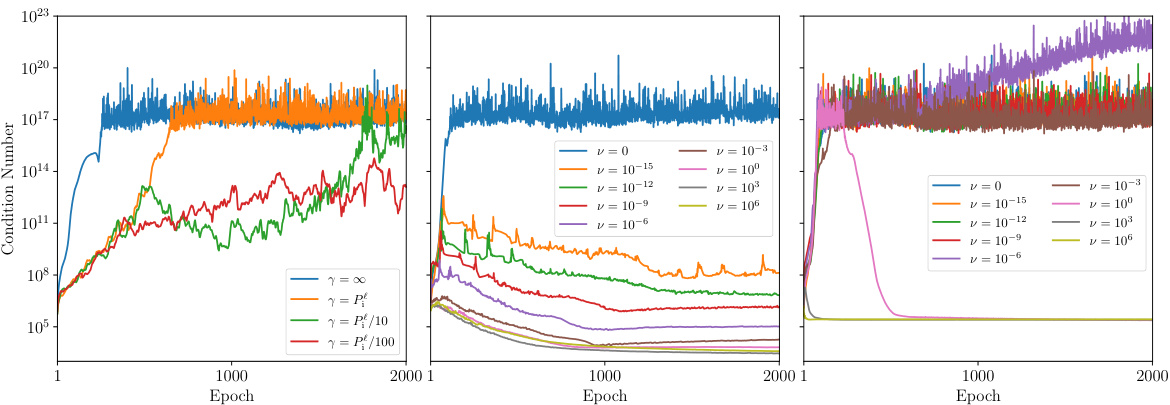
This figure displays the effects of different regularization methods on the condition number of Gram matrices in a toy binary classification problem. Three plots illustrate the impacts of stochastic kernel regularization (γ), the KL regularization coefficient (v) with and without Taylor approximation on the Gram matrix’s condition number over 2000 training epochs. The results show how these methods impact the stability of the Gram matrices during training.

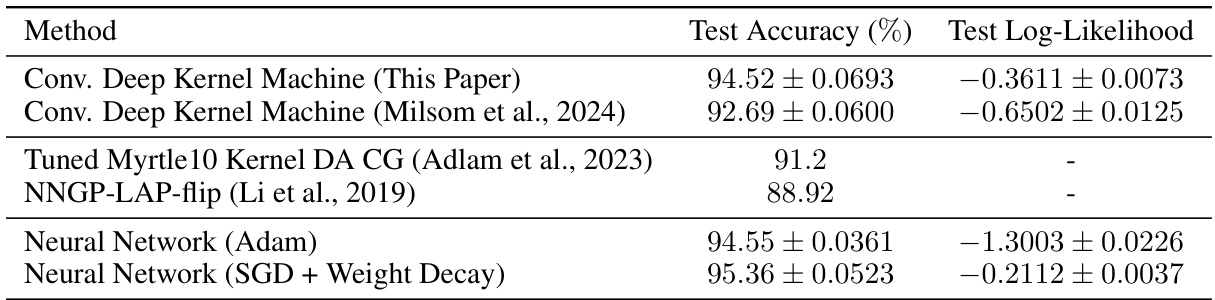
This table presents a comparison of test accuracy and test log-likelihood achieved by different methods on the CIFAR-10 dataset. The methods compared include a Convolutional Deep Kernel Machine (DKM) from this paper, a Convolutional Deep Kernel Machine from previous work (Milsom et al., 2024), and state-of-the-art methods based on tuned Myrtle10 Kernel and NNGP-LAP-flip, alongside a neural network trained with Adam and another with SGD+Weight Decay for comparison. The table shows that the proposed DKM in this paper achieves comparable performance to a Neural Network trained using Adam and outperforms previous methods.

In-depth insights

#

Deep Kernel Generalization

#

Deep kernel methods, while powerful, often struggle with generalization compared to neural networks. This limitation stems from the fixed nature of traditional kernel functions, hindering the ability to learn complex data representations. The concept of “Deep Kernel Generalization” focuses on enhancing the representational power of these methods. Strategies like stochastic kernel regularization, as explored in the provided paper, aim to overcome overfitting by introducing noise to the learned kernel matrices. This injection of randomness helps prevent the model from memorizing training data, improving its ability to generalize to unseen examples. Another significant aspect involves improving numerical stability, often crucial for training deep kernel machines using lower precision arithmetic. The effective use of inducing points dramatically reduces the computational burden, allowing for more extensive training. The success of this approach hinges on finding a balance between enhancing representational learning and maintaining numerical stability. Ultimately, Deep Kernel Generalization seeks to bridge the gap in generalization performance between deep kernel machines and deep neural networks, enabling kernel methods to tackle complex tasks such as image classification more effectively.

Stochastic Regularization

#

Stochastic regularization, in the context of deep kernel machines, addresses overfitting by introducing randomness during training. Instead of using deterministic Gram matrices, which represent learned representations, the method samples from a Wishart distribution. This injection of noise prevents the model from relying too heavily on specific features, thus improving generalization. The approach is particularly beneficial for convolutional deep kernel machines which are prone to overfitting. The method’s effectiveness is demonstrated by a notable increase in test accuracy on the CIFAR-10 dataset. The paper highlights that this stochastic regularisation acts as a powerful technique to improve the numerical stability of training in lower-precision arithmetic, speeding up computation while maintaining performance. However, the exploration is limited to one dataset (CIFAR-10) and it requires more extensive testing with different datasets and architectures before its benefits can be fully ascertained. Future research might also explore alternative noise distributions or more sophisticated sampling strategies to further refine this technique.

Low-Precision Training

#

Low-precision training, employing reduced-precision arithmetic (e.g., TF32 instead of FP64), offers significant speedups in deep learning. However, it introduces numerical instability challenges, particularly when dealing with ill-conditioned matrices commonly encountered in kernel methods. The paper addresses these challenges through two key strategies: First, stochastic kernel regularization (SKR) introduces controlled randomness during training to reduce overfitting and improve numerical stability. Second, a Taylor approximation of the log-determinant term in the objective function mitigates instability associated with low-precision matrix inversions. The combination of SKR and the Taylor approximation is crucial for enabling the use of low-precision arithmetic while maintaining accuracy. By using lower-precision computations, the training process accelerates significantly, making training more computationally affordable, and thus enabling additional epochs which improves performance. This approach allows for balancing speed against the need for sufficient precision for high-accuracy results.

Ablation Experiments

#

Ablation experiments systematically remove components of a model to assess their individual contributions. In this context, the researchers likely conducted several ablation studies on their convolutional deep kernel machine (DKM). Key components assessed might include stochastic kernel regularization (SKR), the Taylor approximation of the KL divergence term in the objective function, and the use of lower-precision (TF32) arithmetic. By selectively disabling these elements and measuring the resulting impact on performance metrics (test accuracy and log-likelihood), they quantified the importance of each modification. The results would highlight whether gains were additive or synergistic and reveal potential trade-offs between computational efficiency and model accuracy. Successful ablations would confirm the individual benefits of each proposed technique, strengthening the overall argument of the paper. Conversely, unexpected results might point to unforeseen interactions between the model components and suggest directions for future research.

Future DKM Research

#

Future research directions for Deep Kernel Machines (DKMs) are promising. Improving scalability beyond current O(P³) complexity is crucial for handling massive datasets. This could involve exploring more efficient kernel approximations or leveraging techniques like subsampling or low-rank approximations more effectively. Enhancing the expressiveness of DKMs is also key. While DKMs have shown impressive results, they still lag behind state-of-the-art neural networks in certain aspects. Investigating new kernel architectures, novel non-linearity functions, and advanced representation learning strategies could boost their performance. Addressing numerical stability issues when employing low-precision arithmetic, particularly crucial for large-scale training, is vital. Robust optimization techniques and regularization strategies specific to DKMs should be developed to achieve this. Finally, theoretical analysis remains an important focus. Bridging the gap between DKMs and the Neural Tangent Kernel (NTK) framework could provide valuable insights into their generalization capabilities and performance. Furthermore, exploring the connections between DKMs and other kernel methods, such as Gaussian Processes, could lead to advancements in both fields.

More visual insights

#

More on tables

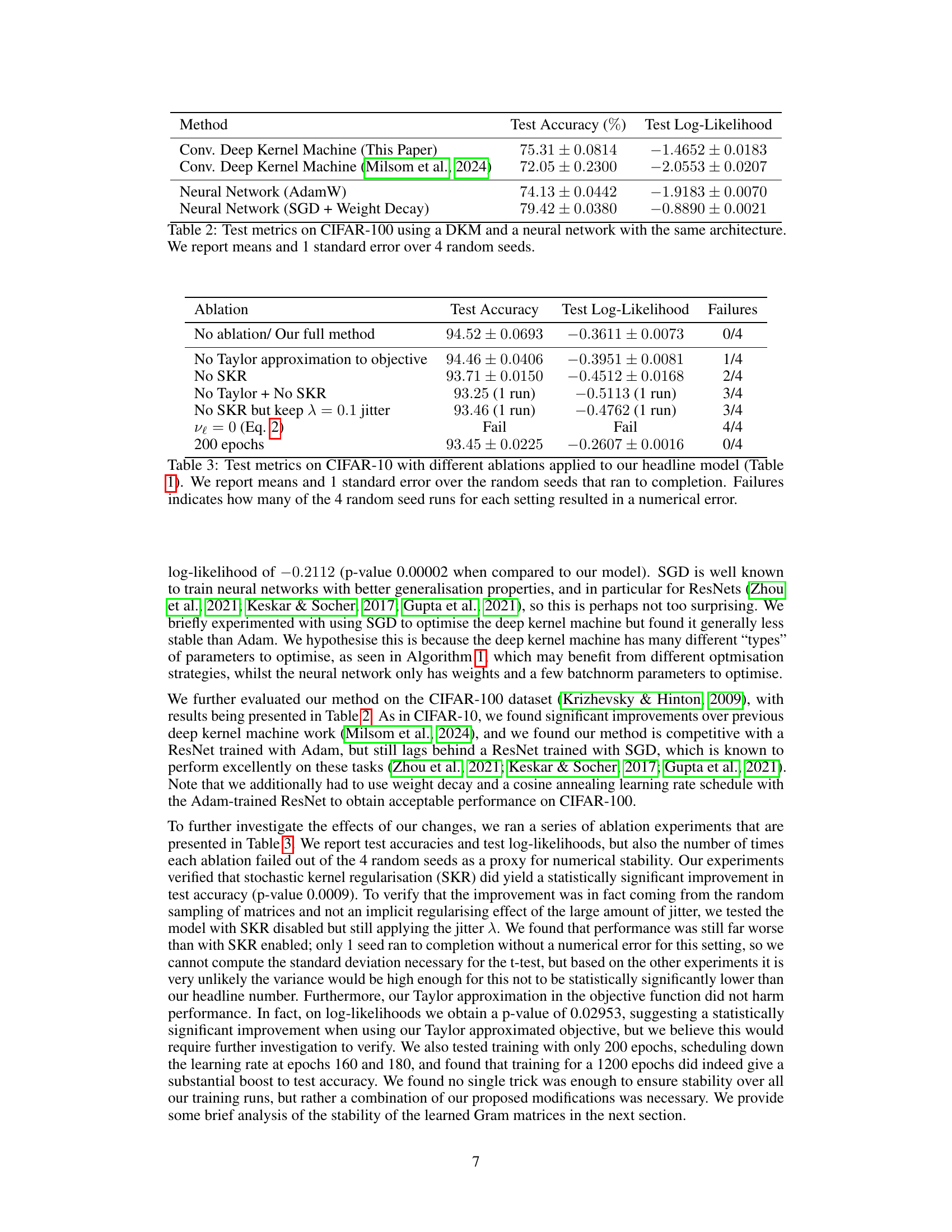
This table presents the results of experiments conducted on the CIFAR-100 dataset using both a Convolutional Deep Kernel Machine (DKM) and a neural network that share the same architecture. The table compares the test accuracy and test log-likelihood achieved by four different models: the proposed convolutional DKM, a convolutional DKM from prior work, a neural network trained with AdamW, and a neural network trained with SGD and weight decay. Each result represents the mean and standard error calculated from four independent runs with different random seeds. The data demonstrates the performance comparison of DKMs and neural networks on a challenging image classification task.

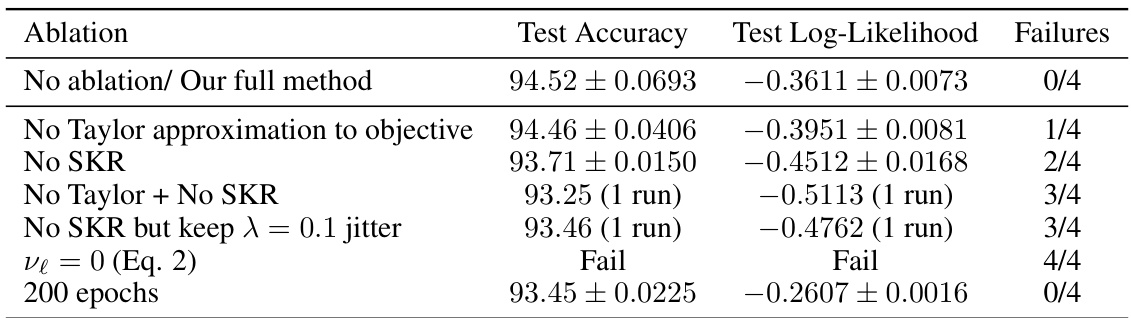
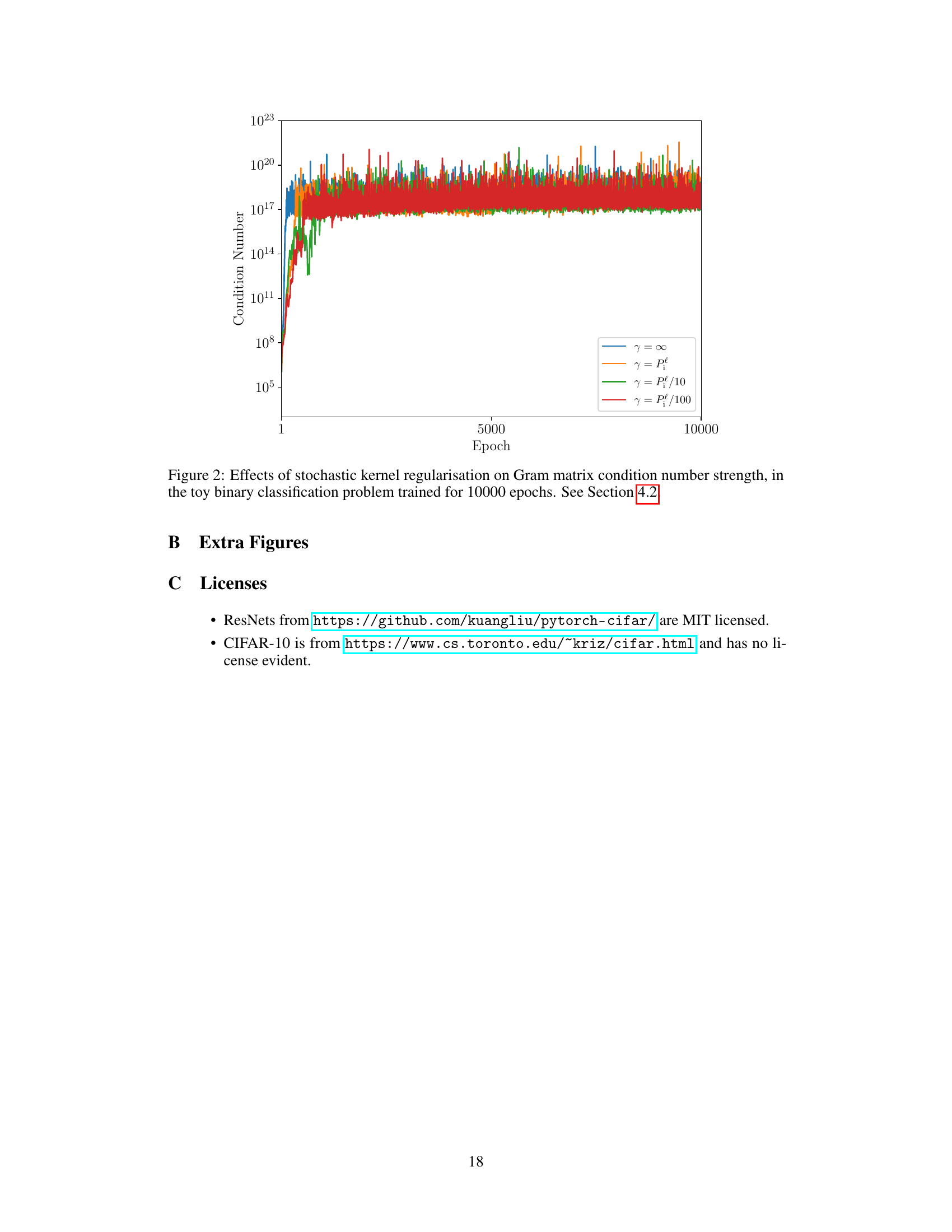
This table presents the ablation study of the proposed method on the CIFAR-10 dataset. It shows the impact of removing key components of the model, such as the Taylor approximation, stochastic kernel regularization (SKR), and the effect of reducing the number of training epochs. The test accuracy and log-likelihood are reported, along with the number of times each configuration resulted in a numerical error during training (Failures). This helps to assess the importance of each component to model performance and stability.

Full paper

#