↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Interactive teaching, where multiple models collaboratively refine each other, has shown promising results in machine learning but lacks theoretical understanding. Existing methods like co-teaching lack convergence analysis and are susceptible to getting stuck in local optima. This research addresses these limitations by: 1. providing a novel theoretical framework that casts co-teaching as an EM iterative process, showing how its convergence is achieved through continuous optimization of a variational lower bound; and 2. introducing SRIT, a new technique that integrates SAM (Sharpness-Aware Minimization) into interactive teaching to improve generalization performance and escape local optima.
SRIT enhances interactive teaching by incorporating SAM’s strength, resulting in a novel sequential optimization process. Experiments demonstrate that SRIT consistently improves model accuracy and generalization across multiple datasets and noise types compared to standard interactive teaching. The theoretical analysis explains the workings of the approach, while empirical validations showcase its effectiveness in various scenarios. This contributes a more robust and efficient strategy for interactive learning.
Key Takeaways#
Why does it matter?#
This paper is important because it offers a novel theoretical understanding of interactive teaching, a widely used technique in machine learning. It bridges the gap between empirical success and theoretical understanding, providing a new optimization framework (SRIT) that improves generalization and addresses issues like local optima. This work opens avenues for designing more effective and efficient interactive teaching methods and has implications for various machine learning applications.
Visual Insights#

This figure illustrates the iterative process of interactive teaching and its enhancement with Sharpness Reduction Interactive Teaching (SRIT). The loss landscape is represented as a 3D surface, showing how the landscape changes over iterations. Initially, the landscape is complex and has many sharp peaks (high loss values). As interactive teaching proceeds, both models (f and g) learn to focus on low-loss regions by selectively discarding high-loss data points, leading to a gradual flattening of the landscape. SRIT further refines this by incorporating gradient information into the exchange process, leading to even greater flattening and improved generalization.
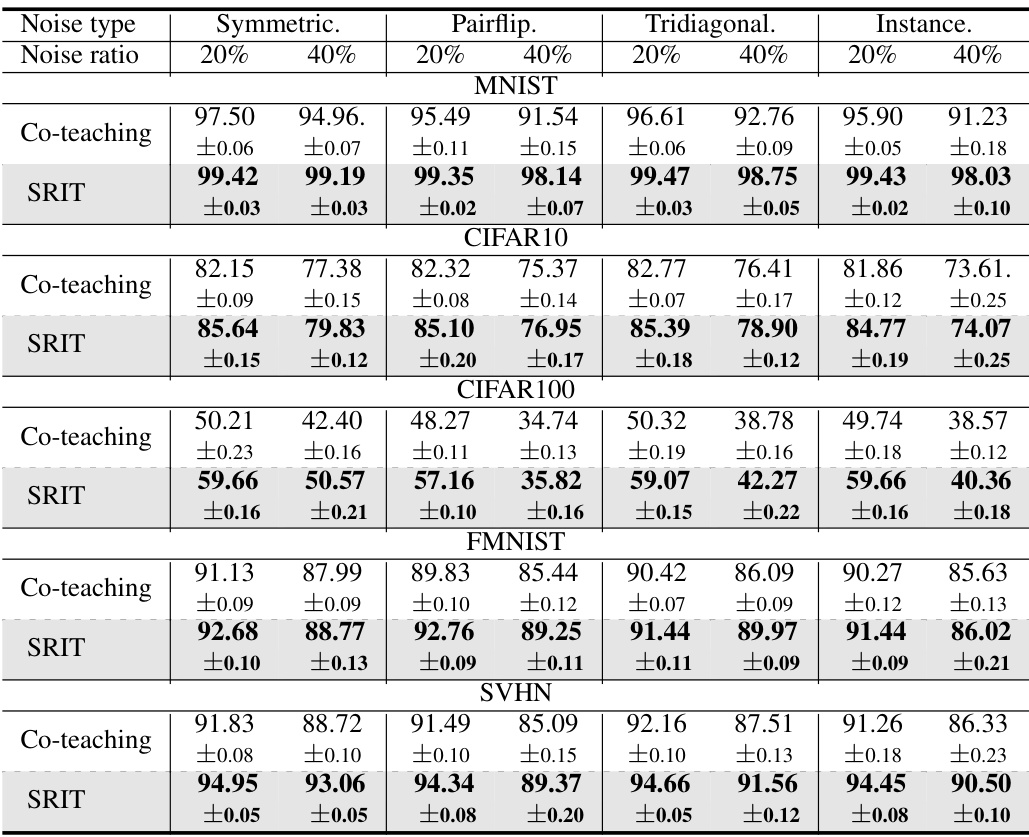
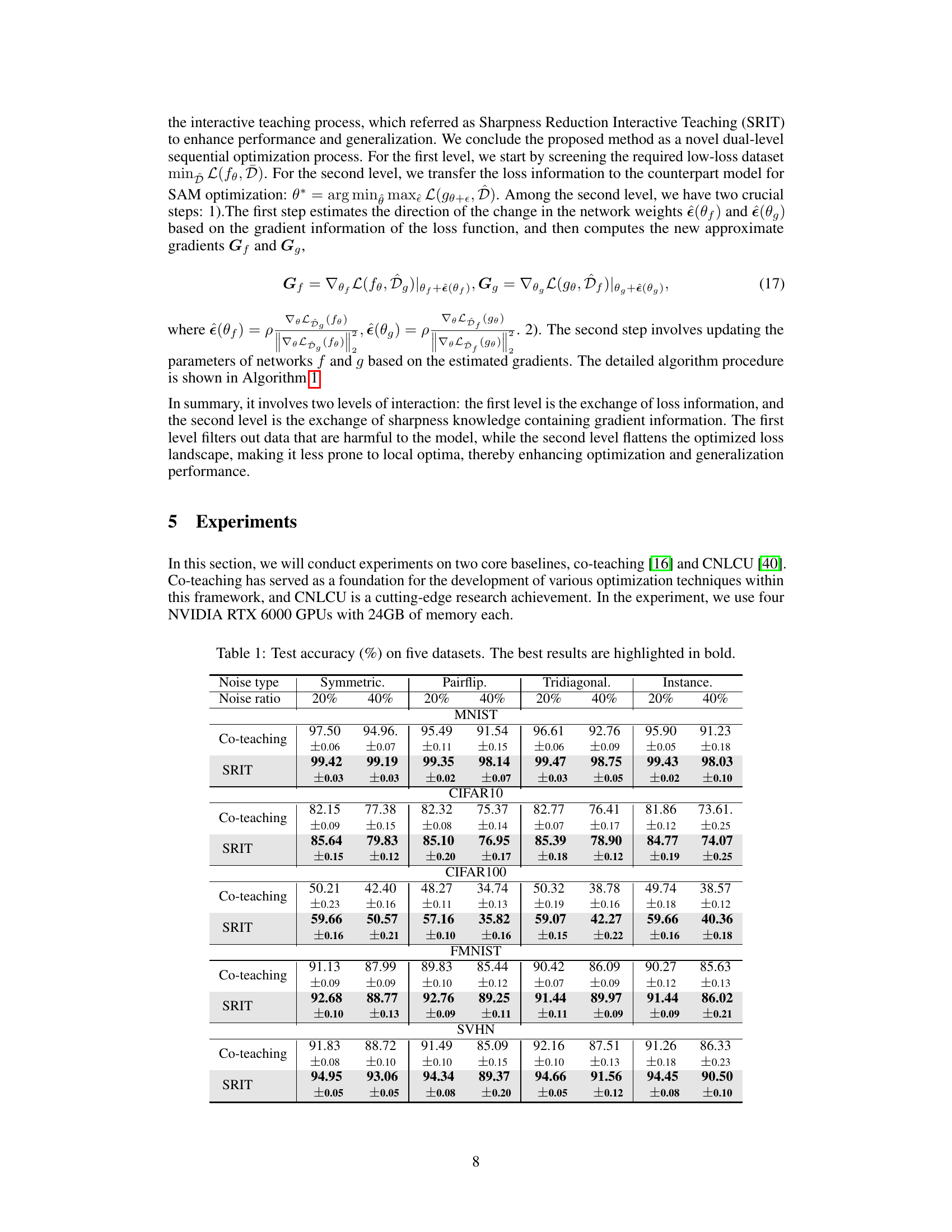
This table presents the test accuracy results for different noise types (Symmetric, Pairflip, Tridiagonal, Instance) and noise ratios (20%, 40%) across five datasets (MNIST, CIFAR10, CIFAR100, FMNIST, SVHN). The performance of two methods, Co-teaching and the proposed Sharpness Reduction Interactive Teaching (SRIT), are compared. The best accuracy for each condition is highlighted in bold, showcasing SRIT’s superior performance across various datasets and noise conditions.
In-depth insights#
Interactive Teaching#
The concept of “Interactive Teaching” in this research paper centers around the idea of using a collaborative learning paradigm, where multiple learning models (or agents) interact and teach each other. This contrasts with traditional, unidirectional teaching methods. The paper highlights co-teaching as a prime example, where two neural networks refine their parameters by selectively sharing samples with minimal losses, thereby guiding each other towards optimal performance. Sharpness-Aware Minimization (SAM) is integrated to enhance the process, ensuring that the models converge to flatter minima, thus improving generalization. The method’s convergence is theoretically analyzed using the Expectation-Maximization (EM) algorithm, and this framework lends a probabilistic interpretation to the interactive learning process. In essence, the interactive teaching paradigm is presented as a sequential optimization method with dual-level interactions, enhancing the learning efficiency, convergence, and generalization performance.
SAM Integration#
The integration of Sharpness-Aware Minimization (SAM) into interactive teaching methods represents a significant advancement. SAM’s strength lies in its ability to locate and favor flat minima in the loss landscape, improving generalization. By incorporating SAM, interactive teaching is not only enhanced in its ability to identify and utilize low-loss samples but also gains a mechanism to steer the learning process toward regions of improved generalization. This dual approach, combining the data selection of interactive teaching with the sharp minima avoidance of SAM, creates a synergistic effect. The resulting Sharpness Reduction Interactive Teaching (SRIT) method is particularly effective in noisy data scenarios where the original interactive methods might struggle. The combination suggests a novel sequential optimization approach, adding a layer of sharpness-aware refinement to the iterative process, potentially leading to faster convergence and robust solutions. However, the integration increases computational complexity, requiring careful consideration of computational costs when balancing the benefits of improved generalization and robustness against higher computational demands. Future research could investigate the optimal balance between these competing factors and explore more efficient implementations of the SAM integration.
Loss Landscape#
The concept of a loss landscape is crucial in understanding the optimization process of deep learning models. It provides a visual representation of the relationship between a model’s parameters and its loss function. Sharp minima, characterized by a steep drop in loss, are associated with poor generalization. Conversely, flat minima indicate robustness and better generalization performance. The paper investigates how the interactive teaching paradigm, specifically co-teaching, shapes this loss landscape. By iteratively selecting low-loss samples, interactive teaching effectively reduces the complexity of the loss landscape, leading to a smoother, flatter surface. This process facilitates easier convergence towards a more desirable minimum. Sharpness-Aware Minimization (SAM), a technique focused on finding flatter minima, is integrated to enhance the effectiveness of interactive teaching. SAM’s incorporation leads to what the authors term Sharpness Reduction Interactive Teaching (SRIT), a novel approach that combines the benefits of both paradigms. SRIT demonstrates improved generalization capabilities through experimental validation.
EM Algorithm#
The Expectation-Maximization (EM) algorithm is a powerful iterative method for finding maximum likelihood estimates of parameters in statistical models, especially when dealing with latent variables. The core idea is to iteratively refine estimates of both the parameters and the latent variables. In the E-step, the algorithm computes the expected value of the latent variables given the observed data and the current parameter estimates. This expectation step leverages existing knowledge to improve subsequent iterations. Then, in the M-step, the algorithm maximizes the likelihood function by updating the parameter estimates based on the expected values of the latent variables. This cyclical process of computing expectations and maximizing likelihood continues until convergence, ideally reaching a maximum likelihood solution. The EM algorithm’s strength lies in its ability to handle complex models with unobserved variables effectively, making it particularly useful in situations where direct maximization is intractable. However, a major limitation is the algorithm’s tendency to get stuck in local optima, requiring careful initialization and potentially multiple runs to find the global maximum. Furthermore, the computational cost of each EM iteration can be substantial, particularly in high-dimensional problems.
Future Research#
Future research directions stemming from this work on sharpness-aware minimization and interactive teaching could explore several promising avenues. Firstly, a more in-depth theoretical analysis could investigate the convergence rates of the proposed Sharpness Reduction Interactive Teaching (SRIT) algorithm under various noise conditions and data distributions. Secondly, the robustness of SRIT to different hyperparameter settings and its scalability to larger datasets and more complex models warrant further investigation. Thirdly, extending SRIT to other machine learning paradigms beyond deep learning, such as reinforcement learning or graph neural networks, could unlock new applications and reveal interesting insights. Finally, and perhaps most importantly, exploring the practical implications of SRIT in real-world educational settings would be crucial. This could involve designing user studies to evaluate SRIT’s effectiveness in improving human learning and understanding, potentially leading to new pedagogical approaches informed by the principles of sharpness-aware learning.
More visual insights#
More on figures

This figure is a 3D plot showing a loss landscape. The landscape is a complex, multi-peaked surface representing the loss function of a model across different parameter settings (x and y axes). A flat plane, the ‘cutting plane’, intersects the landscape. The cutting plane cuts off the high loss regions in each iteration. The caption indicates that the process iteratively removes regions of high loss, shaping the loss landscape to be more desirable for training.

This figure illustrates the iterative optimization process of interactive teaching and SRIT methods on the loss landscape. The plane represents the loss landscape. Interactive teaching methods iteratively update parameters, leading to a flatter loss landscape. SRIT further enhances this by incorporating gradient information, resulting in even greater flatness.
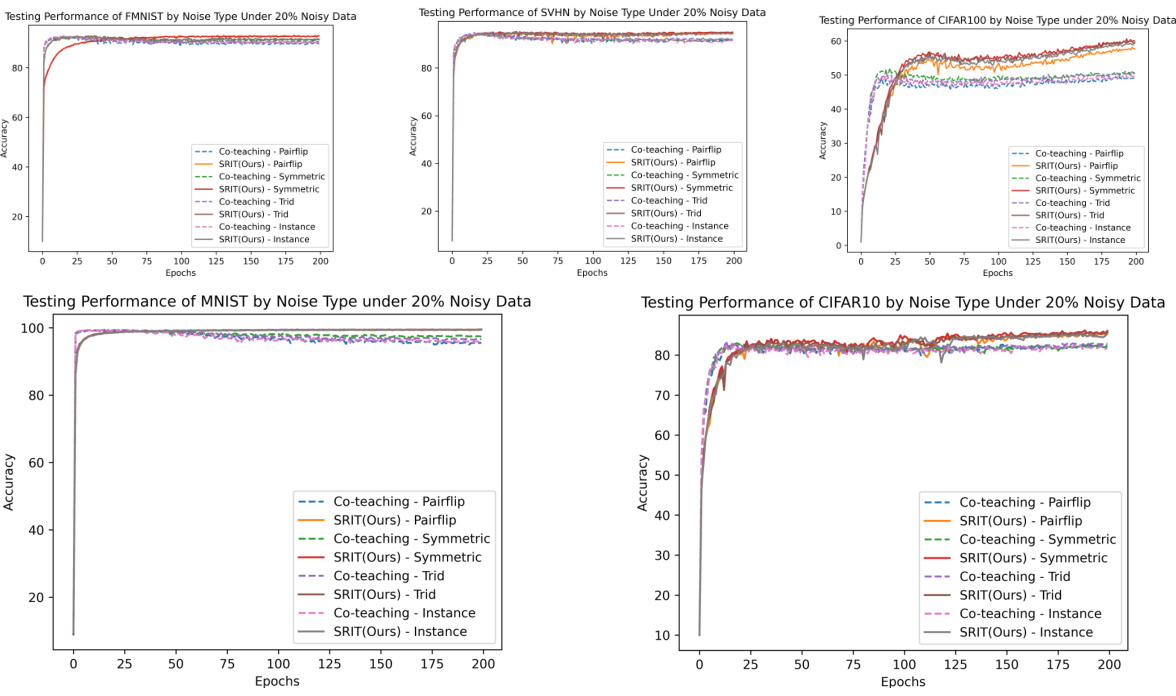
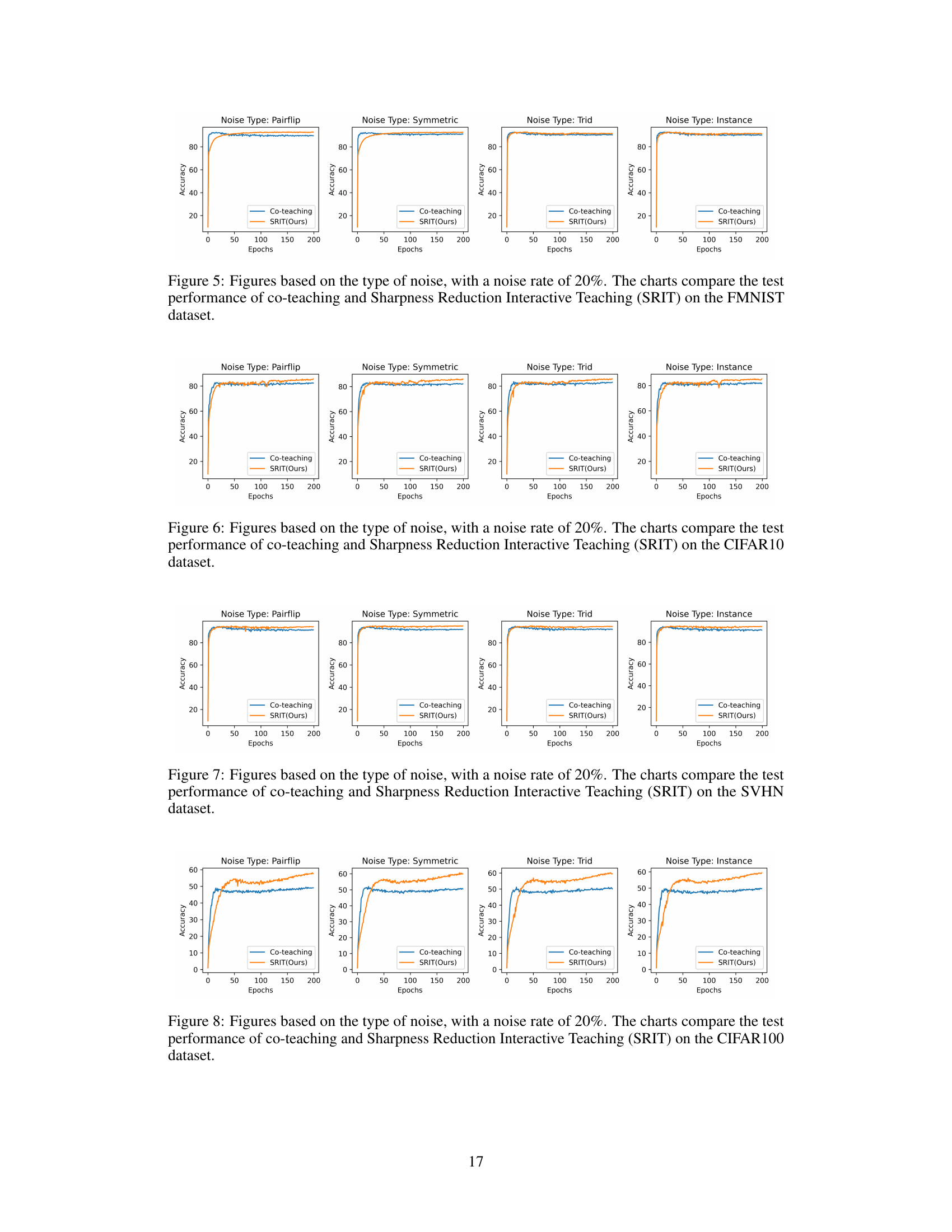
This figure displays the testing performance of five datasets (MNIST, FMNIST, CIFAR10, CIFAR100, SVHN) under four different noise types (Pairflip, Symmetric, Tridiagonal, Instance) and with a noise rate of 20%. The charts compare the performance of co-teaching and the proposed Sharpness Reduction Interactive Teaching (SRIT) method. It visually demonstrates the improvement in accuracy and generalization capability achieved by SRIT across different datasets and noise types. The x-axis represents the training epochs, and the y-axis represents the test accuracy.
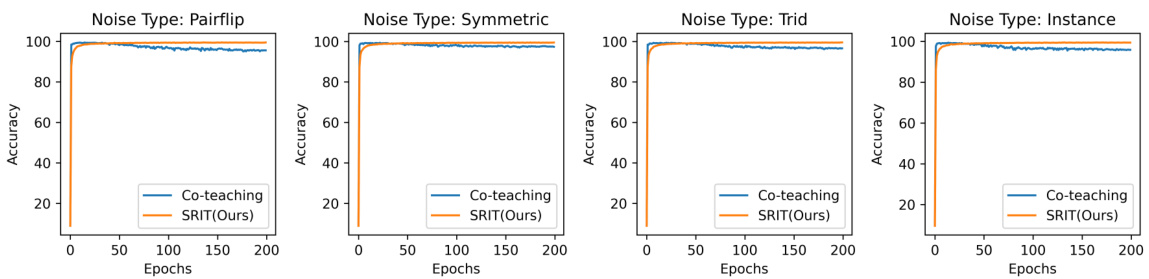
This figure shows the test accuracy of five datasets (MNIST, FMNIST, CIFAR10, SVHN, CIFAR100) under four different noise types (Pairflip, Symmetric, Tridiagonal, Instance) with a noise ratio of 20%. The results compare the performance of co-teaching and the proposed SRIT (Sharpness Reduction Interactive Teaching) method. Each subplot represents a dataset and shows how the test accuracy changes over epochs for each noise type and algorithm. The plots visually demonstrate that SRIT consistently achieves better generalization performance compared to co-teaching across all datasets and noise types.
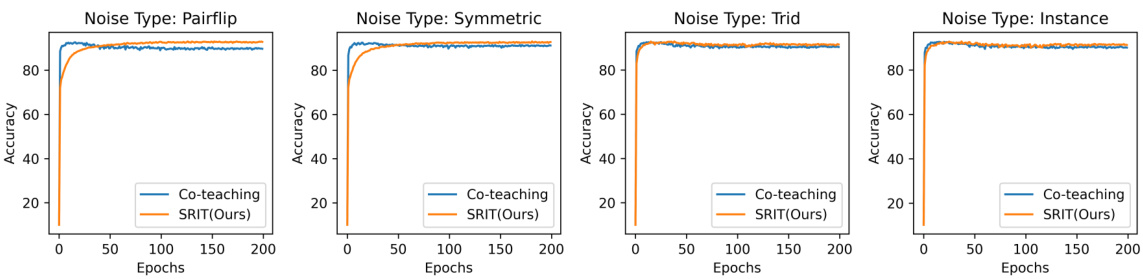
This figure displays the accuracy performance of the co-teaching and SRIT (Sharpness Reduction Interactive Teaching) methods across five different datasets (MNIST, FMNIST, CIFAR10, SVHN, CIFAR100) under four types of noise (Pairflip, Symmetric, Tridiagonal, Instance) with a noise rate of 20%. Each subplot represents a specific noise type, showing accuracy plotted against epochs for both co-teaching and SRIT. The purpose is to visually compare the performance of the two methods under various noise conditions and across diverse datasets.

This figure displays the accuracy performance of the Co-teaching and SRIT methods across five datasets (MNIST, FMNIST, CIFAR10, SVHN, and CIFAR100) under four different noise types (Pairflip, Symmetric, Tridiagonal, and Instance) with a noise ratio of 20%. Each subplot represents a dataset, and within each subplot, the accuracy curves for Co-teaching and SRIT are shown. The figure demonstrates the superior generalization performance of SRIT across various datasets and noise types.
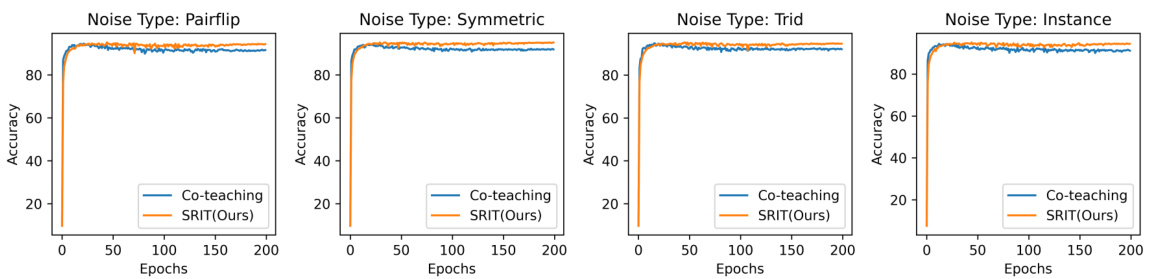
This figure shows the test accuracy for five datasets (MNIST, FMNIST, CIFAR10, SVHN, and CIFAR100) with four different noise types (Pairflip, Symmetric, Trid, and Instance) at a noise rate of 20%. Each subplot represents a different dataset and shows the accuracy over epochs for both the co-teaching and the SRIT (Sharpness Reduction Interactive Teaching) methods. The plots visually compare the performance and convergence speed of the two methods under various noise conditions.

This figure displays the test accuracy over epochs for five datasets (MNIST, FMNIST, CIFAR10, SVHN, CIFAR100) under four different noise types (Pairflip, Symmetric, Trid, Instance) with a noise rate of 20%. It compares the performance of the co-teaching method with the proposed SRIT (Sharpness Reduction Interactive Teaching) method. The plots visualize how the accuracy changes over the training epochs for each method, dataset, and noise type, showing SRIT’s generally superior performance and robustness to noisy data.
Full paper#