↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world problems involve finding the best solution among countless possibilities, a challenge known as combinatorial optimization. Current methods often struggle due to the vast search space, frequently getting stuck in suboptimal solutions. This paper tackles this issue by shifting focus from expanding the search area to actively guiding the search process.
The researchers propose a novel framework called HeO, which uses heat diffusion to transform the problem, making the optimal solution more easily accessible. HeO’s performance surpasses state-of-the-art methods across diverse problem types. This innovative method demonstrates the power of leveraging thermodynamic principles for efficient combinatorial optimization, opening exciting new pathways in algorithm design and application.
Key Takeaways#
Why does it matter?#
This paper is important because it offers a novel approach to combinatorial optimization, a pervasive problem across numerous fields. The proposed framework, leveraging heat diffusion, shows superior performance compared to existing methods. This opens up new avenues for research, particularly in integrating thermodynamic principles into AI algorithms and exploring alternative optimization strategies.
Visual Insights#
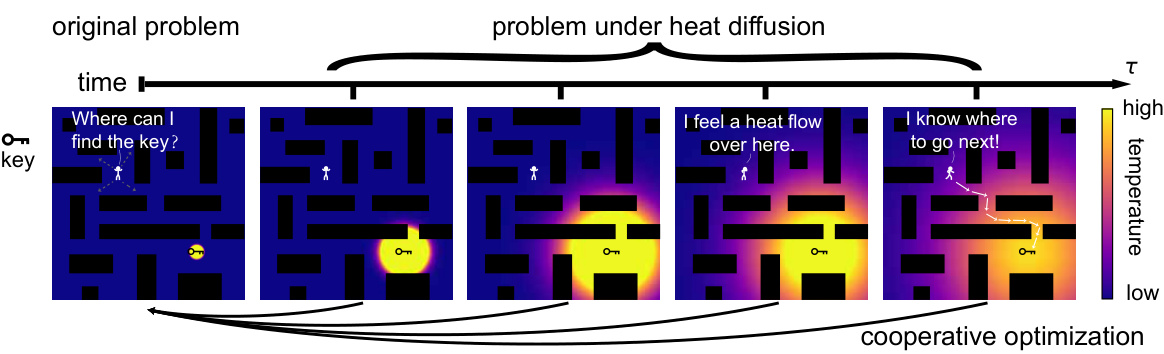
This figure illustrates the core idea of the HeO framework using an analogy. Finding a key in a dark room represents a combinatorial optimization problem. Without additional information (like light), searching is inefficient. HeO introduces heat diffusion, analogous to the key emitting heat. This heat spreads, providing gradient information from distant areas of the solution space to guide the search, improving efficiency. The figure visually represents how the heat diffuses over time, guiding the search towards the solution. The method’s cooperative optimization is highlighted.
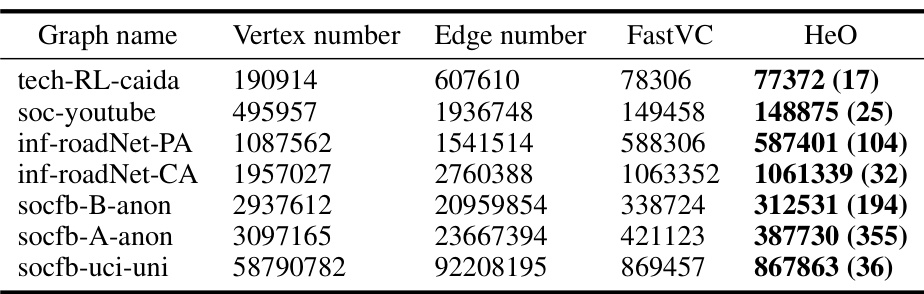
This table presents the results of minimum vertex cover experiments on seven real-world graphs using the proposed HeO algorithm and the existing FastVC algorithm. For each graph, the table lists the number of vertices, the number of edges, the size of the vertex cover found by FastVC, and the size of the vertex cover found by HeO. The numbers in parentheses after the HeO results indicate the difference between the sizes of vertex covers found by HeO and FastVC. This table allows a comparison of the performance of the two algorithms on various graphs with varying sizes and structures.
In-depth insights#
Heat Diffusion Optimization#
The proposed “Heat Diffusion Optimization” framework offers a novel approach to combinatorial optimization by leveraging the principles of heat diffusion. Instead of expanding the search space, it focuses on actively propagating information to the solver. By transforming the objective function while preserving the optima, heat diffusion enables efficient information flow from distant regions, guiding the solver towards solutions more effectively. This method addresses the limitations of traditional iterative methods that often get trapped in local optima due to restricted search scopes. The framework demonstrates superior performance across various challenging combinatorial optimization problems, highlighting the potential of harnessing thermodynamic principles in this field. The backward uniqueness of the heat equation is a key theoretical foundation of this approach, assuring that transformations do not alter the original problem’s solutions. This study represents a significant advancement in solving complex combinatorial optimization problems by efficiently utilizing gradient information and demonstrating the cooperative optimization capabilities of the methodology.
Gradient Descent Failure#
The section ‘Gradient Descent Failure’ likely explores the inherent challenges of applying gradient descent methods to combinatorial optimization problems. Combinatorial problems’ discrete nature clashes with gradient descent’s reliance on continuous, differentiable functions. The authors probably demonstrate how directly applying gradient-based approaches often leads to suboptimal solutions, getting trapped in local minima due to the complex, non-convex landscape of the solution space. The limitations of Monte Carlo gradient estimation (MCGE), a common approach to address the differentiability issue, is likely highlighted. MCGE’s high variance and susceptibility to local optima, despite transforming the problem into a differentiable form, likely underscores the fundamental incompatibility between the methods. The discussion probably sets the stage for introducing the paper’s proposed solution – leveraging heat diffusion to facilitate more effective navigation of the solution space and overcome the limitations of traditional gradient descent methods for combinatorial optimization problems.
HeO Algorithm#
The HeO algorithm, a novel framework for combinatorial optimization, leverages heat diffusion to enhance the solver’s ability to locate optimal solutions. Unlike traditional methods that focus on expanding the search scope, HeO actively propagates information from distant regions of the solution space through a heat diffusion process. This clever transformation of the target function, while preserving optimal locations, facilitates efficient navigation by guiding the solver towards optima using gradient information from various temperature distributions. The algorithm’s cooperative optimization approach, involving gradients from different heat diffusion versions, allows for superior performance across diverse challenging combinatorial problems. Backward uniqueness of the heat equation ensures the original optima remain unchanged during the diffusion process. The method demonstrates a significant advantage over existing gradient-based and other approximate methods by showcasing its efficiency and scalability in tackling various problem types, ranging from quadratic and polynomial to binary and ternary scenarios. The core strength of HeO lies in its ability to efficiently harness the thermodynamic principle of heat diffusion, enabling more effective information flow across the entire solution space and potentially offering new paths towards solving computationally intractable problems.
Experimental Results#
The “Experimental Results” section of a research paper is crucial for demonstrating the validity and effectiveness of the proposed methods. A strong presentation will include rigorous comparisons against relevant baselines using multiple challenging datasets, showcasing improvements in key metrics. Error bars or other statistical measures are essential to validate significance and avoid overstating results. The choice of evaluation metrics should be justified, and the results should be presented clearly using visualizations (such as charts and graphs), alongside a thorough discussion of any unexpected or outlying results. Detailed ablation studies can show the impact of individual components in the proposed approach. If applicable, the paper should also discuss the generalizability of the findings and their robustness across varying conditions. Ultimately, a well-crafted “Experimental Results” section builds confidence in the research contributions by demonstrating their practical value and scientific rigor.
Future Work#
Future research directions stemming from this heat diffusion optimization (HeO) framework are plentiful. Extending HeO to handle integer linear programming and routing problems is crucial, as current limitations in encoding integer variables via Bernoulli distributions hinder applicability to these significant problem classes. Integrating HeO with advanced methods like Metropolis-Hastings could significantly broaden its reach. Investigating the use of general parabolic differential equations instead of the heat equation could lead to significant performance gains. Exploring non-monotonic temperature schedules (Tt) in HeO warrants further investigation to potentially enhance performance beyond the monotonic schedules currently employed. Finally, hybridizing HeO with metaheuristic algorithms could create more robust and efficient solvers for a broader range of combinatorial optimization problems. Addressing these avenues will further solidify and expand the impact of HeO across various optimization domains.
More visual insights#
More on figures

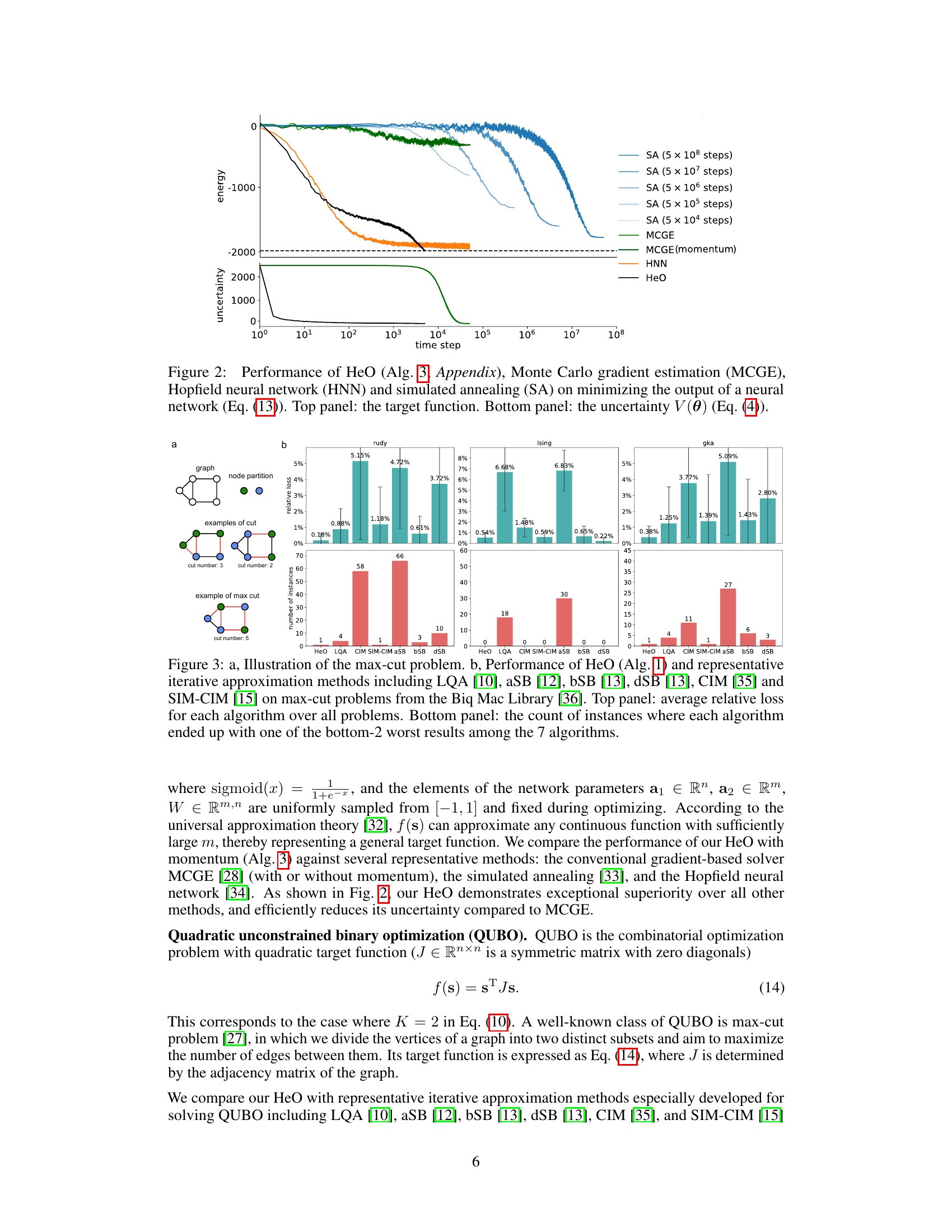
This figure compares the performance of the proposed Heat Diffusion Optimization (HeO) method against three other methods: Monte Carlo Gradient Estimation (MCGE), Hopfield Neural Network (HNN), and Simulated Annealing (SA) in minimizing a neural network’s output. The top panel shows the energy (target function) over time steps, and the bottom panel displays the uncertainty of the solution over time steps. HeO demonstrates superior performance in both minimizing the target function and reducing uncertainty.

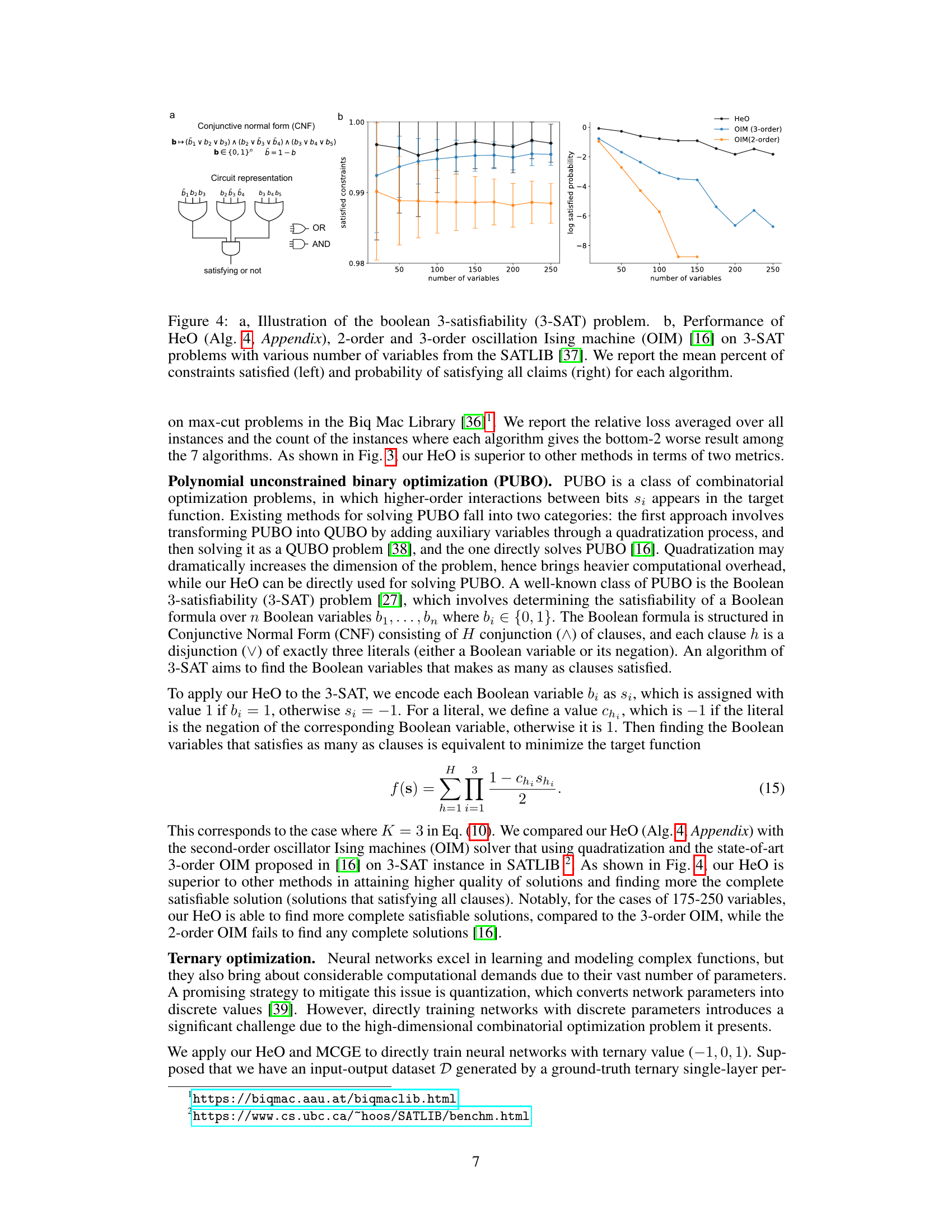
Figure 3(a) illustrates the max-cut problem, which involves partitioning the nodes of a graph into two sets to maximize the number of edges between the sets. Figure 3(b) compares the performance of the proposed Heat Diffusion Optimization (HeO) algorithm against six other iterative approximation methods (LQA, aSB, bSB, dSB, CIM, SIM-CIM) on a set of max-cut problems from the Biq Mac Library. The top panel shows the average relative loss for each algorithm across all problems, while the bottom panel displays the number of instances where each algorithm performed among the two worst.
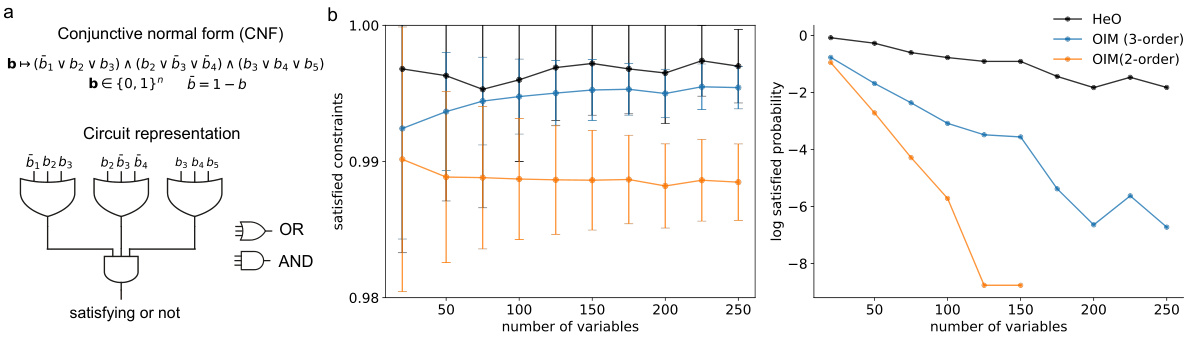
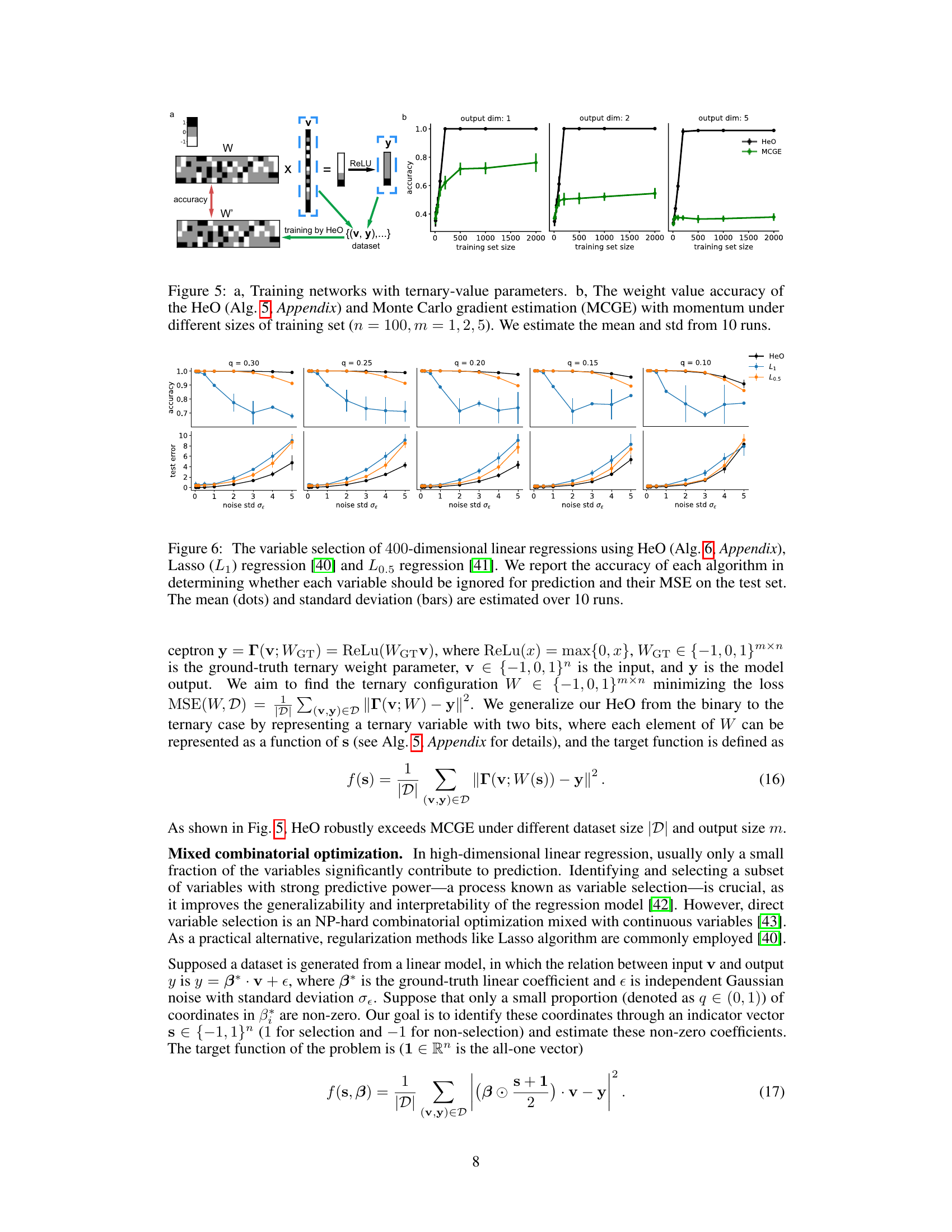
This figure illustrates the Boolean 3-satisfiability (3-SAT) problem and presents a performance comparison of different algorithms, namely HeO, 2-order OIM, and 3-order OIM, for solving 3-SAT problems with varying numbers of variables. Subfigure (a) shows a visual representation of the 3-SAT problem using a circuit diagram. Subfigure (b) shows two plots: the first showing the mean percentage of satisfied constraints, and the second displaying the log of the probability of satisfying all constraints, as a function of the number of variables. Error bars are included.
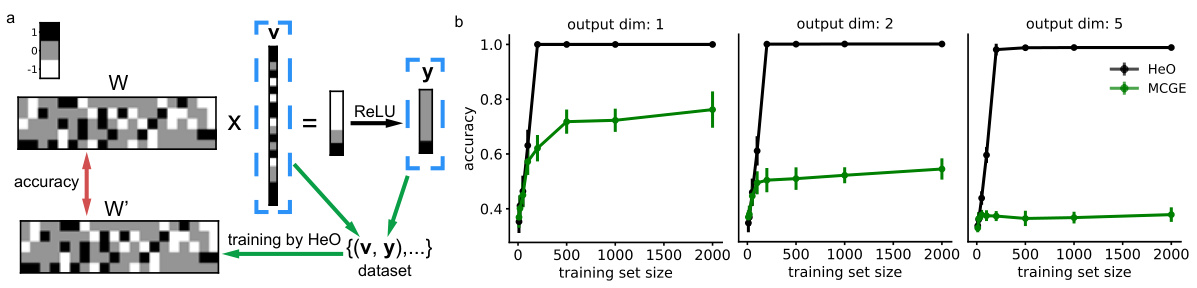
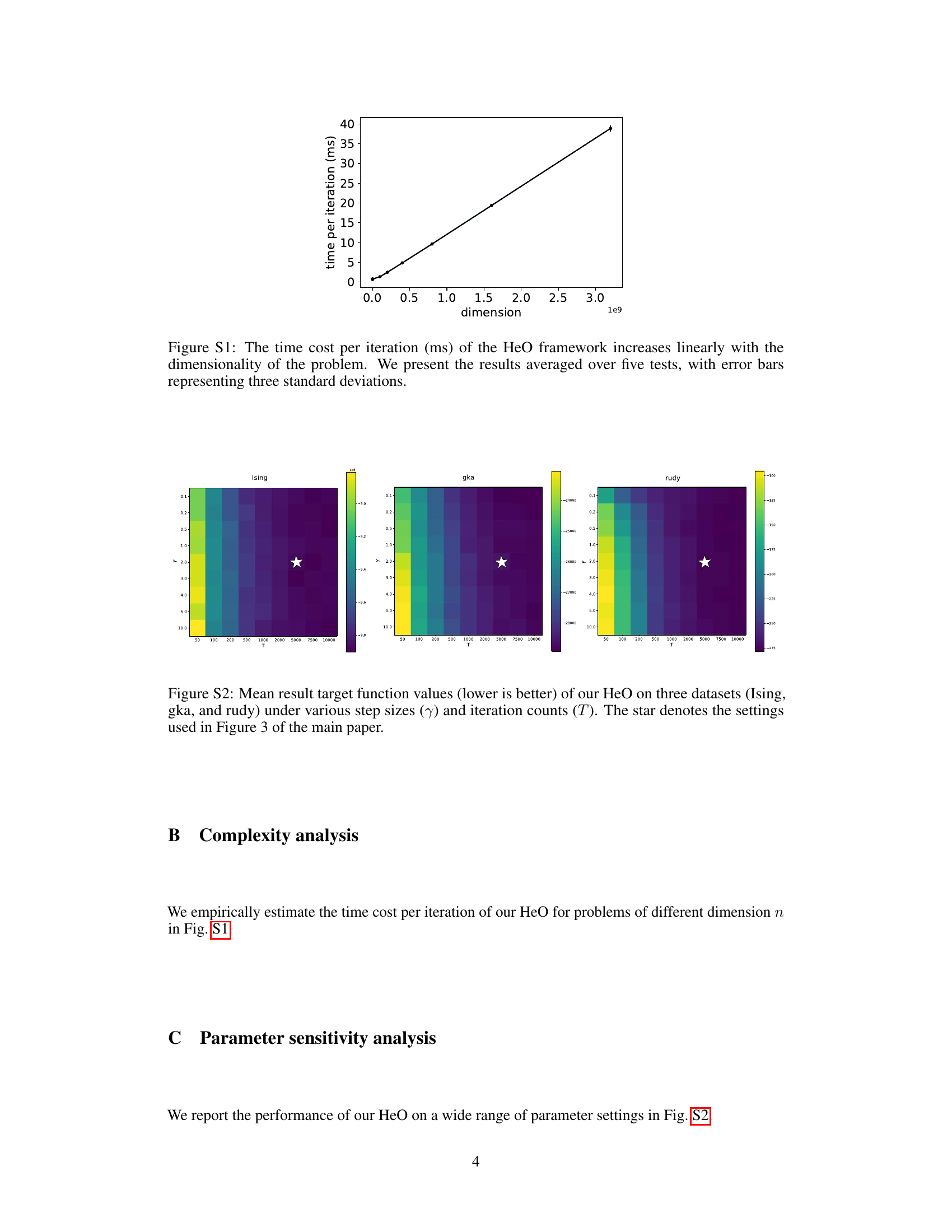
Figure 5 shows the results of training neural networks with ternary-value parameters using the proposed HeO algorithm and the conventional MCGE method. Panel (a) illustrates the training process, depicting the ternary weight matrix W, input vector v, ReLU activation, output vector y, and the resulting trained weight matrix W’. Panel (b) presents the accuracy results for different output dimensions (m = 1, 2, 5) and varying training set sizes, demonstrating the superior performance of HeO in terms of weight accuracy.
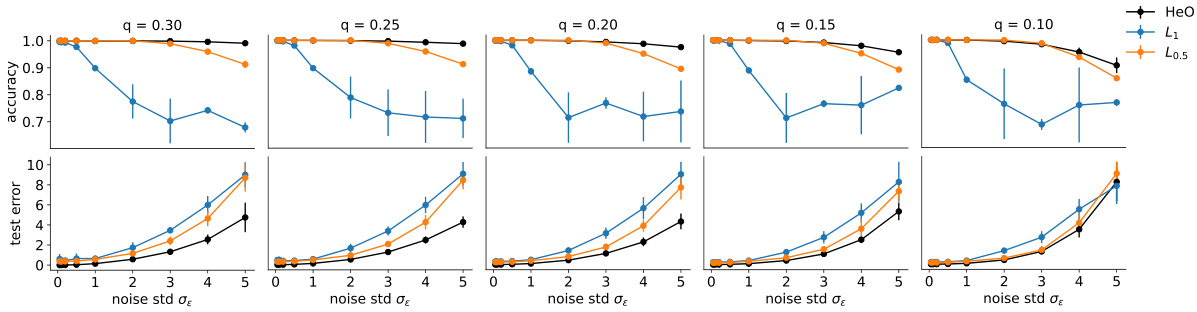
This figure compares the performance of HeO against Lasso (L1) and L0.5 regression methods for variable selection in 400-dimensional linear regression. It shows the accuracy of each method in identifying irrelevant variables (those with zero coefficients in the true model) and the mean squared error (MSE) on test data, for various sparsity levels (controlled by the parameter q) and noise levels (controlled by the parameter σe). The results, averaged across 10 runs, demonstrate HeO’s superior accuracy and lower MSE compared to the other methods.

This figure illustrates the core idea of the Heat Diffusion Optimization (HeO) framework using an analogy. Searching for a key in a dark room represents solving a combinatorial optimization problem. The traditional method (touching around) is slow and inefficient. HeO introduces heat diffusion, where the key emits heat, allowing the person to efficiently locate the key (optima). The heat diffusion transforms the target function, creating a temperature gradient which helps guide the solver to the optimum more efficiently.
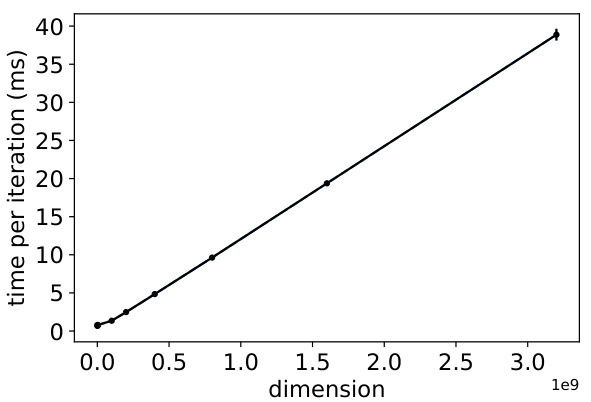
This figure shows the time cost per iteration of the Heat Diffusion Optimization (HeO) framework plotted against the dimensionality of the problem being solved. The results are averaged over five independent runs, and error bars (representing three standard deviations) illustrate the variability in the measurement. The linear relationship indicates that the computational cost of HeO scales linearly with problem size. This is important because it suggests HeO’s efficiency remains consistent even when tackling large-scale combinatorial optimization problems.
This figure compares the performance of the proposed HeO algorithm against three other optimization algorithms: Monte Carlo gradient estimation (MCGE), Hopfield neural network (HNN), and simulated annealing (SA). The task is to minimize the output of a neural network, which serves as a toy example for demonstrating the capabilities of HeO. The top panel shows the target function and the bottom panel displays the uncertainty in the output distribution, providing a measure of how efficiently each algorithm reduces uncertainty. HeO exhibits superior performance compared to the other algorithms.
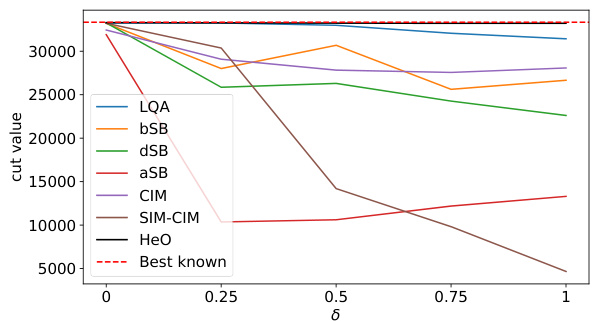
This figure shows the result of max-cut problem on K-2000 dataset when the control parameters are perturbed with different random perturbation level (δ). The x-axis represents the random perturbation level. The y-axis represents the best cut value among 10 runs. The red dash line represents the best known cut value. The figure shows that the performance of HeO is more robust to the random perturbation compared to other algorithms. This result verifies that HeO has a cooperative optimization mechanism.
More on tables

This table compares the performance of the proposed HeO algorithm (Algorithm 7 from the Appendix) and the existing FastVC algorithm [44] for solving the Minimum Vertex Cover (MVC) problem. It shows the number of vertices and edges in several real-world graphs from the benchmark datasets used in the experiments and then presents the vertex cover sizes obtained by both HeO and FastVC for each graph. The results demonstrate HeO’s effectiveness in finding smaller vertex covers compared to FastVC, especially on large graphs.

This table presents a comparison of the performance of the proposed HeO algorithm (Algorithm 7 in the Appendix) and the existing FastVC algorithm [44] on solving the Minimum Vertex Cover (MVC) problem for several real-world graphs. For each graph, the table lists the number of vertices, the number of edges, the size of the vertex cover found by FastVC, the size of the vertex cover found by HeO, and the numbers in parentheses after HeO results indicate that those results are obtained from running Algorithm 7 and not Algorithm 1, which is a different algorithm and would have different results.
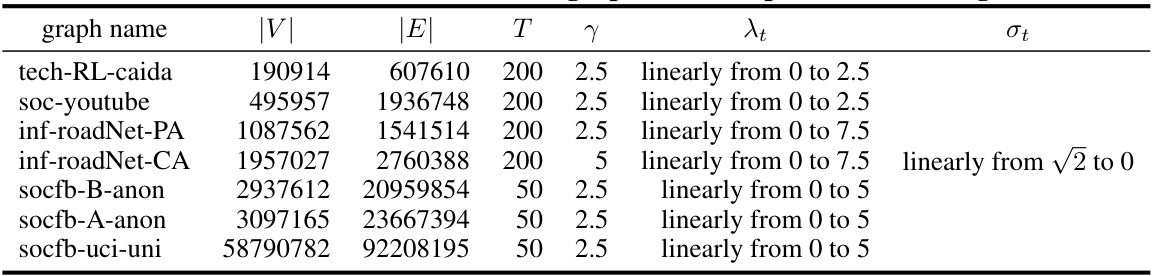
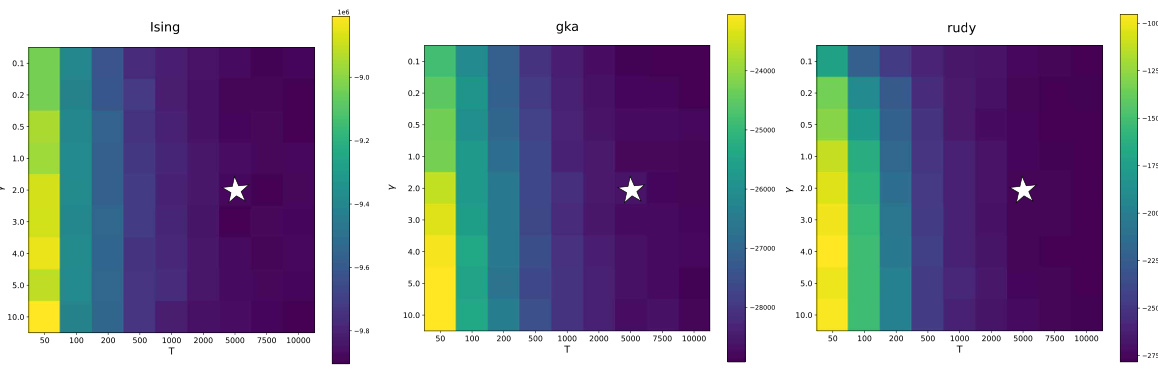
This table presents the results of the Minimum Vertex Cover (MVC) problem on several real-world graphs. It compares the performance of the proposed Heat Diffusion Optimization (HeO) algorithm (Algorithm 7 from the Appendix) against the FastVC algorithm [44]. The table shows the number of vertices (|V|), the number of edges (|E|), the number of iterations (T), the step size (γ), the schedule of σt, and the size of the vertex cover found by each algorithm. The vertex cover size for HeO is reported as the average over 10 runs.

This table presents the experimental results of the Minimum Vertex Cover (MVC) problem. It compares the performance of the proposed HeO algorithm (Algorithm 7 in the Appendix) against the FastVC algorithm [44] on several real-world graphs. The table lists the name of each graph, the number of vertices and edges in the graph, the size of the minimum vertex cover found by FastVC, the size of the minimum vertex cover found by HeO, and the number of iterations used by HeO in parentheses. This allows for a direct comparison of the two algorithms’ effectiveness in solving the MVC problem on various graph structures.
Full paper#