TL;DR#
Constrained Markov Decision Processes (CMDPs) are a critical area of research in reinforcement learning, addressing the challenge of optimizing cumulative rewards while adhering to constraints. However, existing approaches often rely on conservative worst-case bounds, leading to suboptimal performance in practice. A key challenge is the lack of optimal, problem-dependent guarantees, which are more accurate than worst-case bounds. This hinders progress towards developing more efficient algorithms.
This paper tackles these issues by developing a novel algorithm for CMDPs. The algorithm operates in the primal space by resolving a primal linear program (LP) adaptively. By characterizing instance hardness via LP basis, the algorithm efficiently identifies an optimal basis and resolves the LP adaptively. This results in a significantly improved sample complexity bound of Õ(1/ε), surpassing the state-of-the-art O(1/ε²) bound. The improved complexity is achieved by utilizing instance-dependent parameters and adaptive updates of the linear program. The paper’s contributions are a significant advancement in reinforcement learning theory and algorithm design for CMDPs.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in reinforcement learning and optimization because it presents the first instance-dependent sample complexity bound of Õ(1/ε) for constrained Markov Decision Processes (CMDPs). This significantly improves upon the existing state-of-the-art and provides a more practical and efficient approach for solving CMDP problems. The techniques developed could also inspire new algorithms and theoretical analyses in online linear programming and related fields. The result has implications on both theory and algorithm design and opens up new directions for future research.
Visual Insights#
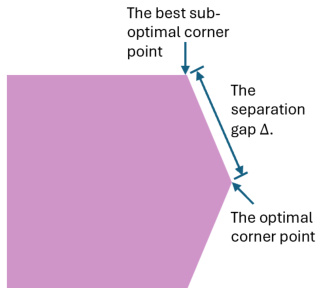
🔼 This figure illustrates how the problem instance hardness is characterized using the linear programming (LP) basis. The shaded area represents the feasible region of policies in the LP formulation. The optimal policy is a corner point of this polytope, and its distance from the nearest suboptimal corner point defines the hardness gap Δ. A larger gap indicates an easier problem instance, while a smaller gap indicates a harder problem instance.
read the caption
Figure 1: A graph illustration of the hardness characterization via LP basis, where the shaded area denotes the feasible region for the policies.
Full paper#



















