Efficient Policy Evaluation Across Multiple Different Experimental Datasets

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on policy evaluation and causal inference, particularly those dealing with heterogeneous data from multiple sources. It offers novel solutions for improving the accuracy and reliability of policy effect estimations across diverse settings, ultimately advancing the field’s practical applicability.

Visual Insights

#

This figure displays four causal diagrams (a, b, c, d) that illustrate the inference of a two-stage treatment strategy (π₀) from data in two source domains (M¹, M²). Each diagram represents a different combination of interventions, policies and domain discrepancies, highlighting how they influence the identifiability of the target policy effect in the target domain. The selection diagrams (c, d) highlight the discrepancies (i.e., missing edges) between the target and source domains. This visualization supports the identification criteria developed in the paper, which helps to determine whether the effect of a policy can be expressed using adjustment formulas obtained from different distributions generated by separate policy interventions.

In-depth insights

#

Multi-Domain Policy

#

A multi-domain policy approach in a research paper would likely explore the challenges and opportunities of designing and implementing policies that effectively address problems across diverse and interconnected domains. It would necessitate considering the unique characteristics, constraints, and priorities of each domain involved, while also seeking synergies and commonalities to develop a unified approach. A key aspect would be the development of robust and flexible mechanisms that can adapt to domain-specific variations, perhaps using data-driven approaches to inform decision-making. Furthermore, the paper might delve into the evaluation methods needed to measure the success of the multi-domain policy in each domain and across all domains involved, acknowledging the difficulties of aggregation and comparison across disparate metrics. Ethical considerations are crucial, ensuring fairness and avoiding unintended negative consequences in any particular domain due to a decision made in another. The overall aim is to create a policy that is not only effective but also equitable and sustainable across all relevant domains.

Robust Estimation

#

Robust estimation methods are crucial for reliable causal inference, especially when dealing with finite samples or model misspecifications. The paper highlights the importance of developing estimators that are multiply robust, meaning they remain consistent even if some, but not all, of the working models are incorrect. This is particularly valuable in real-world scenarios where data may be collected under diverse conditions and the true underlying data generating processes are uncertain. The proposed estimators leverage techniques like doubly robust estimation and double machine learning, extending them to handle multiple datasets collected under differing interventions and settings. The asymptotic analysis provides convergence guarantees, offering theoretical support for the estimators’ reliability. The empirical evaluations using synthetic and real-world data demonstrate the improved accuracy and robustness compared to alternative methods, underscoring the practical value of the proposed approach for reliable policy evaluation.

DML for OPE

#

Double Machine Learning (DML) offers a powerful approach for off-policy evaluation (OPE) by mitigating bias stemming from the mismatch between the behavior and target policies. DML’s key strength lies in its robustness against misspecification of nuisance functions, such as the propensity score or regression functions. This robustness is achieved through a double-debiasing technique where multiple machine learning models are trained and used to estimate the target policy’s effect. One advantage is its ability to handle complex, high-dimensional data, often encountered in real-world OPE scenarios, where simpler methods might fail. However, the performance of DML relies heavily on the quality of the machine learning models, and careful model selection and tuning are crucial. Although DML generally provides accurate OPE estimates, it’s computationally more intensive compared to other methods. The asymptotic properties of DML estimators provide theoretical guarantees, ensuring the consistency and efficiency of the estimates as the sample size increases, though these guarantees may not hold in the finite sample regime. Ultimately, DML presents a valuable tool in the OPE toolbox, especially when robustness and high dimensionality are key concerns, but careful implementation is essential to fully realize its potential.

Asymptotic Analysis

#

An asymptotic analysis in a research paper typically focuses on the behavior of estimators or algorithms as the sample size or other relevant parameters approach infinity. It provides crucial theoretical guarantees about the performance of methods under ideal conditions. Convergence rates, indicating how quickly estimators approach true values, are often derived. The analysis might also reveal the asymptotic distribution of estimators, useful for constructing confidence intervals or conducting hypothesis tests. This analysis is important because it establishes the consistency of the proposed methods (do they get closer to the truth as data increases) and their efficiency. However, it is crucial to note that asymptotic analysis might not always reflect finite-sample performance; real-world datasets are finite, and asymptotic properties don’t always translate directly to practical scenarios. Therefore, simulation studies are typically conducted to assess performance under realistic conditions. The presence of asymptotic analysis in a paper enhances the credibility and theoretical rigor of the work, particularly when combined with a thorough evaluation of finite-sample performance.

External Validity

#

The concept of external validity in the provided research paper centers on the generalizability of causal inferences derived from experimental data. The authors highlight the common issue where experimental findings may not translate seamlessly to real-world settings (target domains) due to differences in data distributions between source and target environments. This discrepancy stems from variations in population characteristics, contexts, or even the policies under evaluation. Addressing this challenge requires careful consideration of domain discrepancies and the mechanisms that govern causal relationships. The paper proposes novel methods to improve the accuracy of policy evaluations by integrating data from multiple experimental studies, emphasizing the importance of accounting for differences in distributions when aiming for reliable and generalizable conclusions. Multiply robust estimators and graphical criteria are introduced to enhance the robustness and accuracy of these estimations, ensuring results are less susceptible to model misspecification and bias. This work contributes significantly to improving the practical applicability of causal inferences beyond the specific constraints of the experimental setup, thereby promoting real-world relevance and decision-making efficacy.

More visual insights

#

More on figures

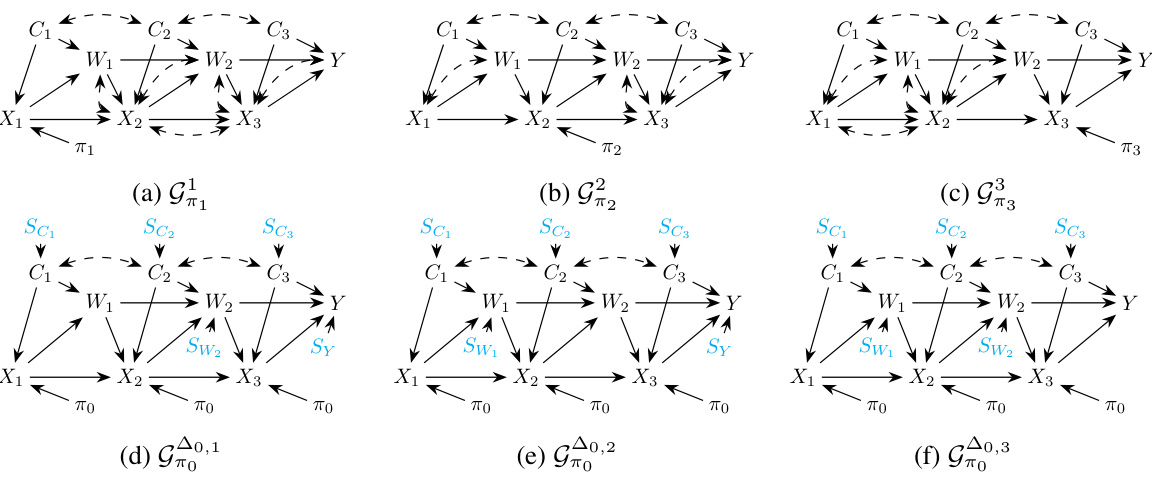
This figure shows four graphs (a) to (d) illustrating the inference of a two-stage treatment strategy. Each graph represents a different causal relationship between variables (C₁, C₂, X₁, X₂, W, Y) and a hypothetical policy (π₀). The graphs depict the causal relationships (with arrows indicating the direction of influence) and discrepancies between domains. The letters in the graphs indicate the variables: C represents covariates, X represents actions or treatments, W represents intermediate outcomes, Y represents the final outcome. Graphs (a) and (b) show the source domains (M¹ and M²), while graph (c) shows the target domain (M⁰), and (d) shows the combined data structure for inference. The selection diagrams, denoted with the Δ symbol, show the assumed discrepancies in mechanisms across domains.

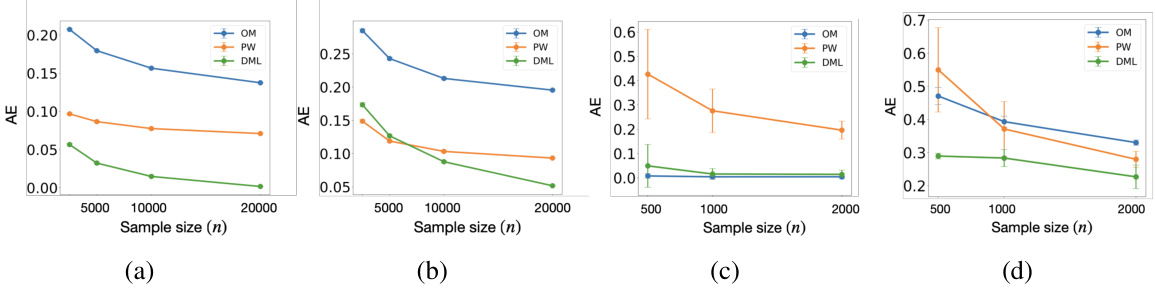
The figure compares the performance of three different policy estimators (OM, PW, and DML) on both synthetic and real-world datasets. Panels (a) and (b) show results from synthetic data, illustrating how the DML estimator converges faster and is more robust to noise than OM and PW, especially when combining data from multiple experiments. Panels (c) and (d) show similar comparisons but using real-world datasets (ACTG 175 and Project STAR), demonstrating that the DML estimator tends to converge faster and have lower absolute error.

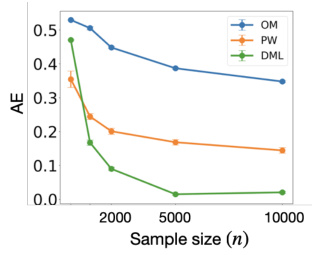
This figure compares the performance of three different policy evaluation estimators: Outcome-based model (OM), Probability-weighting-based model (PW), and Doubly Robust Machine Learning (DML) estimator. Subfigures (a) and (b) show results from synthetic data experiments with two and multiple datasets, demonstrating the DML’s superior convergence in both scenarios. Subfigures (c) and (d) present results from real-world datasets (ACTG 175 and Project STAR), illustrating DML’s faster convergence, particularly under noisy conditions, though it does not consistently outperform the other estimators in all cases.

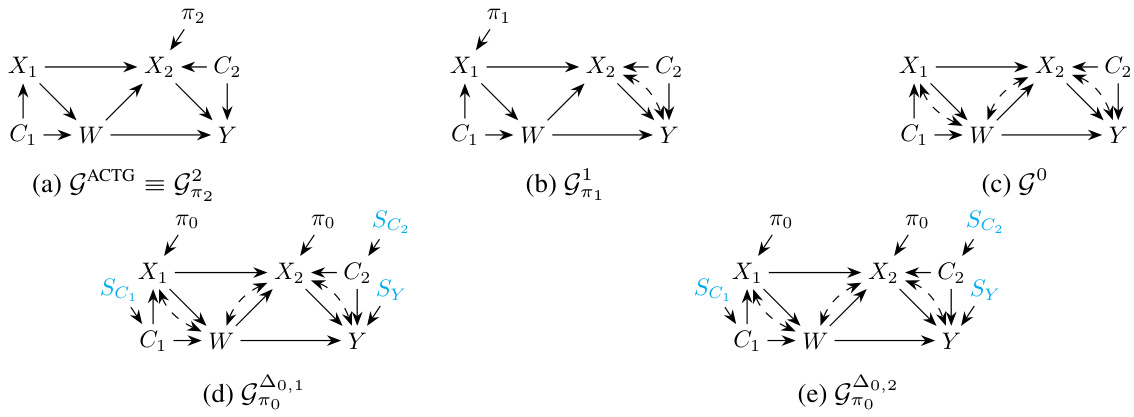
The figure displays causal diagrams and selection diagrams for the ACTG 175 experiment. It illustrates the causal relationships between variables (C1, W, X1, X2, Y) under different policies (π1, π2, π0) and highlights the discrepancies between the source and target domains through the addition of selection nodes (SC1, SC2, Sy). This visualization aids in understanding the identification and estimation challenges in policy evaluation across multiple datasets.

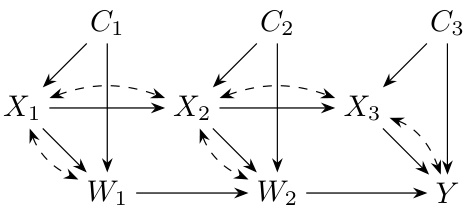
This figure shows a causal diagram for the target domain in the Project STAR study. It illustrates the relationships between variables: C (gender and ethnicity), X1, X2, X3 (student-teacher ratios in grades 0, 1, and 2 respectively), W1, W2 (intermediate academic outcomes), and Y (final academic outcome in grade 3). The dashed bidirectional arrows represent unobserved confounding. The diagram is simplified by using a single C variable to represent gender and ethnicity across all grades.

Full paper

#