↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Predicting Density Functional Theory (DFT) Hamiltonians is computationally expensive, especially for large systems, hindering progress in materials science. Traditional machine learning approaches often struggle to capture the inherent self-consistency of Hamiltonians, a critical aspect of DFT calculations. This limitation is addressed by the DEQH model, a neural network that directly addresses this self-consistency challenge.
The DEQH model cleverly integrates Deep Equilibrium Models (DEQs) into its architecture. DEQs excel at finding equilibrium states, perfectly mirroring how Hamiltonians are solved in DFT through iterative processes. By leveraging this, DEQHNet, an instantiation of the DEQH model, avoids the need for computationally intensive DFT iterations during training, enabling faster and more accurate predictions. Benchmark results on established datasets highlight DEQHNet’s superior performance, opening new avenues for more efficient and accurate DFT simulations.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel and efficient method for predicting Density Functional Theory (DFT) Hamiltonians, a crucial step in various materials science simulations. The DEQH model significantly improves prediction accuracy by directly incorporating the self-consistency inherent in DFT calculations, thus overcoming a major computational bottleneck. This work opens new avenues for research in materials discovery and design, paving the way for faster and more accurate simulations of complex systems.
Visual Insights#
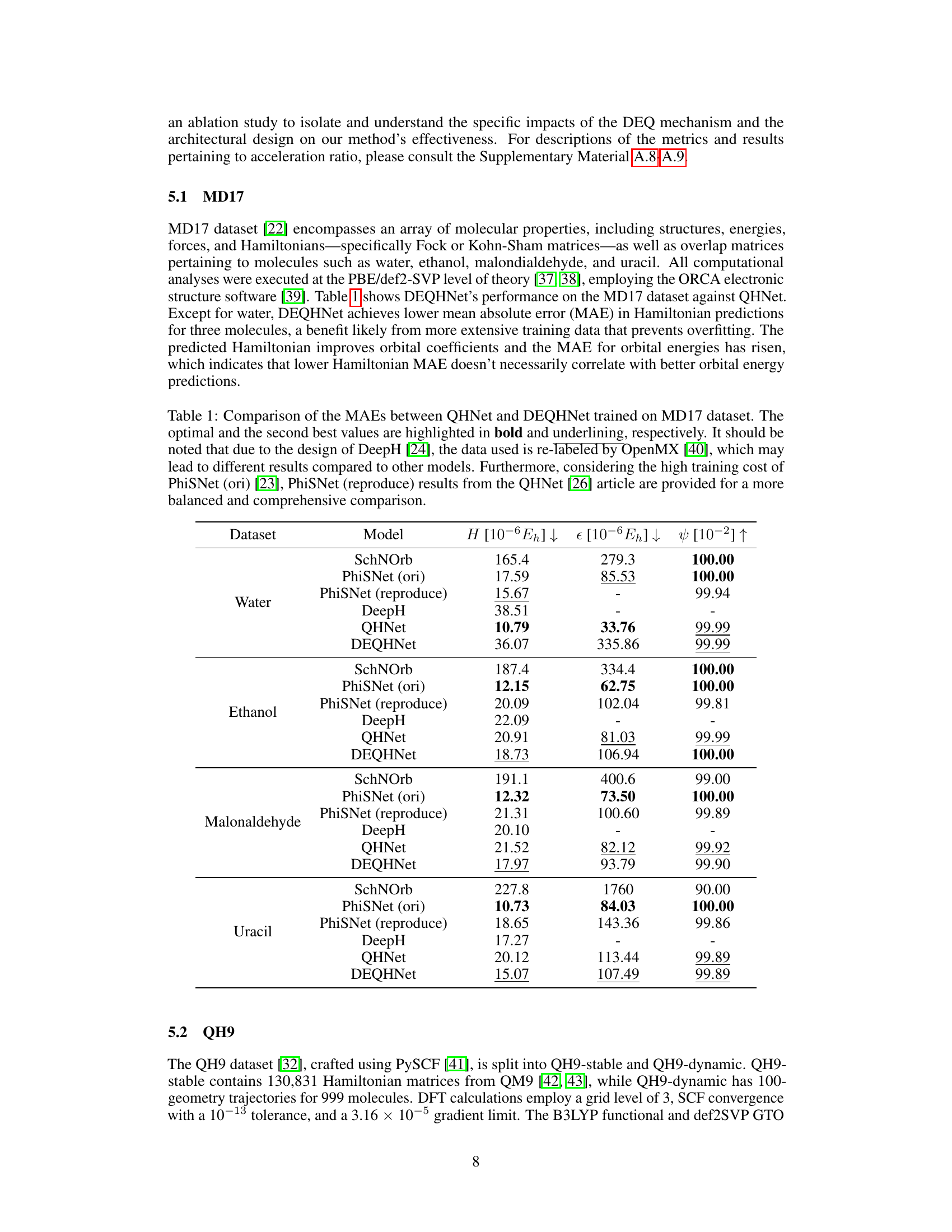
This figure shows a schematic of the Deep Equilibrium Density Functional Theory Hamiltonian (DEQH) model. The model takes as input the structural information of a molecule, the current Hamiltonian (Ht), and the overlap matrix (S). These inputs are processed by the Hamiltonian solver, which consists of two parts: the injection module (which handles structural information) and the filter module (which processes Hamiltonian and overlap matrix information). The output of the Hamiltonian solver is the next iteration of the Hamiltonian (Ht+1), which is then fed back into the model until convergence is achieved. This iterative process is key to capturing the self-consistency of the Hamiltonian in DFT.
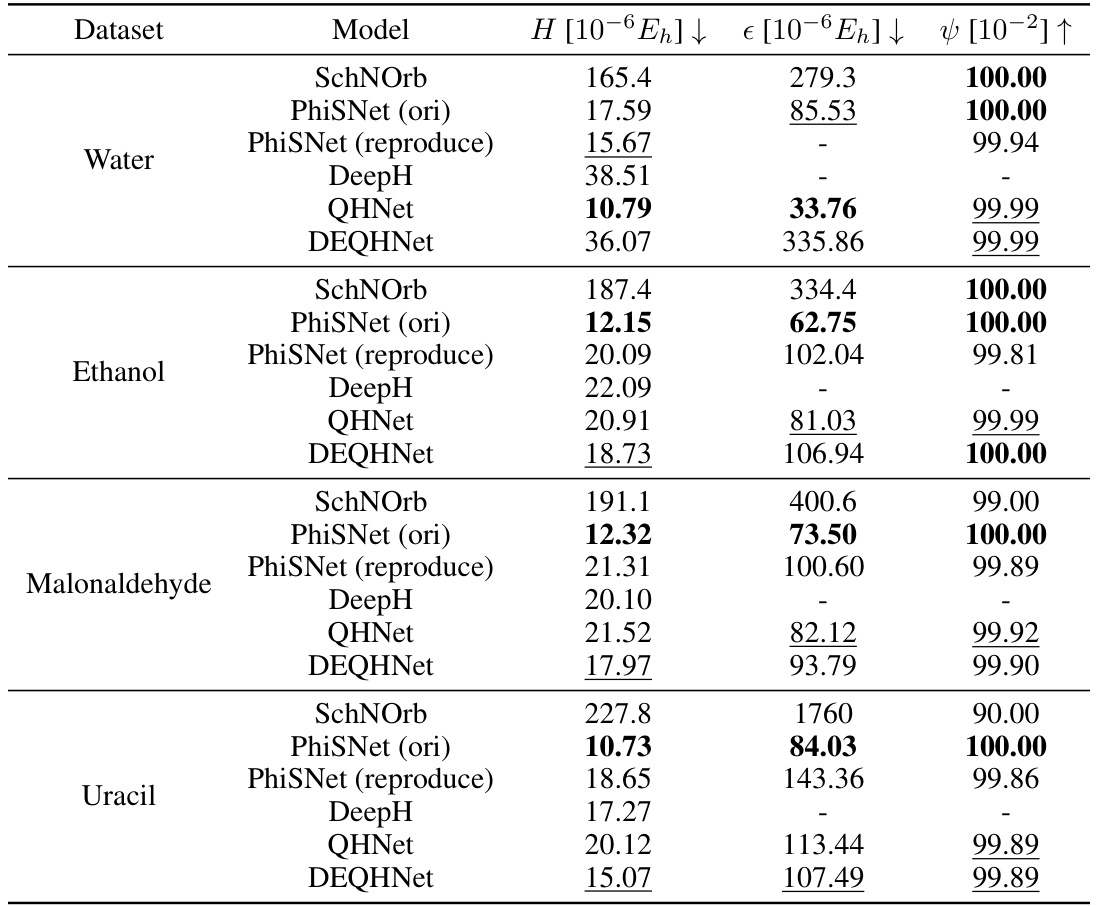
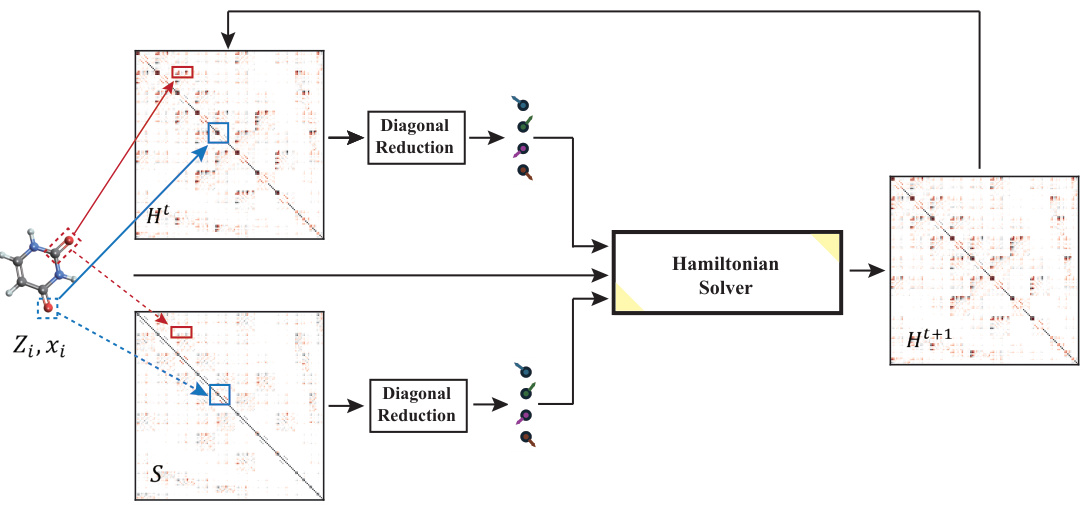
This table compares the Mean Absolute Errors (MAEs) of Hamiltonian predictions between QHNet and DEQHNet on the MD17 dataset. It highlights the best and second-best performing models for each molecule in the dataset (water, ethanol, malonaldehyde, and uracil). The table notes that differences in data preprocessing between models (specifically, DeepH’s use of OpenMX relabeled data) and the high computational cost of training PhiSNet make direct comparisons challenging. To address this, the table includes results from a reproduction of PhiSNet from the QHNet paper for more balanced comparison.
In-depth insights#
DEQ for DFT#
The application of Deep Equilibrium Models (DEQs) to Density Functional Theory (DFT) calculations represents a significant advancement in computational materials science. DFT’s self-consistent nature, involving iterative calculations to achieve convergence, makes it computationally expensive for large systems. DEQs, by their ability to efficiently find fixed-point solutions, offer a powerful alternative to traditional iterative schemes. By incorporating DEQs into the DFT framework, the new approach, which can be termed as ‘DEQ for DFT’, aims to bypass the iterative process, leading to faster and more scalable Hamiltonian predictions. This innovative approach effectively turns the Hamiltonian prediction from a time-consuming iterative task into a more direct, efficient process. The accuracy of predictions, therefore, is highly dependent on the efficiency of the DEQ solvers. The approach’s success lies in its ability to accurately capture the system’s equilibrium state. The key challenges would involve selecting suitable network architectures and loss functions to ensure both accurate and efficient convergence. Further research should focus on extending this approach to larger and more complex systems, exploring its limitations, and comparing its performance against state-of-the-art methods.
Hamiltonian Solver#
The concept of a ‘Hamiltonian Solver’ within the context of this research paper signifies a significant departure from traditional machine learning approaches to Density Functional Theory (DFT) Hamiltonian prediction. Instead of merely predicting the Hamiltonian as a fixed property, the solver iteratively refines its estimate, leveraging the inherent self-consistency of the Hamiltonian in DFT calculations. This iterative process is implemented using Deep Equilibrium Models (DEQs), which are particularly well-suited for finding fixed-point solutions, mirroring the iterative nature of the Hamiltonian’s physical definition. The implementation details, like the integration of structural information and the use of off-the-shelf neural network models within the DEQ framework, are crucial to the solver’s effectiveness. The paper highlights the solver’s ability to achieve convergence towards a self-consistent Hamiltonian without requiring explicit DFT calculations during the training phase, representing a considerable computational advantage, especially for large or complex systems. A key aspect is its versatility, making it compatible with various existing machine learning architectures. The ablation study further supports the efficacy of the approach, demonstrating the enhanced accuracy and efficiency gained by incorporating the self-consistency via DEQs.
QHNet Enhancement#
This research enhances QHNet, a deep learning model for predicting Density Functional Theory (DFT) Hamiltonians. The core improvement lies in integrating Deep Equilibrium Models (DEQs) to inherently capture the self-consistency crucial to DFT Hamiltonians, a feature often missing in traditional ML approaches. DEQs enable iterative refinement directly within the model architecture, bypassing the need for repeated DFT calculations during training, significantly improving computational efficiency and scalability. This self-consistency is key, as it allows the model to solve for the Hamiltonian iteratively, rather than just predict it directly. Benchmark results on standard datasets (MD17 and QH9) demonstrate significant improvements in prediction accuracy and suggest the DEQ integration is highly effective in capturing the inherent self-consistent iterative nature of the Hamiltonian. The integration of overlap matrices further enhances accuracy, by providing the model with additional information related to the Hamiltonian’s structure. Overall, the work introduces a novel and efficient framework for Hamiltonian prediction, suitable for larger and more complex systems than previous methods, impacting materials science.
Convergence Analysis#
A thorough convergence analysis of a deep equilibrium model (DEM) for Hamiltonian prediction would investigate several key aspects. Firstly, it should examine the rate of convergence to the equilibrium Hamiltonian, analyzing factors that influence this rate such as network architecture, hyperparameter settings, and the nature of the input data (molecular size and complexity). Secondly, the analysis should consider the stability of the convergence process; does the model always converge to a solution, or are there instances of divergence or oscillations? This would involve characterizing the behavior of the iterative solver under different conditions. The analysis should also compare the accuracy of the Hamiltonian obtained at convergence to that obtained by traditional methods and quantify improvements achieved. Finally, it is essential to address the computational cost of convergence; is the speed improvement from avoiding explicit DFT iterations significant enough to offset the iterative DEM solving process, particularly for large or complex systems? A comprehensive analysis would present these findings with sufficient statistical rigor, including error bars and multiple runs, and would discuss any observed trade-offs between speed, accuracy, and stability.
Ablation Studies#
Ablation studies systematically assess the contribution of individual components within a machine learning model. In this context, the authors likely conducted experiments removing or modifying parts of their Deep Equilibrium Hamiltonian prediction model (DEQHNet) to isolate the impact of specific architectural choices or design features. Key aspects investigated might include the role of the overlap matrix, the effectiveness of the chosen neural network architecture (e.g., QHNet), and the contribution of DEQ mechanism itself. By comparing the model’s performance with and without these elements, the ablation study aimed to demonstrate the importance of each component, providing insights into the model’s design choices and highlighting which elements are crucial for accurate Hamiltonian prediction. The results likely helped justify the final design of DEQHNet by showcasing the benefits of incorporating DEQs and the overlap matrix for self-consistency and improved prediction accuracy. The ablation analysis is vital for understanding model behavior and establishing the reliability and validity of the presented results, strengthening the overall contributions of the paper.
More visual insights#
More on figures
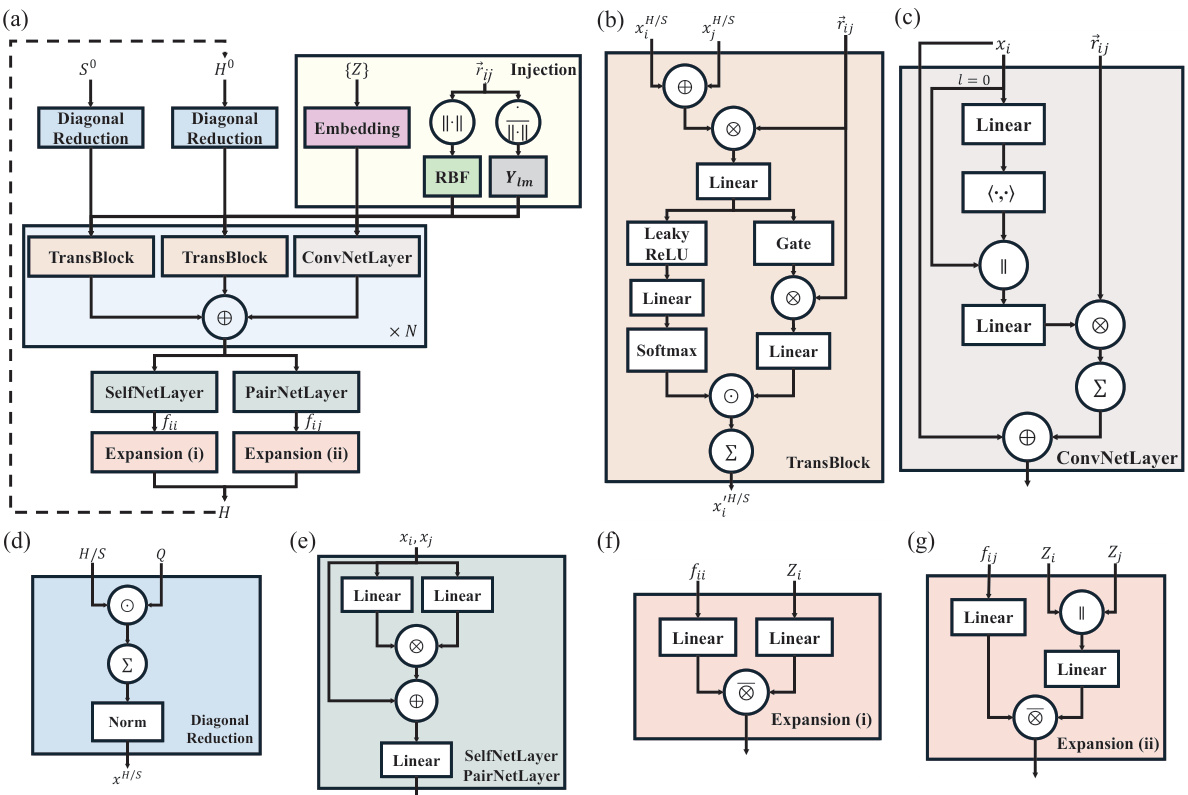
This figure shows a detailed breakdown of the DEQHNet architecture, illustrating its key components: injection, which processes structural information; filter, which processes Hamiltonian and overlap matrix data; and the DEQ solver, which iteratively refines the Hamiltonian prediction. The figure highlights the modules and pathways involved in each step of the process, from initial structural and Hamiltonian input to the final self-consistent Hamiltonian output.
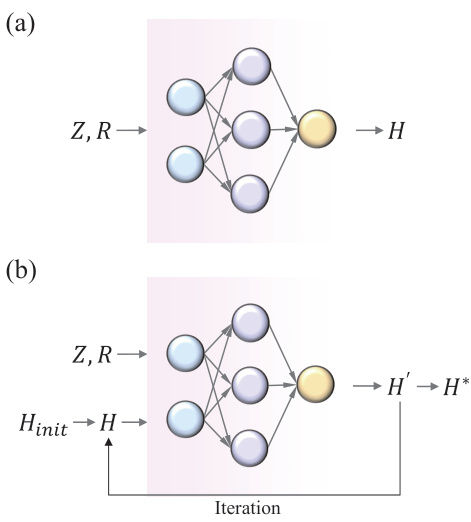
This figure illustrates the architecture of the Deep Equilibrium Density Functional Theory Hamiltonian (DEQH) model. The DEQH model is composed of two main parts: a Hamiltonian solver and an injection mechanism. The Hamiltonian solver takes the Hamiltonian, overlap matrix, and structural data as input and iteratively refines the Hamiltonian until convergence. The injection mechanism incorporates the structural information into the Hamiltonian solver. The figure highlights the iterative nature of the DEQH model, which is essential for capturing the self-consistent nature of the Hamiltonian.

This figure demonstrates the convergence behavior of the DEQHNet model. Subfigure (a) shows how the number of DEQ iterations required for convergence decreases as the model is trained for more steps. Subfigure (b) compares the convergence speed of DEQHNet to PySCF, showing that DEQHNet requires significantly fewer iterations to reach a comparable level of accuracy in Hamiltonian prediction.
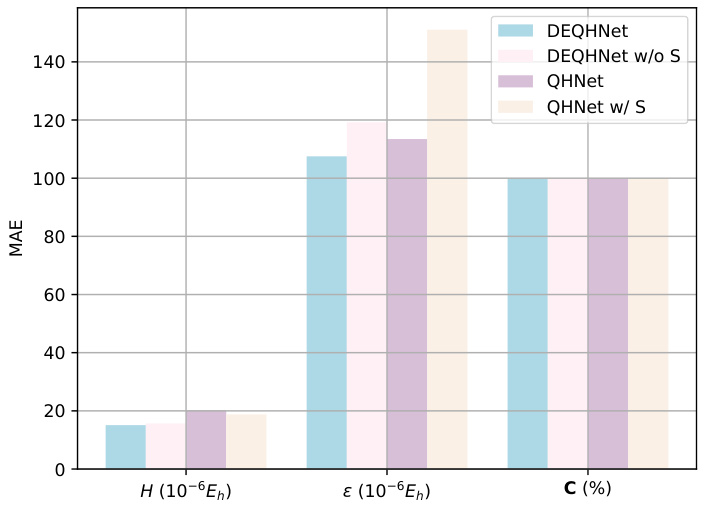
This figure presents the results of an ablation study comparing the performance of four different models on three metrics: MAE of the Hamiltonian (H), MAE of orbital energy (ε), and cosine similarity of orbital coefficients (C). The four models are: DEQHNet (the full model), DEQHNet without the overlap matrix, QHNet (baseline model), and QHNet with the overlap matrix. The results show that DEQHNet performs best overall, indicating the importance of the overlap matrix in improving the model’s performance.
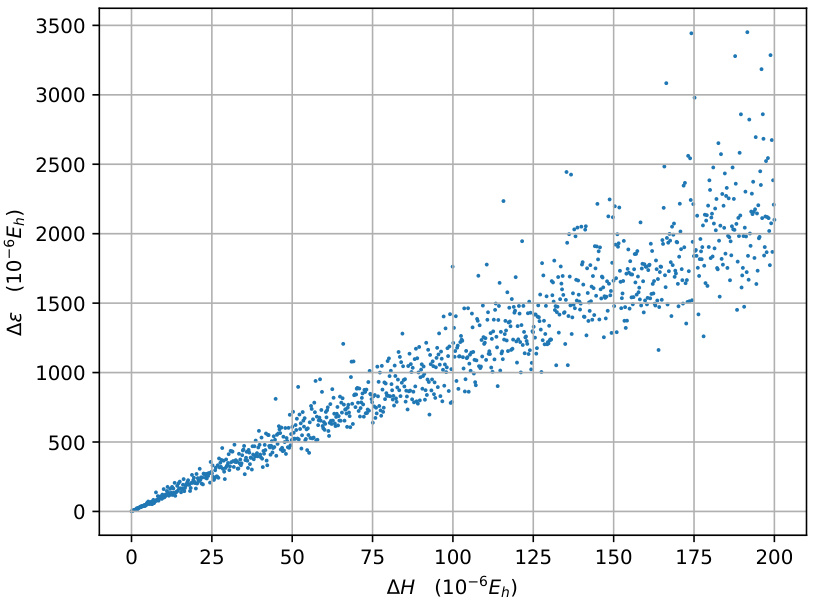
This figure shows the relationship between the error in Hamiltonian (ΔH) and the error in orbital energy (Δε). As Hermitian Gaussian noise is added to the Hamiltonian, the error in the orbital energy increases. The figure demonstrates that a smaller error in the Hamiltonian prediction leads to a smaller error in the predicted orbital energies. The relationship appears to be roughly linear, indicating a strong correlation between the accuracy of the Hamiltonian prediction and the accuracy of the orbital energy prediction.
More on tables
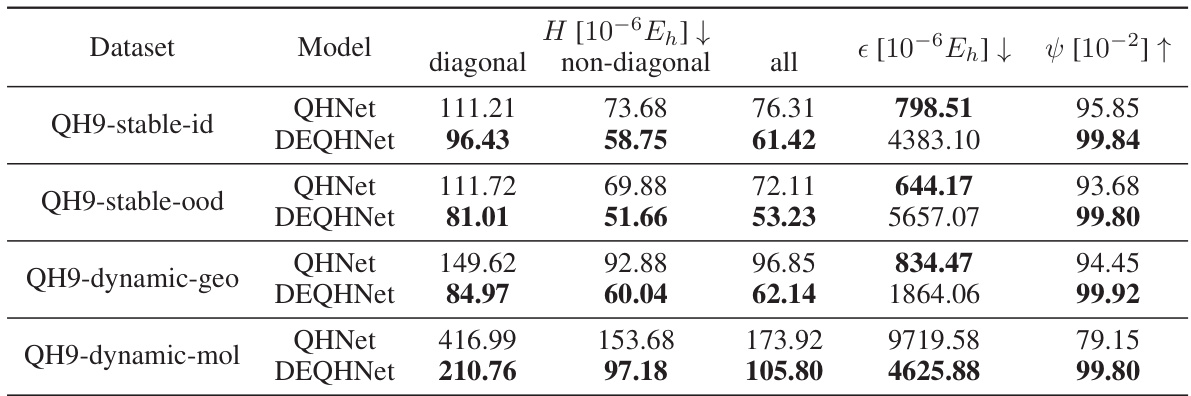
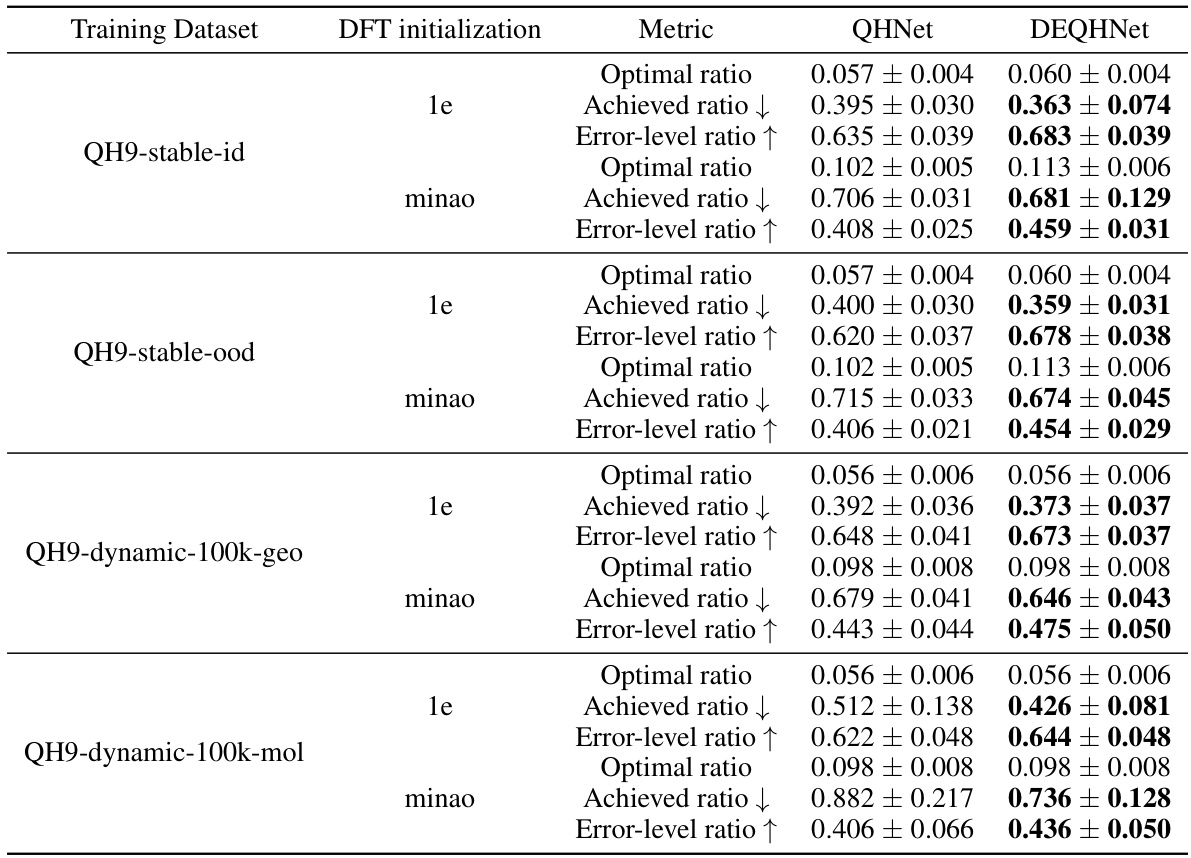
This table compares the Mean Absolute Errors (MAEs) of Hamiltonian predictions between QHNet and DEQHNet models trained on the QH9 dataset. The dataset is divided into four subsets: stable with diagonal elements only, stable with off-diagonal elements, dynamic-geometric and dynamic-molecular. The MAEs are shown for the diagonal, non-diagonal, and all elements of the Hamiltonian matrix, along with the MAE of orbital energies (∈) and the cosine similarity of orbital coefficients (ψ). The results highlight that DEQHNet significantly improves the accuracy of Hamiltonian predictions compared to QHNet across all subsets.
This table compares the Mean Absolute Errors (MAEs) of Hamiltonian predictions between QHNet and DEQHNet on the MD17 dataset. It highlights the best and second-best performing models for each molecule in the dataset and notes differences in data preprocessing and training costs that may affect comparability with other models from the literature.

This table compares the mean absolute errors (MAEs) of Hamiltonian predictions between QHNet and DEQHNet on the MD17 dataset. It highlights the best performing models for different molecules (water, ethanol, malondialdehyde, uracil) and notes that differences in data preprocessing and training cost make direct comparison challenging. The table also emphasizes that lower MAE in Hamiltonian prediction does not directly correlate with improved orbital energy prediction.
Full paper#