↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Density estimation is a critical problem across many fields, aiming to approximate a query distribution using samples from a set of known distributions. Existing methods struggle with a critical trade-off: reducing sample requirements often drastically increases the time to answer a query. This is especially challenging when dealing with numerous distributions. Prior work achieved minor improvements but left open the question of fundamental limitations.
This paper directly addresses this open question. It establishes a novel lower bound proving inherent trade-offs between sample and query complexities for density estimation, even for simple uniform distributions. This means there’s a limit to how much faster we can make such algorithms. Importantly, the authors present a new data structure with asymptotically matching upper bounds, demonstrating the tightness of their lower bound. Experimental results confirm the efficiency and practicality of their approach.
Key Takeaways#
Why does it matter?#
This paper is crucial because it establishes the first-ever limits on the best possible tradeoff between query time and sampling complexity for density estimation. It reveals fundamental statistical-computational trade-offs, impacting future algorithm design and potentially influencing various applications reliant on density estimation. The findings encourage further exploration of this trade-off across other data structure problems, leading to more efficient algorithms and a deeper understanding of these limitations. The simple data structure and experimental verification demonstrate practical relevance.
Visual Insights#
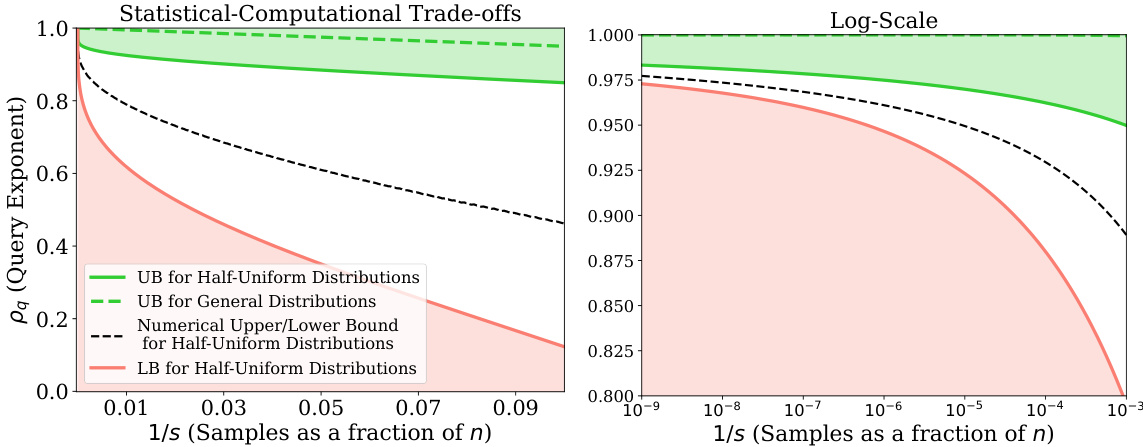
The figure shows the trade-off between the number of samples (as a fraction of n) and the query time exponent (pq) for different algorithms and bounds. The left panel displays the overall behavior, while the right panel zooms in on the region of small sample sizes. It compares an algorithm for half-uniform distributions proposed by the authors, an existing algorithm for general distributions, the authors’ analytical lower bound, and a numerical evaluation of a tighter lower bound. The figure demonstrates that the query time exponent approaches 1 as the number of samples approaches n, and that the improvement over linear time in k (number of distributions) is limited.

This table summarizes the existing results and the results obtained in the current work for the density estimation problem. It compares different algorithms in terms of the number of samples required, the query time, space complexity, and any additional comments on the approach. The table shows the tradeoffs between these parameters and highlights the improvement achieved by the current work.
Full paper#