↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Estimating mutual information (MI) accurately is essential for numerous applications, but faces challenges in high-dimensional data due to limitations in existing methods. Current neural approaches often suffer from high bias or variance. This necessitates the development of robust and efficient MI estimators for high-dimensional data.
This paper introduces f-DIME, a novel family of discriminative MI estimators based on the variational representation of f-divergence. It addresses the issues of high bias and variance by employing a novel derangement training strategy. The results demonstrate that f-DIME achieves higher accuracy and lower complexity than state-of-the-art estimators across various scenarios. The key innovation is using data derangements instead of random permutations, significantly improving estimation accuracy and resolving the limitations imposed by the upper bound of log(N).
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on mutual information estimation, particularly those dealing with high-dimensional data. It offers a novel, highly accurate, and computationally efficient method that surpasses existing approaches, improving the accuracy and scalability of various applications relying on mutual information. This work also opens up new avenues for research into discriminative MI estimation methods, variance analysis, and the role of data derangements in the training process.
Visual Insights#
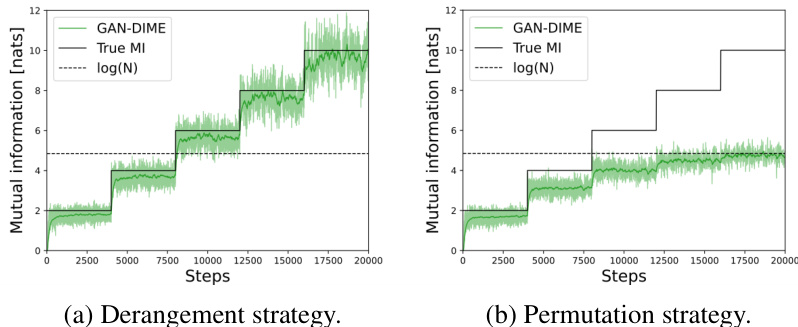
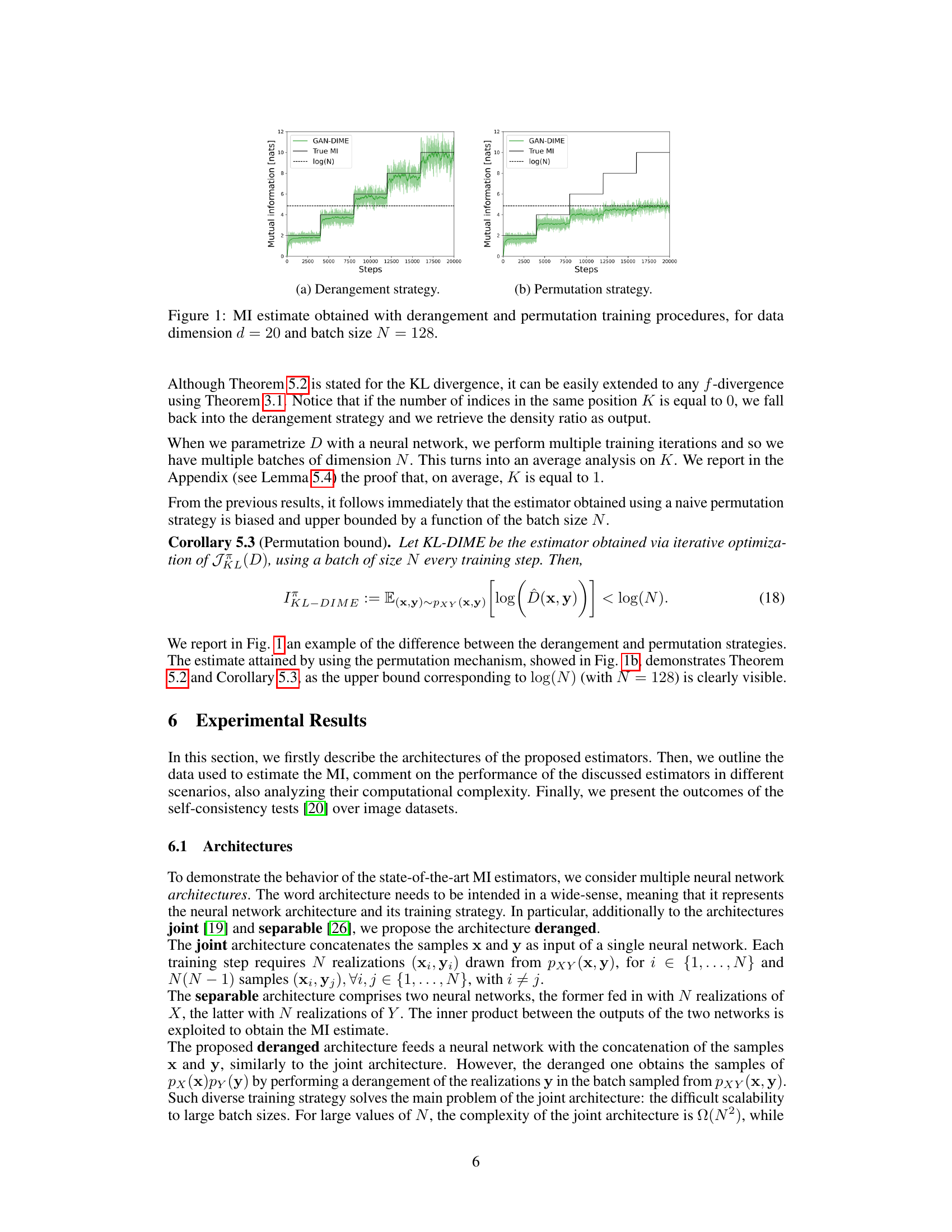
This figure compares the performance of MI estimation using two different training strategies: derangement and permutation. The x-axis represents the training steps, and the y-axis shows the estimated mutual information in nats. The solid black line indicates the true mutual information. The dashed black line represents the upper bound of log(N) for the permutation strategy. The green line shows the MI estimates obtained by using the derangement strategy, demonstrating its ability to overcome the upper bound. The shaded green area shows the variance of the estimates during training.

This table compares three different neural network architectures used for mutual information estimation: Joint, Separable, and Deranged. The ‘Input’ row shows the number and type of data pairs fed into the networks for training. ‘Nr. NNs’ indicates the number of neural networks used in each architecture. Finally, ‘Complexity’ shows the computational complexity in Big O notation, indicating how the computational time scales with the batch size (N).
In-depth insights#
f-DIME: A New Class#
The proposed heading “f-DIME: A New Class” hints at a novel contribution within the field of mutual information estimation. f-DIME likely refers to a new algorithm or framework, and the “f” likely suggests a reliance on f-divergences—a broad class of statistical distances— offering flexibility in estimator design. The phrase “New Class” implies a significant departure from existing methods, perhaps by introducing a fundamentally different approach to estimating mutual information, possibly leveraging the properties of various f-divergences for improved accuracy, robustness, or computational efficiency. The innovation may involve a new way to represent or approximate mutual information using f-divergences, resulting in estimators with superior bias-variance tradeoffs compared to prior techniques. This could entail new theoretical foundations, architectural designs for implementing the estimator, or advanced training methodologies. Overall, the “f-DIME: A New Class” heading suggests a significant advancement in the field with potentially wide-ranging implications for various applications relying on accurate mutual information estimation.
Derangement Training#
The proposed derangement training strategy is a crucial innovation in mutual information (MI) estimation. Standard approaches often shuffle data to create marginal samples, but this can lead to biased estimates because some pairs might remain unchanged, effectively still representing the joint distribution. Derangements, by definition, ensure that no data point remains in its original position, creating valid marginal samples. This novel technique directly addresses a significant limitation of previous discriminative MI estimators, thereby enhancing the accuracy and reliability of the method. The impact is particularly important in high-dimensional spaces where traditional methods struggle. Derangement training improves the bias/variance trade-off and thus yields more precise MI estimates. This is shown experimentally with lower variance compared to methods using random permutations. The effectiveness of this approach is a key contribution in improving the accuracy of discriminative MI estimation, especially in complex, high-dimensional datasets.
Variance Analysis#
A variance analysis in the context of mutual information estimation focuses on quantifying the uncertainty or variability inherent in the estimation process. High variance indicates that the estimates fluctuate significantly across different samples, making it challenging to reliably determine the true mutual information. The analysis would delve into the factors contributing to this variance, such as the sample size, dimensionality of the data, and the choice of estimation method. A key aspect often explored is the trade-off between bias and variance. Low variance estimators are desirable, but they might come at the cost of increased bias, meaning the estimator consistently under- or overestimates the true value. The analysis might compare the variance of different estimators, providing insights into their relative robustness and reliability across diverse scenarios. The results would highlight the importance of selecting an appropriate estimator, considering the characteristics of the data and the desired accuracy.
Experimental Results#
The heading ‘Experimental Results’ in a research paper warrants a thorough analysis. It should present a clear and concise overview of the experiments conducted, emphasizing the methods used, and providing a detailed account of the findings. The quality of this section hinges on the clarity of presentation, employing tables and figures effectively to support claims. Statistical significance must be meticulously addressed, including error bars and effect sizes, so readers can assess the robustness of the results. Crucially, the results section should directly address the hypotheses or research questions outlined in the paper’s introduction. A strong results section connects observations to the broader implications of the research. It should explicitly discuss limitations, acknowledging any unexpected findings or shortcomings, thus enhancing the overall credibility of the study. Finally, a comprehensive discussion comparing these results to prior work or benchmarks would highlight the significance and impact of the research.
Future Research#
Future research directions stemming from this mutual information estimation work could involve several key areas. Extending the f-DIME framework to encompass a broader range of f-divergences beyond those explored is crucial to understand the performance tradeoffs and identify optimal choices for diverse data characteristics. Investigating alternative architectural designs for the discriminator network, such as incorporating convolutional layers for image data or recurrent layers for sequential data, could significantly improve performance and scalability. A theoretical analysis of the derangement strategy’s convergence properties under various distributional assumptions would provide deeper understanding and possibly lead to more efficient sampling techniques. Finally, application of f-DIME to real-world problems in fields like biology, communications, or neuroscience, to demonstrate its practical utility in high-dimensional settings, is a vital next step.
More visual insights#
More on figures
This figure compares the performance of MI estimation using two different training strategies: derangement and permutation. The plots show the MI estimate over training steps for a 20-dimensional dataset with a batch size of 128. The derangement strategy consistently achieves better accuracy and avoids the upper bound limitations observed in the permutation strategy.
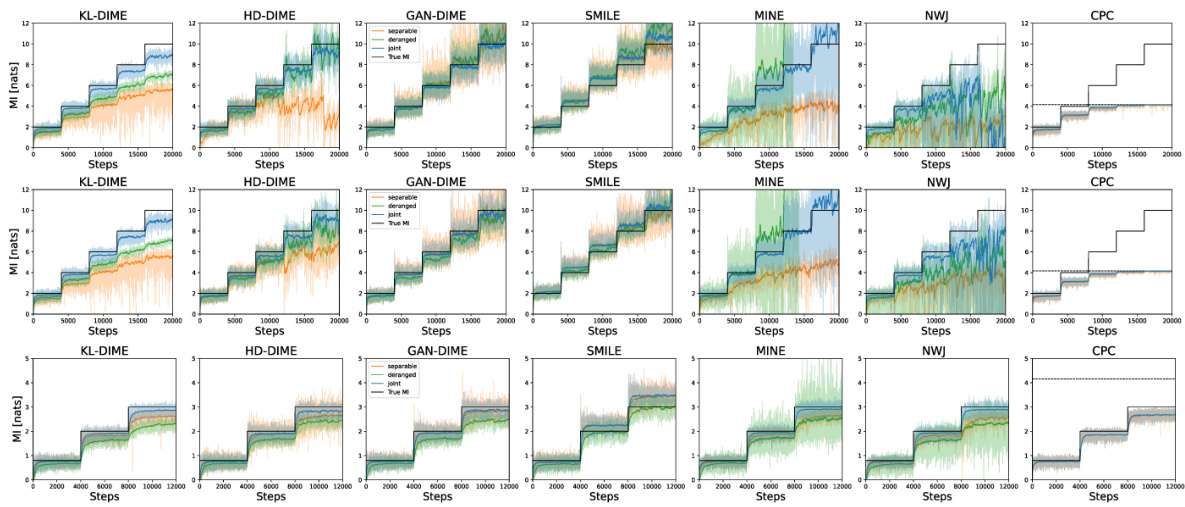
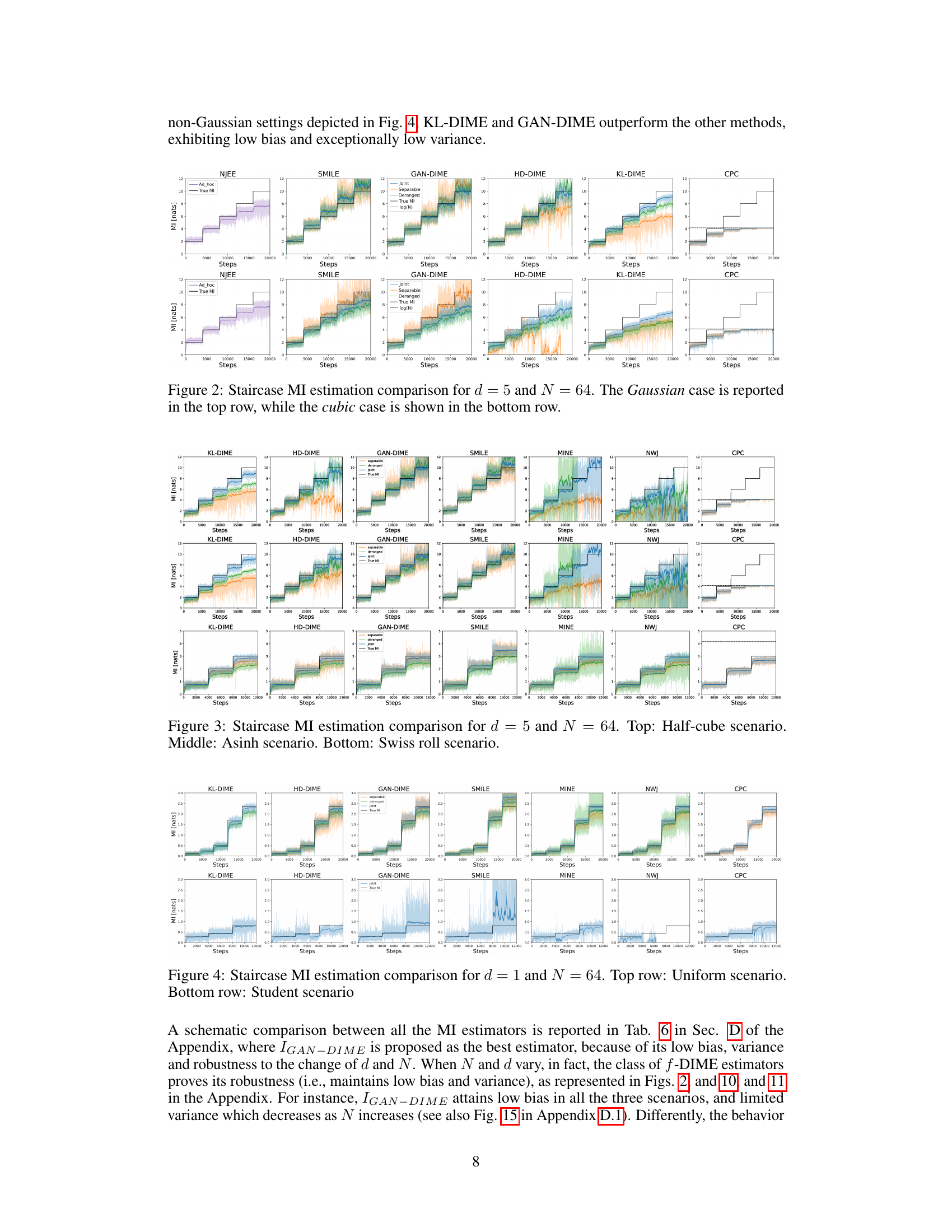
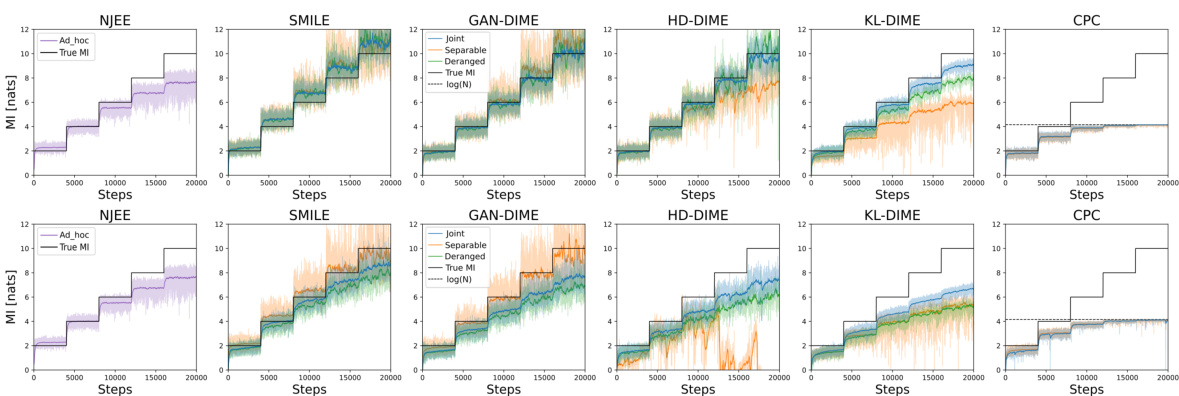
This figure compares the performance of three different mutual information (MI) estimation methods: NWJ, SMILE (with t = ∞), and MINE. The comparison is done across two different data settings: a Gaussian setting and a cubic setting. Each setting has varying levels of mutual information, visualized as a staircase pattern in the graphs. The x-axis represents the number of training steps, and the y-axis represents the estimated mutual information. The graphs show that the variance of the estimates increases significantly as the true mutual information increases, especially for MINE and NWJ.

This figure compares the performance of three different mutual information estimation methods (NWJ, SMILE, and MINE) under two different data distributions (Gaussian and cubic) for a dimensionality of 20 and batch size of 64. Each row shows the estimation for a specific data distribution across various true MI values. The plot shows the estimated MI on the y-axis and training steps on the x-axis, comparing the performance of each estimator with the true MI.

This figure shows the time taken for different MI estimation methods to complete a 5-step staircase Mutual Information estimation task. The three subplots demonstrate how the computation time scales with respect to three different parameters: (a) the batch size N, (b) the batch size N for the deranged and separable architectures, and (c) the dimension of the probability distribution d. The results highlight the efficiency of the deranged architecture compared to the joint and separable ones, especially when N is large.
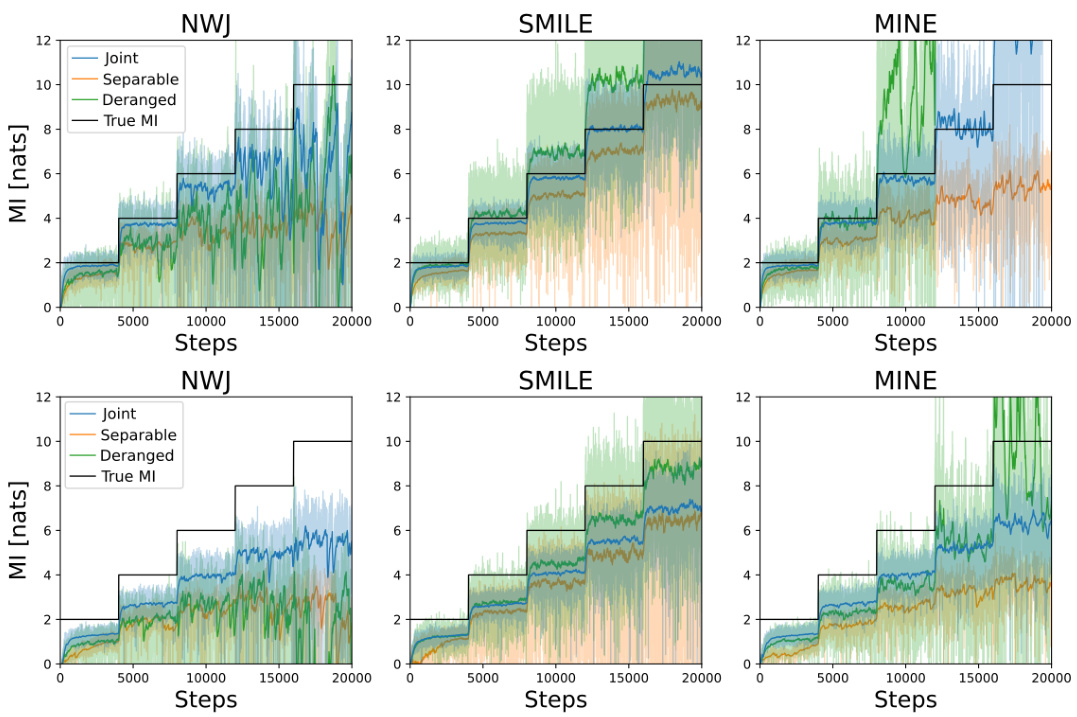
This figure compares the performance of three established mutual information (MI) estimation methods: NWJ, SMILE (with t = ∞), and MINE. The comparison is done across two scenarios: a Gaussian distribution and a cubic transformation of a Gaussian distribution. Each scenario is represented by two subfigures showing the estimated MI over training steps. The black lines depict the true MI value, highlighting the accuracy and variance of the different estimation methods. The Gaussian scenario exhibits relatively smoother MI estimates compared to the cubic scenario. This difference underscores the challenge in MI estimation for non-linear relationships.

This figure compares the performance of the MI estimation using two different training procedures: derangement and permutation. The derangement strategy ensures that samples from the marginal distribution do not include any samples from the joint distribution, overcoming the upper bound on the MI estimation. Conversely, the permutation strategy does not make this guarantee. The plot shows the mutual information estimates over training steps, demonstrating the derangement strategy’s clear advantage in achieving higher accuracy and avoiding a log(N) upper bound.
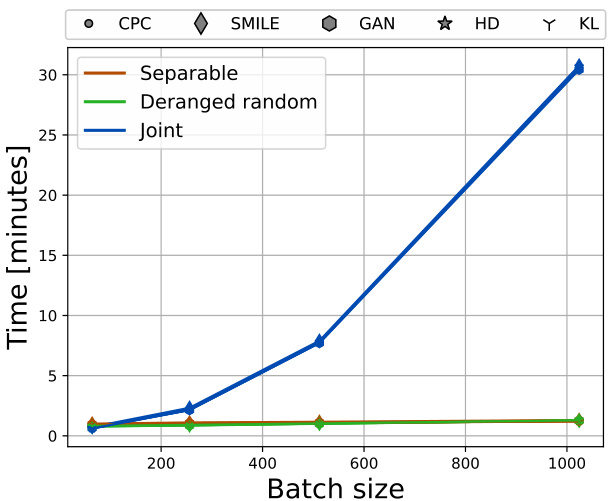
This figure shows the time taken to estimate mutual information (MI) using different methods and varying parameters. The left and center plots demonstrate how the computation time scales with increasing batch size (N) for different neural network architectures (Joint, Separable, Deranged). The right plot illustrates how the computation time changes as the dimension of the probability distribution (d) increases.

This figure shows how the variance of different f-DIME estimators changes with batch size for various values of mutual information (MI). The plot displays the variance on a logarithmic scale for each estimator (KL-DIME, HD-DIME, GAN-DIME, SMILE (tau=infty), MINE, and NWJ) across different MI levels (2, 4, 6, 8, 10 nats). It illustrates the variance performance of f-DIME compared to other existing MI estimators.
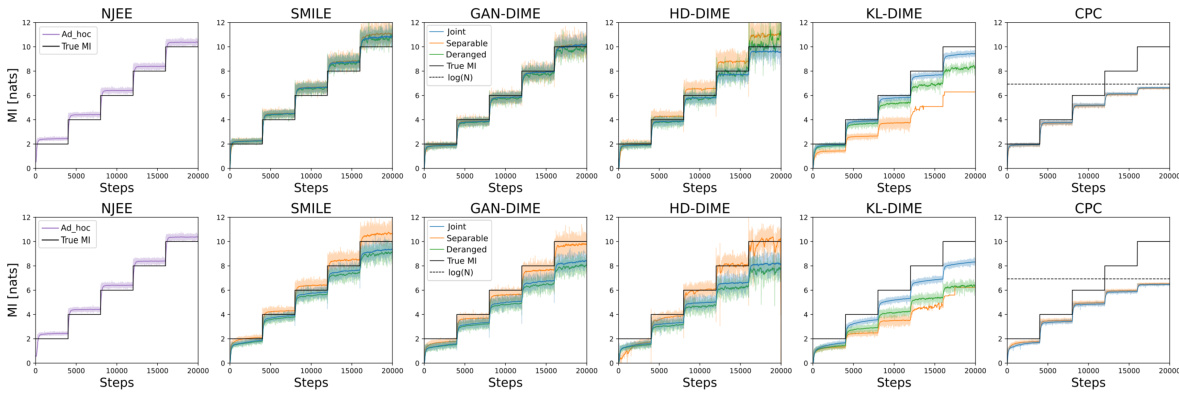
This figure compares the performance of the MI estimation using two different training strategies: derangement and permutation. The x-axis represents the number of training steps, and the y-axis shows the estimated mutual information in nats. The ‘True MI’ line indicates the actual mutual information value. The plot shows that the derangement strategy yields a more accurate and stable estimation of MI compared to the permutation strategy. The permutation strategy’s estimate is limited by log(N), highlighting a key advantage of the proposed derangement method.

This figure compares the MI estimation results using two different training strategies: derangement and permutation. The x-axis represents the number of training steps, and the y-axis shows the estimated mutual information (in nats). The black line represents the true MI value. The plots show that the derangement strategy yields a more accurate and stable estimation of MI, while the permutation strategy leads to a significantly biased estimate that is upper-bounded by log(N).
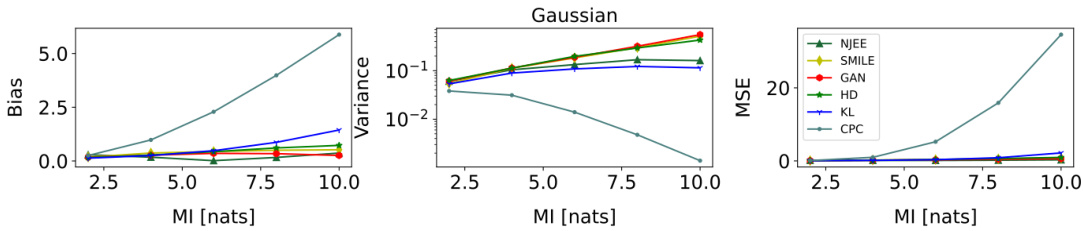
This figure shows how the variance of different f-DIME estimators changes with different batch sizes for various MI values. The x-axis represents the batch size, and the y-axis represents the variance. Different colors represent different f-divergences (KL, GAN, HD) used in the f-DIME estimators. The subplots are arranged by MI value, showing the variance for each estimator at different MI levels and batch sizes. The plot demonstrates the relationship between batch size and the variance of MI estimation, highlighting the impact of this factor on the performance of different f-DIME versions.
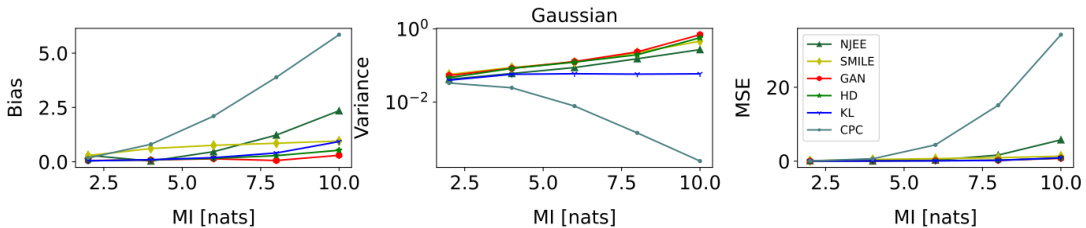
The figure shows how the variance of different f-DIME estimators changes with varying batch sizes for different mutual information (MI) values. Each subplot represents a different MI value (2, 4, 6, 8, 10 nats), and each line within a subplot represents a different f-divergence used in the estimator (KL, GAN, HD). The results demonstrate the impact of batch size on the variance, highlighting the relative performance of various f-divergences under different conditions. This is relevant for understanding how the choice of f-divergence and batch size impacts the accuracy and stability of MI estimation.
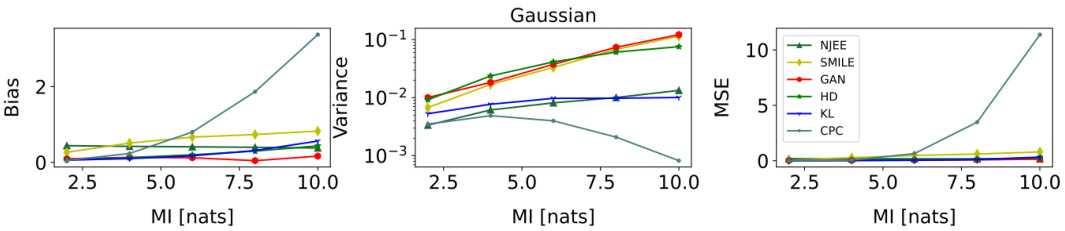
This figure shows how the variance of different f-DIME estimators changes with the batch size. Each subplot represents a different true mutual information (MI) value (2, 4, 6, 8, and 10 nats). Within each subplot, the variance of each estimator (KL-DIME, GAN-DIME, HD-DIME) is plotted against the batch size. This visualization helps illustrate the impact of batch size on the variance of the f-DIME estimators and allows for a comparison of the different estimators at various MI values.

This figure displays the variance of three f-DIME estimators (KL-DIME, GAN-DIME, and HD-DIME) across different batch sizes for various MI values (2, 4, 6, 8, and 10 nats). The plots illustrate how the variance changes as the batch size increases for each estimator and MI level. The results are particularly relevant to understanding the impact of batch size on the estimation accuracy of the proposed estimators.
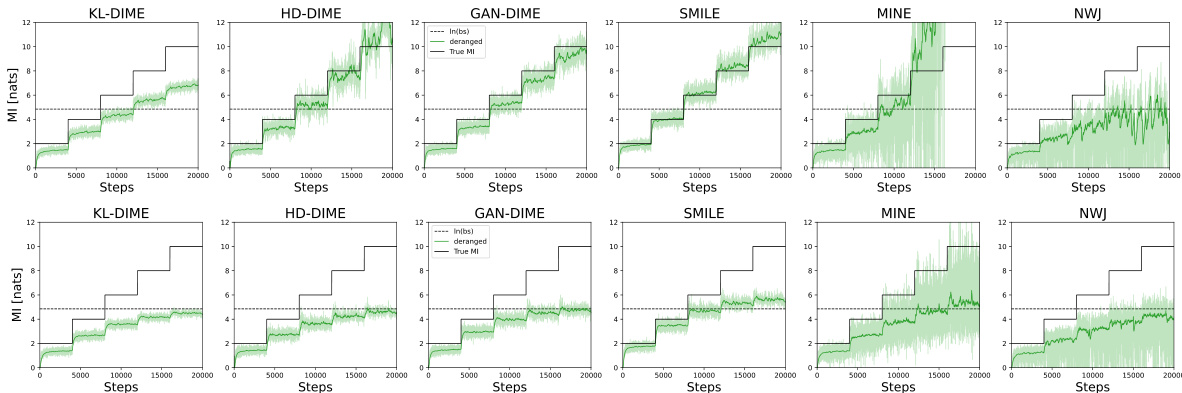
This figure compares the MI estimation results obtained using derangement and permutation training strategies. The x-axis represents the training steps, and the y-axis represents the estimated mutual information in nats. The plot shows that the derangement strategy converges to the true MI value more consistently than the permutation strategy, which appears to be upper-bounded by log(N).
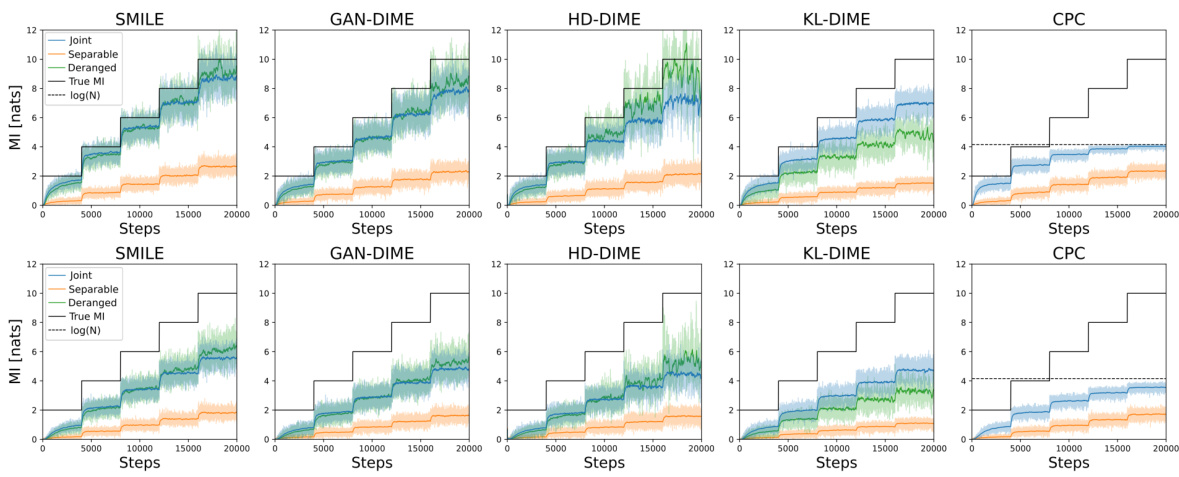
The figure compares the MI estimation performance of two training strategies: derangement and permutation. The x-axis represents the number of training steps, and the y-axis shows the estimated mutual information (MI) in nats. The derangement strategy consistently estimates MI more accurately than the permutation strategy, which is bounded by log(N) as demonstrated by the plot. This highlights the effectiveness of the proposed derangement strategy for accurate MI estimation.

This figure compares the performance of three mutual information (MI) estimation methods (NWJ, SMILE, and MINE) under two different data distributions: Gaussian and cubic. The plots show the MI estimates over training steps for different true MI values. The top row displays the results for Gaussian data, while the bottom row shows the results for cubic data. The comparison helps to visualize how well each method estimates MI under varying conditions and the impact of data distribution on estimation accuracy.
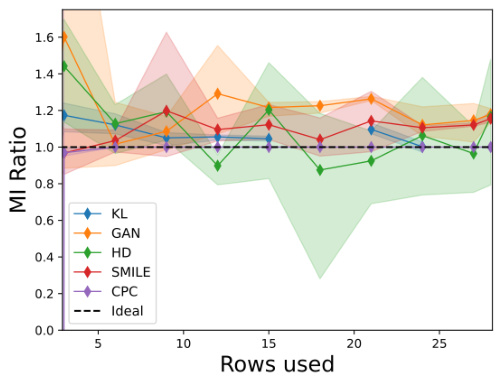
This figure shows the results of the baseline self-consistency test on MNIST and FashionMNIST datasets. The baseline test checks if the estimated mutual information (MI) between an image X and a masked version of the same image Y (where only the top t rows are visible) increases monotonically with t, starting from 0 (when X and Y are independent) and approaching 1 (when the mask is removed). The plot displays the MI ratio (MI(X; Y) / MI(X; X)) for different estimators (KL, GAN, HD, SMILE, CPC) across various values of t (number of rows used). The shaded areas represent the standard deviation, showing the variability of the estimates.

This figure shows the results of self-consistency tests for different MI estimators on MNIST and FashionMNIST datasets. The baseline property test checks if the estimated mutual information (MI) between an image X and its masked version Y (showing only the top t rows) is non-decreasing with t, starting from 0 and converging to 1 as t increases. The shaded area represents the variance across multiple runs.

This figure compares the performance of several Mutual Information (MI) estimators on the baseline property test. The baseline property assesses how well the estimators estimate the MI between an image and a masked version of the same image. The x-axis represents the number of rows used from the top of the image. The y-axis represents the MI ratio (estimated MI divided by the MI between the original image and itself). The ideal behavior would be a monotonically increasing function, starting from 0 and asymptotically approaching 1 as more rows are included. The shaded areas represent the variance of the estimates. Different colors represent different MI estimation methods. MNIST and FashionMNIST are two different image datasets used for this comparison.

This figure compares the performance of mutual information (MI) estimation using two different training strategies: derangement and permutation. The x-axis represents the number of training steps, and the y-axis shows the estimated MI in nats. The derangement strategy consistently provides a more accurate estimation of the true MI, while the permutation strategy’s estimations are bounded by log(N), demonstrating the significant benefit of using derangements.
More on tables

This table compares the variance of several mutual information (MI) estimation methods. It shows the variance for each method across different true MI values (2, 4, 6, 8, 10 nats). The methods compared include: NWJ, MINE, SMILE (with τ = ∞), GAN-DIME, HD-DIME, and KL-DIME. The joint architecture was used for all methods, with data dimensionality d=5 and batch size N=64. The table highlights the significantly lower variance achieved by the f-DIME estimators, especially at higher MI values, compared to traditional variational lower bound (VLB) methods like NWJ, MINE, and SMILE.

This table compares the variance of several mutual information estimators, including variations of the Variational Lower Bound (VLB) methods and the proposed f-DIME estimators, under specific conditions (dimension d=5 and sample size N=64). It highlights how the variance changes across different methods and mutual information values within the Gaussian setting, providing insights into the performance and stability of different MI estimation approaches.

This table compares the variance of several mutual information (MI) estimation methods. It shows the variance for different values of MI, using the joint neural network architecture with data dimensionality (d) of 5 and a batch size (N) of 64. The methods compared include NWJ, MINE, SMILE, GAN-DIME, HD-DIME, and KL-DIME. The table highlights the significantly lower variance of the f-DIME estimators compared to the traditional variational lower bound (VLB) methods (NWJ, MINE, SMILE).
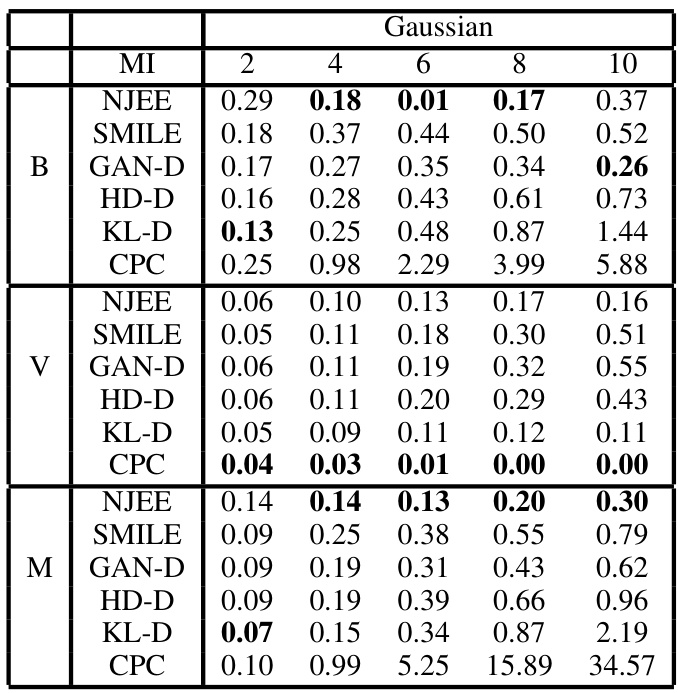
This table compares the variance of several mutual information (MI) estimation methods. It shows the variance for different values of the true MI, using the joint neural network architecture with data dimensionality (d) of 5 and batch size (N) of 64 for a Gaussian data distribution. The methods compared include several variational lower bound (VLB) based estimators (NWJ, MINE, SMILE) and the proposed f-DIME estimators (GAN-DIME, HD-DIME, KL-DIME). The table highlights the lower variance achieved by the f-DIME estimators compared to the VLB methods.
Full paper#